群

在數學中，群（英語：group）是指配備二元運算的集合，其二元運算需要具有結合律、單位元和反元素。因為眾多數學結構都是群（如整數系配備上加法就形成一個群），因而可以簡潔地從不同的數學結構歸納出共通的結果，這使群成為當代數學的核心概念。^[1][2]

關於與「群」標題相近或相同的條目，請見「群 (消歧義)」。

此條目介紹的是基本概念。關於進階的主題，請見「群論」。

扭計骰的所有可能重新排列形成一個群，叫做扭計骰群。

群論
群
基本概念 子群 · 正規子群 · 商群 · 群同態 · 像 · (半)直積 · 直和 單純群 · 有限群 · 無限群 · 拓撲群 · 群概形 · 循環群 · 冪零群 · 可解群 · 圈積 離散群 有限單群分類 循環群 Zn 交錯群 An 李型群 散在群 馬蒂厄群 M11..12,M22..24 康威群 Co1..3 揚科群 J1..4 費歇爾群（英語：Fischer group）F22..24 子魔群（英語：sub monster group） B 魔群 M 其他有限群 對稱群, Sn 二面體群, Dn 無限群 整數, Z 模群, PSL(2,Z) 和 SL(2,Z) 連續群 李群 一般線性群 GL(n) 特殊線性群 SL(n) 正交群 O(n) 特殊正交群 SO(n) 么正群 U(n) 特殊么正群 SU(n) 辛群 Sp(n) G2 F4 E6 E7 E8 勞侖茲群 龐加萊群 無限維群 共形群 微分同胚群 環路群 量子群 O(∞) SU(∞) Sp(∞) 代數群 橢圓曲線 線性代數群（英語：Linear algebraic group） 阿貝爾簇（英語：Abelian variety）
閱 論 編

很多自然界的變換（如平移、鏡射）的匯總都符合群的定義，而某群變換下保持不變的某種性質被稱為對稱性；如在空間對稱群的哪些變換下，面積或角度會保持不變，就是在研究立體幾何的對稱性。

歷史

主條目：群論的歷史

抽象群的現代概念是從多個數學領域發展出來的。^[3][4][5]群論的最初動機是為了求解高於4次的多項式方程。十九世紀法國數學家埃瓦里斯特·伽羅瓦，擴展了保羅·魯菲尼和約瑟夫·拉格朗日先前的工作，依據特定多項式方程的根（解）的對稱群給出了對它的可解性的判別準則。這個伽羅瓦群的元素對應於根的特定置換。伽羅瓦的想法最初被同代人所拒絕，只在死後才出版。^[6][7]更一般的置換群由奧古斯丁·路易·柯西專門研究。阿瑟·凱萊的「On the theory of groups, as depending on the symbolic equation ${\displaystyle \vartheta ^{n}=1}$」（1854 年）給出有限群的第一個抽象定義。^[8]

幾何是第二個系統性的使用群，特別是對稱群的領域。這類群是菲利克斯·克萊因 1872 年的愛爾蘭根綱領的一部分。^[9]在新型的幾何如雙曲幾何和射影幾何形成之後，克萊因利用群論以更連貫的方式來組織它們。索菲斯·李進一步發展了這些想法，在 1884 年創立了李群的研究。^[10]

對群論有貢獻的第三個領域是數論。一些阿貝爾群結構在卡爾·弗里德里希·高斯的數論著作《算術研究》（1798 年）中被隱含地用到，並被利奧波德·克羅內克更明顯地用到。^[11] 1847 年，恩斯特·庫默爾發展了描述用質數做因數分解的理想類群，使證明費馬大定理的早期嘗試達到了高潮。^[12]

把上述各種來源融合成一個群的統一理論是從卡米爾·若爾當的「Traité des substitutions et des équations algébriques」 (1870 年）開始的。^[13] 瓦爾特·馮·迪克（1882年）給出了第一個抽象群的現代定義的陳述。^[14]在二十世紀，群在費迪南德·格奧爾格·弗比尼斯和威廉·伯恩賽德的開拓性著作中獲得了廣泛的認識，他們研究有限群的表示理論，還有理查德·布勞爾的模表示論和 Issai Schur 的論文。^[15] 赫爾曼·外爾、埃利·嘉當和很多其他人推進了李群和更一般的局部緊群的理論。^[16]它的代數對應者——代數群的理論，由克勞德·舍瓦萊（從 1930 年代晚期開始）和後來阿爾曼德·波萊爾和雅克·蒂茨的重要著作奠基。^[17]

芝加哥大學於 1960-61 年舉辦的「群論年」活動促使群論家們以丹尼爾·戈倫斯坦，約翰·格里格斯·湯普森和瓦爾特·法伊特為基礎展開合作。在大量其他數學家的幫助下，他們完成了有限單純群的分類。這項工程，不論是從證明長度來說還是從參與人數來說，其浩大程度超越了之前一切的數學成果。簡化此證明的研究還在進行中。^[18]群論在當下仍是一個活躍的數學分支，並仍在對其他分支產生重大影響。^[a]

正式定義

給定集合 ${\displaystyle G}$ ，且它配備的二元運算 ${\displaystyle \circ :G\times G\to G}$ 滿足（其中運算結果 ${\displaystyle \circ (a,\,b)}$ 被簡記為 ${\displaystyle a\circ b}$ ）：^[19]

結合律	對所有 ${\displaystyle g_{1},\,g_{2},\,g_{3}\in G}$ 有 ${\displaystyle g_{1}\circ (g_{2}\circ g_{3})=(g_{1}\circ g_{2})\circ g_{3}}$
左單位元與左反元素	存在 ${\displaystyle e\in G}$ ，對所有 ${\displaystyle g\in G}$ 有	${\displaystyle e\circ g=g}$
		且存在 ${\displaystyle \gamma \in G}$ 使得 ${\displaystyle \gamma \circ g=e}$

的話，稱 ${\displaystyle (G,\ \circ )}$ 是一個群。當其配備的二元運算 ${\displaystyle \circ }$ 不是那麼重要時， ${\displaystyle (G,\ \circ )}$ 也常常簡記為 ${\displaystyle G}$。單位元常稱作單位元。

群運算的次序很重要，也就是說，等式 ${\displaystyle a\circ b=b\circ a}$（交換律）不一定成立。滿足交換律的群稱為交換群（或阿貝爾群，以尼爾斯·阿貝爾命名），不滿足交換律的群稱為非交換群（非阿貝爾群）。如以下面舉例一節的二面體群就不是交換群。

等價的定義

上面關於單位元和反元素的部分也可以改為：

右單位元與右反元素	存在 ${\displaystyle e\in G}$ ，對所有 ${\displaystyle g\in G}$ 有	${\displaystyle g\circ e=g}$
		且存在 ${\displaystyle \gamma \in G}$ 使得 ${\displaystyle g\circ \gamma =e}$

因為不管原來的淡紫色定義，還是淡黃色的替代性定義，配上結合律都會等價於以下的定義：

單位元與反元素	存在 ${\displaystyle e\in G}$ ，對所有 ${\displaystyle g\in G}$ 有	${\displaystyle e\circ g=g\circ e=g}$
		且存在 ${\displaystyle \gamma \in G}$ 使得 ${\displaystyle \gamma \circ g=g\circ \gamma =e}$

證明

若二元運算 ${\displaystyle \circ :G\times G\to G}$ 滿足結合律，且 ${\displaystyle e_{l}\in G}$ 對任意 ${\displaystyle g\in G}$ 有

「${\displaystyle e_{l}\circ g=g}$ 」(left-1)

「存在某 ${\displaystyle \gamma _{l}\in G}$ 使 ${\displaystyle \gamma _{l}\circ g=e_{l}}$」(left-2)

因為 ${\displaystyle \circ }$ 是二元運算， ${\displaystyle g\circ \gamma \in G}$ 。所以根據 (left-2)，存在 ${\displaystyle \Gamma \in G}$ 滿足

${\displaystyle \Gamma \circ (g\circ \gamma _{l})=e_{l}}$

這樣根據結合律和 (left-1) 與 (left-2) 有

${\displaystyle {\begin{aligned}e_{l}&=\Gamma \circ (g\circ \gamma _{l})\\&=\Gamma \circ [\,g\circ (e_{l}\circ \gamma _{l})\,]\\&=\Gamma \circ \{\,g\circ [\,(\gamma _{l}\circ g)\circ \gamma _{l}\,]\,\}\\&=\Gamma \circ \{\,g\circ [\,\gamma _{l}\circ (g\circ \gamma _{l})\,]\,\}\\&=\Gamma \circ [\,(g\circ \gamma _{l})\circ (g\circ \gamma _{l})\,]\\&=[\,\Gamma \circ (g\circ \gamma _{l})\,]\circ (g\circ \gamma _{l})\\&=e_{l}\circ (g\circ \gamma _{l})\\&=g\circ \gamma _{l}\end{aligned}}}$

所以左反元素必為右反元素，這樣根據結合律有

${\displaystyle {\begin{aligned}g\circ e_{l}&=g\circ (\gamma _{l}\circ g)\\&=(g\circ \gamma _{l})\circ g\\&=e_{l}\circ g=g\end{aligned}}}$

所以左單位元必為右單位元。

類似地，若二元運算 ${\displaystyle \circ :G\times G\to G}$ 滿足結合律，且 ${\displaystyle e_{r}\in G}$ 對所有 ${\displaystyle g\in G}$ 有

「 ${\displaystyle g\circ e_{r}=g}$ 」(right-1)

「存在某 ${\displaystyle \gamma _{r}\in G}$ ，使 ${\displaystyle g\circ \gamma _{r}=e_{r}}$ 」(right-2)

因為 ${\displaystyle \gamma _{r}\circ g\in G}$ ，所以根據 (right-2) 存在 ${\displaystyle {\overline {\Gamma }}\in G}$ 滿足

${\displaystyle (\gamma _{r}\circ g)\circ {\overline {\Gamma }}=e_{r}}$

所以根據結合律、(right-1) 和 (right-2) 有

${\displaystyle {\begin{aligned}e_{r}&=(\gamma _{r}\circ g)\circ {\overline {\Gamma }}\\&=[\,(\gamma _{r}\circ e_{r})\circ g\,]\circ {\overline {\Gamma }}\\&=\{\,[\,\gamma _{r}\circ (g\circ \gamma _{r})\,]\circ g\,\}\circ {\overline {\Gamma }}\\&=\{\,[\,(\gamma _{r}\circ g)\circ \gamma _{r}\,]\circ g\,\}\circ {\overline {\Gamma }}\\&=[\,(\gamma _{r}\circ g)\circ (\gamma _{r}\circ g)\,]\circ {\overline {\Gamma }}\\&=(\gamma _{r}\circ g)\circ [\,(\gamma _{r}\circ g)\circ {\overline {\Gamma }}\,]\\&=(\gamma _{r}\circ g)\circ e_{r}\\&=\gamma _{r}\circ g\end{aligned}}}$

所以右反元素也為左反元素。這樣根據結合律有

${\displaystyle {\begin{aligned}e_{r}\circ g&=(g\circ \gamma _{r})\circ g\\&=g\circ (\gamma _{r}\circ g)\\&=g\circ e_{r}=g\end{aligned}}}$

所以右單位元必為左單位元。

再考慮到淡藍色是要求 ${\displaystyle e\in G}$ 同時為左右單位元且存在左右反元素，這樣就證明以上三種定義在有結合律的前提下等價。

舉例

整數加法群

整數系 ${\displaystyle \mathbb {Z} }$ 是由所有整數所組成：

${\displaystyle \dots ,\,-4,\,-3,\,-2,\,-1,\,0,\,1,\,2,\,3,\,4,\dots }$^[20]

可以看出，整數系和整數的加法是可以構成群的：

1. 對於任意兩個整數 ${\displaystyle a}$ 和 ${\displaystyle b}$，它們的和 ${\displaystyle a+b}$ 也是整數，所以整數加法的確是個二元運算，換言之，滿足封閉性。
2. 對於任意三個整數 ${\displaystyle a,\,b,\,c}$，有 ${\displaystyle (a+b)+c=a+(b+c)}$。也就是說，先把 ${\displaystyle a}$ 加到 ${\displaystyle b}$，然後把它們的和加到 ${\displaystyle c}$，所得到的結果與把 ${\displaystyle a}$ 加到 ${\displaystyle b}$ 與 ${\displaystyle c}$ 的和是相等的。
3. 對於任意整數 ${\displaystyle a}$，有 ${\displaystyle a+0=0+a=a}$。故而 ${\displaystyle 0}$ 是整數加法的單位元。同時，對所有整數 ${\displaystyle a}$，均存在與之對應的另一個整數 ${\displaystyle -a}$，滿足 ${\displaystyle a+(-a)=(-a)+a=0}$，作爲 ${\displaystyle a}$ 的反元素。

實數乘法群

實數集去掉 ${\displaystyle 0}$，即 ${\displaystyle \mathbb {R} ^{\sharp }:=\mathbb {R} \backslash \{0\}}$，在實數乘法下構成群，驗證如下：

1. ${\displaystyle \forall a,\,b\in \mathbb {R} ^{\sharp },\,ab\in \mathbb {R} ^{\sharp }}$;
2. ${\displaystyle \forall a,\,b,\,c\in \mathbb {R} ^{\sharp },\,(ab)c=a(bc)}$;
3. 對於 ${\displaystyle 1\in \mathbb {R} ^{\sharp }}$, ${\displaystyle \forall a\in \mathbb {R} ^{\sharp },\,a1=1a=a}$;
4. ${\displaystyle \forall a\in \mathbb {R} ^{\sharp },\,\exists a^{-1}\in \mathbb {R} ^{\sharp },\,a\left(a^{-1}\right)=\left(a^{-1}\right)a=1}$.

二面體群

主條目：二面體群

以下是正方形的 8 個旋轉和翻轉：

${\displaystyle \operatorname {id} }$ (保持原樣)	${\displaystyle r_{1}}$ (向右旋轉 90°)	${\displaystyle r_{2}}$ (向右旋轉 180°)	${\displaystyle r_{3}}$（向右旋轉 270°）
${\displaystyle f_{v}}$ (垂直翻轉)	${\displaystyle f_{h}}$ (水平翻轉)	${\displaystyle f_{d}}$ (對角翻轉)	${\displaystyle f_{c}}$（反對角翻轉）
注意顏色不同，「操作結果」才不同。數字只是去方便理解「操作過程」，數字有沒有顛倒不影響「操作結果」。

如果 ${\displaystyle a}$ 和 ${\displaystyle b}$ 是上述 8 個「操作」的其中一個，「操作的複合」 ${\displaystyle a\circ b}$ 定義為先對正方形操作 ${\displaystyle a}$ 之後再操作 ${\displaystyle b}$ 。比如說，右旋 270° ( ${\displaystyle r_{3}}$ ) 然後水平翻轉（ ${\displaystyle f_{h}}$ ），等同於沿對角線的反射（ ${\displaystyle f_{d}}$ ），這樣就可以表示為 ${\displaystyle r_{3}\circ f_{h}=f_{d}}$ 。

下面的群表列出了這種「操作的複合」的所有可能結果。

${\displaystyle \circ }$		先操作
		${\displaystyle \operatorname {id} }$	${\displaystyle r_{1}}$	${\displaystyle r_{2}}$	${\displaystyle r_{3}}$	${\displaystyle f_{v}}$	${\displaystyle f_{h}}$	${\displaystyle f_{d}}$	${\displaystyle f_{c}}$
後操作	${\displaystyle \operatorname {id} }$	${\displaystyle \operatorname {id} }$	${\displaystyle r_{1}}$	${\displaystyle r_{2}}$	${\displaystyle r_{3}}$	${\displaystyle f_{v}}$	${\displaystyle f_{h}}$	${\displaystyle f_{d}}$	${\displaystyle f_{c}}$
	${\displaystyle r_{1}}$	${\displaystyle r_{1}}$	${\displaystyle r_{2}}$	${\displaystyle r_{3}}$	${\displaystyle \operatorname {id} }$	${\displaystyle f_{c}}$	${\displaystyle f_{d}}$	${\displaystyle f_{v}}$	${\displaystyle f_{h}}$
	${\displaystyle r_{2}}$	${\displaystyle r_{2}}$	${\displaystyle r_{3}}$	${\displaystyle \operatorname {id} }$	${\displaystyle r_{1}}$	${\displaystyle f_{h}}$	${\displaystyle f_{v}}$	${\displaystyle f_{c}}$	${\displaystyle f_{d}}$
	${\displaystyle r_{3}}$	${\displaystyle r_{3}}$	${\displaystyle \operatorname {id} }$	${\displaystyle r_{1}}$	${\displaystyle r_{2}}$	${\displaystyle f_{d}}$	${\displaystyle f_{c}}$	${\displaystyle f_{h}}$	${\displaystyle f_{v}}$
	${\displaystyle f_{v}}$	${\displaystyle f_{v}}$	${\displaystyle f_{d}}$	${\displaystyle f_{h}}$	${\displaystyle f_{c}}$	${\displaystyle \operatorname {id} }$	${\displaystyle r_{2}}$	${\displaystyle r_{1}}$	${\displaystyle r_{3}}$
	${\displaystyle f_{h}}$	${\displaystyle f_{h}}$	${\displaystyle f_{c}}$	${\displaystyle f_{v}}$	${\displaystyle f_{d}}$	${\displaystyle r_{2}}$	${\displaystyle \operatorname {id} }$	${\displaystyle r_{3}}$	${\displaystyle r_{1}}$
	${\displaystyle f_{d}}$	${\displaystyle f_{d}}$	${\displaystyle f_{h}}$	${\displaystyle f_{c}}$	${\displaystyle f_{v}}$	${\displaystyle r_{3}}$	${\displaystyle r_{1}}$	${\displaystyle \operatorname {id} }$	${\displaystyle r_{2}}$
	${\displaystyle f_{c}}$	${\displaystyle f_{c}}$	${\displaystyle f_{v}}$	${\displaystyle f_{d}}$	${\displaystyle f_{h}}$	${\displaystyle r_{1}}$	${\displaystyle r_{3}}$	${\displaystyle r_{2}}$	${\displaystyle \operatorname {id} }$

如果取

${\displaystyle D_{4}=\left\{\operatorname {id} ,\,\,r_{1},\,r_{2},\,r_{3},\,f_{v},\,f_{h},\,f_{d},\,f_{c}\right\}}$，

那麼根據以上的群表， ${\displaystyle \circ :D_{4}\times D_{4}\to D_{4}}$ 的確是個二元運算，而且 ${\displaystyle (D_{4},\,\circ )}$ 為群（其中 ${\displaystyle \operatorname {id} }$ 符合單位元的要求），它被稱為二面體群。注意到上表淡紫色的部分破壞了交換律，所以二面體群不是交換群。

基本性質

主條目：初等群論

單位元的唯一性

若群 ${\displaystyle \left(G,\,\circ \right)}$ 同時有兩個單位元 ${\displaystyle e\in G}$ 和 ${\displaystyle e^{\prime }\in G}$ ，那根據定義裏對單位元的定義，對於任意 ${\displaystyle g\in G}$ 有：

${\displaystyle g=e\circ g=g\circ e}$

${\displaystyle g=e^{\prime }\circ g=g\circ e^{\prime }}$

這樣的話，把 ${\displaystyle g}$ 分別代換為 ${\displaystyle e^{\prime }}$ 和 ${\displaystyle e}$ 就有

${\displaystyle e^{\prime }=e\circ e^{\prime }=e^{\prime }\circ e}$

${\displaystyle e=e^{\prime }\circ e=e\circ e^{\prime }}$

所以

${\displaystyle e^{\prime }=e}$

所以群的單位元是唯一的，這樣根據函數符號與唯一性間的關係，可以添加新的三元函數符號 ${\displaystyle e_{(G,\,\circ )}}$ 與以下的新公理（以下的合式公式 ${\displaystyle {\mathcal {B}}}$ 是 「${\displaystyle \circ }$ 是 ${\displaystyle G}$ 上的一個二元運算，且存在 ${\displaystyle \circ }$ 的單位元」的正式邏輯表述）

${\displaystyle [\neg {\mathcal {B}}\wedge (e_{(G,\,\circ )}=\varnothing )]\vee [{\mathcal {B}}\wedge (\forall g\in G)(e_{(G,\,\circ )}\circ g=g\circ e_{(G,\,\circ )}=g)]}$

這條公理直觀上表示，只要「${\displaystyle \circ }$ 是 ${\displaystyle G}$ 上的一個二元運算，且存在 ${\displaystyle \circ }$ 的單位元」，就可以用 ${\displaystyle e_{(G,\,\circ )}}$ 這個符號簡記 「${\displaystyle \left(G,\,\circ \right)}$ 上的那個唯一單位元」，否則取 ${\displaystyle e_{(G,\,\circ )}}$ 為空集。

為了簡便起見， ${\displaystyle e_{(G,\,\circ )}}$ 通常記為 ${\displaystyle e_{G}}$ 甚至是 ${\displaystyle e}$ 。

反元素的唯一性

在增添以上的新函數符號 ${\displaystyle e_{(G,\,\circ )}}$ 和新公理的情況下，就可以證明反元素的唯一性。

若群 ${\displaystyle \left(G,\,\circ \right)}$ 的某元素 ${\displaystyle g\in G}$ 有兩個反元素 ${\displaystyle \gamma \in G}$ 和 ${\displaystyle {\bar {\gamma }}\in G}$ ，那根據定義和 ${\displaystyle e_{(G,\,\circ )}}$ 的新公理有

${\displaystyle e_{G}=g\circ \gamma =\gamma \circ g}$

${\displaystyle e_{G}=g\circ \gamma ^{\prime }=\gamma ^{\prime }\circ g}$

那這樣的話，依據定義裏的結合律和 ${\displaystyle e_{(G,\,\circ )}}$ 的新公理有

${\displaystyle {\begin{aligned}{\bar {\gamma }}&={\bar {\gamma }}\circ e_{G}\\&={\bar {\gamma }}\circ (g\circ \gamma )\\&=({\bar {\gamma }}\circ g)\circ \gamma \\&=e_{G}\circ \gamma \\&=\gamma \end{aligned}}}$

所以任意 ${\displaystyle g\in G}$ 只有一個反元素。這樣根據函數符號與唯一性間的關係，可以添加一個三元函數符號 ${\displaystyle {g^{-1}}_{(G,\,\circ )}}$ 與以下的新公理（以下的合式公式 ${\displaystyle {\mathcal {D}}}$ 是 「 ${\displaystyle \left(G,\,\circ \right)}$ 為一群，且 ${\displaystyle g\in G}$ 」的正式邏輯表述）

${\displaystyle [\neg {\mathcal {D}}\wedge ({g^{-1}}_{(G,\,\circ )}=\varnothing )]\vee [{\mathcal {D}}\wedge ({g^{-1}}_{(G,\,\circ )}\circ g={g^{-1}}_{(G,\,\circ )}\circ g=e_{G})]}$

這條公理直觀上表示，只要「${\displaystyle \left(G,\,\circ \right)}$ 為一群，且 ${\displaystyle g\in G}$」，就可以用 ${\displaystyle {g^{-1}}_{(G,\,\circ )}}$ 簡記 「${\displaystyle g}$ 在 ${\displaystyle \left(G,\,\circ \right)}$ 上對應的那個唯一反元素」，否則取 ${\displaystyle {g^{-1}}_{(G,\,\circ )}}$ 為空集。

簡便起見， ${\displaystyle {g^{-1}}_{(G,\,\circ )}}$ 通常記為 ${\displaystyle g^{-1}}$。

群的冪

若 ${\displaystyle \left(G,\,\circ \right)}$ 為一群，可以仿造整數指數，對任意 ${\displaystyle g\in G}$ 作如下關於符號簡寫的遞歸定義

${\displaystyle g^{0}:=e}$ （單位元視為 ${\displaystyle 0}$ 次方）

${\displaystyle g^{1}:=g}$

對所有的整數 ${\displaystyle n\in \mathbb {Z} }$ ， ${\displaystyle g^{n+1}:=g^{n}\circ g}$

對所有的整數 ${\displaystyle n\in \mathbb {Z} }$ ， ${\displaystyle g^{n-1}:=g^{n}\circ g^{-1}}$

除法與減法

有時，某個群的運算可以跟直觀上的加法聯想在一起，這個運算也可以改記為「 ${\displaystyle +}$ 」或「 ${\displaystyle \oplus }$ 」，這時也會把 ${\displaystyle f+g^{-1}}$ 改記為 ${\displaystyle f-g}$ 或 ${\displaystyle f\ominus g}$ ，這時會暱稱 ${\displaystyle f-g}$ 為減法。更有甚者，${\displaystyle g^{-1}}$ 會被記為 ${\displaystyle -g}$ 。

類似的，如果群的運算可以跟直觀上的乘法聯想在一起而改記為「 ${\displaystyle \times }$ 」或「 ${\displaystyle \otimes }$ 」，這時會把 ${\displaystyle f\times g^{-1}}$ 改記為 ${\displaystyle f\div g}$ 或 ${\displaystyle {\frac {f}{g}}}$ ，並暱稱為除法；更有甚者，${\displaystyle g^{-1}}$ 會被記為 ${\displaystyle {\frac {1}{g}}}$ 。

注意以上都是為了直觀理解方便所規定的簡寫，並不是斷定群的運算必然跟一般實數的加減乘除一模一樣。

群論術語

本章節羅列一些群論涉及到的概念，其並非群本身的固有性質，但其與群的應用息息相關。本章節使用了數學符號如 ${\displaystyle X=\{x,\,y,\,z\}}$ 以示集合 ${\displaystyle X}$ 包含元素 ${\displaystyle x,\,y}$ 和 ${\displaystyle z}$，或以 ${\displaystyle x\in X}$ 表記 ${\displaystyle x}$ 是 ${\displaystyle X}$ 的一個元素，而記號 ${\displaystyle f\colon ,\,X\to Y}$ 意指 ${\displaystyle f}$ 為將 ${\displaystyle X}$ 的所有元各自唯一指定到 ${\displaystyle Y}$ 的某個元的函數。

要超越上述純粹符號操作水平去理解群，必須採用更加結構性的概念。^[c]有一個概念性原理位於所有下列概念的底層：要發揮群提供的結構（而無結構的集合就沒有）的優勢，與群有關的構造必須與群運算兼容。下列概念中以各種方式表現了這種兼容性。例如，群可以通過叫做群同態的函數相互關聯。根據上述這個原理，要求它們以精確的意義照顧到群結構。群的結構還可以通過把它們分解成子群和商群來理解。「保持結構」的原理是在數學中反復出現的一個主題，它是靠範疇來工作的一個實例，在這裏的情況下靠群范疇。^[21]

群同態

主條目：群同態

群同態^[g]是保持群結構的映射。稱兩群之間的映射 ${\displaystyle \varphi \colon \,G\to H}$ 為群同態，當且僅當

${\displaystyle \varphi (a\circ _{G}b)=\varphi (a)\circ _{H}\varphi (b)}$

對 ${\displaystyle G}$ 的所有元 ${\displaystyle a,\,b}$ 均成立。上式同樣蘊含了 ${\displaystyle \varphi (e_{G})=e_{H}}$ 與 ${\displaystyle \forall a\in G,\,\varphi (a^{-1})=\left[\varphi (a)\right]^{-1}}$。因此說：群同態保持了群的所有結構。^[22]

兩群 ${\displaystyle G,\,H}$ 被稱作同構的，當且僅當存在群同態 ${\displaystyle \rho \colon \,G\to H,\,\sigma \colon \,H\to G}$，使得 ${\displaystyle \rho \sigma =\operatorname {id} _{G},\,\sigma \rho =\operatorname {id} _{H}}$，也就是説，其複合分別得到了 ${\displaystyle G}$ 和 ${\displaystyle H}$ 上的恆等變換，此時也記 ${\displaystyle \sigma =\varphi ^{-1}}$。從抽象的觀點來看，同構的一類群攜帶了完全相同的資訊，或者說，在「模去」群結構以外的性質後，所有同構的群可以視作唯一的單個對象。例如，對群 ${\displaystyle G}$ 中的某個元 ${\displaystyle a}$ 已經證實了 ${\displaystyle aa=e_{G}}$，如果另一群 ${\displaystyle H}$ 由映射 ${\displaystyle \varphi }$ 同構於該群，則相當於證明了 ${\displaystyle \varphi (a)\varphi (a)=\varphi (e_{G})=e_{H}}$。

此外，一個群可以擁有非恆等變換的自同態或自同構，如果以映射為元，映射複合為群乘法，則任意群 ${\displaystyle G}$ 擁有其自同態群和自同構群，分別記作 ${\displaystyle \operatorname {End} G}$ 和 ${\displaystyle \operatorname {Aut} G}$。

子群

主條目：子群

非正式地說，子群是包含在更大的群內的一個群。^[23]

具體而論，對群 ${\displaystyle G}$ 與其子集 ${\displaystyle H\subseteq G}$，如果 ${\displaystyle H}$ 對 ${\displaystyle G}$ 的群乘法 ${\displaystyle \circ _{G}}$ 和單位元 ${\displaystyle e_{G}\in H}$ 亦構成群，則稱 ${\displaystyle H}$ 為 ${\displaystyle G}$ 的一個子群，常記之為 ${\displaystyle H\leq G}$。

可以證明，可通過以下判據校驗群 ${\displaystyle G}$ 的子集 ${\displaystyle H}$ 是否爲其子群：${\displaystyle H\leq G\Leftrightarrow \forall g,\,h\in H,\,g^{-1}h\in H}$。

前文所述的例子中，單位元與旋轉構成其一個子群 ${\displaystyle R=\left\{\operatorname {id} ,\,r_{1},\,r_{2},\,r_{3}\right\}}$，在上面的表格中突出為紅色：任意兩個旋轉，其複合仍爲旋轉，且任意旋轉可被一個相反方向上的旋轉所抵消。

了解子群族對於作為一個整體來理解群是重要的。^[d]

給定群 ${\displaystyle G}$ 的任意子集 ${\displaystyle S\subseteq G}$，稱由 ${\displaystyle S}$ 生成的子群為 ${\displaystyle \langle S\rangle =\left\{e,s_{1}s_{2}\cdots s_{n}\colon \,\forall i,\,s_{i}\in S\cup S^{-1}\right\}}$，其中 ${\displaystyle S^{-1}:=\left\{s^{-1}\colon \,s\in S\right\}}$。這是包含 ${\displaystyle S}$ 的 ${\displaystyle G}$ 的最小子群，^[24]由 ${\displaystyle S}$ 本身的元素與其反元素的所有可能的有限乘積組成。

同樣在前文所述的二面體群中存在例子：由 ${\displaystyle \left\{r_{2},\,f_{v}\right\}}$ 生成的子群為 ${\displaystyle \left\{\operatorname {id} ,\,r_{2},\,f_{v},\,f_{h}=f_{v}r_{2}\right\}}$。這一集合的確構成群，驗證時需要注意，在該群內有 ${\displaystyle \forall a,a^{2}=\operatorname {id} }$，這也意味着所有元都是自身的反元素，也就是説該群的方次數為 2，關於這一性質，見後文所述之階。

陪集

主條目：陪集

在很多情況下，需要認為兩個元是等同的，如果它們只相差一個給定子群中的元素。例如，在上述 ${\displaystyle D_{4}}$ 中，一旦進行了翻轉，再只進行旋轉而不再進行翻轉，正方形就永遠不能回到 ${\displaystyle r_{2}}$ 的構型，此時可以認爲，旋轉運算對於是否已經進行了翻轉的問題是無關緊要的。陪集可用來把這種現象形式化：子群 ${\displaystyle H}$ 定義了左陪集和右陪集，它們可以認為是把 ${\displaystyle H}$ 平移了一個任意群元素 ${\displaystyle g}$。用符號表示，${\displaystyle H}$ 的包含 ${\displaystyle g}$ 的左和右陪集分別構成集合

${\displaystyle G/H=\left\{xH\colon \,x\in G\right\}}$ 與 ${\displaystyle H\backslash G=\left\{Hx\colon \,x\in G\right\}}$，

其中

左陪集 ${\displaystyle gH=\left\{gh\colon \,h\in H\right\}}$，右陪集 ${\displaystyle Hg=\left\{hg\colon \,h\in H\right\}}$。^[25]

同時也可以定義雙陪集為

${\displaystyle H\backslash G/K=\left\{HxK\colon \,x\in G,\,HxK=\left\{hxk\colon \,h\in H,\,k\in K\right\}\right\}}$，

顯然，左右陪集為雙陪集之特例，取某一側子群為 ${\displaystyle \{e\}}$ 即可。

任何子群 ${\displaystyle H}$ 的陪集形成了 ${\displaystyle G}$ 的一個劃分，換言之，

1. 對任兩個陪集 ${\displaystyle HxK,\,HyK}$，${\displaystyle HxK\cap HyK\neq \varnothing \Leftrightarrow HxK=HyK}$，且
2. 取陪集所有元作無交並有 ${\displaystyle G=\bigsqcup _{x}HxK}$，其中每個 ${\displaystyle x}$ 作爲每個陪集之代表元被選取。

證明

設有 ${\displaystyle HxK\cap HyK\neq \varnothing }$，倘 ${\displaystyle hxk=h'xk'}$，則 ${\displaystyle x:=h^{-1}h'yk'k^{-1}\in HyK}$，即 ${\displaystyle HxK\subset HHyKK=HyK}$；同理 ${\displaystyle HyK\subset HxK}$。故而矛盾，第一句命題得證。

第二句命題是顯然的，不過須要注意到，代表元的選取依賴於選擇公理。

考慮左右陪集。${\displaystyle H}$ 的左和右陪集可以相等也可以不相等。如果它們相等，就是說對於所有 ${\displaystyle G}$ 中的 ${\displaystyle g}$ 有 ${\displaystyle gH=Hg}$，則 ${\displaystyle H}$ 被稱為正規子群。

在前面介紹的對稱群 ${\displaystyle D_{4}}$ 中，由旋轉構成的子群 ${\displaystyle R}$ 的左陪集 ${\displaystyle gR}$

1. 要麼等於 ${\displaystyle R}$，如果 ${\displaystyle g\in R}$ ；
2. 要麼等於 ${\displaystyle U=f_{v}R=\left\{f_{v},\,f_{d},\,f_{h},\,f_{c}\right\}}$（用綠色突出）。

此處的子群 ${\displaystyle R}$ 還是對 ${\displaystyle D_{4}}$ 正規的，因為有 ${\displaystyle f_{v}R=U=Rf_{v}}$，且對於任何 ${\displaystyle f_{v}}$ 以外的元素也類似。

商群

主條目：商群

有時，在由陪集形成的集合上可以賦予一個滿足群公理的運算，使之成為商群或因子群。這僅在子群正規時可行。給定任何對 ${\displaystyle G}$ 正規的子群 ${\displaystyle N}$，定義由 ${\displaystyle N}$ 決定的商群為

${\displaystyle (G/N,\,\circ )}$，其中 ${\displaystyle \circ \colon \,(xN,\,yN)\mapsto xyN}$。

這個定義是由關聯任何元素 ${\displaystyle g}$ 到它的陪集 ${\displaystyle gN}$ 的映射 ${\displaystyle G\to G/N}$ 是群同態的想法（自身是上面提出的一般結構性考慮的一個實例）所激發的，或者是叫做泛性質的一般抽象考慮。陪集 ${\displaystyle eN=N}$充當了這個群的單位元，在商群中 ${\displaystyle gN}$ 的反元素是 ${\displaystyle (gN)^{-1}=g^{-1}N}$。^[e]

${\displaystyle \cdot }$	${\displaystyle R}$	${\displaystyle U}$
${\displaystyle R}$	${\displaystyle R}$	${\displaystyle U}$
${\displaystyle U}$	${\displaystyle U}$	${\displaystyle R}$
商群 ${\displaystyle D_{4}R}$ 的群表。

商群 ${\displaystyle D_{4}/R}$ 的元素是代表單位元的 ${\displaystyle R}$ 自身和 ${\displaystyle U=f_{v}R}$。商群上的群運算如右側所示。例如，${\displaystyle UU=(f_{v}R)(f_{v}R)=(f_{v}f_{v})R=R}$。子群 ${\displaystyle R=\left\{\operatorname {id} ,\,r_{1},\,r_{2},\,r_{3}\right\}}$ 與其構造的商群 ${\displaystyle D_{4}/R}$ 均交換，而 ${\displaystyle D_{4}}$ 本身並不交換。通過較小的群構造較大的群，例如從子群 ${\displaystyle R}$ 和商群 ${\displaystyle D_{4}/R}$ 構造 ${\displaystyle D_{4}}$，被抽象為叫做半直積的概念。

商群和子群一起形成了用它的展示描述所有群的一種方法：任何群都是這個群的生成元上的自由群模以「關係」子群得到的商群。例如，二面體群D₄可以由兩個元素 r 和 f 生成（比如r = r₁右旋，和 f = f_v 垂直）或任何其他）翻轉），這意味着正方形的所有對稱都是這兩個對稱或它們的反元素的有限復合。與關係在一起

r ⁴ = f ² = (rf )² = 1,^[26]

這個群就完全描述出來了。群的展示還可以被用來構造凱萊圖，它是一種利用圖形來輔助理解離散群的工具。

子群和商群以下列方式相互關聯：G 的子集H 可以被看作單射H → G，就是說任何目標元素都有最多一個映射到它的元素。單射的對立是滿射（所有目標的元素都被映射到了），比如規范映射G → G / N。^[y]通過這些同態理解子群和商群強調了這些定義中內在的結構性概念。一般的說，同態既不是單射也不是滿射。群同態的核與像和第一同構定理研究這個現象。

共軛

主條目：共軛類

如果同一個群中的兩個元素p 和q 滿足關係：p = x⁻¹qx，其中x 也是同一個群中的元素，則稱元素p 和q 共軛。共軛關係是一個等價關係，即它滿足三個性質：共軛是自反的、對稱的和遞移的。

在群中可以找到一個集合，這個集合中每一個元素都相互共軛，而在這個集合以外群的其他部分已經沒有任何元素與他們具有共軛關係了。稱這種集合為群中的一個共軛類。同一個群的兩個類之間一定沒有共同的元素。群中一個元素一定屬於且僅屬於一個類。如果群中沒有元素與該元素共軛，則該元素自成一類。

階

主條目：階 (群論)

群中元素個數稱為群G的階，記為|G|^[27]

主條目：拉格朗日定理 (群論)

子群的階能整除這個群的階^[28]

應用

主條目：群論應用

週期性壁紙引發壁紙群。

平面減去一個（粗體）點的基本群由在這個區域內的環路構成。

群的例子和應用大量存在。起點是上面介紹過的整數的群 Z 帶有加法作為群運算。如果把加法替代為乘法，就得到了乘法群。這些群是抽象代數中重要概念的前身。

群應用於很多數學領域中。數學物件的性質經常是通過將群關聯與數學物件關聯，並研究相應的群的性質來研究的。例如，儒勒·昂利·龐加萊通過引入基本群創立了現在所謂的代數拓撲。^[29]通過這種連接方式，拓撲性質比如臨近和連續轉換成了群的性質。^[i]例如，右側的圖像描繪了平面減去一個點的基本群的元素。這個群的元素給出為在這個區域內的環路。藍色環路被認為是零同倫（因此是無關緊要的），因為它可以收縮為一個點。圓孔的存在防止了橙色環路被收縮。橙色環路（或任何環繞這個圓孔一次的其他環路）所生成的，去掉了一個點的平面的基本群是無限循環群。基本群以這種方式探測到了這個圓孔。

在更新近的應用中，影響已經被倒轉過來，由群論背景來激發幾何結構了。^[j]在類似的脈絡下，幾何群論採用了幾何概念，比如在雙曲群的研究中。^[30]其他一些大量應用群論的數學分支包括代數幾何和數論。例如，古典群和皮卡德群在代數幾何上有重要應用；參見^[31]

除了上述理論應用之外，還存在很多群的實踐應用。密碼學依賴於抽象群論方式和從計算群論中特別是實現於有限群上的時候所得到的算法知識的結合。^[32]群論的應用不限於數學；科學如物理、化學和計算機科學都受益於這個概念。

數

很多數系統，比如整數和有理數享有自然給予的群結構。在某些情況下比如對於有理數，加法和乘法運算二者都引發群結構。這種系統是叫做環和體的更一般的代數結構的前身。

整數

整數Z在加法下的群記為（Z, +），它在上面已經描述了。整數帶有用乘法替代加法的運算，(Z, ·)不形成群。閉合、結合律和單位元公理滿足，但反元素不存在：例如，a = 2是整數，但方程a·b = 1的唯一解在這種情況下是b = 1/2，它是有理數而非整數。因此不是所有Z的元素都有（乘法）反元素。^[k]

有理數

對乘法反元素存在的要求建議了考慮分式

${\displaystyle {\frac {a}{b}}}$。

整數的分式（要求b非零）叫做有理數。^[l]所有這種分數的集合通常記為Q。對於有理數帶有乘法(Q,·),成為群仍有一個小障礙：因為有理數0沒有乘法反元素（就是說沒有x使得x·0 = 1），(Q, ·)仍然不是群。

但是，所有非零有理數的集合Q\{0} = {q ∈ Q, q ≠ 0}形成一個在乘法下的阿貝爾群，記為(Q\{0},·)。^[m]結合律和單位元公理從整數的性質中得出。閉合要求在去掉零之後仍成立，因為任何兩個非零有理數的乘積永遠不是零。最後，a/b的反元素是b/a，所以反元素公理也滿足。

有理數（包括0）在加法下也形成群。同時帶有加法和乘法運算產生更復雜的結構叫做環—如果同時除法總是可能的話（如在Q中）就是域，它在抽象代數中佔據中心位置。群論理論因此位於這些實體的理論的底層部分。^[n]

非零整數模以質數

對於任何質數p，模算術提供了整數模以p的乘法群。^[33]群的元素是不能被p整除的整數模p的同餘類，就是說兩個數被認為是等價的如果它們的差被p整除。例如，如果p = 5，則精確地有四個群元素1, 2, 3, 4:排除了5的倍數而6和−4都等價於1。群運算給出為乘法。因此4·4 = 1，因為通常意義下的乘積16等價於1,而5整除16 − 1 = 15。以上事實記為

16 ≡ 1（mod 5）。

p的首要作用是確保了兩個都不被p整除的整數的乘積也不被p整除，因此指示的同餘類的集合在乘法下閉合。^[o]單位元如平常的乘法群一樣是1，而結合律可以從整數的相應性質得出。最後，反元素公理要求給定不整除於p的整數a，存在一個整數b使得

a · b ≡ 1（mod p），就是說p整除a·b − 1的差。

反元素b可以使用貝祖等式和最大公約數gcd(a, p)等於1的事實找到。^[34]在上述p = 5的情況下，4的反元素是4，3的反元素是2，因為3·2 = 6 ≡ 1 (mod 5)。所有的群公理都滿足。實際上，這個例子類似於上述（Q\{0},·），因為它是在有限體F_p中非零元素的乘法群，記為F_p^×。^[35]這些群對於公開密鑰加密是至關重要的。^[p]

循環群

主條目：循環群和阿貝爾群

單位一的六次複數根形成一個循環群。z是本原元而z²不是，因為z的奇數冪不是z²的冪。

循環群是其所有元素都是特定元素a的冪的群（在群運算被寫為加法的時候使用術語倍數）。^[36]在乘法符號下，群的元素是：

..., a⁻³, a⁻², a⁻¹, a⁰ = e, a, a², a³, ...,

這裏的a²意味着a·a，而a⁻³表示a⁻¹·a⁻¹·a⁻¹=(a·a·a)⁻¹等等。^[h]這個元素a叫做這個群的生成元或本原元。

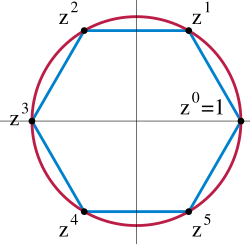
這類群的典型例子是單位一的n次複數根，由滿足zⁿ = 1的複數z給出，其運算為乘法。^[37]任何有n個元素的循環群同構於這個群。使用某些體論，群F_p^×可以被證明為是循環群：對於p = 5, 3是生成元因為3¹ = 3, 3² = 9 ≡ 4, 3³ ≡ 2,而3⁴ ≡ 1。無限循環群同構於（Z, +），它是前面介紹的整數在加法下的群。^[38]因為這兩個原型都是阿貝爾群，所以任何循環群都是。

阿貝爾群包括有限生成阿貝爾群的基本定理的研究是非常成熟的；對這個事態的反映是很多有關群論的概念，比如中心和交換子，描述了一個給定群不是阿貝爾群的程度。^[39]

對稱群

主條目：空間對稱群

參見：分子對稱性、空間群和對稱性 (物理學)

對稱群是由給定數學對象的對稱組成的群，對稱源於它們的幾何本性（比如前面介紹的正方形的對稱群）或源於代數本性（比如多項式方程和它們的解）。^[40]概念上說，群論可以被認為是對稱性的研究。^[t] 數學中的對稱性極大的簡化了幾何或分析對象的研究。群被稱為作用於另一個數學對象X上，如果所有群元素進行某個在X上的運算兼容於群定律。在下面最右側例子中，7階的（2,3,7）三角群的一個元素通過置換突出的彎曲的三角形作用在鑲嵌上（其他的元素也是）。通過群作用，群模式被連接到了所作用到的對象的結構上。

旋轉和翻轉形成一個大二十面體的對稱群。

在化學領域中，比如晶體學、空間群和點群描述分子對稱性和晶體對稱性。這些對稱性位於這些系統的化學和物理表現的底層，而群論使簡化對這些性質的量子力學分析成為可能。^[41]例如，群論被用來證實在特定量子級別間不出現光學躍遷簡單的因為涉及到了狀態的對稱性。

群不只對評定在分子中蘊含的對稱性有用，而且令人驚奇的它們還可以預測出分子的對稱性有時候可以改變。姜-泰勒效應是高對稱的分子的變形，此時，在通過分子的對稱運算相互關聯的一組可能基態中，該分子將採納一個特定的低對稱的基態。^[42][43]

同樣的，群論還可以幫助預測在物質經歷相變的時候出現的物理性質的變更，比如晶體形式從立方體變為四面體。一個例子是鐵電物質，這裏從順電到鐵電狀態的變更出現在居里溫度時，與從高對稱順電狀態到低對稱鐵電狀態的變更有關，並伴隨着所謂的軟聲子模式，它是在變化時轉到零頻率的振動晶格模式。^[44]

這種自發對稱性破缺在基本粒子物理中找到了進一步應用，這裏它的出現與戈德斯通玻色子的出現有關。

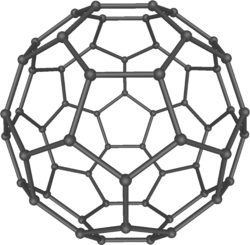
富勒烯展現了二十面體對稱。	氨NH3。它的對稱群是6階的，用120°旋轉和反射生成的。	立方烷C8H8刻畫了八面體對稱。	六水合銅（II）配合物[Cu(OH2)6]2+。相較於完美的對稱形狀，分子垂直膨脹大約22%（姜-泰勒效應）。	（2,3,7）三角群是雙曲群，它作用在這個雙曲面的鑲嵌上。

有限對稱群比如馬蒂厄群被用於編碼理論中，它又用於傳輸數據的糾錯和CD播放器中。^[45]另一個應用是微分伽羅瓦理論，它刻畫有已知形式的不定積分的函數，給出何時特定微分方程的解有良好表現的群論判定標準。^[u]在群作用下保持穩定的幾何性質在幾何不變量理論中研究。^[46]

一般線性群和表示理論

主條目：一般線性群和群表示論

兩個向量（左側展示），和它們乘以矩陣之後（中間和右側展示）。中間的表示了順時針旋轉90°，而右側的再按因子2伸縮了x坐標。

矩陣群由矩陣加上矩陣乘法一起構成。一般線性群GL(n, R)由所有可逆的n乘n的帶有實數元素的矩陣構成。^[47]它的子群被稱為矩陣群或線性群。上面提及的二面體群例子可以被看作（非常小的）矩陣群。另一個重要矩陣群是特殊正交群SO(n)。它描述了n維的所有可能旋轉。通過歐拉角，旋轉矩陣被用於計算機圖形學中。^[48]

表示理論是對群概念的應用並且對深入理解群是很重要的。^[49][50]它通過群作用於其他空間來研究群。一類廣泛的群表示是線性表示，就是說群作用在線性空間中，比如三維歐幾里得空間R³。G在n-維實向量空間上的表示簡單的是從群到一般線性群的群同態

ρ: G → GL(n, R)。

以這種方式，抽象給出的群運算被轉換成用明確的計算可觸及到的矩陣乘法。^[w]

給定一個群作用，這給出了研究所作用的對象的進一步方法。^[x]在另一方面，它還產生了關於群的資訊。群表示是在有限群、李群、代數群和拓撲群特別是（局部）緊群理論中的起組織作用的原則。^[49][51]

伽羅瓦群

主條目：伽羅瓦群

伽羅瓦群是通過對求解多項式方程的過程中涉及到的對稱性的研究而被發展起來的。^[52][53]例如，二次方程ax² + bx + c = 0的解給出為

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$。

對換表達式中的"+"和"−"，也就是置換方程的兩個解可以被看作（非常簡單的）群運算。類似的公式對於三次方程和四次方程也有，但是對於五次方程和更高次的方程就不普遍性的存在。^[54]與多項式相關聯的伽羅瓦群的抽象性質（特別是它們的可解性）給出了那些多項式的所有解都可用根式表達的判定標準，就是說這些解可以類似上面公式那樣只使用加法、乘法和方根來表達。^[55]

這個問題可以使用體論來處理：考慮一個多項式的分裂體就把問題轉移到了體論的領域中了。現代伽羅瓦理論把上述類型的伽羅瓦群推廣到了體擴張，並通過伽羅瓦理論基本定理建立了在體和群之間的嚴格關聯，再次凸顯了群在數學中無所不在。

有限群

主條目：有限群

一個群被稱為有限群，如果它有有限個元素。元素的數目叫做群G的階。^[56]一類重要的有限群是n次對稱群S_N，它是N個字母的置換的群。例如，在3個字母上的n次對稱群S₃是由三個字母ABC的所有可能置換構成的群，就是說它包含元素ABC, ACB, ...,直到CBA，總共有6（或3的階乘）個元素。這類群是基礎性的，因為任何有限群都可以表達為n次對稱群S_N在適合的整數N下的子群（凱萊定理）。相似於上述正方形的對稱的群，S₃還可以解釋為等邊三角形的對稱的群。

在群G中的一個元素a的階是最小的使得aⁿ = e的正整數n，這裏的 aⁿ表示${\displaystyle \underbrace {a\cdot \ldots \cdot a} _{n}}$，就是應用運算·於a的n個復本上。（如果·代表乘法則aⁿ對應於a的n次冪）。在無限群中，這個n可能不存在，在這種情況下a的階被稱為無限的。一個元素的階等於這個元素生成的循環子群的階。

更復雜的計數技術例如計數陪集，產生關於有限群的更精確陳述：拉格朗日定理聲稱有限群G的任何有限子群H的階整除G的階。西羅定理證明了它的部分逆命題。

上面討論的二面體群是8階有限群。r₁的階為4，這是它生成的子群R（見上）的階。反射元素f_v等的階是2。如拉格朗日定理所述這兩個階都整除8。上面的群F_p^×有階p − 1。

有限單純群分類

主條目：有限單純群分類

數學家們常常為尋求一種數學物件的完備的分類（或列表）而努力。並且這種分類是十分有用的: 如果有限群有一個完備的列表, 假設我們需要證明定理P時, 如果可以一步一步證明定理對列表中給出的群成立, 那我們即可證明定理P在有限群的領域內成立。這個目標迅速引出了一系列困難而意義深遠的數學問題。
根據拉格朗日定理，p階有限群（p為質數）必定是循環（阿貝爾群）群Z_p。
p²階群也被證明是阿貝爾群。但這一命題並不能推廣到p³階群，如上面的非阿貝爾群——8階二面體群 ${\displaystyle \mathrm {D} _{4}}$ 所示，其中 8 = 2³。^[57]可以利用計算機代數系統來給較小的群列表，但沒有對一切有限群的分類。^[q] 一個中間步驟是有限單純群分類。^[r]如果一個非平凡群僅有的正規子群是平凡群和它自身，那麼這個群叫做一個單純群或簡單純群。^[s]合成列說明單純群可以作為建構有限群的「磚塊」。^[58] 有限單純群分類是當代群論的一個主要成就。1998年的菲爾茲獎得主理查德·博赫茲成功地證明了怪獸月光理論。該猜想指出了有限單純群中分類中的最大的散在群——「怪獸群」與一種來自經典複分析和弦理論（一種被認為統一了對許多物理學現象的描述的理論）的物件模函數之間的驚人而深刻的聯繫。^[59]

帶有額外結構的群

很多群同時是群和其他數學結構的例子。用范疇論的語言來說，它們是在范疇中的「群」物件，這意味着它們是帶着模仿群公理的（叫做態射的）變換的對象（可以是其他代數/數學結構）。例如，所有群（如上面定義的）也是一個集合，所以群是在集合范疇中的群物件。

拓撲群

主條目：拓撲群

在複平面中的單位圓在複數乘法下是李群，所以是拓撲群。它是拓撲的因為複數乘法和除法是連續的。它是流形並因此是李群，因為所有小段比如在圖中的紅色圓弧，看起來像（顯示在底下的）實數線的一部分。

某些拓撲空間可以配備上群結構。為了讓群公理與拓撲交織良好，群運算必須是連續函數，就是說如果g和h只變化很小，那麼g·h,和g⁻¹必須變化不大。這種群叫做拓撲群，並且它們是在拓撲空間范疇內的群對象。^[60]最基本的例子是實數R在加法之下(R\{0},·)，任何其他拓撲體比如複數或p進數也是類似。所有這些群都是局部緊拓撲群，所以它們有哈爾測度並可以通過調和分析來研究。前者提供了不變積分的抽象形式化。以實數情況為例，不變性意味着有：

${\displaystyle \int f(x)\,dx=\int f(x+c)\,dx}$

對於任何常數c成立。在這些體上的矩陣群也屬於這種結構下，賦值向量環和賦值向量代數群也是如此，它們對數論是基礎性的。^[61]無限體擴張的伽羅瓦群比如絕對伽羅瓦群也可以配備上拓撲，叫做Krull拓撲，它又是推廣上面概述的體和群的連接到無限體擴張的中心概念。^[62]適應代數幾何需要的這個想法的高級推廣是étale基本群。^[63]

李群

主條目：李群 (數學)

李群（為紀念索菲斯·李而命名）是具有流形結構的群，就是說它們是局部上看起來像某個適當維度的歐幾里得空間的空間。^[64]這裏，作為額外結構的流形結構也必須是兼容的，就是說對應於乘法和求逆的映射必須是光滑的。

標準例子是上面介紹的一般線性群：它是所有${\displaystyle n\times n}$矩陣的空間的開子集，因為它由不等式

det (A) ≠ 0，

給出。這裏的A指示${\displaystyle n\times n}$矩陣。^[65]

李群在物理中是基礎性的：諾特定理把連續對稱與守恆定律關聯起來。^[66]在空間和時間中旋轉和平移不變性是力學定律的基本對稱。它們可以被用來構造簡單的模型——比如在一種狀況下實施軸對稱常常會導致在解用來提供物理描述的方程上的重大簡化。^[v]另一個例子是勞侖茲變換，它有關於兩個相互運動的觀察者的時間和速度的測量。它們可以用純群論方式推演，通過把變換表達為閔可夫斯基時空的旋轉對稱。在忽略萬有引力的情況下，後者充當了狹義相對論的時空模型。^[67]閔可夫斯基時空的完全對稱群，就是說包括了平移，叫做龐加萊群。通過上述聯繫，它在狹義相對論中扮演了關鍵角色，並隱含地用於量子場論。^[68] 隨位置變化的對稱與規范場論一起構成現代物理對相互作用的描述的中心。^[69]

推廣

類似群的結構
	完全性	結合律	單位元	除法
群	是	是	是	是
么半群	是	是	是	否
半群	是	是	否	否
環群	是	否	是	是
擬群	是	否	否	是
原群	是	否	否	否
廣群	否	是	是	是
範疇	否	是	是	否

在抽象代數中，通過放鬆定義群的某個公理可定義出更多的一般結構。^[21][70][71]例如，如果省略所有元素都反元素的要求，結果的代數結構就叫做么半群。自然數集N（包括0）在加法下形成了么半群，還有非零整數在乘法下(Z\{0},·)也是。有一種一般方法用來向任何（阿貝爾的）么半群正式的增加元素的反元素，非常類似於從(Z\{0},·)得出(Q\{0},·)的方式，這叫做格羅滕迪克群。廣群非常類似於群，除了復合a · b不必須在所有的a和b上有定義之外。它們由更加復雜形式的對稱的研究所引發，常見於拓撲和分析結構比如基本廣群中。表格給出一些推廣群的結構。

參見

• 子群
• 群子集的乘積
• 正規子群
• 同構基本定理
• 有限群
• 中心化子和正規化子
• 拉格朗日定理
• 可解群
• 冪零群
• 半群
• 舒爾正交關係

註釋

^  a:  《數學評論》列出了3,224篇2005年寫的關於群論和它的應用的研究論文。

^  b:  閉合公理已經由·是二元運算的條件所蘊含。因此有些作者省略這個公理。Lang 2002。

^  c:  比如參見Lang (2002, 2005)和Herstein (1996, 1975)的書。

^  d:  但是一個群不由它的子群的格所決定。參見Suzuki 1951。

^  e:  群運算的這麼規范的擴展是泛性質的實例。

^  f:  例如，依據拉格朗日定理，如果G是有限的，則任何子群和任何商群的大小整除G的大小。

^  g:  詞同態演化自希臘語ὁμός—相同和μορφή—結構。

^  h:  循環群的加法符號是t·a, t ∈ Z。

^  i:  例子參見塞弗特－范坎彭定理。

^  j:  一個例子是群的群上同調，它等於它的分類空間的單同調。

^  k:  有乘法反元素的元素叫做可逆元素，參見Lang 2002, §II.1, p. 84。

^  l:  通過增加分數的從整數到有理數的轉變推廣為分式體。

^  m:  用任何體F替代Q同樣是真的。參見Lang 2005, §III.1, p. 86。

^  n:  例如，體的乘法群的有限子群必然是循環群。參見Lang 2002, Theorem IV.1.9。模和單純代數的撓概念是這個原理的另一個實例。

^  o:  陳述的性質是質數的一個可能定義。參見質元素。

^  p:  例如，迪菲-赫爾曼密鑰交換協議使用離散對數。

^  q:  階不超過2000的群是已知的。這些群在同構意義下約有490億個。參見Besche, Eick & O'Brien 2001.

^  r:  在單純群和一般群分類之間的缺口在於擴張問題，一個很難一般性求解的問題。參見Aschbacher 2004, p. 737.

^  s:  等價地說，一個非平凡群是單純群當且僅當它僅有的商群是平凡群和自身。參見Michler 2006, Carter 1989.

^  t:  更嚴格的說，所有群都是某個圖的對稱群，參見Frucht 1939。

^  u:  更精確地說，monodromy作用在要考慮的微分方程的解的向量空間上。參見Kuga 1993, pp. 105–113。

^  v:  例如參見史瓦西度規，這裏的對稱極大的減小了物理系統的復雜性。

^  w:  例如，這是有限簡單群的分類的關鍵。參見Aschbacher 2004。

^  x:  例如，群作用在單模上的效果的Schur引理。更加復雜的例子是絕對伽羅瓦群作用在平展餘調上。

^  y:  單射和滿射分別對應於單同態和滿同態。在傳給對偶范疇的時候它們是可互換的。

引文

1. Herstein 1975, §2, p. 26
2. Hall 1967, §1.1, p. 1:「群的想法遍佈在包括純數學和應用數學二者的整個數學中。」
3. Wussing 2007
4. Kleiner 1986
5. Smith 1906
6. Galois 1908
7. Kleiner 1986, p. 202
8. Cayley 1889
9. Wussing 2007, §III.2
10. Lie 1973
11. Kleiner 1986, p. 204
12. Wussing 2007, §I.3.4
13. Jordan 1870
14. von Dyck 1882
15. Curtis 2003
16. Mackey 1976
17. Borel 2001
18. Aschbacher 2004
19. Herstein 1975, §2.1, p. 27
20. Lang 2005, App. 2, p. 360
21. Mac Lane 1998
22. Lang 2005, §II.3, p. 34
23. Lang 2005, §II.1, p. 19
24. Ledermann 1973, §II.12, p. 39
25. Lang 2005, §II.4, p. 41
26. Lang 2002, §I.2, p. 9
27. 韓士安,林磊. 近世代数（第二版）. 北京: 科學出版社. 2009: 8. ISBN 9787030250612.
28. [美] 約翰·德比希爾. 代数的历史：人类对未知量的不舍追踪（修订版）. 人民郵電出版社. ISBN 9787115225375 （簡體中文）. 關於群結構的第一個偉大定理是拉格朗日定理：子群的階整除這個群的階。整除的商被稱為這個子群的指數。根據拉格朗日定理，分數指數不會出現。我們可以在 6 階群中找到階為 2 或 3（指數分別為 3 或 2）的子群，但是我們永遠不可能在其中找到階為 4 或 5 的子群，因為 6 不能被 4 或 5 整除。 引文格式1維護：未識別語文類型 (link)
29. Hatcher 2002, Chapter I, p. 30
30. Coornaert, Delzant & Papadopoulos 1990
31. Neukirch 1999，特別是§§I.12和I.13
32. Seress 1997
33. Lang 2005, Chapter VII
34. Rosen 2000, p. 54 (Theorem 2.1)
35. Lang 2005, §VIII.1, p. 292
36. Lang 2005, §II.1, p. 22
37. Lang 2005, §II.2, p. 26
38. Lang 2005, §II.1, p. 22 (example 11)
39. Lang 2002, §I.5, p. 26, 29
40. Weyl 1952
41. Conway, Delgado Friedrichs & Huson et al. 2001.另見Bishop 1993
42. Bersuker, Isaac, The Jahn-Teller Effect, Cambridge University Press: 2, 2006, ISBN 0521822122
43. Jahn & Teller 1937
44. Dove, Martin T, Structure and Dynamics: an atomic view of materials, Oxford University Press: 265, 2003, ISBN 0198506783
45. Welsh 1989
46. Mumford, Fogarty & Kirwan 1994
47. Lay 2003
48. Kuipers 1999
49. Fulton & Harris 1991
50. Serre 1977
51. Rudin 1990
52. Robinson 1996, p. viii
53. Artin 1998
54. Lang 2002, Chapter VI (see in particular p. 273 for concrete examples)
55. Lang 2002, p. 292 (Theorem VI.7.2)
56. Kurzweil & Stellmacher 2004
57. Artin 1991, Theorem 6.1.14.另見Lang 2002, p. 77，其中包含類似結果。
58. Lang 2002, §I. 3, p. 22
59. Ronan 2007
60. Husain 1966
61. Neukirch 1999
62. Shatz 1972
63. Milne 1980
64. Warner 1983
65. Borel 1991
66. Goldstein 1980
67. Weinberg 1972
68. Naber 2003
69. Becchi 1997
70. Denecke & Wismath 2002
71. Romanowska & Smith 2002

引用

一般引用

• Artin, Michael, Algebra, Prentice Hall, 1991, ISBN 978-0-89871-510-1, Chapter 2 contains an undergraduate-level exposition of the notions covered in this article.
• Devlin, Keith, The Language of Mathematics: Making the Invisible Visible, Owl Books, 2000, ISBN 978-0-8050-7254-9, Chapter 5 provides a layman-accessible explanation of groups.
• Dummit, David S.; Foote, Richard M., Abstract algebra 3rd, New York: Wiley, 2004, ISBN 978-0-471-43334-7, MR2286236.
• Fulton, William; Harris, Joe, Representation theory. A first course, Graduate Texts in Mathematics, Readings in Mathematics 129, New York: Springer-Verlag, 1991, ISBN 978-0-387-97495-8, MR1153249, ISBN 978-0-387-97527-6
• Hall, G. G., Applied group theory, American Elsevier Publishing Co., Inc., New York, 1967, MR0219593, an elementary introduction.
• Herstein, Israel Nathan, Abstract algebra 3rd, Upper Saddle River, NJ: Prentice Hall Inc., 1996, ISBN 978-0-13-374562-7, MR1375019.
• Herstein, Israel Nathan, Topics in algebra 2nd, Lexington, Mass.: Xerox College Publishing, 1975, MR0356988.
• Lang, Serge, Algebra, Graduate Texts in Mathematics 211, Berlin, New York, 2002, ISBN 978-0-387-95385-4, MR1878556.
• Lang, Serge, Undergraduate Algebra 3rd, Berlin, New York: Springer-Verlag, 2005, ISBN 978-0-387-22025-3.
• Ledermann, Walter, Introduction to the theory of finite groups, Oliver and Boyd, Edinburgh and London, 1953, MR0054593.
• Ledermann, Walter, Introduction to group theory, New York: Barnes and Noble, 1973, OCLC 795613.
• Robinson, Derek John Scott, A course in the theory of groups, Berlin, New York: Springer-Verlag, 1996, ISBN 978-0-387-94461-6.
• 《代數學引論》第二版ISBN 7-04-008893-2聶靈沼、丁石孫著，高等教育出版社出版

專門引用

• Artin, Emil, Galois Theory, New York: Dover Publications, 1998, ISBN 978-0-486-62342-9.
• Aschbacher, Michael, The Status of the Classification of the Finite Simple Groups (PDF), Notices of the American Mathematical Society, 2004, 51 (7): 736–740 [2008-09-13], ISSN 0002-9920, （原始內容存檔 (PDF)於2011-06-05）.
• Becchi, C., Introduction to Gauge Theories, 1997 [2008-05-15], （原始內容存檔於2016-10-07）.
• Besche, Hans Ulrich; Eick, Bettina; O'Brien, E. A., The groups of order at most 2000, Electronic Research Announcements of the American Mathematical Society, 2001, 7: 1–4 [2008-09-13], doi:10.1090/S1079-6762-01-00087-7, MR1826989, （原始內容存檔於2008-10-08）.
• Bishop, David H. L., Group theory and chemistry, New York: Dover Publications, 1993, ISBN 978-0-486-67355-4.
• Borel, Armand, Linear algebraic groups, Graduate Texts in Mathematics 126 2nd, Berlin, New York: Springer-Verlag, 1991, ISBN 978-0-387-97370-8, MR1102012.
• Carter, Roger W., Simple groups of Lie type, New York: John Wiley & Sons, 1989, ISBN 978-0-471-50683-6.
• Conway, John Horton; Delgado Friedrichs, Olaf; Huson, Daniel H.; Thurston, William P., On three-dimensional space groups, Beiträge zur Algebra und Geometrie, 2001, 42 (2): 475–507 [2008-09-13], ISSN 0138-4821, MR1865535, （原始內容存檔於2020-06-01）.
• （法文） Coornaert, M.; Delzant, T.; Papadopoulos, A., Géométrie et théorie des groupes [Geometry and Group Theory], Lecture Notes in Mathematics 1441, Berlin, New York: Springer-Verlag, 1990, ISBN 978-3-540-52977-4, MR1075994.
• Denecke, Klaus; Wismath, Shelly L., Universal algebra and applications in theoretical computer science, London: CRC Press, 2002, ISBN 978-1-58488-254-1.
• Fröhlich, Albrecht, Formal groups, Lecture notes in mathematics 74, Berlin, New York: Springer-Verlag, 1968.
• （德文） Frucht, R., Herstellung von Graphen mit vorgegebener abstrakter Gruppe [Construction of Graphs with Prescribed Group], Compositio Mathematica, 1939, 6: 239–50, ISSN 0010-437X, （原始內容存檔於2008-12-01）.
• Goldstein, Herbert, Classical Mechanics 2nd, Reading, MA: Addison-Wesley Publishing: 588–596, 1980, ISBN 0-201-02918-9.
• Hatcher, Allen, Algebraic topology, Cambridge University Press, 2002 [2008-09-13], ISBN 978-0-521-79540-1, （原始內容存檔於2018-05-19）.
• Husain, Taqdir, Introduction to Topological Groups, Philadelphia: W.B. Saunders Company, 1966, ISBN 978-0-89874-193-3
• Jahn, H.; Teller, E., Stability of Polyatomic Molecules in Degenerate Electronic States. I. Orbital Degeneracy, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences (1934-1990), 1937, 161 (905): 220–235, doi:10.1098/rspa.1937.0142.
• Kassel, Christian, Quantum Groups, Springer, 1994, ISBN 978-0387943701.
• Kuipers, Jack B., Quaternions and rotation sequences - A primer with applications to orbits, aerospace, and virtual reality, Princeton University Press, 1999, ISBN 978-0-691-05872-6, MR1670862.
• Kuga, Michio, Galois' dream: group theory and differential equations, Boston, MA: Birkhäuser Boston, 1993, ISBN 978-0-8176-3688-3, MR1199112.
• Kurzweil, Hans; Stellmacher, Bernd, The theory of finite groups, Universitext, Berlin, New York: Springer-Verlag, 2004, ISBN 978-0-387-40510-0, MR2014408.
• Lay, David, Linear Algebra and Its Applications, Addison-Wesley, 2003, ISBN 978-0-201-70970-4.
• Mac Lane, Saunders, Categories for the Working Mathematician 2nd, Berlin, New York: Springer-Verlag, 1998, ISBN 978-0-387-98403-2.
• Michler, Gerhard, Theory of finite simple groups, Cambridge University Press, 2006, ISBN 978-0-521-86625-5.
• Milne, James S., Étale cohomology, Princeton University Press, 1980, ISBN 978-0-691-08238-7
• Mumford, David; Fogarty, J.; Kirwan, F., Geometric invariant theory 34 3rd, Berlin, New York: Springer-Verlag, 1994, ISBN 978-3-540-56963-3, MR1304906.
• Naber, Gregory L., The geometry of Minkowski spacetime, New York: Dover Publications, 2003, ISBN 978-0-486-43235-9, MR2044239.
• Neukirch, Jürgen, Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften 322, Berlin: Springer-Verlag, 1999, ISBN 978-3-540-65399-8, MR1697859
• Romanowska, A.B.; Smith, J.D.H., Modes, World Scientific, 2002, ISBN 9789810249427.
• Ronan, Mark, Symmetry and the Monster: The Story of One of the Greatest Quests of Mathematics, Oxford University Press, 2007, ISBN 978-0-19-280723-6.
• Rosen, Kenneth H., Elementary number theory and its applications 4th, Addison-Wesley, 2000, ISBN 978-0-201-87073-2, MR1739433.
• Rudin, Walter, Fourier Analysis on Groups, Wiley Classics, Wiley-Blackwell, 1990, ISBN 047152364X.
• Seress, Ákos, An introduction to computational group theory, Notices of the American Mathematical Society, 1997, 44 (6): 671–679, ISSN 0002-9920, MR1452069, （原始內容存檔於2007-02-08）.
• Serre, Jean-Pierre, Linear representations of finite groups, Berlin, New York: Springer-Verlag, 1977, ISBN 978-0-387-90190-9, MR0450380.
• Shatz, Stephen S., Profinite groups, arithmetic, and geometry, Princeton University Press, 1972, ISBN 978-0-691-08017-8, MR0347778
• Suzuki, Michio, On the lattice of subgroups of finite groups, Transactions of the American Mathematical Society, 1951, 70 (2): 345–371, doi:10.2307/1990375.
• Warner, Frank, Foundations of Differentiable Manifolds and Lie Groups, Berlin, New York: Springer-Verlag, 1983, ISBN 978-0-387-90894-6.
• Weinberg, Steven, Gravitation and Cosmology, New York: John Wiley & Sons, 1972, ISBN 0-471-92567-5.
• Welsh, Dominic, Codes and cryptography, Oxford: Clarendon Press, 1989, ISBN 978-0-19-853287-3.
• Weyl, Hermann, Symmetry, Princeton University Press, 1952, ISBN 978-0-691-02374-8.

歷史引用

參見：群論在歷史上的重要出版物。

• Borel, Armand, Essays in the History of Lie Groups and Algebraic Groups, Providence, R.I.: American Mathematical Society, 2001, ISBN 978-0-8218-0288-5
• Cayley, Arthur, The collected mathematical papers of Arthur Cayley, II (1851 - 1860), Cambridge University Press, 1889.
• Curtis, Charles W., Pioneers of Representation Theory: Frobenius, Burnside, Schur, and Brauer, History of Mathematics, Providence, R.I.: American Mathematical Society, 2003, ISBN 978-0-8218-2677-5.
• （德文） von Dyck, Walther, Gruppentheoretische Studien Group-theoretical Studies (subscription required), Mathematische Annalen, 1882, 20 (1): 1–44, ISSN 0025-5831, doi:10.1007/BF01443322^{[永久失效連結]}.
• （法文） Galois, Évariste, Tannery, Jules , 編, Manuscrits de Évariste Galois [Évariste Galois' Manuscripts], Paris: Gauthier-Villars, 1908 [2008-09-13], （原始內容存檔於2011-05-21） (Galois work was first published by Joseph Liouville in 1843).
• （法文） Jordan, Camille, Traité des substitutions et des équations algébriques [Study of Substitutions and Algebraic Equations], Paris: Gauthier-Villars, 1870.
• Kleiner, Israel, The evolution of group theory: a brief survey (subscription required), Mathematics Magazine, 1986, 59 (4): 195–215, ISSN 0025-570X, MR863090.
• （德文） Lie, Sophus, Gesammelte Abhandlungen. Band 1 [Collected papers. Volume 1], New York: Johnson Reprint Corp., 1973, MR0392459.
• Mackey, George Whitelaw, The theory of unitary group representations, University of Chicago Press, 1976, MR0396826
• Smith, David Eugene, History of Modern Mathematics, Mathematical Monographs, No. 1, 1906 [2008-09-13], （原始內容存檔於2008-09-19）.
• Wussing, Hans, The Genesis of the Abstract Group Concept: A Contribution to the History of the Origin of Abstract Group Theory, New York: Dover Publications, 2007, ISBN 978-0-486-45868-7.

外部連結

• 埃里克·韋斯坦因. Group. MathWorld.
• Group （頁面存檔備份，存於互聯網檔案館） at PlanetMath.
• The development of group theory （頁面存檔備份，存於互聯網檔案館） at The MacTutor History of Mathematics archive.