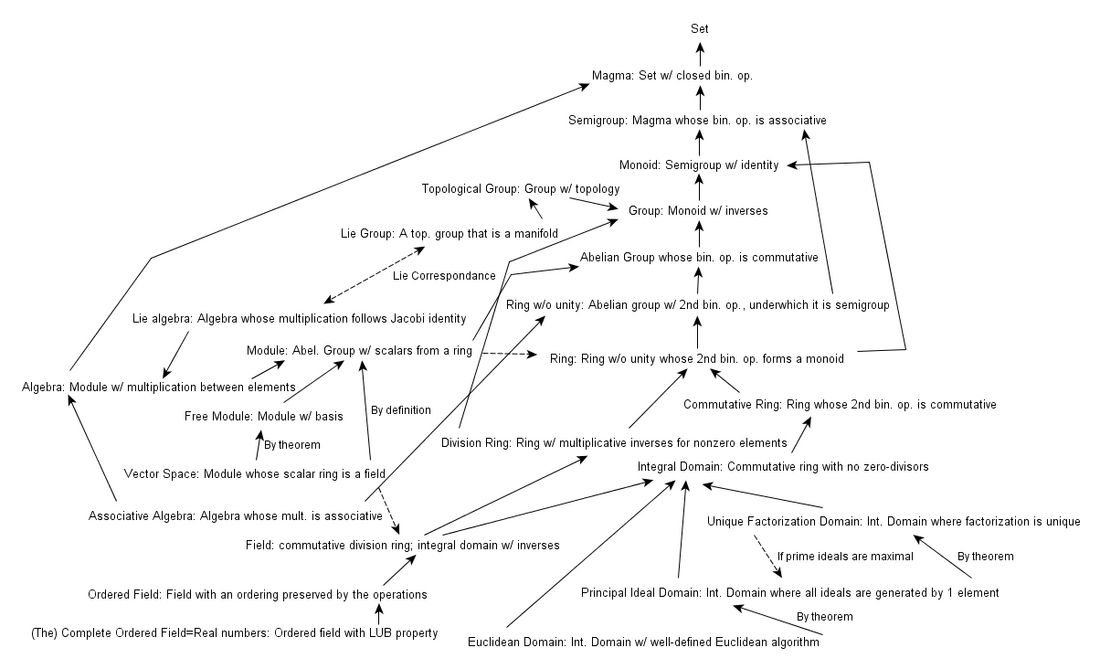
가환환  위에 정의된 리 대수
위에 정의된 리 대수 ![{\displaystyle ({\mathfrak {g}},[\cdot ,\cdot ])}](//wikimedia.org/api/rest_v1/media/math/render/svg/1acf5360abf7b837b08e1298909959fcd868d061) 는
는  -가군
-가군  와 다음을 만족하는 선형 변환
와 다음을 만족하는 선형 변환 ![{\displaystyle [\cdot ,\cdot ]:{\mathfrak {g}}\times {\mathfrak {g}}\to {\mathfrak {g}}}](//wikimedia.org/api/rest_v1/media/math/render/svg/44ce0ecebaaa6530dea73faf9e5831dacb050936) 로 이루어진다.
로 이루어진다.
- (쌍선형성) 모든
 와
와  에 대해
에 대해 ![{\displaystyle [ax+by,z]=a[x,z]+b[y,z],\quad [z,ax+by]=a[z,x]+b[z,y]}](//wikimedia.org/api/rest_v1/media/math/render/svg/730cd19026c1c8b8b3ac4e918cad74872c023d23) 이다.
이다.
- (교대성) 모든
 에 대하여
에 대하여 ![{\displaystyle [x,x]=0}](//wikimedia.org/api/rest_v1/media/math/render/svg/94ccb967db9ab0773c5aa2e0fc234cd33373f193) 이다.
이다.
- (야코비 항등식) 모든
 에 대해
에 대해 ![{\displaystyle [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0}](//wikimedia.org/api/rest_v1/media/math/render/svg/23655a62f2a7cc545f121d9bcc30fe2c56731457) 이다.
이다.
이 이항 연산은 리 괄호(Lie括弧, 영어: Lie bracket)로 불린다. 리 대수의 준동형은 리 괄호를 보존하는 선형 변환이다.
만약  에서 2의 역원
에서 2의 역원  이 존재한다면 (예를 들어,
이 존재한다면 (예를 들어,  가 표수가 2가 아닌 체라면), 교대성을 반대칭성, 즉 모든
가 표수가 2가 아닌 체라면), 교대성을 반대칭성, 즉 모든  에 대하여
에 대하여 ![{\displaystyle [x,y]+[y,x]=0}](//wikimedia.org/api/rest_v1/media/math/render/svg/5ba3f4019700f26de2bd59625e7b078ba3d11929) 인 성질로 대체할 수 있다. (2가 가역원이 아니라면, 교대성이 반대칭성보다 더 강한 조건이다.)
인 성질로 대체할 수 있다. (2가 가역원이 아니라면, 교대성이 반대칭성보다 더 강한 조건이다.)
통상적으로 리 대수는 흑자체 소문자  등으로 나타낸다.
등으로 나타낸다.
정수환  위의 리 대수를 리 환(Lie環, 영어: Lie ring)이라고 부르기도 한다. 이름과 달리 리 환은 (곱셈 결합 법칙을 따르는) 환을 이루지 않는다.
위의 리 대수를 리 환(Lie環, 영어: Lie ring)이라고 부르기도 한다. 이름과 달리 리 환은 (곱셈 결합 법칙을 따르는) 환을 이루지 않는다.
등급 리 대수
환의 개념에 등급을 붙여 등급환을 정의할 수 있는 것처럼, 등급 리 대수(等級Lie代數, 영어: graded Lie algebra)의 개념을 정의할 수 있다.
가환 모노이드  가 주어졌다고 하자. 가환환
가 주어졌다고 하자. 가환환  위의,
위의,  등급을 갖는 등급 리 대수
등급을 갖는 등급 리 대수 ![{\displaystyle ({\mathfrak {g}},[\cdot ,\cdot ])}](//wikimedia.org/api/rest_v1/media/math/render/svg/1acf5360abf7b837b08e1298909959fcd868d061) 는 다음과 같이, 등급이 붙어 있고, 리 괄호가 등급을 보존하는 리 대수이다. 즉,
는 다음과 같이, 등급이 붙어 있고, 리 괄호가 등급을 보존하는 리 대수이다. 즉,

![{\displaystyle [\cdot ,\cdot ]\colon {\mathfrak {g}}_{d}\times {\mathfrak {g}}_{d'}\to {\mathfrak {g}}_{d+d'}}](//wikimedia.org/api/rest_v1/media/math/render/svg/22fcdf15d35825f322069e4116ce069db797bd28)
이다.
리 군론적 성질
리 군론에서, 실수체 또는 복소수체 위의 리 대수는 실수 또는 복소수 리 군과 밀접한 관계를 가진다. 모든 리 군에 대하여, 그 왼쪽 불변 벡터장들은 유한 차원 실수 리 대수를 이루며, 반대로 모든 유한 차원 실수 리 대수는 유일한 연결 단일 연결 리 군의 동형류에 표준적으로 대응한다.
통상적으로, 주어진 리 군의 리 대수는 리 군의 이름의 흑자체 소문자로 쓴다. 예를 들어 SO(5)의 리 대수는  이다.
이다.
보편 대수학적 성질
리 군과 달리, 주어진 체  위의 리 대수들의 모임은 대수 구조 다양체를 이룬다. 이 대수 구조 다양체는 다음과 같은 연산을 갖는다.
위의 리 대수들의 모임은 대수 구조 다양체를 이룬다. 이 대수 구조 다양체는 다음과 같은 연산을 갖는다.
- 0항 연산:
- 1항 연산:
- − (덧셈 역원)
- 임의의
 에 대하여, 스칼라곱
에 대하여, 스칼라곱 
- 2항 연산:
- + (덧셈)
![{\displaystyle [-,-]}](//wikimedia.org/api/rest_v1/media/math/render/svg/7ba9b4dfaeae181a7a507d66e1b54fb640a7c61d) (리 괄호)
(리 괄호)
이는  위의 벡터 공간의 대수 구조에 리 괄호를 추가한 것이다. 이에 따라 자유 리 대수의 개념이나 리 대수의 직접곱을 정의할 수 있다. 유한 개의 리 대수의 직접곱은 직합과 같다.
위의 벡터 공간의 대수 구조에 리 괄호를 추가한 것이다. 이에 따라 자유 리 대수의 개념이나 리 대수의 직접곱을 정의할 수 있다. 유한 개의 리 대수의 직접곱은 직합과 같다.
이 밖에도, 다음과 같은 리 대수들의 모임은 대수 구조 다양체를 이룬다.
- 아벨 리 대수. 이는 항등식
![{\displaystyle [x,y]=0}](//wikimedia.org/api/rest_v1/media/math/render/svg/0bb3ac5611c95c794cec85401f417c5e0146185d) 으로 정의된다.
으로 정의된다.
 형의 멱영 리 대수. 이는 내림 중심렬의 길이가
형의 멱영 리 대수. 이는 내림 중심렬의 길이가  이하인 리 대수이다.
이하인 리 대수이다. 형의 가해 리 대수. 이는 유도열의 길이가
형의 가해 리 대수. 이는 유도열의 길이가  이하인 리 대수이다.
이하인 리 대수이다.
리 대수의 대수 구조 다양체들의 모임 위에는 다음과 같이 이항 연산을 정의할 수 있다. 리 대수의 대수 구조 다양체  ,
,  가 주어졌을 때, 그 곱
가 주어졌을 때, 그 곱  는
는  의 원소들의,
의 원소들의,  에 속한 리 대수 아이디얼에 대한 리 대수 확대로 구성된다.
에 속한 리 대수 아이디얼에 대한 리 대수 확대로 구성된다.
직합
가환환  위의 두 리 대수
위의 두 리 대수  ,
,  가 주어졌을 때, 그 직합
가 주어졌을 때, 그 직합  를 정의할 수 있다. 이는 가군으로서의 직합과 일치하며, 그 위의 리 괄호는 다음과 같이 성분별로 정의된다.
를 정의할 수 있다. 이는 가군으로서의 직합과 일치하며, 그 위의 리 괄호는 다음과 같이 성분별로 정의된다.
![{\displaystyle [g,g']_{{\mathfrak {g}}\oplus {\mathfrak {h}}}=[g,g']_{\mathfrak {g}}\qquad \forall g,g'\in {\mathfrak {g}}}](//wikimedia.org/api/rest_v1/media/math/render/svg/207a589efa7b9e8cbafd94a60ed30877769809a1)
![{\displaystyle [h,h']_{{\mathfrak {g}}\oplus {\mathfrak {h}}}=[h,h']_{\mathfrak {h}}\qquad \forall h,h'\in {\mathfrak {h}}}](//wikimedia.org/api/rest_v1/media/math/render/svg/7788fc94350b6492e43f82b0e6a44f5ab2a5f93d)
![{\displaystyle [g,h]_{{\mathfrak {g}}\oplus {\mathfrak {h}}}=[h,g]_{{\mathfrak {g}}\oplus {\mathfrak {h}}}=0\qquad \forall g\in {\mathfrak {g}},\;h\in {\mathfrak {h}}}](//wikimedia.org/api/rest_v1/media/math/render/svg/7b6814ac937b269176f7d9ab06fc873e59aec12a)
보다 일반적으로,  -리 대수의 집합
-리 대수의 집합  이 주어졌을 때, 그 직합
이 주어졌을 때, 그 직합

를 정의할 수 있다. 마찬가지로,  -리 대수의 집합
-리 대수의 집합  이 주어졌을 때, 그 직접곱
이 주어졌을 때, 그 직접곱

를 정의할 수 있다. 유한 직접곱은 유한 직합과 일치하지만, 무한 직접곱은 일반적으로 무한 직합보다 더 크다.
실수체 위의 리 대수의 직합·직접곱은 리 군의 직접곱에 대응한다. 반면, 리 대수의 텐서곱은 일반적으로 정의될 수 없다.
반직접합
군에 대하여 반직접곱을 정의할 수 있는 것처럼, 두 개의 리 대수의 반직접합(영어: semidirect sum)을 정의할 수 있다. 리 대수의 범주는 아벨 범주를 이루지 못하므로, 직합이 아닌 반직접합이 존재한다.
미분
체  위의 리 대수
위의 리 대수  위의 미분(微分, 영어: derivation)은 다음과 같은
위의 미분(微分, 영어: derivation)은 다음과 같은  -선형 변환이다.
-선형 변환이다.

이는 다음과 같은 곱 규칙을 만족시켜야 한다.
![{\displaystyle \delta [x,y]=[\delta x,y]+[x,\delta y]\qquad \forall x,y\in {\mathfrak {g}}}](//wikimedia.org/api/rest_v1/media/math/render/svg/10ce0eb2ed31d1e4cf0364deca1d6fcb73052f1d)
리 대수  위의 미분들의 벡터 공간을
위의 미분들의 벡터 공간을  라고 쓰자. 이 위에 다음과 같은 리 괄호를 부여한다면 이 역시 리 대수를 이루며, 이를 미분 리 대수(영어: Lie algebra of derivations)
라고 쓰자. 이 위에 다음과 같은 리 괄호를 부여한다면 이 역시 리 대수를 이루며, 이를 미분 리 대수(영어: Lie algebra of derivations)  라고 한다.
라고 한다.
![{\displaystyle [\delta ,\delta ']=\delta \circ \delta '-\delta '\circ \delta \qquad \forall \delta ,\delta '\in {\mathfrak {der}}({\mathfrak {g}})}](//wikimedia.org/api/rest_v1/media/math/render/svg/7e0eb6813db3fcadf440b57bea7cf7aef6168905)
이는  의 부분 리 대수를 이룬다. 만약
의 부분 리 대수를 이룬다. 만약  가 아벨 리 대수라면
가 아벨 리 대수라면  이다.
이다.
 일 경우,
일 경우,  는 리 대수의 (리 군인) 자기 동형군
는 리 대수의 (리 군인) 자기 동형군  의 리 대수와 같다. 즉, 리 대수의 미분은 무한소 자기 동형으로 생각할 수 있다.
의 리 대수와 같다. 즉, 리 대수의 미분은 무한소 자기 동형으로 생각할 수 있다.
임의의 원소  에 대하여, 딸림표현
에 대하여, 딸림표현 ![{\displaystyle \operatorname {ad} _{x}\colon y\mapsto [x,y]}](//wikimedia.org/api/rest_v1/media/math/render/svg/3b2e1dda362d917bb44eebb7b4c77bdf36bb96a2) 는 미분을 이룬다. 이러한 미분을 내부 미분(內部微分, 영어: inner derivation)이라고 한다.
는 미분을 이룬다. 이러한 미분을 내부 미분(內部微分, 영어: inner derivation)이라고 한다.
우선 다음 성질을 정의하자.
- 아벨 리 대수(Abel Lie代數, 영어: Abelian Lie algebra)는 임의의
 에 대하여
에 대하여 ![{\displaystyle [x,y]=0}](//wikimedia.org/api/rest_v1/media/math/render/svg/0bb3ac5611c95c794cec85401f417c5e0146185d) 인 대수다.
인 대수다.
- 멱영 리 대수는 다음을 만족한다.
 이고,
이고, ![{\displaystyle {\mathfrak {g}}_{k+1}=[{\mathfrak {g}}_{k},{\mathfrak {g}}]}](//wikimedia.org/api/rest_v1/media/math/render/svg/c9da38133e7755ae34ce48fef9871025007703e2) 로 정의하자. 그렇다면
로 정의하자. 그렇다면  인
인  이 존재한다.
이 존재한다.
- 가해 리 대수는 다음을 만족한다.
 이고,
이고, ![{\displaystyle {\mathfrak {g}}_{k+1}=[{\mathfrak {g}}_{k},{\mathfrak {g}}_{k}]}](//wikimedia.org/api/rest_v1/media/math/render/svg/b9c981ca41abced6eb4a99de2d8efc429f83e498) 로 정의하자. 그렇다면
로 정의하자. 그렇다면  인
인  이 존재한다.
이 존재한다.
- 단순 리 대수는 자신이나 0이 아닌 리 대수 아이디얼을 가지지 않고, 가환하지 않는 리 대수다.
- 반단순 리 대수는 0이 아닌 가환 리 대수 아이디얼을 지니지 않는 리 대수다.
다음과 같은 포함 관계가 성립한다.
- 아벨 리 대수 ⊊ 멱영 리 대수 ⊊ 가해 리 대수 ⊊ 리 대수
- 단순 리 대수 ⊊ 반단순 리 대수 ⊊ 리 대수
다음을 보일 수 있다.
- 임의의 유한 차원 실수 또는 복소 리 대수는 행렬로 충실히 표현할 수 있다. (아도 정리 영어: Ado’s theorem)[1][2]
- 임의의 유한 차원 실수 리 대수는 가해 아이디얼과 반단순 부분 리 대수의 반직접합으로 나타낼 수 있다. (레비 분해 영어: Levi decomposition)[3]
- (실수 또는 복소수) 콤팩트 리 군의 리 대수는 반단순 리 대수와 아벨 리 대수의 직합이다. (이를 간혹 콤팩트 리 대수라 부르기도 한다. 물론, 리 대수는 벡터 공간이므로 위상수학적으로 절대 콤팩트 공간이 아니다.)
- 모든 반단순 리 대수는 단순 리 대수의 직합으로 유일하게 나타낼 수 있다.
아벨 리 대수는 자명하게 차원으로 분류된다. 실수와 복소수 단순 리 대수는 완전히 분류되었다. 복소수 단순 리 대수는 4개의 무한한 족과 5개의 예외적 대수로 분류되며, 주어진 복소수 단순 리 대수에 대응되는 (유한한 수의) 실수 단순 리 대수 역시 완전히 알려져 있다. 그러나 가해 리 대수의 분류는 매우 어렵다.
3차원 이하의 실수 리 대수에 대하여, 비앙키 분류(영어: Bianchi classification)라는 분류가 존재한다.[4][5] 이는 루이지 비앙키가 도입하였다.
3차원 실수 리 대수
모든 3차원 실수 리 대수는 단순 리 대수이거나 가해 리 대수이다. 3차원 단순 리 대수는
실수 반단순 리 대수는  와
와  두 개가 있다. 전통적으로
두 개가 있다. 전통적으로  는 VIII형,
는 VIII형,  는 IX형으로 불린다.
는 IX형으로 불린다.
3차원 실수 가해 리 대수는 아벨 리 대수의 반직접합  으로 나타낼 수 있다. 이 경우, 작용
으로 나타낼 수 있다. 이 경우, 작용


는 2×2 실수 정사각 행렬  에 의하여 완전히 결정된다.
에 의하여 완전히 결정된다.  과
과  (
( ,
,  )는 동형인 반직접합을 결정하므로, 이러한 리 대수의 분류는 2×2 실수 정사각 행렬의 닮음 분류로 귀결된다. 이는 다음과 같이
)는 동형인 반직접합을 결정하므로, 이러한 리 대수의 분류는 2×2 실수 정사각 행렬의 닮음 분류로 귀결된다. 이는 다음과 같이  의 조르당 표준형으로 결정되며, 이들에는 전통적으로 I형~VII형으로의 이름이 붙어 있다.
의 조르당 표준형으로 결정되며, 이들에는 전통적으로 I형~VII형으로의 이름이 붙어 있다.

이 가운데 I형은 아벨 리 대수이며, II형은 하이젠베르크 대수  이자 2차원 갈릴레이 대수
이자 2차원 갈릴레이 대수  이다. 이 둘은 위 분류 가운데 유일한 멱영 리 대수들이다. III형은 직합
이다. 이 둘은 위 분류 가운데 유일한 멱영 리 대수들이다. III형은 직합  와 같다. V형은 평면의 닮음 변환군(영어: homothety, 평행 이동과 확대 변환으로 생성되는 군)의 리 대수
와 같다. V형은 평면의 닮음 변환군(영어: homothety, 평행 이동과 확대 변환으로 생성되는 군)의 리 대수  이며, VI0형은 (1,1)차원 푸앵카레 대수
이며, VI0형은 (1,1)차원 푸앵카레 대수  와 같으며, VII0형은 2차원 유클리드 대수
와 같으며, VII0형은 2차원 유클리드 대수  와 같다. II형과 VI0형은 3차원 다양체의 기하화 추측의 8가지 기하 가운데 각각 영기하와 해기하에 대응한다. VI형과 VII형은 무한한 족을 이루며, 나머지는 모두 (동형 아래) 하나의 리 대수에 대응한다.
와 같다. II형과 VI0형은 3차원 다양체의 기하화 추측의 8가지 기하 가운데 각각 영기하와 해기하에 대응한다. VI형과 VII형은 무한한 족을 이루며, 나머지는 모두 (동형 아래) 하나의 리 대수에 대응한다.
즉,

일 경우,  로 잡으면 그 리 괄호는 구체적으로 다음과 같다.
로 잡으면 그 리 괄호는 구체적으로 다음과 같다.
![{\displaystyle [t,x]=ax}](//wikimedia.org/api/rest_v1/media/math/render/svg/d03be7d99201e4cf9b39e2dbdab1efbd05b8c4d7)
![{\displaystyle [t,y]=t(bx+cy)}](//wikimedia.org/api/rest_v1/media/math/render/svg/39821d64472f7d8b62198c09d4cf2502977ed276)
3차원 복소수 리 대수
3차원의 복소수 리 대수의 비앙키 분류는 실수의 경우와 유사하지만, 대수적으로 닫힌 체이므로 더 간단하다.
3차원 복소수 단순 리 대수의 경우,  하나밖에 없다. 이는 전통적으로 VIII/IX형으로 불린다.
하나밖에 없다. 이는 전통적으로 VIII/IX형으로 불린다.
3차원 복소수 가해 리 대수의 경우, 마찬가지로 2×2 복소수 행렬의 조르당 표준형의 분류로 귀결되는데, 이 경우 VI형과 VII형이 같아지며, VI0형과 VII0 형이 같아진다.

벡터장
매끄러운 다양체  위의 매끄러운 벡터장들의 벡터 공간
위의 매끄러운 벡터장들의 벡터 공간  은 리 미분에 대하여 리 대수를 이룬다.
은 리 미분에 대하여 리 대수를 이룬다.
리 군  위의, 왼쪽 불변 벡터장들은 리 대수
위의, 왼쪽 불변 벡터장들은 리 대수  를 이룬다. 즉,
를 이룬다. 즉,  는
는  의 부분 리 대수로 생각할 수 있다.
의 부분 리 대수로 생각할 수 있다.
심플렉틱 다양체  위의 매끄러운 함수
위의 매끄러운 함수  에 대하여, 다음과 같이 푸아송 괄호를 정의하자.
에 대하여, 다음과 같이 푸아송 괄호를 정의하자.

그렇다면 이는 야코비 항등식을 만족시키며, 따라서  는
는  -리 대수를 이룬다.
-리 대수를 이룬다.  의 꼴로 나타내어지는 벡터장을 해밀턴 벡터장이라고 하며, 해밀턴 벡터장의 리 미분은 푸아송 괄호와 일치한다. 즉,
의 꼴로 나타내어지는 벡터장을 해밀턴 벡터장이라고 하며, 해밀턴 벡터장의 리 미분은 푸아송 괄호와 일치한다. 즉,  는 해밀턴 벡터장들로 구성된
는 해밀턴 벡터장들로 구성된  의 부분 리 대수로 생각할 수 있다.
의 부분 리 대수로 생각할 수 있다.
보다 일반적으로, 푸아송 다양체  가 주어졌을 때,
가 주어졌을 때,  는
는  -리 대수를 이룬다.
-리 대수를 이룬다.
형식적 벡터장
표수가 0인 체  위의 형식적 멱급수환
위의 형식적 멱급수환 ![{\displaystyle K[[x_{1},\dots ,x_{n}]]}](//wikimedia.org/api/rest_v1/media/math/render/svg/21593c56ca19a77ee8671b2de4c853eb0cd2f8f6) 을 생각하자. 이 가환환 위의 미분은
을 생각하자. 이 가환환 위의 미분은  차원 공간 위의 형식적 벡터장으로 생각할 수 있다. 이러한 모든 미분들의 집합
차원 공간 위의 형식적 벡터장으로 생각할 수 있다. 이러한 모든 미분들의 집합 ![{\displaystyle \operatorname {Der} K[[x_{1},\dots ,x_{n}]]}](//wikimedia.org/api/rest_v1/media/math/render/svg/3f08360c4276aea9d096a6adb956b2fca62c4f13) 은 리 대수를 이룬다.
은 리 대수를 이룬다. ![{\displaystyle \operatorname {Der} K[[x_{1},\dots ,x_{n}]]}](//wikimedia.org/api/rest_v1/media/math/render/svg/3f08360c4276aea9d096a6adb956b2fca62c4f13) 의 부분 리 대수를 형식적 벡터장 리 대수(영어: Lie algebra of formal vector fields)라고 한다.[9]
의 부분 리 대수를 형식적 벡터장 리 대수(영어: Lie algebra of formal vector fields)라고 한다.[9]
두 형식적 벡터장 리 대수 ![{\displaystyle {\mathfrak {g}}\subseteq \operatorname {Der} K[[x_{1},\dots ,x_{n}]]}](//wikimedia.org/api/rest_v1/media/math/render/svg/89eaac1e11da488e21d4cd76462d8bacff2d982e) 가
가 ![{\displaystyle K[[x_{1},\dots ,x_{n}]]}](//wikimedia.org/api/rest_v1/media/math/render/svg/21593c56ca19a77ee8671b2de4c853eb0cd2f8f6) 의 자기 동형을 통해 관련된다면, 서로 좌표 변환 아래 동치(영어: equivalent under coordinate transformation)라고 한다.
의 자기 동형을 통해 관련된다면, 서로 좌표 변환 아래 동치(영어: equivalent under coordinate transformation)라고 한다.
![{\displaystyle X\in \operatorname {Der} K[[x_{1},\dots ,x_{n}]]}](//wikimedia.org/api/rest_v1/media/math/render/svg/b17267cf75c438b353abd26ead4a6d1a2cfecbea) 의 차수는 다음과 같다.
의 차수는 다음과 같다.

여기서 우변에서  이다. 이렇게 형식적 벡터장의 차수를 정의한다면,
이다. 이렇게 형식적 벡터장의 차수를 정의한다면, ![{\displaystyle \operatorname {ord} [X,Y]\geq \operatorname {ord} X+\operatorname {ord} Y}](//wikimedia.org/api/rest_v1/media/math/render/svg/c09fccb06faf33a0ffb181add26a34e67bec0ba8) 가 된다. 따라서, 형식적 벡터장 리 대수
가 된다. 따라서, 형식적 벡터장 리 대수  속에서, 차수가 0 이상인 원소들의 부분 벡터 공간
속에서, 차수가 0 이상인 원소들의 부분 벡터 공간  는 부분 리 대수를 이룬다.
는 부분 리 대수를 이룬다.  의
의  속의 여차원은
속의 여차원은  이하이다. 만약
이하이다. 만약  의 여차원이
의 여차원이  이라면,
이라면,  을 추이적 형식적 벡터장 리 대수(영어: transitive Lie algebra of formal vector fields)라고 한다.
을 추이적 형식적 벡터장 리 대수(영어: transitive Lie algebra of formal vector fields)라고 한다.
1차원 공간 위의 유한 차원 형식적 벡터장 리 대수는 모두 분류되었으며, 다음과 같이 두 개의 무한 족과 하나의 예외가 있다.
 ,
,  . 이는 1차원 아벨 리 대수이다.
. 이는 1차원 아벨 리 대수이다. ,
,  . 이는 2차원 비아벨 가해 리 대수이다.
. 이는 2차원 비아벨 가해 리 대수이다. . 이는 3차원 단순 리 대수이며, 2차원 특수 선형 대수
. 이는 3차원 단순 리 대수이며, 2차원 특수 선형 대수  와 동형이다.
와 동형이다.
이 가운데 추이적 형식적 벡터장 리 대수는  ,
,  ,
,  세 개이다.
세 개이다.
대수적으로 닫힌 체 계수의 2차원 공간 위의 유한 차원 추이적 형식적 벡터장 리 대수들은 소푸스 리가 분류하였다.[9] 실수체의 경우에도 마찬가지로 유사한 분류가 존재한다.[10]
반단순 리 대수
표수 0인 대수적으로 닫힌 체  위의 반단순 리 대수는 모두 분류되었다. 반단순 리 대수는 단순 리 대수들의 직합이며, 단순 리 대수는
위의 반단순 리 대수는 모두 분류되었다. 반단순 리 대수는 단순 리 대수들의 직합이며, 단순 리 대수는  ,
,  ,
,  ,
,  4개의 무한 족과
4개의 무한 족과  ,
,  ,
,  ,
,  ,
,  5개의 예외 단순 리 대수로 분류된다.
5개의 예외 단순 리 대수로 분류된다.
표수 0인 대수적으로 닫힌 체  위의 반단순 리 대수
위의 반단순 리 대수  속에 카르탕 부분 대수
속에 카르탕 부분 대수  를 잡자. 그렇다면,
를 잡자. 그렇다면,  속의
속의  의 근계
의 근계  를 생각하자. 그렇다면, 단순 리 대수의 구조론에 따라
를 생각하자. 그렇다면, 단순 리 대수의 구조론에 따라  는
는  -등급 리 대수를 이룬다. 구체적으로,
-등급 리 대수를 이룬다. 구체적으로,  의 등급은
의 등급은
![{\displaystyle (\deg g)h=[h,g]}](//wikimedia.org/api/rest_v1/media/math/render/svg/912e70ba1cfefe3ab325e3b9b2ad4c941656f52d)
이다.
중심렬
군  속의 한 중심렬
속의 한 중심렬

이 주어졌다고 하자. 즉, 모든  에 대하여
에 대하여
![{\displaystyle [G_{i},G_{j}]\leq G_{i+j}}](//wikimedia.org/api/rest_v1/media/math/render/svg/21b45fc23fb4cfa7c628c686e147b0a259fdf30d)
라고 하자. 그렇다면,  은 모두 아벨 군을 이룬다. 이 몫군들의 직합을 생각하자.
은 모두 아벨 군을 이룬다. 이 몫군들의 직합을 생각하자.

이는 자연스럽게 아벨 군을 이룬다. 이 위에 다음과 같이 리 괄호를 군 교환자로 정의하자.
![{\displaystyle [xG_{i},yG_{j}]=x^{-1}y^{-1}xyG_{i+j}}](//wikimedia.org/api/rest_v1/media/math/render/svg/bc446f2b7cbbede0a8ed8be9565e1b6c85575820)
그렇다면, 이는 자연수 등급이 붙은 등급 리 환을 이룬다.
호모토피 군
점을 가진 공간  위의 호모토피 군
위의 호모토피 군  위에는 화이트헤드 괄호라는 다음과 같은 쌍선형 이항 연산이 존재한다.
위에는 화이트헤드 괄호라는 다음과 같은 쌍선형 이항 연산이 존재한다.
![{\displaystyle [,]\colon \pi _{k}(X)\times \pi _{l}(X)\to \pi _{k+l-1}(X)}](//wikimedia.org/api/rest_v1/media/math/render/svg/aaac5143955ba893ac4797dd747f3298b2332344)
이는 야코비 항등식을 만족시키며, 반대칭이지만, 일반적으로 교대 형식을 이루지 않는다.[11] 만약 여기서 꼬임 부분군에 대한 몫을 취하면 리 대수를 얻는다. 구체적으로, 유리수 호모토피 이론에서 유리수 계수의 호모토피 군

을 생각하면, 이는 화이트헤드 괄호 아래 유리수 계수 등급 리 대수를 이룬다.
소푸스 리가 리 군을 다루기 위하여 도입하였으며, "무한소군"(영어: infinitesimal group)으로 일컬었다. 빌헬름 킬링은 1888년~1890년 동안 반단순 리 대수의 분류를 제창하였고, 1894년에 엘리 카르탕이 킬링의 분류를 엄밀하게 증명하였다.[12] 1898년에 루이지 비앙키는 3차원 이하의 리 대수의 비앙키 분류를 제시하였다.[4]
1930년대에 헤르만 바일이 "리 대수"라는 용어를 도입하였다. 아도 정리는 이고리 드미트리예비치 아도(러시아어: И́горь Дми́триевич Адо́)가 1935년에 증명하였다.[1] 레비 분해 정리는 1950년에 에우제니오 엘리아 레비(이탈리아어: Eugenio Elia Levi)가 증명하였다.[3]

![{\displaystyle ({\mathfrak {g}},[\cdot ,\cdot ])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1acf5360abf7b837b08e1298909959fcd868d061)

![{\displaystyle [\cdot ,\cdot ]:{\mathfrak {g}}\times {\mathfrak {g}}\to {\mathfrak {g}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/44ce0ecebaaa6530dea73faf9e5831dacb050936)


![{\displaystyle [ax+by,z]=a[x,z]+b[y,z],\quad [z,ax+by]=a[z,x]+b[z,y]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/730cd19026c1c8b8b3ac4e918cad74872c023d23)

![{\displaystyle [x,x]=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/94ccb967db9ab0773c5aa2e0fc234cd33373f193)
![{\displaystyle [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/23655a62f2a7cc545f121d9bcc30fe2c56731457)


![{\displaystyle [x,y]+[y,x]=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5ba3f4019700f26de2bd59625e7b078ba3d11929)




![{\displaystyle [{\mathfrak {h}},{\mathfrak {h}}]\subseteq {\mathfrak {h}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6f4986c8b70a0f7c4fe936113e1136032b304158)

![{\displaystyle [{\mathfrak {g}},I]\subseteq I}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7d68863173b4cf90ca34d1868f89c30f1a95aa61)




![{\displaystyle [\cdot ,\cdot ]\colon {\mathfrak {g}}_{d}\times {\mathfrak {g}}_{d'}\to {\mathfrak {g}}_{d+d'}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/22fcdf15d35825f322069e4116ce069db797bd28)



![{\displaystyle [-,-]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7ba9b4dfaeae181a7a507d66e1b54fb640a7c61d)
![{\displaystyle [x,y]=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0bb3ac5611c95c794cec85401f417c5e0146185d)
















![{\displaystyle \operatorname {Z} ({\mathfrak {g}})=\{x\in {\mathfrak {g}}\colon [x,{\mathfrak {g}}]=0\}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e953afc610a77831aae97c8e07c3b89076b23f0a)


![{\displaystyle [x+{\mathfrak {a}},y+{\mathfrak {a}}]=[x,y]+{\mathfrak {a}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a07bc6fdc5136397613a0ce5e2b3237d390db524)

![{\displaystyle [g,g']_{{\mathfrak {g}}\oplus {\mathfrak {h}}}=[g,g']_{\mathfrak {g}}\qquad \forall g,g'\in {\mathfrak {g}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/207a589efa7b9e8cbafd94a60ed30877769809a1)
![{\displaystyle [h,h']_{{\mathfrak {g}}\oplus {\mathfrak {h}}}=[h,h']_{\mathfrak {h}}\qquad \forall h,h'\in {\mathfrak {h}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7788fc94350b6492e43f82b0e6a44f5ab2a5f93d)
![{\displaystyle [g,h]_{{\mathfrak {g}}\oplus {\mathfrak {h}}}=[h,g]_{{\mathfrak {g}}\oplus {\mathfrak {h}}}=0\qquad \forall g\in {\mathfrak {g}},\;h\in {\mathfrak {h}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7b6814ac937b269176f7d9ab06fc873e59aec12a)







![{\displaystyle \delta [x,y]=[\delta x,y]+[x,\delta y]\qquad \forall x,y\in {\mathfrak {g}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/10ce0eb2ed31d1e4cf0364deca1d6fcb73052f1d)

![{\displaystyle [\delta ,\delta ']=\delta \circ \delta '-\delta '\circ \delta \qquad \forall \delta ,\delta '\in {\mathfrak {der}}({\mathfrak {g}})}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7e0eb6813db3fcadf440b57bea7cf7aef6168905)




![{\displaystyle \operatorname {ad} _{x}\colon y\mapsto [x,y]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3b2e1dda362d917bb44eebb7b4c77bdf36bb96a2)

![{\displaystyle {\mathfrak {g}}_{k+1}=[{\mathfrak {g}}_{k},{\mathfrak {g}}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/c9da38133e7755ae34ce48fef9871025007703e2)


![{\displaystyle {\mathfrak {g}}_{k+1}=[{\mathfrak {g}}_{k},{\mathfrak {g}}_{k}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b9c981ca41abced6eb4a99de2d8efc429f83e498)



























![{\displaystyle [t,x]=ax}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d03be7d99201e4cf9b39e2dbdab1efbd05b8c4d7)
![{\displaystyle [t,y]=t(bx+cy)}](http://wikimedia.org/api/rest_v1/media/math/render/svg/39821d64472f7d8b62198c09d4cf2502977ed276)
 ...
...












![{\displaystyle [0,0]=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/45c2f037157e1e266f310c16432c8d245a58408c)

![{\displaystyle [a,b]=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/67fe10397a99e43e831508fe1293862ec0a9cca3)


![{\displaystyle [a,b]=a\cdot b-b\cdot a}](http://wikimedia.org/api/rest_v1/media/math/render/svg/09dc91e5156b387e1860815c707cff9cb9a03662)



![{\displaystyle [\delta ,\delta ']=\delta \circ \delta '-\delta '\circ \delta }](http://wikimedia.org/api/rest_v1/media/math/render/svg/4959f80b5b52f35610b4a3a399e8644a2d327e36)
![{\displaystyle [\delta ,\delta ']}](http://wikimedia.org/api/rest_v1/media/math/render/svg/33f80183ea05a04b99576dd8b57e3e7693fdfc16)














![{\displaystyle K[[x_{1},\dots ,x_{n}]]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/21593c56ca19a77ee8671b2de4c853eb0cd2f8f6)

![{\displaystyle \operatorname {Der} K[[x_{1},\dots ,x_{n}]]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3f08360c4276aea9d096a6adb956b2fca62c4f13)
![{\displaystyle {\mathfrak {g}}\subseteq \operatorname {Der} K[[x_{1},\dots ,x_{n}]]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/89eaac1e11da488e21d4cd76462d8bacff2d982e)
![{\displaystyle X\in \operatorname {Der} K[[x_{1},\dots ,x_{n}]]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b17267cf75c438b353abd26ead4a6d1a2cfecbea)


![{\displaystyle \operatorname {ord} [X,Y]\geq \operatorname {ord} X+\operatorname {ord} Y}](http://wikimedia.org/api/rest_v1/media/math/render/svg/c09fccb06faf33a0ffb181add26a34e67bec0ba8)


























![{\displaystyle (\deg g)h=[h,g]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/912e70ba1cfefe3ab325e3b9b2ad4c941656f52d)


![{\displaystyle [G_{i},G_{j}]\leq G_{i+j}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/21b45fc23fb4cfa7c628c686e147b0a259fdf30d)


![{\displaystyle [xG_{i},yG_{j}]=x^{-1}y^{-1}xyG_{i+j}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/bc446f2b7cbbede0a8ed8be9565e1b6c85575820)


![{\displaystyle [,]\colon \pi _{k}(X)\times \pi _{l}(X)\to \pi _{k+l-1}(X)}](http://wikimedia.org/api/rest_v1/media/math/render/svg/aaac5143955ba893ac4797dd747f3298b2332344)