환 (수학)

추상대수학에서 환(環, 영어: ring)은 덧셈과 곱셈이 정의된 대수 구조의 하나이다. 환은 덧셈에 대하여 아벨 군을 이루고, 분배법칙과 곱셈의 결합법칙 및 항등원의 존재를 만족시키지만, 곱셈에 대한 역원은 존재하지 않을 수 있다. 환을 연구하는 추상대수학의 분야를 환론(環論, 영어: ring theory)이라고 한다.

가환환(곱셈의 교환법칙이 성립하는 환)은 비가환환보다 훨씬 많은 성질이 알려져 있으며, 이들의 연구를 가환대수학이라고 한다. 가환대수학은 대수기하학 및 대수적 수론과 깊은 관련이 있다. 1980년대 이후에는 비가환 기하학과 양자군 등의 이론이 나타나면서 비가환환에 대해서도 상당한 연구가 이루어지고 있다.

환에 대한 관련된 개념으로, 군의 표현(혹은 가군)이나 군환, 나눗셈환, 보편 포락 대수 등의 특수한 환 및 인접 분야인 호몰로지 대수학 등이 있다.

정의

환론을 창시한 수학자 중 한 명인 리하르트 데데킨트

환은 아벨 군과 모노이드의 구조를 동시에 갖고, 두 구조가 서로 호환되는 대수 구조이다. 구체적으로, 환 ${\displaystyle (R,+,\cdot )}$은 이항 연산

${\displaystyle +\colon R\times R\to R}$

${\displaystyle \cdot \colon R\times R\to R}$

을 갖추고, 다음 공리들을 만족시키는 집합이다.^{[1]:83[2]:136}

• ${\displaystyle (R,+)}$는 아벨 군을 이룬다. 즉, 구체적으로 다음이 성립한다.
  • (덧셈 결합 법칙) 임의의 ${\displaystyle r,s,t\in R}$에 대하여, ${\displaystyle (r+s)+t=r+(s+t)}$
  • (덧셈 교환 법칙) 임의의 ${\displaystyle r,s\in R}$에 대하여,${\displaystyle r+s=s+r}$
  • (덧셈 항등원의 존재) 임의의 ${\displaystyle r\in R}$에 대하여 ${\displaystyle 0_{R}+r=r}$인 원소 ${\displaystyle 0_{R}\in R}$가 존재한다.
  • (덧셈 역원의 존재) 임의의 ${\displaystyle r\in R}$에 대하여, ${\displaystyle r+(-r)=0_{R}}$인 원소 ${\displaystyle -r\in R}$가 존재한다.
• ${\displaystyle (R,\cdot )}$은 모노이드를 이룬다. 즉, 구체적으로 다음이 성립한다.
  • (곱셈 결합 법칙) 임의의 ${\displaystyle r,s,t\in R}$에 대하여, ${\displaystyle (rs)t=r(st)}$
  • (곱셈 항등원의 존재) 임의의 ${\displaystyle r\in R}$에 대하여 ${\displaystyle r1_{R}=r}$인 원소 ${\displaystyle 1_{R}\in R}$이 존재한다.
• 덧셈과 곱셈 사이에는 분배 법칙이 성립한다. 즉, 다음 두 조건이 성립한다.
  • (오른쪽 분배 법칙) 임의의 ${\displaystyle r,s,t\in R}$에 대하여, ${\displaystyle r(s+t)=rs+rt}$
  • (왼쪽 분배 법칙) 임의의 ${\displaystyle r,s,t\in R}$에 대하여, ${\displaystyle (s+t)r=sr+tr}$

환의 개념은 다음과 같이 다르게 정의할 수 있으나, 이들 정의들은 모두 서로 동치이다.

• 환은 정수환 ${\displaystyle \mathbb {Z} }$ 위의 단위 결합 대수이다.
• 아벨 군의 범주 ${\displaystyle \operatorname {Ab} }$는 텐서곱에 대하여 모노이드 범주를 이룬다. 범주론적으로, 환은 아벨 군의 모노이드 범주에서의 모노이드 대상이다.
• 환은 아벨 군의 모노이드 범주에 대하여 풍성한 범주 가운데, 하나의 대상을 갖는 것이다. 이 경우, 환의 원소들은 범주의 유일한 원소의 자기 사상들이다.

환의 개념은 다음과 같은 개념들과 유사하지만 다른 개념이다.

• 일반적인 환에서는 곱셈 교환 법칙이 성립하지 않는다. 이 조건을 추가하면, 가환환의 개념을 얻는다.
• 일반적인 환에서는 원소의 곱셈에 대한 역원이 존재하지 않을 수 있다. 0이 아닌 모든 원소가 가역원이라는 조건을 추가하면, 나눗셈환의 개념을 얻는다.
• 일반적인 환에서는 항상 곱셈 항등원이 존재해야 한다. 이 조건을 생략하면, 유사환이라는 개념을 얻는다. (일부 저자들은 모든 유사환을 "환"이라고 부르기도 한다.^{[3]:223[4]:105})

환 준동형

두 환 ${\displaystyle R}$, ${\displaystyle S}$ 사이의 함수 ${\displaystyle f\colon R\to S}$가 다음 두 조건들을 만족시킨다면, 환 준동형 사상(環準同型寫像, 영어: ring homomorphism)이라고 한다.

• ${\displaystyle f}$는 덧셈 군 준동형이다. 즉, 임의의 ${\displaystyle r,s\in R}$에 대하여, ${\displaystyle f(r+s)=f(r)+f(s)}$이다.
• ${\displaystyle f}$는 곱셈 모노이드 준동형이다. 즉, 임의의 ${\displaystyle r,s\in R}$에 대하여 ${\displaystyle f(rs)=f(r)f(s)}$이며, ${\displaystyle f(1)=1}$이다.

유사환의 준동형은 ${\displaystyle f(1)=1}$일 필요가 없다. 따라서, 모든 환 준동형은 유사환 준동형이지만, 그 역은 일반적으로 성립하지 않는다.

부분환

환의 부분 집합 ${\displaystyle S\subseteq R}$이 다음 두 조건을 만족시킨다면, 부분환(部分環, 영어: subring)이라고 한다.

• ${\displaystyle S}$는 덧셈 부분군을 이룬다. 즉, 다음이 성립한다.
  • 임의의 ${\displaystyle s,s'\in S}$에 대하여, ${\displaystyle s+s'\in S}$
  • 임의의 ${\displaystyle s\in S}$에 대하여, ${\displaystyle -s\in S}$
• ${\displaystyle S}$는 곱셈 부분 모노이드를 이룬다. 즉, 다음이 성립한다.
  • ${\displaystyle 1_{R}\in S}$
  • 임의의 ${\displaystyle s,s'\in S}$에 대하여, ${\displaystyle ss'\in S}$

즉, 부분환은 덧셈 부분군이자 곱셈 부분 모노이드인 부분 집합이다.

아이디얼은 전체 아이디얼이 아닐 경우 1을 포함하지 않으므로 부분환이 될 수 없다.

가군과 아이디얼

 이 부분의 본문은 가군입니다.

 이 부분의 본문은 아이디얼입니다.

환의 특정 부분 집합을 아이디얼이라고 한다. 환 ${\displaystyle R}$의 아이디얼 ${\displaystyle {\mathfrak {a}}\subseteq R}$이 주어지면, 이에 대한 몫환 ${\displaystyle R/{\mathfrak {a}}}$을 정의할 수 있다. 이는 군과 그 정규 부분군이 주어졌을 때, 몫군을 취할 수 있는 것과 마찬가지다.

군이나 모노이드가 집합 위에 왼쪽·오른쪽에서 작용할 수 있는 것처럼, 환의 경우 아벨 군 위에 왼쪽·오른쪽으로 작용할 수 있다. 이렇게 환의 (왼쪽·오른쪽) 작용을 갖춘 아벨 군을 왼쪽·오른쪽 가군이라고 한다. 왼쪽·오른쪽 아이디얼은 왼쪽·오른쪽 가군의 특수한 경우이다. 대략, 군의 작용과 환의 작용에 대하여 다음과 같이 대응되는 개념들이 존재한다.

군론	환론
군	환
군의 왼쪽·오른쪽 작용	왼쪽·오른쪽 가군
부분군	부분환
정규 부분군	양쪽 아이디얼
몫군	몫환
추이적 작용	순환 가군
안정자군	소멸자
충실한 작용	충실한 가군

연산

주어진 환들로부터 새로운 환을 만드는 다양한 연산들이 존재한다.

반대환

환 ${\displaystyle (R,+,\cdot )}$이 주어졌을 때, 그 위에 다음과 같은 새로운 곱셈 연산을 주자.

${\displaystyle r\cdot 's=s\cdot r\qquad \forall r,s\in R}$

그렇다면 ${\displaystyle (R,+,\cdot ')}$은 환을 이루며, 이를 ${\displaystyle R}$의 반대환(反對環, 영어: opposite ring) ${\displaystyle R^{\operatorname {op} }}$이라고 한다. 즉, ${\displaystyle R^{\operatorname {op} }}$는 덧셈 아벨 군으로서 ${\displaystyle R}$와 같지만, 곱셈 모노이드로서 ${\displaystyle R}$의 반대 모노이드이다.

환을 하나의 대상을 갖는, 아벨 군의 모노이드 범주 위의 풍성한 범주로 생각하였을 때, 이는 반대 범주의 특수한 경우이다.

몫환

군론의 몫군이나 선형대수학의 몫공간과 마찬가지로, 환론에서도 몫환(-環, 영어: quotient ring)의 개념을 정의할 수 있다. 환론에서 정규 부분군에 해당하는 대상은 양쪽 아이디얼이며, 이에 대한 몫환은 대략 아이디얼에 속한 원소를 모두 0으로 간주하여 얻는 환이다.

환 ${\displaystyle R}$ 및 그 속의 양쪽 아이디얼 ${\displaystyle {\mathfrak {a}}}$이 주어졌다고 하자. 그렇다면, ${\displaystyle R}$ 위에 다음과 같은 동치 관계 ${\displaystyle \sim }$를 정의할 수 있다.

${\displaystyle r\sim s\iff r-s\in {\mathfrak {a}}\qquad \forall r,s\in R}$

이 동치 관계에 대한 동치류는 다음과 같다.

${\displaystyle [r]_{\sim }=r+{\mathfrak {a}}=\{r+a\colon a\in {\mathfrak {a}}\}}$

${\displaystyle R/{\mathfrak {a}}}$는 이러한 동치류들의 집합이다. 그 위의 환의 연산은 다음과 같다.

${\displaystyle (r+{\mathfrak {a}})+(s+{\mathfrak {a}})=(r+s)+{\mathfrak {a}}}$

${\displaystyle (r+{\mathfrak {a}})(s+{\mathfrak {a}})=rs+{\mathfrak {a}}}$

이 연산들은 동치류의 대표원의 선택에 의존하지 않는다는 것을 아이디얼의 정의에 따라 쉽게 확인할 수 있다. 몫환에서는 ${\displaystyle 0_{R/{\mathfrak {a}}}=0+{\mathfrak {a}}}$이며, ${\displaystyle 1_{R/{\mathfrak {a}}}=1+{\mathfrak {a}}}$이다.

몫환에 대하여, 표준적인 전사 환 준동형

${\displaystyle R\twoheadrightarrow R/{\mathfrak {a}}}$

${\displaystyle r\mapsto r+{\mathfrak {a}}}$

이 존재한다.

직접곱

 이 부분의 본문은 직접곱입니다.

환의 모임은 대수 구조 다양체이므로, 환들의 집합의 직접곱을 정의할 수 있다. 이는 환의 범주의 범주론적 곱을 이룬다. 이는 덧셈 아벨 군으로서는 아벨 군들의 직접곱이며, 곱셈 모노이드로서는 모노이드들의 직접곱이다.

자유곱

 이 부분의 본문은 자유곱입니다.

환의 모임은 대수 구조 다양체이므로, 환들의 집합의 자유곱을 정의할 수 있다. 이는 환의 범주의 쌍대곱을 이룬다. 일반적으로, 환들의 자유곱은 매우 복잡하다.

다항식환

 이 부분의 본문은 다항식환입니다.

 이 부분의 본문은 텐서 대수입니다.

환 ${\displaystyle R}$ 및 집합 ${\displaystyle X=\{x_{i}\}_{i\in I}}$이 주어졌을 때, ${\displaystyle x_{i}}$들을 ${\displaystyle R}$에 형식적 가환 변수로 간주하여 추가할 수 있다. 이렇게 하여 얻는 환 ${\displaystyle R[X]}$를 ${\displaystyle R}$ 위의 다항식환(영어: polynomial ring)이라고 한다. 만약 ${\displaystyle R}$가 가환환이라면 ${\displaystyle R[X]}$ 역시 가환환이다.

환 ${\displaystyle R}$ 및 집합 ${\displaystyle X=\{x_{i}\}_{i\in I}}$이 주어졌을 때, ${\displaystyle x_{i}}$들을 ${\displaystyle R}$에 가환하지 않는 형식적 변수로 간주하여 추가할 수도 있다. 이렇게 하여 얻는 환 ${\displaystyle R\langle X\rangle }$를 ${\displaystyle R}$ 위의 비가환 다항식환(영어: noncommutative polynomial ring)이라고 한다. 이는 ${\displaystyle R}$가 가환환이더라도 (${\displaystyle X}$가 공집합이 아니고, ${\displaystyle R}$가 자명환이 아니라면) 항상 가환환이 아니다.

성질

기초적 성질

환 ${\displaystyle R}$의 임의의 원소 ${\displaystyle r,s,t\in R}$에 대하여, 다음이 성립한다. 여기서 ${\displaystyle 0,1\in R}$는 환의 덧셈 및 곱셈 항등원이다.

• ${\displaystyle 0r=r0=0}$.
  • 증명: 이는 ${\displaystyle 0r=0r+0(r-r)=(0+0)r-0r=0r-0r=0}$이며, 마찬가지로 ${\displaystyle r0=r0+(r-r)0=r(0+0)-r0=r0-r0=0}$이기 때문이다.
• ${\displaystyle (-1)r=r(-1)=-r}$
  • 증명: ${\displaystyle r+(-1)r=1r+(-1)r=(1-1)r=0}$이므로, 덧셈 역원의 정의에 따라 ${\displaystyle (-1)r=-r}$이다. ${\displaystyle r(-1)=-r}$도 마찬가지다.
• ${\displaystyle (-r)s=r(-s)=-(rs)=(-1)rs}$. 이는 위 성질과 곱셈의 결합 법칙으로부터 자명하다.
• 만약 ${\displaystyle r}$와 ${\displaystyle s}$가 가역원이라면, ${\displaystyle rs}$ 역시 가역원이며, 그 역원은 ${\displaystyle (rs)^{-1}=s^{-1}r^{-1}}$이다. 따라서 가역원들의 집합은 가역원군이라는 군을 이룬다.
  • 증명: 결합 법칙에 따라서 ${\displaystyle (rs)(s^{-1}r^{-1})=r(ss^{-1})r^{-1}=rr^{-1}=1}$이다. 마찬가지로 ${\displaystyle (s^{-1}r^{-1})(rs)=1}$이다.

환 가운데, ${\displaystyle 0=1}$인 것은 자명환밖에 없다. 이는 임의의 원소 ${\displaystyle r}$에 대하여 ${\displaystyle r=1r=0r=0}$이기 때문에, 원소가 0밖에 없기 때문이다.

환의 경우, 다른 대수 구조와 마찬가지로 준동형 정리와 동형 정리가 성립한다.

범주론적 성질

환과 환 준동형의 범주 ${\displaystyle \operatorname {Ring} }$은 대수 구조 다양체의 범주이므로, 완비 범주이자 쌍대 완비 범주이다. 이 경우, 각종 극한과 쌍대극한은 다음과 같다.

범주론의 개념	환론의 개념
시작 대상	정수환 ${\displaystyle \mathbb {Z} }$
끝 대상	자명환 ${\displaystyle 0}$
곱	직접곱 ${\displaystyle \prod _{i\in I}R_{i}}$
쌍대곱	환의 자유곱
동등자	집합과 함수의 범주에서의 동등자
쌍대동등자	${\displaystyle f,g\colon R\to S}$의 쌍대동등자는 아이디얼 ${\displaystyle (f(r)-g(r)\colon r\in R)\subseteq S}$에 대한 몫환이다.
단사 대상	자명환 ${\displaystyle 0}$
모노이드 대상	가환환
단사 사상	단사 함수인 환 준동형
전사 사상	(복잡함)[5]

특히, 환의 전사 사상은 전사 함수일 필요가 없다. 하지만 반대로 전사 함수인 환 준동형은 항상 환의 전사 사상이다.

함자

환의 범주 ${\displaystyle \operatorname {Ring} }$은 아벨 군의 범주 · 모노이드의 범주 · 집합의 범주로 가는 충실한 망각 함자를 갖는다. 이들은 각각 곱셈과 덧셈을 잊는다.

${\displaystyle A\colon \operatorname {Ring} \to \operatorname {Ab} }$

${\displaystyle M\colon \operatorname {Ring} \to \operatorname {Mon} }$

이 두 함자는 모두 왼쪽 수반 함자를 갖는다.

• ${\displaystyle A}$의 왼쪽 수반 함자는 아벨 군 ${\displaystyle G}$를 (정수환 위의 가군으로 생각하여) 그 텐서 대수 ${\displaystyle \operatorname {T} (G)}$에 대응시킨다.
• ${\displaystyle M}$의 왼쪽 수반 함자는 모노이드 ${\displaystyle M}$을 정수 계수의 모노이드 환 ${\displaystyle \mathbb {Z} [M]}$에 대응시킨다.

이들은 다른 함자와 다음과 같이 합성할 수 있다.

• 군에서 모노이드로 가는 망각 함자 ${\displaystyle F\colon \operatorname {Grp} \to \operatorname {Mon} }$는 왼쪽 및 오른쪽 수반 함자를 가지며, 이 가운데 왼쪽 수반 함자는 모노이드를 그 가역원군으로 대응시킨다. 이를 환에서 모노이드로 가는 망각 함자와 합성하면, 가역원군 함자 ${\displaystyle \operatorname {Unit} \colon \operatorname {Ring} \to \operatorname {Grp} }$를 얻는다. 이는 (정의에 따라) 왼쪽 함자를 가지며, 이는 군 ${\displaystyle G}$를 정수 계수 군환 ${\displaystyle \mathbb {Z} [G]}$에 대응시킨다.
• 아벨 군의 범주와 모노이드의 범주 둘 다 구체적 범주이므로, 집합의 범주로 가는 망각 함자를 얻는다. 이를 합성하면, 환의 범주에서 집합의 범주로 가는 망각 함자 ${\displaystyle \operatorname {Ring} \to \operatorname {Set} }$를 얻어, 환의 범주 역시 구체적 범주를 이룬다. 이 망각 함자의 왼쪽 수반 함자는 집합 ${\displaystyle S}$를 정수 계수 비가환 다항식환 ${\displaystyle \mathbb {Z} \langle S\rangle }$에 대응시킨다. 이는 ${\displaystyle S}$ 위의 자유 아벨 군의 텐서 대수 ${\displaystyle \operatorname {T} (\mathbb {Z} ^{\oplus |S|})}$와 같으며, ${\displaystyle S}$ 위의 자유 모노이드의 정수 계수 모노이드 환과도 같다.

이 밖에도, 환의 범주에서 유사환의 범주로 가는 포함 함자

${\displaystyle \operatorname {Ring} \to \operatorname {Rng} }$

가 존재한다. 이는 충실한 함자이지만 충만한 함자가 아니다. (즉, 유사환의 준동형 가운데 환 준동형이 아닌 것이 존재한다.) 이 포함 함자는 왼쪽 수반 함자

${\displaystyle {\hat {}}\colon \operatorname {Rng} \to \operatorname {Ring} }$

${\displaystyle {\hat {R}}\colon R\mapsto R\oplus \mathbb {Z} }$

를 가지며, 이를 유사환의 단위화라고 한다.

군론적 성질

환 ${\displaystyle R}$가 주어졌을 때, 곱셈 구조를 잊으면 아벨 군을 얻는다. 반대로, 모든 유한 생성 아벨 군 위에는 하나 이상의 환 구조가 존재한다. 구체적으로, 임의의 유한 생성 아벨 군은 유한 개의 소수 거듭제곱 크기의 순환군 및 유한 개의 무한 순환군들의 직합이다.

${\displaystyle \operatorname {Cyc} (\infty )^{\oplus n_{0}}\bigoplus _{i}\operatorname {Cyc} (p_{i}^{n_{i}})}$

이 아벨 군은 다음 환의 덧셈군이다.

${\displaystyle \mathbb {Z} ^{\oplus n_{0}}\bigoplus _{i}\mathbb {Z} /(p_{i}^{n_{i}})}$

환 ${\displaystyle R}$가 주어졌을 때, 환의 여러 성질들은 그 덧셈군만으로 유추할 수 있다. 예를 들어, 환의 표수는 덧셈군만으로 정의가 가능하며, 또한 환의 일부 아이디얼들의 존재 역시 유추할 수 있다.

유한환의 분류에 따라, 순환군 ${\displaystyle \operatorname {Cyc} (n)}$ 위의 가능한 환 구조는 정수환의 몫환 ${\displaystyle \mathbb {Z} /(n)}$밖에 없다. 보다 일반적으로, ${\displaystyle \operatorname {Cyc} (n)}$위의 가능한 유사환 구조들은 ${\displaystyle n}$의 양의 약수들과 일대일 대응하며, ${\displaystyle \operatorname {Cyc} (n)=\langle a|na=0\rangle }$이라고 놓으면 ${\displaystyle k\mid n}$에 대응하는 유사환은 ${\displaystyle a^{2}=ka}$이다.^{[6]:Theorem 1[7]:283}

무한 순환군 ${\displaystyle \operatorname {Cyc} (\infty )}$ 위의 가능한 환 구조는 정수환 ${\displaystyle \mathbb {Z} }$밖에 없다. 보다 일반적으로, ${\displaystyle \mathbb {Z} }$ 위의 가능한 유사환 구조들은 음이 아닌 정수들과 일대일 대응하며, 구체적으로 정수환의 아이디얼 ${\displaystyle (n)\subseteq \mathbb {Z} }$과 동형이다.^{[7]:283, Exercise 68.5}

꼬임 아벨 군 ${\displaystyle G}$에 대하여, 다음 두 조건이 동치이다.^{[7]:290, Proposition 120.8}

• 원소들의 차수가 유계이다. 즉, ${\displaystyle \textstyle \sup _{g\in G}\min\{n\in \mathbb {Z} ^{+}\colon ng=0\}<\infty }$이다.
• ${\displaystyle G}$를 덧셈군으로 하는 환이 적어도 하나 존재한다.

예를 들어, 덧셈군 ${\displaystyle \mathbb {Q} /\mathbb {Z} }$이나 프뤼퍼 군 위에는 환 구조가 존재하지 않는다. 물론, 임의의 아벨 군에 대하여 이를 덧셈군으로 하는 유사환은 항상 존재한다. (아벨 군에 모든 곱이 0인 곱셈을 주면 된다.)

임의의 환 ${\displaystyle R}$에 대하여, 그 가역원군 ${\displaystyle \operatorname {Unit} (R)}$은 군을 이룬다. 반대로, 군 ${\displaystyle G}$에 대하여, 군환 ${\displaystyle \mathbb {Z} [G]}$의 가역원군은 ${\displaystyle G}$를 부분군으로 갖는다.

${\displaystyle G\subseteq \operatorname {Unit} (\mathbb {Z} [G])}$

소수 크기의 유한 순환군 ${\displaystyle \operatorname {Cyc} (p)}$에 대하여 다음 두 조건이 서로 동치이다.^{[7]:323, Exercise 129.4}

• ${\displaystyle p=2}$이거나, ${\displaystyle p=2^{n}-1}$의 꼴이다.
• 가역원군이 ${\displaystyle \operatorname {Cyc} (p)}$인 환이 존재한다.

모형 이론적 성질

환은 다음과 같은 연산들을 갖춘 대수 구조이다.

• 두 개의 이항 연산 (${\displaystyle +}$, ${\displaystyle \cdot )}$
• 한 개의 1항 연산 (${\displaystyle -}$)
• 두 개의 0항 연산 (${\displaystyle 0}$, ${\displaystyle 1}$)

환들의 모임은 대수 구조 다양체를 이룬다. (반면, 예를 들어 체의 모임은 역수 조건이 대수적이지 않으므로 대수 구조 다양체를 이루지 않는다.) 마찬가지로, 다음 모임들은 대수 구조 다양체를 이룬다.

• 소수 ${\displaystyle p}$에 대하여 표수가 ${\displaystyle p}$이거나 아니면 자명환인 환들의 모임
• 양의 정수 ${\displaystyle n}$에 대하여, 표수가 ${\displaystyle n}$의 약수인 환들의 모임
• 가환환들의 모임
• 폰 노이만 정칙환들의 모임

환의 대수 구조 다양체에서, (보편 대수학적) 준동형은 통상적인 환 준동형과 같으며, 부분 대수는 통상적인 부분환과 같으며, 단순 대수는 통상적인 단순환과 같다.

환의 대수 구조 다양체에서, 합동 관계는 양쪽 아이디얼과 같다. 구체적으로, 환 ${\displaystyle R}$의 합동 관계들의 집합과 양쪽 아이디얼들의 집합 사이에는 일대일 대응이 존재하며, 합동 관계 ${\displaystyle \sim }$에 대응하는 아이디얼은 0과 합동인 원소들의 집합 ${\displaystyle \{r\colon r\sim 0\}}$이다.^[8]:39–40

환의 대수 구조 다양체에서, 환 ${\displaystyle R}$의 보편 대수학적 중심은 통상적인 환의 중심이 아니라, 다음과 같은 양쪽 아이디얼이다.^[8]:93

${\displaystyle \{r\in R\colon rR=Rr=\{0\}\}}$

이는 환의 스스로의 왼쪽 가군으로서의 소멸자와 스스로의 오른쪽 가군으로서의 소멸자의 교집합과 같다.

격자 이론적 성질

환 ${\displaystyle R}$에 대하여, 양쪽 아이디얼들의 (포함 관계에 대한) 부분 순서 집합 ${\displaystyle (\operatorname {Ideal} (R),\subseteq )}$는 완비 모듈러 격자를 이룬다.^{[8]:16, Exercise 3.6} 이 격자에서 만남 ${\displaystyle \wedge }$은 두 양쪽 아이디얼의 교집합이며, 이음 ${\displaystyle \vee }$는 두 양쪽 아이디얼의 합 아이디얼이다.

${\displaystyle {\mathfrak {a}}\wedge {\mathfrak {b}}={\mathfrak {a}}\cap {\mathfrak {b}}}$

${\displaystyle {\mathfrak {a}}\vee {\mathfrak {b}}={\mathfrak {a}}+{\mathfrak {b}}}$

아이디얼의 격자가 분배 격자인 환은 산술환(영어: arithmetical ring)이라고 한다.

마찬가지로, ${\displaystyle R}$의 모든 왼쪽 아이디얼들의 부분 순서 집합이나, 오른쪽 아이디얼들의 부분 순서 집합 역시 완비 모듈러 격자를 이룬다. (이는 모든 가군의 부분 가군 격자가 완비 모듈러 격자라는 정리의 특수한 경우이다.)

또한, ${\displaystyle R}$의 유한 생성 양쪽 아이디얼들의 부분 순서 집합은 모듈러 이음 반격자(영어: modular join-semilattice)를 이룬다.^{[9]:189, Exercise 5.44}

환 ${\displaystyle R}$의 부분환들의 부분 순서 집합 ${\displaystyle (\operatorname {Sub} (R),\subseteq )}$ 역시 완비 격자를 이루며, 추가로 대수적 격자를 이룬다.

종류

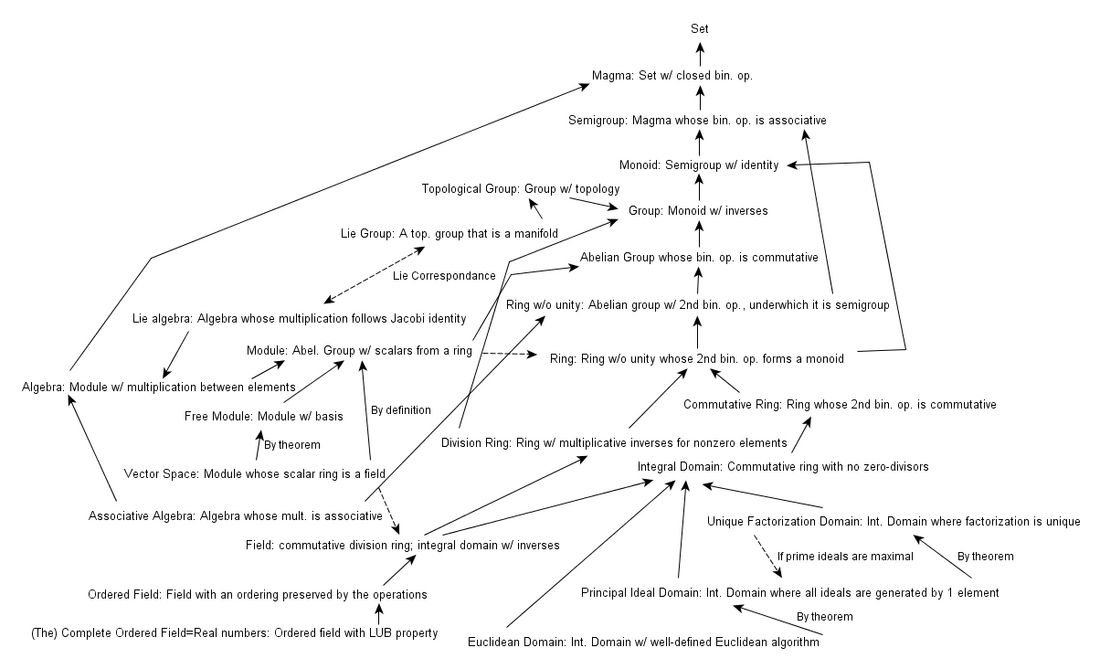
다양한 종류의 특별한 환들은 특별한 이름을 갖는다. 이들 가운데 대표적인 것들 및 이들 사이의 함의 관계는 다음과 같다.^[10]:153

체	⇒	정역
⇓		⇓	⇘
나눗셈환	⇒	영역	⇒	축소환
⇓		⇓		⇓
左·右 원시환	⇒	소환	⇒	반소환

위 개념들과 독립적으로, 뇌터 환은 "지나치게 크지 않은" 환이다. 아르틴 환은 "매우 작은 (0차원)" 환이다. 모든 아르틴 환은 뇌터 환이나, 그 역은 성립하지 않는다.

가환환

 이 부분의 본문은 가환환입니다.

곱셈에 대해 교환 법칙이 성립하는 환을 가환환이라고 한다. 가환환의 경우 다양한 특수한 개념들이 존재하는데, 그 포함 관계는 다음과 같다.

가환환 ⊋ 정역 ⊋ 정수적으로 닫힌 정역 ⊋ 크룰 정역 ⊋ 유일 인수 분해 정역 ∪ 데데킨트 정역 ⊋ 유일 인수 분해 정역 ∩ 데데킨트 정역 = 주 아이디얼 정역 ⊋ 유클리드 정역 ⊋ 체

특히, 모든 체는 가환환이다.

만약 덧셈에 대한 항등원 0을 제외한 모든 환의 원소가 곱셈에 대한 역원을 가지고 있다면 이를 나눗셈환이라고 부른다. 가환환인 나눗셈환은 체와 같다.

분류

모든 환들을 분류하는 것은 현재 수학으로서는 불가능하다. 다만, 일반적인 환에 대하여 다음과 같은 4단계의 대략적인 구조론이 존재한다.^{[10]:196, (12.8)}

1. 임의의 환 ${\displaystyle R}$는 그 제이컵슨 근기 ${\displaystyle \operatorname {J} (R)}$ 및 몫환 ${\displaystyle R/\operatorname {J} (R)}$로 분해되며, 제이컵슨 근기에 대한 몫환은 항상 반원시환이다.
2. 모든 반원시환 ${\displaystyle R}$는 왼쪽 원시환들의 직접곱 ${\displaystyle \textstyle \prod _{i}R_{i}}$의 부분환 ${\displaystyle \textstyle R\subseteq \prod _{i}R_{i}}$으로 나타내어지며, 이 경우 사영 준동형 ${\displaystyle R\to R_{i}}$는 전사 함수이다.
3. 모든 왼쪽 원시환 ${\displaystyle R}$는 나눗셈환 ${\displaystyle D}$ 위의 자유 가군 ${\displaystyle V}$의 선형 변환환 ${\displaystyle \operatorname {End} _{D}V}$의 (적절한 위상에서의) 조밀 집합인 부분환 ${\displaystyle R\subseteq \operatorname {End} _{D}V}$이다. (제이컵슨 조밀성 정리)
4. 모든 나눗셈환 ${\displaystyle D}$에 대하여, 그 중심 ${\displaystyle Z(D)}$는 체를 이루며, ${\displaystyle D}$는 체 ${\displaystyle Z(D)}$ 위의 단위 결합 대수를 이룬다.

특별한 종류의 환들의 경우, (거의) 완전한 분류가 존재한다. 예를 들어, 많은 종류의 유한환은 완전히 분류되었고, 마찬가지로 아르틴 단순환 및 반단순환 역시 완전히 분류되었다 (아르틴-웨더번 정리).

예

• 정수의 집합 ${\displaystyle \mathbb {Z} }$에 (표준적인) 덧셈과 곱셈을 부여하면, 가환환을 이룬다. 이는 한원소 집합 위의 자유환이다.
• 모든 체는 환을 이룬다. 예를 들어, 유리수의 집합 ${\displaystyle \mathbb {Q} }$, 실수의 집합 ${\displaystyle \mathbb {R} }$, 복소수의 집합 ${\displaystyle \mathbb {C} }$는 체이며 따라서 환을 이룬다.
• ${\displaystyle n}$이 양의 정수일 때, 몫환 ${\displaystyle \mathbb {Z} /n\mathbb {Z} }$는 환을 이룬다. 이 몫환은 합동 산술의 기초를 이룬다.
• 한원소 집합 ${\displaystyle \{0\}}$에, 연산 ${\displaystyle 0+0=0\cdot 0=0}$을 부여하면 환을 이룬다. 이를 자명환이라고 한다.
• 위상 공간 ${\displaystyle X}$ 위에 정의된 실수 연속 함수의 집합 ${\displaystyle {\mathcal {C}}(X,\mathbb {R} )}$은 가환환을 이룬다. 이때, 연산은 각 함수값의 덧셈과 곱셈이다. 즉, 함수 ${\displaystyle f(x)}$ 와 ${\displaystyle g(x)}$의 합과 곱은 다음과 같은 값을 갖는 함수로 정의한다.

  ${\displaystyle f+g\colon x\mapsto f(x)+g(x)}$

  ${\displaystyle fg\colon x\mapsto f(x)g(x)}$

• 어떤 환 ${\displaystyle R}$이 주어졌을 때, 다항식환 ${\displaystyle R[x_{1},x_{2},\cdots ,x_{n}]}$은 환을 이룬다. 만약 ${\displaystyle R}$가 가환환이라면 다항식환 역시 가환환이다.
• 환 ${\displaystyle R}$ 및 자연수 ${\displaystyle n}$이 주어졌을 때, ${\displaystyle R}$의 원소들의 ${\displaystyle n\times n}$ 정사각행렬의 집합 ${\displaystyle \operatorname {Mat} (R;n)}$은 행렬의 덧셈과 곱셈에 대하여 환을 이루며, 이를 행렬환이라고 한다. 일반적으로 이는 가환환이 아니다.
• 불 대수 ${\displaystyle (B,\land ,\lor )}$ (예를 들어, 어떤 집합의 멱집합)는 다음과 같이 가환환의 구조를 줄 수 있다.

  ${\displaystyle a+b=(a\lor b)\land \lnot (a\land b)}$

  ${\displaystyle ab=a\land b}$

역사

환의 연구는 다항식환 및 수체의 대수적 정수의 이론으로부터 출발했다. 환의 개념은 리하르트 데데킨트가 도입했으며, 1897년에 다비트 힐베르트가 수체의 대수적 정수환을 다루는 동안 처음으로 "수환"(독일어: Zahlring 찰링^[*] = 독일어: Zahl 찰^[*](數) + 독일어: Ring 링^[*](環))이라는 용어를 사용하였다.^[11]

아브라함 프렝켈은 1914년에^[12] 처음으로 환을 엄밀히 정의했으며, 에미 뇌터는 1921년의 논문^[13]에서 가환환의 이론을 공리적으로 전개하였다.

각주

1. Lang, Serge (2002). 《Algebra》. Graduate Texts in Mathematics (영어) 211 3판. Springer. doi:10.1007/978-1-4613-0041-0. ISBN 978-1-4612-6551-1. ISSN 0072-5285. MR 1878556. Zbl 0984.00001.
2. Cohn, Paul Moritz (1982). 《Algebra. Volume 1》 (영어) 2판. John Wiley & Sons. Zbl 0481.00001. CS1 관리 - 추가 문구 (링크)
3. Dummit, David S.; Richard M. Foote (2004). 《Abstract algebra》 (영어) 3판. Wiley. ISBN 978-0-471-43334-7. MR 2286236. Zbl 1037.00003. 더 이상 지원되지 않는 변수를 사용함 (도움말)
4. Grillet, Pierre Antoine (2007). 《Abstract algebra》. Graduate Texts in Mathematics (영어) 242. Springer. doi:10.1007/978-0-387-71568-1. ISBN 978-0-387-71567-4. ISSN 0072-5285.
5. “Some characterizations of ring epimorphisms” (PDF) (영어).
6. “Classification of finite rings of order ${\displaystyle p^{2}}$” (PDF). 《Mathematics Magazine》 (영어) 66 (4): 248–252. 1993년 10월. doi:10.2307/2690742. ISSN 0025-570X. JSTOR 2690742. 2015년 4월 11일에 원본 문서 (PDF)에서 보존된 문서. 2015년 4월 21일에 확인함. |제목=에 지움 문자가 있음(위치 41) (도움말)
7. Fuchs, L. 《Infinite Abelian groups, volume 2》 (영어).
8. Burris, Stanley N.; Hanamantagouda P. Sankappanavar (1981). 《A course in universal algebra》. Graduate Texts in Mathematics (영어) 78. Springer. ISBN 978-1-4613-8132-7. ISSN 0072-5285. MR 0648287. Zbl 0478.08001. 더 이상 지원되지 않는 변수를 사용함 (도움말)
9. Grätzer, George (2011). 《Lattice theory: foundation》 (영어). Springer. doi:10.1007/978-3-0348-0018-1. ISBN 978-3-0348-0017-4.
10. Lam, Tsit-Yuen (2001). 《A first course in noncommutative rings》. Graduate Texts in Mathematics (영어) 131 2판. Springer. doi:10.1007/978-1-4419-8616-0. ISBN 978-0-387-95183-6. ISSN 0072-5285.
11. Hilbert, David (1897). “Die Theorie der algebraischen Zahlkörper”. 《Jahresbericht der Deutschen Mathematiker Vereinigung》 (독일어) 4: 175–546. JFM 28.0157.05.
12. Fraenkel, Adolf (1914). “Über die Teiler der Null und die Zerlegung von Ringen”. 《Journal für die reine und angewandte Mathematik》 (독일어) 145: 139–176. doi:10.1515/crll.1915.145.139. ISSN 0075-4102. JFM 45.0324.02.
13. Noether, Emmy (1921). “Idealtheorie in Ringbereichen”. 《Mathematische Annalen》 (독일어) 83 (1–2): 24–66. doi:10.1007/BF01464225. ISSN 0025-5831. JFM 48.0121.03. 2015년 7월 12일에 원본 문서에서 보존된 문서. 2015년 4월 16일에 확인함.

같이 보기

• 체 (수학)
• 군 (수학)
• 유사환

외부 링크

• “Ring”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
• “Associative rings and algebras”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
• Weisstein, Eric Wolfgang. “Ring”. 《Wolfram MathWorld》 (영어). Wolfram Research.
• Weisstein, Eric Wolfgang. “Unit ring”. 《Wolfram MathWorld》 (영어). Wolfram Research.
• “Ring”. 《nLab》 (영어).
• “Category of rings”. 《nLab》 (영어).