벡터 공간

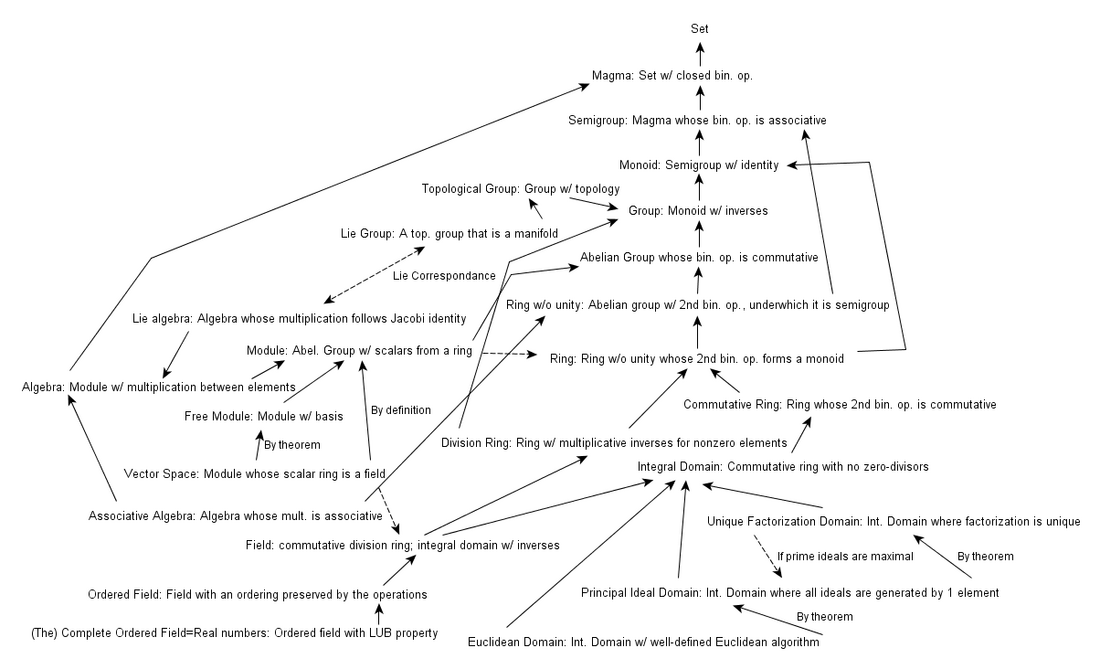
선형대수학에서 벡터 공간(vector空間, 영어: vector space, 문화어: 벡토르공간, 선형공간^[1][2]) 또는 선형 공간(線型空間, 영어: linear space)은 원소를 서로 더하거나 주어진 배수로 늘이거나 줄일 수 있는 공간이다. 체에 대한, 가군의 특수한 경우다. 벡터 공간의 원소를 벡터(영어: vector, 문화어: 벡토르^[3])라고 하며, 이는 직관적으로 방향 및 길이의 비가 정의된 대상을 나타낸다. 그러나 노름이 주어지지 않은 일반적인 벡터 공간에서는 벡터의 길이 자체는 정의되지 않는다.

다른 뜻에 대해서는 벡터 문서를 참고하십시오.

정의

체 ${\displaystyle K}$ 위의 벡터 공간 ${\displaystyle (V,+,\cdot )}$은 ${\displaystyle K}$에 대한 가군이다. 즉, 다음과 같은 튜플이다.

• ${\displaystyle V}$는 집합이다. 이 집합의 원소를 벡터라고 한다.
• ${\displaystyle +\colon V\times V\to V}$는 함수이다. 이 연산을 벡터 덧셈이라고 한다.
• ${\displaystyle \cdot \colon K\times V\to V}$는 함수이다. 이 연산을 스칼라 곱셈이라고 한다.

이 데이터는 다음과 같은 공리들을 만족시켜야 한다.

• ${\displaystyle (V,+)}$는 아벨 군을 이룬다. 즉, 다음 성질들이 성립한다.
  • (벡터 덧셈의 결합 법칙) 임의의 ${\displaystyle u,v,w\in V}$에 대하여, ${\displaystyle (u+v)+w=u+(v+w)}$
  • (벡터 덧셈의 교환 법칙) 임의의 ${\displaystyle u,v\in V}$에 대하여, ${\displaystyle u+v=v+u}$
  • (벡터 덧셈의 항등원) 임의의 ${\displaystyle u\in V}$에 대하여 ${\displaystyle u+0=u}$인 원소 ${\displaystyle 0\in V}$가 존재한다.
  • (역원의 존재) 임의의 ${\displaystyle u\in V}$에 대하여, ${\displaystyle -u+u=0}$인 원소 ${\displaystyle -u\in V}$가 존재한다.
• ${\displaystyle (V,+,\cdot )}$는 ${\displaystyle K}$의 가군을 이룬다. 즉, 다음 성질들이 성립한다.
  • 임의의 ${\displaystyle a,b\in K}$ 및 ${\displaystyle v\in V}$에 대하여, ${\displaystyle a\cdot (b\cdot v)=(ab)\cdot v}$
  • 임의의 ${\displaystyle v\in V}$에 대하여, ${\displaystyle 1\cdot v=v}$. 여기서 ${\displaystyle 1\in K}$는 ${\displaystyle K}$의 곱셈 항등원이다.
  • (분배 법칙) 임의의 ${\displaystyle a,b\in K}$ 및 ${\displaystyle u,v\in V}$에 대하여, ${\displaystyle (a+b)\cdot (u+v)=a\cdot u+b\cdot u+a\cdot v+b\cdot v}$

실수체 ${\displaystyle \mathbb {R} }$에 대한 벡터 공간을 실수 벡터 공간(實數vector空間, 영어: real vector space)이라고 하며, 복소수체 ${\displaystyle \mathbb {C} }$에 대한 벡터 공간을 복소수 벡터 공간(複素數vector空間, 영어: complex vector space)이라고 한다.

부분 공간과 기저

체 ${\displaystyle K}$ 위의 벡터 공간 ${\displaystyle V}$의 부분 집합 ${\displaystyle W\subseteq V}$가 다음 조건을 만족시키면, ${\displaystyle W}$가 ${\displaystyle V}$의 부분 벡터 공간(部分vector空間, 영어: vector subspace)이라고 한다.

• ${\displaystyle 0_{V}\in W}$
• 임의의 ${\displaystyle u,v\in W}$에 대하여, ${\displaystyle u+v\in W}$
• 임의의 ${\displaystyle a\in K}$ 및 ${\displaystyle u\in W}$에 대하여, ${\displaystyle a\cdot u\in W}$

즉, 부분 벡터 공간은 ${\displaystyle V}$의 연산들을 제한시켜 새로운 더 작은 벡터 공간을 이룰 수 있는 부분 집합이다.

벡터 공간 ${\displaystyle V}$의 부분 집합 ${\displaystyle S}$에 대하여, ${\displaystyle S}$의 생성(영어: span) ${\displaystyle \operatorname {Span} S}$는 ${\displaystyle S}$를 포함하는 모든 부분 공간들의 교집합이다. 만약 ${\displaystyle S}$에서, ${\displaystyle s\in \operatorname {Span} (S\setminus \{s\})}$인 원소 ${\displaystyle s\in S}$가 존재하지 않는다면, ${\displaystyle S}$가 선형 독립 집합이라고 한다. 생성이 벡터 공간 전체인 선형 독립 집합을 기저라고 한다.

선택 공리를 가정하면, 모든 벡터 공간은 하나 이상의 기저를 가지며, 모든 기저들은 항상 같은 크기를 갖는다. 벡터 공간 ${\displaystyle V}$의 기저의 크기를 벡터 공간의 차원(次元, 영어: dimension) ${\displaystyle \dim V\in \operatorname {Card} }$이라고 한다.

선형 변환

 이 부분의 본문은 선형 변환입니다.

두 벡터 공간 사이의 선형 변환은 벡터 덧셈과 스칼라 곱셈을 보존하는 사상이다. 만약 두 벡터 공간 사이에 가역 선형 변환이 존재한다면, 그 두 벡터 공간이 서로 동형이라고 한다. 주어진 두 벡터 공간 사이의 선형 변환의 집합은 점별 벡터 덧셈과 점별 스칼라 곱셈에 의하여 벡터 공간을 이룬다. 두 유한 차원 벡터 공간 사이의 선형 변환은 주어진 기저에 대한 행렬로 나타낼 수 있다.

분류

선택 공리를 가정하자. 체 ${\displaystyle K}$에 대한 벡터 공간 ${\displaystyle V}$에 대하여 다음이 성립한다.

${\displaystyle V\cong K^{\oplus \dim V}}$

즉, 주어진 체에 대한 벡터 공간은 그 차원에 따라서 완전히 분류된다. 이는 선택 공리를 필요로 하며, 선택 공리가 없으면 모든 벡터 공간이 차원을 갖는다는 것을 보일 수 없다. 여기서 ${\displaystyle K^{\oplus \dim V}}$는 ${\displaystyle K}$의 ${\displaystyle \dim V}$개의 직합이며, ${\displaystyle \dim V\geq \aleph _{0}}$인 경우 이는 곱집합과 다르다.

연산

같은 체 ${\displaystyle K}$ 위의 벡터 공간들이 주어졌을 때, 다음과 같은 연산들을 정의할 수 있다.

선분과 벡터 공간

몫공간

체 ${\displaystyle K}$ 위의 벡터 공간 ${\displaystyle V}$와 그 임의의 부분 공간 ${\displaystyle W}$가 주어졌다고 하자. 그렇다면 ${\displaystyle V}$ 위에 다음과 같은 동치 관계를 정의할 수 있다.

${\displaystyle v\sim w\iff v-w\in W}$

이 동치 관계에 대한 동치류는 다음과 같다.

${\displaystyle [v]_{\sim }=v+W=\{v+w\colon w\in W\}\qquad (v\in V)}$

몫공간(몫空間, 영어: quotient space) ${\displaystyle V/W}$는 집합으로서 이 동치 관계에 대한 몫집합(=동치류들의 집합)이다.

${\displaystyle V/W=\{v+W\colon v\in V\}}$

그 위의 벡터 공간 연산은 다음과 같다.

${\displaystyle (v+W)+(w+W)=(v+w)+W}$

${\displaystyle a\cdot (v+W)=a\cdot v+W}$

이 정의는 동치류의 대표원을 선택하는 방식과 무관하다. 또한, 이들 연산은 집합으로서의 연산과 일치하지 않는다.

직접곱

 이 부분의 본문은 직접곱입니다.

${\displaystyle K}$ 위의 벡터 공간들의 집합 ${\displaystyle \{V_{i}\}_{i\in I}}$이 주어졌을 때, 이들의 직접곱

${\displaystyle \prod _{i\in I}V_{i}}$

은 집합으로서 ${\displaystyle V_{i}}$들의 곱집합이다. 이 위에는 자연스러운 ${\displaystyle K}$-벡터 공간의 구조가 존재한다. 즉,

${\displaystyle (a_{i})_{i\in I}+(b_{i})_{i\in I}=(a_{i}+b_{i})_{i\in I}}$

${\displaystyle c\cdot (a_{i})_{i\in I}=(c\cdot a_{i})_{i\in I}}$

이는 벡터 공간의 범주에서의 곱이며, 대수 구조로서의 직접곱이다. 즉, 자연스러운 사영 사상

${\displaystyle \pi _{i}\colon \prod _{i\in I}V_{i}\to V_{i}}$

이 존재하며, 이는 선형 변환을 이룬다.

직합

 이 부분의 본문은 직합입니다.

${\displaystyle K}$ 위의 벡터 공간들의 집합 ${\displaystyle \{V_{i}\}_{i\in I}}$이 주어졌을 때, 이들의 직합은 다음과 같다.

${\displaystyle \bigoplus _{i\in I}V_{i}=\left\{a\in \prod _{i\in I}V_{i}\colon |\{i\in I\colon a_{i}\neq 0\}|<\aleph _{0}\right\}\subseteq \prod _{i\in I}V_{i}}$

즉, 직접곱에서, 오직 유한 개의 성분만 0이 아닌 원소들로 구성된 부분 집합이다. 이는 벡터 공간의 범주에서의 쌍대곱이며, 가군의 직합의 특수한 경우이다. 즉, 자연스러운 포함 사상

${\displaystyle \iota _{i}\colon V_{i}\hookrightarrow \bigoplus _{i\in I}V_{i}}$

가 존재하며, 따라서 각 ${\displaystyle V_{i}}$는 ${\displaystyle \bigoplus _{i\in I}V_{i}}$의 부분 공간을 이룬다.

유한 직합은 직접곱과 같으나, 무한 직합은 일반적으로 직접곱의 부분 공간이다. 만약 ${\displaystyle S_{i}\subset V_{i}}$가 ${\displaystyle V_{i}}$의 기저라면,

${\displaystyle \bigcup _{i\in I}\iota _{i}(S_{i})\subset \bigoplus _{i\in I}V_{i}}$

는 ${\displaystyle \bigoplus _{i\in I}V_{i}}$의 기저를 이룬다. 따라서,

${\displaystyle \dim \bigoplus _{i\in I}V_{i}=\sum _{i\in I}\dim V_{i}}$

이다. 여기서 우변은 기수의 합이다.

텐서곱

${\displaystyle K}$ 위의 벡터 공간들의 집합 ${\displaystyle \{V_{i}\}_{i\in I}}$이 주어졌을 때, 이들의 텐서곱

${\displaystyle \bigotimes _{i\in I}V_{i}=\operatorname {Free} \left(\prod _{i\in I}V_{i}\right)/\sim }$

이 존재한다. 이는 자연스러운 다중 선형 사상

${\displaystyle \phi \colon \prod _{i\in I}V_{i}\to \bigotimes _{i\in I}V_{i}}$

을 가지며, 또한 임의의 다른 다중 선형 사상

${\displaystyle \chi =\prod _{i\in I}V_{i}\to W}$

이 주어졌을 때, 유일한 선형 사상

${\displaystyle {\tilde {\chi }}\colon \bigotimes _{i\in I}V_{i}\to W}$

${\displaystyle {\tilde {\chi }}\circ \phi =\chi }$

가 존재한다. 텐서곱은 이 보편 성질로부터 유일하게 정의되며, 또 항상 존재한다.^[4] 그러나 무한 개의 벡터 공간들의 텐서곱은 직접 정의하기 힘들다.

임의의 두 벡터 공간 ${\displaystyle V}$, ${\displaystyle W}$에 대하여, 다음이 성립한다.

${\displaystyle \dim(V\otimes W)=\dim V\cdot \dim W}$

여기서 ${\displaystyle \cdot }$은 기수의 곱셈이다.

성질

체 ${\displaystyle K}$ 위의 벡터 공간 ${\displaystyle K}$는 다음 성질들을 만족시킨다.

• 사영 가군이다.
• 평탄 가군이다.
• 자유 가군이다.

즉, 체 위에서는 모든 가군이 자유 가군이 된다.

집합론적 성질

체 ${\displaystyle K}$ 위의 벡터 공간 ${\displaystyle V}$의 집합의 크기는 다음과 같다.

${\displaystyle |V|={\begin{cases}|K|^{\dim _{K}V}&\kappa <\aleph _{0}\\\max\{|K|,\dim _{K}V\}&\kappa \geq \aleph _{0}\end{cases}}}$

범주론적 성질

체 ${\displaystyle K}$에 대한 벡터 공간들과 이들 사이의 선형 변환들은 범주를 이루며, ${\displaystyle \operatorname {Vect} _{K}}$라고 쓴다. 이는 아벨 범주의 대표적인 예이다. ${\displaystyle \operatorname {Vect} _{K}}$에서의 대표적 범주론적 연산들은 다음과 같다.

• 완비 범주이며, 쌍대 완비 범주이다.
  • 곱은 (아벨 군으로서의) 직접곱이며, 쌍대곱은 (아벨 군으로서의) 직합이다.
  • (유한) 곱과 쌍대곱이 일치한다.
  • 영 대상은 0차원 벡터 공간 ${\displaystyle \{0\}}$이다.
• 직합 말고도, 텐서곱 ${\displaystyle V\otimes W}$을 가지며, 이에 따라 ${\displaystyle \operatorname {Vect} _{K}}$는 대칭 모노이드 범주를 이룬다. 텐서곱의 항등원은 1차원 벡터 공간 ${\displaystyle K}$이다.
• 집합으로의 망각 함자 ${\displaystyle F\colon \operatorname {Vect} _{K}\to \operatorname {Set} }$, ${\displaystyle (V,+,\cdot )\mapsto V}$가 존재하며, 이에 따라서 구체적 범주를 이룬다. 망각 함자는 왼쪽 수반 함자 ${\displaystyle \operatorname {Span} \dashv F}$를 갖는데, ${\displaystyle \operatorname {Span} }$은 집합 ${\displaystyle S}$를 ${\displaystyle |S|}$차원 벡터 공간으로 대응시킨다.

모형 이론적 성질

모형 이론의 관점에서, 체 ${\displaystyle K}$에 대한 벡터 공간의 개념은 대수 구조로 나타낼 수 있다. 이 경우, 벡터 공간의 언어는 다음과 같은 연산을 갖는다.

• 0항 연산 ${\displaystyle 0}$ (영벡터)
• 각 ${\displaystyle a\in K}$에 대하여, 1항 연산 ${\displaystyle a\cdot }$
• 2항 연산 ${\displaystyle +}$

즉, 만약 ${\displaystyle K}$가 무한 집합일 경우, 벡터 공간의 언어는 무한 개의 연산을 갖는다. 벡터 공간을 정의하는 공리들은 모두 항등식으로 적을 수 있으므로, 벡터 공간들의 모임은 대수 구조 다양체를 이룬다. 벡터 공간의 준동형은 선형 변환이며, 벡터 공간의 부분 대수는 부분 벡터 공간이다. 합동 관계는 부분 벡터 공간과 일대일 대응하며, 주어진 합동 관계에 대응하는 부분 공간은 0과 합동인 벡터들의 집합이다. 특이하게도, 모든 벡터 공간은 자유 대수이다.

예

• 유클리드 공간 ${\displaystyle \mathbb {R} ^{n}}$은 ${\displaystyle n}$차원 실수 벡터 공간이다.
• 체 ${\displaystyle K}$ 위의 ${\displaystyle m\times n}$ 행렬의 집합은 ${\displaystyle mn}$차원 ${\displaystyle K}$-벡터 공간을 이룬다.
• 임의의 위상 공간 ${\displaystyle X}$ 위의 모든 연속 실함수의 집합 ${\displaystyle {\mathcal {C}}(X,\mathbb {R} )}$는 실수 벡터 공간을 이룬다.
• 체 ${\displaystyle K}$ 위의 벡터 공간 V 와 어떤 집합 ${\displaystyle X}$가 주어졌을 때, ${\displaystyle X}$에서 ${\displaystyle V}$로의 함수 ${\displaystyle f\colon X\to V}$들의 집합은 ${\displaystyle F}$ 위의 벡터 공간을 이룬다. 이는 ${\displaystyle V}$의 ${\displaystyle |X|}$개 직접곱 ${\displaystyle V^{\times |X|}}$과 동형이다.
• 체 ${\displaystyle K}$에 대하여, 다항식환 ${\displaystyle K[x]}$ 및 형식적 거듭제곱 급수환 ${\displaystyle F[[x]]}$는 ${\displaystyle K}$ 위의 벡터 공간이다.
• 임의의 체의 확대 ${\displaystyle L/K}$의 경우, ${\displaystyle L}$은 ${\displaystyle K}$ 위의 벡터 공간을 이루며, 벡터 공간으로서의 차원은 체의 확대의 차수이다.
  • 유한체 ${\displaystyle \mathbb {F} _{p^{n}}}$은 ${\displaystyle \mathbb {F} _{p}}$ 위의 ${\displaystyle n}$차원 벡터 공간이다.
  • ${\displaystyle \mathbb {C} }$는 ${\displaystyle \mathbb {R} }$ 위의 2차원 벡터 공간이다.
  • ${\displaystyle \mathbb {R} }$는 ${\displaystyle \mathbb {Q} }$ 위의 ${\displaystyle 2^{\aleph _{0}}}$차원 벡터 공간이다.
  • 모든 대수적 수체는 ${\displaystyle \mathbb {Q} }$ 위의 벡터 공간이다.

관련 개념

벡터 공간에 성질을 추가하여 만든 구조로는 거리의 개념을 준 노름 공간 · 바나흐 공간, 각의 개념을 준 내적 공간 · 힐베르트 공간, 위상적 성질을 가진 위상 벡터 공간 · 국소 볼록 공간 · 프레셰 공간, 벡터 곱을 준 체 위의 대수 등이 있다.

벡터 공간은 임의의 환 위의 가군의 개념의 특수한 경우이다. 그러나 일반적인 환 위의 일반적인 가군은 벡터 공간과 매우 다른 성질을 보인다. 벡터 공간과 비슷한 성질을 보이는 가군을 자유 가군이라고 한다.

같이 보기

• 사원수
• 행렬식

각주

1. “벡토르공간”. 북한과학기술네트워크. 2021년 6월 16일에 원본 문서에서 보존된 문서. 2015년 9월 5일에 확인함.
2. “선형공간 (linear space)”. 북한과학기술네트워크. 2021년 6월 16일에 원본 문서에서 보존된 문서. 2015년 9월 5일에 확인함.
3. “벡토르 (vector)”. 북한과학기술네트워크. 2021년 6월 16일에 원본 문서에서 보존된 문서. 2015년 9월 5일에 확인함.
4. Ng, Chi-Keung (2013). “On genuine infinite algebraic tensor products”. 《Revista Matemática Iberoamericana》 (영어) 29 (1): 329–356. arXiv:1112.3128. doi:10.4171/RMI/722.

참고 문헌

• 김경호 (2013년 9월 2일). 《선형대수학의 이해》 개정판. 서울: 교우사. ISBN 978-89-8172-012-4. 2014년 4월 14일에 원본 문서에서 보존된 문서. 2015년 1월 17일에 확인함.
• 조용욱 (2000). 《선형대수학원론》. 서울: 교우사.

외부 링크

• “Vector space”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
• Weisstein, Eric Wolfgang. “Vector space”. 《Wolfram MathWorld》 (영어). Wolfram Research.
• “Vector space”. 《nLab》 (영어).
• “Finite-dimensional vector space”. 《nLab》 (영어).
• “Vect”. 《nLab》 (영어).
• “벡터 공간”. 《오메가》. 2016년 3월 5일에 원본 문서에서 보존된 문서. 2015년 2월 28일에 확인함.
• “임의의 벡터 공간은 기저를 갖는다”. 《오메가》. 2016년 3월 6일에 원본 문서에서 보존된 문서. 2015년 2월 28일에 확인함.
• “Infinite Tensor Products” (영어). Math Overflow.