Solido di Johnson
Da Wikipedia, l'enciclopedia libera
In geometria un solido di Johnson è un poliedro convesso le cui facce sono tutte costituite da poligoni regolari, ma che non è né un solido platonico, né un solido archimedeo, né un prisma, né un antiprisma. Le diverse facce possono essere poligoni con numeri diversi di lati. Il più semplice esempio di solido di Johnson è la piramide a base quadrata; essa ha una faccia quadrata e quattro facce triangolari.

I solidi di Johnson sono 92, e vengono generalmente indicati con una sigla che va da fino a .
Storia
Nel 1966, Norman Johnson ha pubblicato una lista di poliedri che include tutti i 92 solidi e ha dato loro i nomi e i numeri da allora entrati nell'uso. Egli non ha dimostrato che di tali solidi ce ne fossero solo 92, ma ha avanzato questa congettura. La dimostrazione che la lista trovata da Johnson fosse completa è stata fornita da Victor Zalgaller nel 1969.
Proprietà
Valenze ai vertici
Come in ogni solido strettamente convesso, in ogni vertice incidono almeno tre facce e l'ampiezza totale dei loro angoli deve essere inferiore a 360°. Dato che un poligono regolare possiede angoli di almeno 60°, accade che in ogni vertice incidono al più cinque facce. La piramide pentagonale (J2) costituisce un esempio di solido con un vertice di valenza 5.
Tra i solidi di Johnson la girobicupola quadrata elongata (J37) è l'unica che risulta essere localmente regolare sui vertici: in ogni vertice incidono quattro facce e la composizione di queste quaterne è sempre la stessa: tre quadrati e un triangolo.
Facce
Gli unici poligoni che sono facce di qualche poliedro di Johnson hanno numero di lati pari a 3, 4, 5, 6, 8 o 10. Questo dato è il risultato della classificazione: non sembrano esserci modi più diretti per mostrare che solo questi valori sono ammessi.
Nomi
Riepilogo
Prospettiva
A prima vista i nomi dei poliedri di Johnson sembrano complicate bizzarrie; in realtà sono stati scelti in modo da risultare il più possibile descrittivi. Per padroneggiare i significati dei nomi bisogna osservare che gran parte dei solidi di Johnson si possono costruire con elaborazioni relativamente semplici a partire da poliedri piuttosto semplici: le prime piramidi, le cupole, le rotunde, i solidi platonici, i solidi archimedei, i prismi e gli antiprismi. Vediamo quindi il significato degli elementi lessicali utilizzati nei nomi.
- Il prefisso bi- significa che vengono unite per le basi due copie del solido richiamato successivamente. Le cupole e le rotunde si possono unire facendo incontrare o facce simili (si usa il prefisso (orto-) o facce dissimili (si usa il prefisso giro-). Secondo questa nomenclatura, un ottaedro viene chiamato bipiramide quadrata, un cubottaedro viene detto girobicupola e un icosidodecaedro viene chiamato girobirotonda pentagonale.
- L'aggettivo elongato significa che è stato incollato un prisma alla base del solido richiamato o tra le basi dei solidi richiamati. Un rombicubottaedro diventa anche una ortobicupola quadrata elongata.
- L'aggettivo giroelongato viene usato quando è stato incollato un antiprisma alla base del solido in questione o tra le basi di due solidi in questione. Un icosaedro sarebbe una bipiramide pentagonale giroelongata.
- Aumentato significa che una piramide o una cupola è stata aggiunta a una faccia del solido in questione.
- Diminuito viene usato quando dal solido richiamato è stata rimossa una piramide o una cupola.
- Girato esprime il fatto che una cupola posta sul solido in questione è stata ruotata in modo che vengano a coincidere coppie di spigoli prima distinti, come per la differenza tra ortobicupole e girobicupole.
Nomi e numeri di Johnson
Riepilogo
Prospettiva
I nomi e i numeri di Johnson per i solidi in esame sono i seguenti.
Piramidi, cupole e rotonda | |||||||||||||
| Jn | Nome | Immagine | Tipo | V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | Simmetria |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Piramide quadrata | Piramide | 5 | 8 | 5 | 4 | 1 | 0 | 0 | 0 | 0 | C4v | |
| 2 | Piramide pentagonale | Piramide | 6 | 10 | 6 | 5 | 0 | 1 | 0 | 0 | 0 | C5v | |
| 3 | Cupola triangolare |  |
Cupola | 9 | 15 | 8 | 4 | 3 | 0 | 1 | 0 | 0 | C3v |
| 4 | Cupola quadrata |  |
Cupola | 12 | 20 | 10 | 4 | 5 | 0 | 0 | 1 | 0 | C4v |
| 5 | Cupola pentagonale |  |
Cupola | 15 | 25 | 12 | 5 | 5 | 1 | 0 | 0 | 1 | C5v |
| 6 | Rotonda pentagonale |  |
Rotonda | 20 | 35 | 17 | 10 | 0 | 6 | 0 | 0 | 1 | C5v |
Piramidi modificate | |||||||||||||
| Jn | Nome | Immagine | Tipo | V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | Simmetria |
| 7 | Piramide triangolare elongata |  |
Piramide elongata | 7 | 12 | 7 | 4 | 3 | 0 | 0 | 0 | 0 | C3v |
| 8 | Piramide quadrata elongata |  |
Piramide elongata | 9 | 16 | 9 | 4 | 5 | 0 | 0 | 0 | 0 | C4v |
| 9 | Piramide pentagonale elongata | 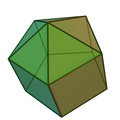 |
Piramide elongata | 11 | 20 | 11 | 5 | 5 | 1 | 0 | 0 | 0 | C5v |
| 10 | Piramide quadrata giroelongata |  |
Piramide giroelongata | 9 | 20 | 13 | 12 | 1 | 0 | 0 | 0 | 0 | C4v |
| 11 | Piramide pentagonale giroelongata |  |
Piramide giroelongata | 11 | 25 | 16 | 15 | 0 | 1 | 0 | 0 | 0 | C5v |
| 12 | Dipiramide triangolare |  |
Dipiramide | 5 | 9 | 6 | 6 | 0 | 0 | 0 | 0 | 0 | D3h |
| 13 | Dipiramide pentagonale |  |
Dipiramide | 7 | 15 | 10 | 10 | 0 | 0 | 0 | 0 | 0 | D5h |
| 14 | Bipiramide triangolare elongata |  |
Bipiramide elongata | 8 | 15 | 9 | 6 | 3 | 0 | 0 | 0 | 0 | D3h |
| 15 | Bipiramide quadrata elongata |  |
Bipiramide elongata | 10 | 20 | 12 | 8 | 4 | 0 | 0 | 0 | 0 | D4h |
| 16 | Bipiramide pentagonale elongata |  |
Bipiramide elongata | 12 | 25 | 15 | 10 | 5 | 0 | 0 | 0 | 0 | D5h |
| 17 | Bipiramide quadrata giroelongata |  |
Bipiramide giroelongata | 10 | 24 | 16 | 16 | 0 | 0 | 0 | 0 | 0 | D4d |
Cupole e rotonde modificate | |||||||||||||
| Jn | Nome | Immagine | Tipo | V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | Simmetria |
| 18 | Cupola triangolare elongata | 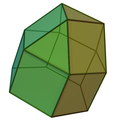 |
Cupola elongata | 15 | 27 | 14 | 4 | 9 | 0 | 1 | 0 | 0 | C3v |
| 19 | Cupola quadrata elongata | 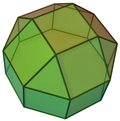 |
Cupola elongata | 20 | 36 | 18 | 4 | 13 | 0 | 0 | 1 | 0 | C4v |
| 20 | Cupola pentagonale elongata | 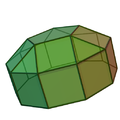 |
Cupola elongata | 25 | 45 | 22 | 5 | 15 | 1 | 0 | 0 | 1 | C5v |
| 21 | Rotonda pentagonale elongata |  |
Rotonda elongata | 30 | 55 | 27 | 10 | 10 | 6 | 0 | 0 | 1 | C5v |
| 22 | Cupola triangolare giroelongata |  |
Cupola giroelongata | 15 | 33 | 20 | 16 | 3 | 0 | 1 | 0 | 0 | C3v |
| 23 | Cupola quadrata giroelongata |  |
Cupola giroelongata | 20 | 44 | 26 | 20 | 5 | 0 | 0 | 1 | 0 | C4v |
| 24 | Cupola pentagonale giroelongata |  |
Cupola giroelongata | 25 | 55 | 32 | 25 | 5 | 1 | 0 | 0 | 1 | C5v |
| 25 | Rotonda pentagonale giroelongata |  |
Rotonda giroelongata | 30 | 65 | 37 | 30 | 0 | 6 | 0 | 0 | 1 | C5v |
| 26 | Girobifastigio |  |
Bicupola | 8 | 14 | 8 | 4 | 4 | 0 | 0 | 0 | 0 | D2d |
| 27 | Ortobicupola triangolare |  |
Bicupola | 12 | 24 | 14 | 8 | 6 | 0 | 0 | 0 | 0 | D3h |
| 28 | Ortobicupola quadrata |  |
Bicupola | 16 | 32 | 18 | 8 | 10 | 0 | 0 | 0 | 0 | D4h |
| 29 | Girobicupola quadrata |  |
Bicupola | 16 | 32 | 18 | 8 | 10 | 0 | 0 | 0 | 0 | D4d |
| 30 | Ortobicupola pentagonale | Bicupola | 20 | 40 | 22 | 10 | 10 | 2 | 0 | 0 | 0 | D5h | |
| 31 | Girobicupola pentagonale | Bicupola | 20 | 40 | 22 | 10 | 10 | 2 | 0 | 0 | 0 | D5d | |
| 32 | Ortocupolarotonda pentagonale |  |
Cupolarotonda | 25 | 50 | 27 | 15 | 5 | 7 | 0 | 0 | 0 | C5v |
| 33 | Girocupolarotonda pentagonale |  |
Cupolarotonda | 25 | 50 | 27 | 15 | 5 | 7 | 0 | 0 | 0 | C5v |
| 34 | Ortobirotonda pentagonale |  |
Birotonda | 30 | 60 | 32 | 20 | 0 | 12 | 0 | 0 | 0 | D5h |
| 35 | Ortobicupola triangolare elongata |  |
Bicupola elongata | 18 | 36 | 20 | 8 | 12 | 0 | 0 | 0 | 0 | D3h |
| 36 | Girobicupola triangolare elongata |  |
Bicupola elongata | 18 | 36 | 20 | 8 | 12 | 0 | 0 | 0 | 0 | D3d |
| 37 | Girobicupola quadrata elongata |  |
Bicupola elongata | 24 | 48 | 26 | 8 | 18 | 0 | 0 | 0 | 0 | D4d |
| 38 | Ortobicupola pentagonale elongata |  |
Bicupola elongata | 30 | 60 | 32 | 10 | 20 | 2 | 0 | 0 | 0 | D5h |
| 39 | Girobicupola pentagonale elongata |  |
Bicupola elongata | 30 | 60 | 32 | 10 | 20 | 2 | 0 | 0 | 0 | D5d |
| 40 | Ortocupolarotonda pentagonale elongata |  |
Cupolarotonda elongata | 35 | 70 | 37 | 15 | 15 | 7 | 0 | 0 | 0 | C5v |
| 41 | Girocupolarotonda pentagonale elongata | 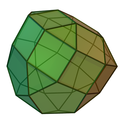 |
Cupolarotonda elongata | 35 | 70 | 37 | 15 | 15 | 7 | 0 | 0 | 0 | C5v |
| 42 | Ortobirotonda pentagonale elongata |  |
Birotonda elongata | 40 | 80 | 42 | 20 | 10 | 12 | 0 | 0 | 0 | D5h |
| 43 | Girobirotonda pentagonale elongata |  |
Birotonda elongata | 40 | 80 | 42 | 20 | 10 | 12 | 0 | 0 | 0 | D5d |
| 44 | Bicupola triangolare giroelongata | 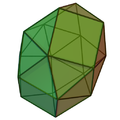 |
Bicupola giroelongata | 18 | 42 | 26 | 20 | 6 | 0 | 0 | 0 | 0 | D3 |
| 45 | Bicupola quadrata giroelongata |  |
Bicupola giroelongata | 24 | 56 | 34 | 24 | 10 | 0 | 0 | 0 | 0 | D4 |
| 46 | Bicupola pentagonale giroelongata |  |
Bicupola giroelongata | 30 | 70 | 42 | 30 | 10 | 2 | 0 | 0 | 0 | D5 |
| 47 | Cupolarotonda pentagonale giroelongata |  |
Cupolarotonda giroelongata | 35 | 80 | 47 | 35 | 5 | 7 | 0 | 0 | 0 | C5 |
| 48 | Birotonda pentagonale giroelongata |  |
Birotonda giroelongata | 40 | 90 | 52 | 40 | 0 | 12 | 0 | 0 | 0 | D5 |
Prismi aumentati | |||||||||||||
| Jn | Nome | Immagine | Tipo | V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | Simmetria |
| 49 | Prisma triangolare aumentato |  |
Prisma aumentato | 7 | 13 | 8 | 6 | 2 | 0 | 0 | 0 | 0 | C2v |
| 50 | Prisma triangolare biaumentato |  |
Prisma aumentato | 8 | 17 | 11 | 10 | 1 | 0 | 0 | 0 | 0 | C2v |
| 51 | Prisma triangolare triaumentato |  |
Prisma aumentato | 9 | 21 | 14 | 14 | 0 | 0 | 0 | 0 | 0 | D3h |
| 52 | Prisma pentagonale aumentato |  |
Prisma aumentato | 11 | 19 | 10 | 4 | 4 | 2 | 0 | 0 | 0 | C2v |
| 53 | Prisma pentagonale biaumentato |  |
Prisma aumentato | 12 | 23 | 13 | 8 | 3 | 2 | 0 | 0 | 0 | C2v |
| 54 | Prisma esagonale aumentato |  |
Prisma aumentato | 13 | 22 | 11 | 4 | 5 | 0 | 2 | 0 | 0 | C2v |
| 55 | Prisma esagonale parabiaumentato |  |
Prisma aumentato | 14 | 26 | 14 | 8 | 4 | 0 | 2 | 0 | 0 | D2h |
| 56 | Prisma esagonale metabiaumentato | 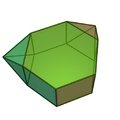 |
Prisma aumentato | 14 | 26 | 14 | 8 | 4 | 0 | 2 | 0 | 0 | C2v |
| 57 | Prisma esagonale triaumentato |  |
Prisma aumentato | 15 | 30 | 17 | 12 | 3 | 0 | 2 | 0 | 0 | D3h |
Solidi platonici modificati | |||||||||||||
| Jn | Nome | Immagine | Tipo | V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | Simmetria |
| 58 | Dodecaedro aumentato |  |
Dodecaedro aumentato | 21 | 35 | 16 | 5 | 0 | 11 | 0 | 0 | 0 | C5v |
| 59 | Dodecaedro parabiaumentato |  |
Dodecaedro aumentato | 22 | 40 | 20 | 10 | 0 | 10 | 0 | 0 | 0 | D5d |
| 60 | Dodecaedro metabiaumentato |  |
Dodecaedro aumentato | 22 | 40 | 20 | 10 | 0 | 10 | 0 | 0 | 0 | C2v |
| 61 | Dodecaedro triaumentato |  |
Dodecaedro aumentato | 23 | 45 | 24 | 15 | 0 | 9 | 0 | 0 | 0 | C3v |
| 62 | Icosaedro metabidiminuito |  |
Icosaedro diminuito | 10 | 20 | 12 | 10 | 0 | 2 | 0 | 0 | 0 | C2v |
| 63 | Icosaedro tridiminuito | 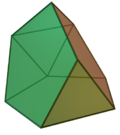 |
Icosaedro diminuito | 9 | 15 | 8 | 5 | 0 | 3 | 0 | 0 | 0 | C3v |
| 64 | Icosaedro tridiminuito aumentato |  |
- | 10 | 18 | 10 | 7 | 0 | 3 | 0 | 0 | 0 | C3v |
Solidi di Archimede modificati | |||||||||||||
| Jn | Nome | Immagine | Tipo | V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | Simmetria |
| 65 | Tetraedro troncato aumentato | 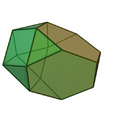 |
Tetraedro troncato aumentato | 15 | 27 | 14 | 8 | 3 | 0 | 3 | 0 | 0 | C3v |
| 66 | Cubo troncato aumentato |  |
Cubo troncato aumentato | 28 | 48 | 22 | 12 | 5 | 0 | 0 | 5 | 0 | C4v |
| 67 | Cubo troncato biaumentato |  |
Cubo troncato aumentato | 32 | 60 | 30 | 16 | 10 | 0 | 0 | 4 | 0 | D4h |
| 68 | Dodecaedro troncato aumentato |  |
Dodecaedro troncato aumentato | 65 | 105 | 42 | 25 | 5 | 1 | 0 | 0 | 11 | C5v |
| 69 | Dodecaedro troncato parabiaumentato | 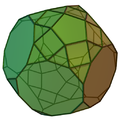 |
Dodecaedro troncato aumentato | 70 | 120 | 52 | 30 | 10 | 2 | 0 | 0 | 10 | D5d |
| 70 | Dodecaedro troncato metabiaumentato |  |
Dodecaedro troncato aumentato | 70 | 120 | 52 | 30 | 10 | 2 | 0 | 0 | 10 | C2v |
| 71 | Dodecaedro troncato triaumentato | 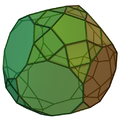 |
Dodecaedro troncato aumentato | 75 | 135 | 62 | 35 | 15 | 3 | 0 | 0 | 9 | C3v |
| 72 | Rombicosidodecaedro girato |  |
Rombicosidodecaedro girato | 60 | 120 | 62 | 20 | 30 | 12 | 0 | 0 | 0 | C5v |
| 73 | Rombicosidodecaedro parabigirato |  |
Rombicosidodecaedro girato | 60 | 120 | 62 | 20 | 30 | 12 | 0 | 0 | 0 | D5d |
| 74 | Rombicosidodecaedro metabigirato |  |
Rombicosidodecaedro girato | 60 | 120 | 62 | 20 | 30 | 12 | 0 | 0 | 0 | C2v |
| 75 | Rombicosidodecaedro trigirato |  |
Rombicosidodecaedro girato | 60 | 120 | 62 | 20 | 30 | 12 | 0 | 0 | 0 | C3v |
| 76 | Rombicosidodecaedro diminuito |  |
Rombicosidodecaedro diminuito | 55 | 105 | 52 | 15 | 25 | 11 | 0 | 0 | 1 | C5v |
| 77 | Rombicosidodecaedro paragirato diminuito |  |
Rombicosidodecaedro diminuito girato | 55 | 105 | 52 | 15 | 25 | 11 | 0 | 0 | 1 | C5v |
| 78 | Rombicosidodecaedro metagirato diminuito |  |
Rombicosidodecaedro diminuito girato | 55 | 105 | 52 | 15 | 25 | 11 | 0 | 0 | 1 | Cs |
| 79 | Rombicosidodecaedro bigirato diminuito |  |
Rombicosidodecaedro diminuito girato | 55 | 105 | 52 | 15 | 25 | 11 | 0 | 0 | 1 | Cs |
| 80 | Rombicosidodecaedro parabidiminuito | 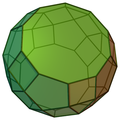 |
Rombicosidodecaedro diminuito | 50 | 90 | 42 | 10 | 20 | 10 | 0 | 0 | 2 | D5d |
| 81 | Rombicosidodecaedro metabidiminuito |  |
Rombicosidodecaedro diminuito | 50 | 90 | 42 | 10 | 20 | 10 | 0 | 0 | 2 | C2v |
| 82 | Rombicosidodecaedro bidiminuito girato |  |
Rombicosidodecaedro diminuito girato | 50 | 90 | 42 | 10 | 20 | 10 | 0 | 0 | 2 | C2v |
| 83 | Rombicosidodecaedro tridiminuito |  |
Rombicosidodecaedro diminuito | 45 | 75 | 32 | 5 | 15 | 9 | 0 | 0 | 3 | C3v |
Misti | |||||||||||||
| Jn | Nome | Immagine | Tipo | V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | Simmetria |
| 84 | Disfenoide camuso |  |
- | 8 | 18 | 12 | 12 | 0 | 0 | 0 | 0 | 0 | D2d |
| 85 | Antiprisma quadrato camuso | 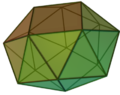 |
- | 16 | 40 | 26 | 24 | 2 | 0 | 0 | 0 | 0 | D4d |
| 86 | Sfenocorona |  |
- | 10 | 22 | 14 | 12 | 2 | 0 | 0 | 0 | 0 | C2v |
| 87 | Sfenocorona aumentata |  |
- | 11 | 26 | 17 | 16 | 1 | 0 | 0 | 0 | 0 | Cs |
| 88 | Sfenomegacorona | 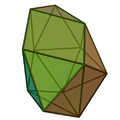 |
- | 12 | 28 | 18 | 16 | 2 | 0 | 0 | 0 | 0 | C2v |
| 89 | Ebesfenomegacorona |  |
- | 14 | 33 | 21 | 18 | 3 | 0 | 0 | 0 | 0 | C2v |
| 90 | Disfenocingolo |  |
- | 16 | 38 | 24 | 20 | 4 | 0 | 0 | 0 | 0 | D2d |
| 91 | Bilunabirotonda |  |
- | 14 | 26 | 14 | 8 | 2 | 4 | 0 | 0 | 0 | D2h |
| 92 | Ebesfenorotonda triangolare |  |
- | 18 | 36 | 20 | 13 | 3 | 3 | 1 | 0 | 0 | C3v |
Bibliografia
- Norman Johnson (1966): Convex Solids with Regular Faces, Canadian Journal of Mathematics, 18, pp. 169–200. Contiene la enumerazione originale dei 92 solidi e la congettura che non ve ne siano altri.
- Victor A. Zalgaller (1969): Convex Polyhedra with Regular Faces Consultants Bureau, New York. Traduzione dal russo: originale nei Seminari di matematica dell'istituto V.A. Steklov. Contiene la prima dimostrazione dell'esistenza di solo 92 solidi di Johnson.
Altri progetti
 Wikimedia Commons contiene immagini o altri file sul solido di Johnson
Wikimedia Commons contiene immagini o altri file sul solido di Johnson
Collegamenti esterni
- (EN) Eric W. Weisstein, Johnson Solid, su MathWorld, Wolfram Research.
- (EN) Modelli di poliedri di carta.
- (EN) Johnson Solids - Di George W. Hart.
- (EN) Johnson Polyhedra - Immagini dei 92 solidi
Wikiwand - on
Seamless Wikipedia browsing. On steroids.


