Solido platonico

In matematica, in particolare in geometria solida, il termine solido platonico, sinonimo di solido regolare e di poliedro convesso regolare, indica un poliedro convesso con le seguenti caratteristiche:

• le sue facce hanno tutte la stessa superficie, essendo poligoni regolari congruenti (cioè sovrapponibili esattamente);
• i suoi spigoli hanno tutti la stessa lunghezza;
• i suoi vertici sono tutti equivalenti, sicché i suoi angoloidi (angoli interni tridimensionali) hanno tutti la stessa ampiezza.

Vi sono in tutto cinque tipologie di solidi con queste caratteristiche:

I cinque poliedri convessi regolari (solidi platonici)
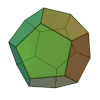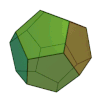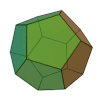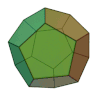
tetraedro regolare	esaedro regolare o cubo	ottaedro regolare	dodecaedro regolare	icosaedro regolare
(Modello 3D)	(Modello 3D)	(Modello 3D)	(Modello 3D)	(Modello 3D)

Il nome di ogni figura è derivata dal numero delle sue facce, rispettivamente 4, 6, 8, 12, e 20.

I cinque solidi in forma di dadi.

Storia

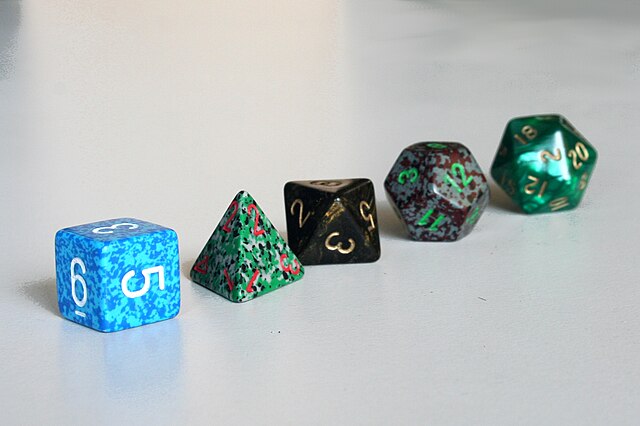
Le regolarità dei solidi platonici sono straordinariamente suggestive: questo ha fatto sì che venissero ampiamente studiati fin dall'antichità, spesso cercando in essi significati nascosti e attribuendo loro valori esoterici.

Essi furono oggetto di studio di Pitagora e Platone. Quest'ultimo, nel Timeo, associò a ognuno di essi uno dei quattro elementi: al tetraedro il fuoco, al cubo la terra, all'ottaedro l'aria, all'icosaedro l'acqua,^[1] mentre nel Fedone ritenne che il dodecaedro fosse la forma dell'universo:^[2]

«La vera terra a chi la guardi dall'alto presenta la figura di quelle palle di cuoio a dodici spicchi, variegata, distinta a colori.»

Platone rinveniva in questi solidi la presenza di una razionalità superiore nascosta nella comune realtà, assegnando loro la funzione di intermediari tra la perfezione del mondo iperuranio e la mutevolezza dei fenomeni naturali,^[3] potendo così affermare che «Dio geometrizza sempre».^[4]

A Teeteto, discepolo del matematico Teodoro e scolaro di Platone, è attribuita la dimostrazione e la costruzione dei cinque poliedri regolari e la scoperta di due di essi: l'ottaedro e l'icosaedro^[5][6].

I poliedri regolari furono poi studiati dai geometri greco-alessandrini. Le costruzioni di questi solidi sono contenute nel Libro XIII degli Elementi di Euclide.^[7] La proposizione 13 descrive la costruzione del tetraedro regolare, la proposizione 14 è dedicata all'ottaedro regolare, la proposizione 15 al cubo, la proposizione 16 all'icosaedro regolare e la proposizione 17 al dodecaedro regolare.

Il modello di Keplero del sistema solare che fa ricorso ai solidi platonici

L'interesse per i solidi platonici fu vivo anche tra matematici e artisti rinascimentali: ne studiarono le proprietà metriche Piero della Francesca (nel trattato De corporibus regularibus), Luca Pacioli (che li inserì nel suo De Divina Proportione) e successivamente Niccolò Tartaglia e Rafael Bombelli.

Pure Keplero, nella sua opera Mysterium cosmographicum, riprese, in termini diversi, l'indagine di Platone attorno al senso dei poliedri regolari nella struttura del mondo: sostenne, infatti, che i poliedri platonici fossero strettamente connessi alle armoniose proporzioni che lo caratterizzano.^[8]

«La Terra è la sfera che misura tutte le altre. Circoscrivi ad essa un dodecaedro: la sfera che lo comprende sarà Marte [nel senso che contiene l'orbita, che allora ancora riteneva circolare, del suo moto attorno al sole]. Circoscrivi a Marte un tetraedro: la sfera che lo comprende sarà Giove. Circoscrivi a Giove un cubo: la sfera che lo comprende sarà Saturno. Ora inscrivi alla Terra un icosaedro: la sfera inscritta ad essa sarà Venere. Inscrivi a Venere un ottaedro: la sfera inscritta ad essa sarà Mercurio. Hai la ragione del numero dei pianeti»

Anche l'arte presenta numerosi rinvii ai solidi platonici: tra gli esempi più celebri, vi sono Salvador Dalí (che ne fece uso in Corpus Hypercubus e nella sua Ultima Cena, ambientata proprio in un dodecaedro) e Maurits Cornelis Escher, che ne sfruttò le proprietà geometriche per eseguire alcune delle sue tassellature.

Perché sono solo cinque?

I poliedri regolari non possono essere più di cinque.

Dimostrazione con l'angoloide

{3,3} Difetto di 180°	{3,4} Difetto di 120°	{3,5} Difetto di 60°	{3,6} Difetto di 0°
{4,3} Difetto di 90°	{4,4} Difetto di 0°	{5,3} Difetto di 36°	{6,3} Difetto di 0°

Soltanto il triangolo equilatero, il quadrato e il pentagono regolare possono essere facce di poliedri regolari. La spiegazione ci viene data da Euclide negli Elementi:

1. In ciascun vertice devono convergere almeno tre facce (non esistono, infatti, angoloidi formati da uno o due poligoni).
2. In ogni angoloide la somma degli angoli delle facce che lo delimitano deve essere minore di un angolo giro, altrimenti la figura è piana; la quantità che manca per formare i 360° è definita difetto.
3. Essendo necessarie almeno tre facce per ciascun angoloide e trattandosi di poligoni regolari, ciascun vertice di ciascuna faccia può contribuire all'angoloide con massimo 360° ÷ 3 = 120°.
4. Ad avere angoli maggiori o uguali a 120° sono i poligoni con sei o più lati, pertanto possono formare solidi platonici solo il triangolo, il quadrato ed il pentagono. Ciascuna di queste figure si comporta differentemente:
   1. Facce triangolari: gli angoli di un triangolo equilatero sono ampi 60°, quindi in un vertice del solido possono insistere 3, 4, o 5 triangoli; si formano, rispettivamente, il tetraedro, l'ottaedro e l'icosaedro.
   2. Facce quadrate: gli angoli di un quadrato sono ampi 90°, è quindi possibile far incontrare in un vertice 3 facce (3 x 90 = 270) ottenendo un cubo.
   3. Facce pentagonali: ogni angolo di un pentagono regolare misura 108°. È quindi possibile far incontrare in un vertice 3 facce (3 x 108 = 324) ottenendo un dodecaedro regolare.

È in questo modo che si ottengono i cinque solidi platonici possibili.^[9]

Dimostrazione geometrica

È possibile dimostrare che non esistono più di cinque poliedri regolari anche a partire dalla relazione di Eulero. Sia dato un poliedro con F facce, ognuna delle quali è un poligono regolare con n lati e nel quale, a ogni vertice, si incontrano r spigoli, i quali sono in totale S.

Moltiplicando il numero dei lati di ogni faccia per il numero delle facce del poliedro si ottiene il doppio della totalità degli spigoli (ogni spigolo viene contato due volte, una sulla prima faccia e una sulla faccia attaccata alla prima per quello spigolo):

${\displaystyle nF=2S}$

inoltre, la totalità degli spigoli moltiplicata per due equivale al numero dei vertici V moltiplicati per il numero r di spigoli che si incontrano in essi, perché ogni spigolo collega tra loro due vertici:

${\displaystyle rV=2S}$

quindi si ottiene

${\displaystyle F={\frac {2S}{n}}}$

${\displaystyle V={\frac {2S}{r}}}$

e sostituendo questi valori nella caratteristica di Eulero-Poincaré:

${\displaystyle V+F-S=2}$

${\displaystyle {\frac {2S}{r}}+{\frac {2S}{n}}-S=2}$

e, dividendo per 2S, si arriva a

${\displaystyle {\frac {1}{r}}+{\frac {1}{n}}-{\frac {1}{2}}={\frac {1}{S}}}$

Entrambi n e r devono essere maggiori o uguali a tre, poiché un poligono deve avere almeno tre lati e almeno tre lati devono incontrarsi nel vertice di ciascuno degli angoloidi di un poliedro.

Inoltre n e r non possono essere entrambi uguali a quattro, poiché in tal caso il primo membro dell'equazione sarebbe uguale a 0, mentre 1/S è positivo. Se n e r fossero poi contemporaneamente maggiori di tre, S dovrebbe essere negativo; questa possibilità è quindi esclusa, e almeno uno deve essere tre.

Se n = 3, si ha

${\displaystyle {\frac {1}{3}}+{\frac {1}{r}}-{\frac {1}{2}}={\frac {1}{S}}}$

${\displaystyle {\frac {1}{r}}-{\frac {1}{6}}={\frac {1}{S}}}$

e quindi r può essere uguale solo a 3, 4, oppure 5, casi che corrispondono rispettivamente al tetraedro, all'ottaedro e all'icosaedro.

Allo stesso modo, se r = 3, allora n può assumere solo i valori 3, 4, oppure 5. Si può scartare 3 perché lo abbiamo considerato nel caso precedente; restano i casi 4 e 5, che corrispondono al cubo e al dodecaedro.

Non ci sono altri casi possibili, e quindi esistono al più cinque poliedri regolari.

Proprietà combinatorie

Un poliedro convesso è un solido platonico se:

1. tutte le sue facce sono poligoni regolari convessi congruenti;
2. nessuna delle sue facce interseca le altre se non negli spigoli;
3. in ogni vertice si incontrano lo stesso numero di facce.

Ogni solido platonico può essere anche connotato da una notazione {p, q} dove

p = il numero di lati di ogni faccia (o il numero di vertici di ogni faccia) e

q = il numero di facce che si incontra in ogni vertice (o il numero di spigoli che si incontrano in ogni vertice).

La sigla {p, q}, chiamata notazione di Schläfli, dà una descrizione combinatoria del poliedro. La notazione di Schläfli è esplicata nella tabella sottostante.

Poliedro		Vertici	Spigoli	Facce	Notazione di Schläfli	Posizione dei vertici
tetraedro		4	6	4	{3, 3}	3.3.3
cubo		8	12	6	{4, 3}	4.4.4
ottaedro		6	12	8	{3, 4}	3.3.3.3
dodecaedro		20	30	12	{5, 3}	5.5.5
icosaedro		12	30	20	{3, 5}	3.3.3.3.3

Proprietà metriche dei solidi platonici

La tabella seguente raggruppa alcune delle principali proprietà metriche dei solidi platonici, la misura dello spigolo di un poliedro essendo posta uguale a ${\displaystyle d}$.

Nome	Raggio della sfera			Superficie	Volume	Angolo diedro tra facce
	Inscritta	Circoscritta	Tangente gli spigoli
Tetraedro	${\displaystyle {\frac {\sqrt {6}}{12}}d}$	${\displaystyle {\frac {\sqrt {6}}{4}}d}$	${\displaystyle {\frac {\sqrt {2}}{4}}d}$	${\displaystyle {\sqrt {3}}d^{2}}$	${\displaystyle {\frac {\sqrt {2}}{12}}d^{3}}$	${\displaystyle \arctan(2{\sqrt {2}})}$
Cubo	${\displaystyle {\frac {1}{2}}d}$	${\displaystyle {\frac {\sqrt {3}}{2}}d}$	${\displaystyle {\frac {\sqrt {2}}{2}}d}$	${\displaystyle 6d^{2}}$	${\displaystyle d^{3}}$	${\displaystyle {\frac {\pi }{2}}}$
Ottaedro	${\displaystyle {\frac {\sqrt {6}}{6}}d}$	${\displaystyle {\frac {\sqrt {2}}{2}}d}$	${\displaystyle {\frac {1}{2}}d}$	${\displaystyle 2{\sqrt {3}}d^{2}}$	${\displaystyle {\frac {\sqrt {2}}{3}}d^{3}}$	${\displaystyle 2\arctan({\sqrt {2}})}$
Dodecaedro	${\displaystyle {\frac {1}{20}}{\sqrt {(10(25+11{\sqrt {5}})}}d}$	${\displaystyle {\frac {\sqrt {3}}{4}}(1+{\sqrt {5}})d}$	${\displaystyle {\frac {1}{4}}(3+{\sqrt {5}})d}$	${\displaystyle 3{\sqrt {25+10{\sqrt {5}}}}d^{2}}$	${\displaystyle {\frac {1}{4}}(15+7{\sqrt {5}})d^{3}}$
Icosaedro	${\displaystyle {\frac {\sqrt {3}}{12}}(3+{\sqrt {5}})d}$	${\displaystyle {\frac {1}{4}}{\sqrt {(10+2{\sqrt {5}})}}d}$	${\displaystyle {\frac {1}{4}}(1+{\sqrt {5}})d}$	${\displaystyle 5{\sqrt {3}}d^{2}}$	${\displaystyle {\frac {5}{12}}(3+{\sqrt {5}})d^{3}}$

Angoli fra facce poliedri regolari (utili per costruzione modelli con materiali di spessore non trascurabile)

Per cubo – soluzione banale – angolo 90°

Per gli altri poliedri la soluzione è ottenibile considerando uno dei vertici come cuspide di una piramide retta regolare che ha come base il poligono ottenuto congiungendo fra loro i vertici adiacenti a quello scelto in precedenza e valutando l’angolo β fra le altezze condotte ad un medesimo spigolo laterale di tale piramide.

Tetraedro: → β ≈ 70°,53 ≈ 70° 32’

Ottaedro: → β ≈ 109°,47 ≈ 109° 28’

Dodecaedro: → β ≈ 116°,57 ≈ 116° 34’

Icosaedro: → β ≈ 138°,19 ≈ 138° 11’

Dualità e simmetrie dei solidi platonici

La dualità poliedrale, cioè la trasfigurazione di un poliedro in un secondo poliedro che presenta rispettivamente i vertici, gli spigoli e le facce corrispondenti alle facce, agli spigoli e ai vertici del primo e che presenta le conseguenti relazioni di incidenza fra questi tre tipi di oggetti, è una involuzione che trasforma tetraedri in tetraedri e scambia cubi con ottaedri e dodecaedri con icosaedri.

L'elevata regolarità di solidi platonici si rispecchia nel fatto che ciascuno di essi ha associato un esteso gruppo di simmetria. Questi gruppi si possono considerare sottogruppi dei gruppi di simmetria dei vertici o dei gruppi di simmetria degli spigoli o dei gruppi di simmetria delle facce. I gruppi di simmetria di due solidi platonici duali sono isomorfi: infatti per dualità le permutazioni dei vertici di un poliedro diventano permutazioni delle facce del poliedro duale (mentre le permutazioni degli spigoli di un poliedro diventano permutazioni degli spigoli del duale).

Il gruppo di simmetria del tetraedro viene indicato con T_d, il gruppo di simmetria del cubo e dell'ottaedro con O_h, il gruppo di simmetria dell'icosaedro e del dodecaedro con I_h.

Solidi platonici e cristalli

Ottaedro di cristallo

Alcuni cristalli assumono la forma di solidi regolari: ad esempio il cloruro di sodio, il comune sale da cucina, si dispone in cristalli cubici, mentre il fluoruro di calcio, cioè la fluorite, si presenta in forma di ottaedri regolari.

Sono poi molti i cristalli che si dispongono seguendo composizioni e varianti dei solidi platonici; questo equivale a dire che i rispettivi reticoli cristallini presentano spiccate proprietà di simmetria. Tali proprietà hanno un ruolo fondamentale per la loro classificazione.

Note

1. Giovanni Reale, Per una nuova interpretazione di Platone, 2003, p. 678, ISBN 88-343-1036-5.
2. Platone, Fedone, 110b.
3. Vincenzo Schettino, Scienza e Arte: Chimica, arti figurative e letteratura, pag. 15, Firenze University Press, 2014.
4. Citazione attribuita a Platone da parte di Plutarco in Quaestiones convivales, VIII 2 (Moralia 718c-720c).
5. Teeteto www.treccani.it URL consultato il 20-02-2012
6. (EN) George Johnston Allman, Greek Geometry from Thales to Euclid, Hodges, Figgis, & Company, 1889, p. 206.
7. Quadrivium. Numero, geometria, musica, astronomia, Sironi Editore, 2011, p. 144, ISBN 88-518-0169-X.
8. Massimo Corradi, I Quattro Elementi: Aria, Acqua, Terra e Fuoco, 2008, p. 64, ISBN 1-4092-2642-5.
9. Solidi platonici, su gpmeneghin.com. URL consultato il 21 maggio 2016.

Voci correlate

• Geometria sacra
• Idrocarburo platonico
• Poliedro
• Poliedri di Keplero-Poinsot
• Sviluppo di solidi (geometria descrittiva)
• Solido archimedeo

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sui solidi platonici

Collegamenti esterni

• cosmici, corpi, in Dizionario di filosofia, Istituto dell'Enciclopedia Italiana, 2009.
• (EN) J.L. Heilbron, Platonic solid, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Solido platonico, su MathWorld, Wolfram Research.
• Costruzione dei 5 solidi platonici Archiviato il 14 luglio 2014 in Internet Archive. attraverso l'uso di software numerici
• Stella: Polyhedron Navigator Strumento per esplorare i poliedri
• Paper Models of Polyhedra pagina ricca di collegamenti
• Cenni di storia sui poliedri regolari (PDF), su matematica.unito.it.
• Alcune immagini di poliedri regolari, su matematita.it.
• (EN) The Uniform Polyhedra, su mathconsult.ch.
• (EN) Virtual Reality Polyhedra nella Encyclopedia of Polyhedra
• (EN) London South Bank University Struttura e comportamento dell'acqua
• (EN) Book XIII degli Elementi di Euclide

Controllo di autorità	Thesaurus BNCF 22329 · GND (DE) 4046302-3

Portale Filosofia

Portale Matematica