Tetraedro

In geometria, un tetraedro è un poliedro con quattro facce. Un tetraedro è necessariamente convesso, le sue facce sono triangolari, ha 4 vertici e 6 spigoli.

Tetraedro
Tipo	Solido platonico
Forma facce	Triangoli
Nº facce	4
Nº spigoli	6
Nº vertici	4
Valenze vertici	3
Caratteristica di Eulero	2
Incidenza dei vertici	3.3.3
Notazione di Wythoff	3 | 2 3 | 2 2 2
Notazione di Schläfli	{3,3} h{4,3}, s{2,4}, sr{2,2}
Diagramma di Coxeter-Dynkin	=
Gruppo di simmetria	Gruppo simmetrico ${\displaystyle S_{4}}$
Gruppo rotazionale	T, [3,3]+, (332)
Duale	se stesso
Angoli diedrali	circa 70° 32′
Proprietà	non chirale
Politopi correlati
Figura al vertice Poliedro duale
Sviluppo piano

Modello 3D (in formato .stl) di un tetraedro

Il tetraedro si può definire anche come simplesso tridimensionale, vale a dire come il solido tridimensionale col minor numero di vertici.

Il tetraedro regolare è uno dei cinque solidi platonici, cioè uno dei poliedri regolari e le sue facce sono triangoli equilateri. Esso presenta un angolo diedro di circa 70° 31′ 43,606″ o più precisamente di angolo diedro ${\displaystyle \textstyle \arccos {\frac {1}{3}}}$.

Parametri metrici

Alcuni parametri metrici del tetraedro regolare con spigoli di lunghezza ${\displaystyle a}$ sono i seguenti:

Altezza (cioè distanza fra vertice e faccia opposta)	${\displaystyle \,{\frac {{\sqrt {6}}a}{3}}}$
Angolo diedrale	${\displaystyle \,\arccos \left({\frac {1}{3}}\right)}$ (circa 71°)
Area della superficie totale	${\displaystyle \,a^{2}{\sqrt {3}}}$
Volume	${\displaystyle \,{\frac {1}{12}}a^{3}{\sqrt {2}}}$

La costruzione di Euclide

Fig. 1: determinazione dello spigolo ${\displaystyle AC}$ del tetraedro inscritto nella sfera di diametro ${\displaystyle AB}$

Fig. 2: costruzione del tetraedro

Nel libro XIII dei suoi Elementi, Euclide descrive il metodo per inscrivere un tetraedro regolare in una sfera di diametro dato. La costruzione descritta da Euclide è la seguente:

Sia ${\displaystyle AB}$ (vedi Fig. 1) un diametro della sfera data; lo si divida nel punto ${\displaystyle D}$ in modo che ${\displaystyle AD}$ sia il doppio di ${\displaystyle DB}$. Su questo diametro si costruisca un semicerchio, si alzi la perpendicolare da ${\displaystyle D}$ e si denoti con ${\displaystyle C}$ il punto di intersezione tra tale perpendicolare e la circonferenza. Infine, si congiungano i punti ${\displaystyle AC}$.

Si replichi la stessa costruzione su due piani passanti per ${\displaystyle AB}$, con angolo diedro di 120° rispetto al piano iniziale (Fig. 2). Si traccino infine le congiungenti fra i punti ${\displaystyle CE}$, ${\displaystyle CF}$ ed ${\displaystyle EF}$.

È chiaro che i vertici ${\displaystyle A}$, ${\displaystyle C}$, ${\displaystyle E}$ e ${\displaystyle F}$ si trovano sugli archi di cerchio costruiti sul diametro ${\displaystyle AB}$, quindi si trovano tutti sulla superficie della sfera di pari diametro. Per costruzione gli spigoli ${\displaystyle AC}$, ${\displaystyle AE}$ ed ${\displaystyle AF}$ sono uguali fra loro, così come lo sono gli spigoli ${\displaystyle CE}$, ${\displaystyle CF}$ ed ${\displaystyle EF}$ (questi ultimi determinano il triangolo equilatero alla base del tetraedro). Rimane da verificare che questi due gruppi di spigoli abbiano la stessa lunghezza.

Nella parte alta della figura di sinistra è replicata la costruzione iniziale: per il secondo teorema di Euclide, il segmento ${\displaystyle x}$ è medio proporzionale fra i segmenti ${\displaystyle AD}$ e ${\displaystyle DB}$. Supponendo (senza perdita di generalità) che il diametro del cerchio sia unitario, risulta che tali segmenti hanno le lunghezze indicate in figura, quindi:

${\displaystyle AD:x=x:DB,}$

${\displaystyle {\frac {2}{3}}:x=x:{\frac {1}{3}},}$

${\displaystyle x^{2}={\frac {2}{9}}.}$

Grazie al teorema di Pitagora si può ora calcolare la lunghezza del segmento ${\displaystyle AC}$ o, per praticità, il suo quadrato:

${\displaystyle AC^{2}=x^{2}+AD^{2}={\frac {2}{9}}+\left({\frac {2}{3}}\right)^{2}={\frac {2}{9}}+{\frac {4}{9}}={\frac {6}{9}}={\frac {2}{3}}.}$

La parte inferiore del disegno raffigura la base del tetraedro. Il segmento ${\displaystyle CF}$ è cateto del triangolo ${\displaystyle HCF}$ rettangolo in ${\displaystyle F}$, quindi:

${\displaystyle CF^{2}=HC^{2}-HF^{2}=(2x)^{2}-x^{2}=3x^{2}=3{\frac {2}{9}}={\frac {6}{9}}={\frac {2}{3}}.}$

Di conseguenza, i tre spigoli alla base del tetraedro e i tre spigoli che fanno capo al vertice ${\displaystyle A}$, hanno tutti la stessa lunghezza ${\displaystyle s=AC=CF={\sqrt {\frac {2}{3}}}}$ e quindi il poliedro costruito è effettivamente inscritto nella sfera data. Si noti inoltre come da questi calcoli segua anche che il quadrato di un qualsiasi spigolo del tetraedro è pari a ${\displaystyle \scriptstyle {\frac {2}{3}}}$ del quadrato del diametro ${\displaystyle AB}$.

Poliedro duale

Tetraedri

Il poliedro duale del tetraedro è ancora un tetraedro. Il tetraedro regolare è l'unico dei cinque solidi platonici che è duale di sé stesso: gli altri quattro sono accoppiati dalla relazione di dualità.

Simmetrie

Simmetrie del tetraedro: rotazioni intorno ad un asse o riflessione rispetto ad un piano.

Il tetraedro ha ${\displaystyle 24}$ simmetrie: ogni permutazione dei quattro vertici è infatti realizzata da un'unica simmetria. Il gruppo di simmetria è quindi il gruppo ${\displaystyle S_{4}}$ di permutazioni di ${\displaystyle 4}$ elementi, di cardinalità ${\displaystyle 4!=24}$. Tra queste, ${\displaystyle 12}$ sono rotazioni intorno ad alcuni assi, mentre le altre ${\displaystyle 12}$ invertono l'orientazione dello spazio.

Le ${\displaystyle 12}$ simmetrie rotatorie (inclusa l'identità) formano un sottogruppo, isomorfo al gruppo alternante ${\displaystyle A_{4}}$. L'asse di rotazione di una simmetria può collegare il centro di una faccia con un vertice opposto (${\displaystyle 4}$ possibilità), oppure i punti medi di due spigoli opposti (${\displaystyle 3}$ possibilità). Intorno ad un asse del primo tipo possono essere effettuate rotazioni di 120° o 240°, mentre intorno ad un asse del secondo tipo la rotazione è di 180°. In totale, si ottengono quindi ${\displaystyle 2\cdot 4+3=11}$ rotazioni, cui va aggiunta l'identità per ottenere tutte le ${\displaystyle 12}$ simmetrie rotatorie.

Le 12 simmetrie rotatorie del tetraedro. Oltre all'identità, vi sono ${\displaystyle 2\cdot 4=8}$ rotazioni lungo assi passanti per i vertici e ${\displaystyle 3}$ lungo assi che collegano spigoli opposti.

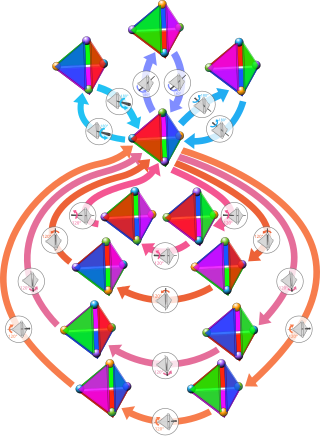
Numerando i vertici del tetraedro con ${\displaystyle 1}$, ${\displaystyle 2}$, ${\displaystyle 3}$ e ${\displaystyle 4}$, le rotazioni di 120° e 240° corrispondono alle permutazioni

${\displaystyle (123),(132),(124),(142),(134),(143),(234),(243)}$

ovvero ai cicli di ordine ${\displaystyle 3}$. Le rotazioni di 180° invece corrispondono alle permutazioni

${\displaystyle (12)(34),(13)(24),(14)(23)}$

ottenute come prodotto di ${\displaystyle 2}$-cicli indipendenti.

Delle ${\displaystyle 12}$ simmetrie che non preservano l'orientazione, ${\displaystyle 6}$ sono riflessioni lungo piani: ciascun piano contiene uno spigolo e il punto medio dello spigolo opposto (come nella figura a destra). Queste corrispondono ai cicli di ordine ${\displaystyle 2}$

${\displaystyle (12),(13),(14),(23),(24),(34)}$

Infine, le altre ${\displaystyle 6}$ simmetrie sono composizioni di riflessioni lungo piani e rotazioni, e corrispondono ai cicli di ordine ${\displaystyle 4}$

${\displaystyle (1234),(1243),(1324),(1342),(1423),(1432).}$

Generalizzazioni

Lo stesso argomento in dettaglio: Simplesso.

Il simplesso è un oggetto che generalizza la nozione di tetraedro in dimensione arbitraria. Si tratta dell'unico politopo ${\displaystyle n}$-dimensionale avente ${\displaystyle n+1}$ vertici, mentre ogni altro politopo ne ha una quantità maggiore. Per ${\displaystyle n=1,2,3}$ il simplesso è rispettivamente un segmento, un triangolo e un tetraedro.

Einstein e il tetraedro

Tetraedro costruito con sei stuzzicadenti

Esiste un curioso aneddoto riguardo Albert Einstein^[1]: ad un convegno di fisici, subissato dalle critiche per la sua balzana concezione di uno spaziotempo a quattro dimensioni, egli propose il seguente problema:

Dati sei stuzzicadenti, costruire quattro triangoli equilateri.

Nessuno dei presenti riuscì a posizionare su un piano gli stuzzicadenti per formare i triangoli richiesti, il che è infatti impossibile, al che Einstein compose un tetraedro coi sei stuzzicadenti e disse:

Se non sapete usare la terza dimensione, che sperimentate tutti i giorni, come sperate di capire la quarta?

Note

1. Maria Toffetti, Campo estivo per giovani geni, A. Mondadori, 2009.

Voci correlate

• Caleidociclo
• Solido platonico
• Teorema del tetraedro di Cauchy
• Tetraedrite

Altri progetti

Altri progetti

• Wikizionario
• Wikimedia Commons

• Wikizionario contiene il lemma di dizionario «tetraedro»
• Wikimedia Commons contiene immagini o altri file sul tetraedro

Collegamenti esterni

• Tetraedro, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
• Giovanni Sansone, TETRAEDRO, in Enciclopedia Italiana, Istituto dell'Enciclopedia Italiana, 1937.
• Tetraedro, in Dizionario delle scienze fisiche, Istituto dell'Enciclopedia Italiana, 1996.
• Tetraèdro, su Vocabolario Treccani, Istituto dell'Enciclopedia Italiana.
• tetraèdro, su sapere.it, De Agostini.
• Tetraedro, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) tetrahedron, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Tetrahedron, su MathWorld, Wolfram Research.
• (EN) Tetrahedron, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
• (EN) Poliedri uniformi, su mathconsult.ch.
• (EN) Poliedri in realtà virtuale, su georgehart.com.
• Modelli in carta di poliedri, su korthalsaltes.com.

Controllo di autorità	GND (DE) 4129555-9

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica