數學 上,一個
m
×
n
{\displaystyle m\times n}
矩陣 (英語:matrix )是一個有
m
{\displaystyle m}
n
{\displaystyle n}
矩形 陣列。矩陣裏的元素可以是數字 或符號 甚至是函數 。
[
a
11
a
12
a
13
…
a
1
j
…
a
1
n
a
21
a
22
a
23
…
a
2
j
…
a
2
n
a
31
a
32
a
33
…
a
3
j
…
a
3
n
⋮
⋮
⋮
⋱
⋮
⋱
⋮
a
i
1
a
i
2
a
i
3
…
a
i
j
…
a
i
n
⋮
⋮
⋮
⋱
⋮
⋱
⋮
a
m
1
a
m
2
a
m
3
…
a
m
j
…
a
m
n
]
{\displaystyle {\begin{bmatrix}a_{11}&a_{12}&a_{13}&\dots &a_{1j}&\dots &a_{1n}\\a_{21}&a_{22}&a_{23}&\dots &a_{2j}&\dots &a_{2n}\\a_{31}&a_{32}&a_{33}&\dots &a_{3j}&\dots &a_{3n}\\\vdots &\vdots &\vdots &\ddots &\vdots &\ddots &\vdots \\a_{i1}&a_{i2}&a_{i3}&\dots &a_{ij}&\dots &a_{in}\\\vdots &\vdots &\vdots &\ddots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&a_{m3}&\dots &a_{mj}&\dots &a_{mn}\end{bmatrix}}}
Quick Facts 線性代數, 向量 ...
線性代數
A
=
[
1
2
3
4
]
{\displaystyle \mathbf {A} ={\begin{bmatrix}1&2\\3&4\end{bmatrix}}}
向量 · 向量空間 · 基底 · 行列式 · 矩陣
Close
Quick Facts 「橫排(row)」的各地常用名稱, 中國大陸 ...
「橫排(row)」的各地常用名稱 中國大陸 行 臺灣 列
Close
Quick Facts 「縱排(column)」的各地常用名稱, 中國大陸 ...
「縱排(column)」的各地常用名稱 中國大陸 列 臺灣 行
Close
大小相同(行數列數都相同)的矩陣之間可以相互加減,具體是對每個位置上的元素做加減法。矩陣乘法 則較為複雜。兩個矩陣可以相乘,若且唯若 第一個矩陣的行數等於第二個矩陣的列數。矩陣乘法 滿足結合律 和分配律 ,但不滿足交換律 。
矩陣的一個重要用途是解線性方程組 。線性方程組中未知量的系數 可以排成一個矩陣,加上常數項,則稱為增廣矩陣。另一個重要用途是表示線性轉換 ,即是諸如
f
(
x
)
=
4
x
{\displaystyle f(x)=4x}
線性函數 的推廣。設定基底 後,某個向量
v
{\displaystyle \mathrm {v} }
m
×
1
{\displaystyle m\times 1}
f
{\displaystyle f}
m
{\displaystyle m}
A
{\displaystyle A}
f
(
v
)
{\displaystyle f(\mathrm {v} )}
A
v
{\displaystyle A\mathrm {v} }
特徵值 和特徵向量 可以揭示線性轉換的深層特性。
矩陣是高等代數學中的常見工具,也常見於統計 分析等應用數學 學科中。在物理學 中,矩陣在力學 、電路學 、光學 和量子物理 等領域中都有應用;電腦科學 中,三維動畫 製作也需要用到矩陣。矩陣的運算是數值分析 領域的重要問題。將矩陣分解 為簡單矩陣的組合可以在理論和實際應用上簡化矩陣的運算。對一些應用廣泛而形式特殊的矩陣,例如稀疏矩陣 和准對角矩陣 ,有特定的快速運算演算法 。關於矩陣相關理論的發展和應用,請參考矩陣理論 。在天體物理 、量子力學 等領域,也會出現無窮維的矩陣,是矩陣的一種推廣。
中文中矩陣的概念最早見於1922年。1922年,北京師範大學附屬中學 數學老師程廷熙 在一篇介紹文章中將矩陣譯為「縱橫陣」。1925年,在科學名詞審查會算學名詞審查組刊登於《科學》第十卷第四期的審定名詞表中,矩陣被翻譯為「矩陣式」,方塊矩陣翻譯為「方陣式」,而各類矩陣如「正交矩陣」、「伴隨矩陣」中的「矩陣」則被翻譯為「方陣」。1935年,中國數學會審查後,中華民國教育部審定的《數學名詞》(並「通令全國各院校一律遵用,以昭劃一」)中,「矩陣」作為譯名首次出現。1938年,曹惠群在接受科學名詞審查會委託就數學名詞加以校訂的《算學名詞彙編》中,認為應當的譯名是「長方陣」。1949年中華人民共和國成立後編訂的《數學名詞》中,則將譯名定為「(矩)陣」。1993年,中國自然科學名詞審定委員會 公佈的《數學名詞》中,「矩陣」被定為正式譯名,並沿用至今[ 1]
作為解決線性方程式的工具,矩陣也有不短的歷史。成書最遲在東漢 前期的《九章算術 》中,已經出現過以矩陣形式表示線性方程組系數以解方程式的圖例,可視為矩陣的雛形[ 2] 行列式 的研究發展起來後。邏輯上,矩陣的概念先於行列式,但在歷史上則恰好相反。日本數學家關孝和 (1683年)與微積分的發現者之一戈特弗里德·威廉·萊布尼茨 (1693年)近乎同時獨立建立了行列式論 。其後行列式作為解線性方程組的工具逐步發展。1750年,加布里爾·克拉默 發現了克拉瑪公式 [ 3]
阿瑟·凱萊被認為是矩陣論的奠基人 進入十九世紀後,行列式的研究進一步發展,矩陣的概念也應運而生。奧古斯丁·路易·柯西 是最早將行列式排成方陣並將其元素用雙重下標表示的數學家。他還在1829年就在行列式的框架中證明了實對稱矩陣特徵根為實數的結論[ 4] 詹姆斯·約瑟夫·西爾維斯特 注意到,在作為行列式的計算形式以外,將數以行和列的形式作出的矩形排列本身也是值得研究的。在他希望參照數的矩形陣列而又不能用行列式來形容的時候,就用「matrix」一詞來形容[ 3] 子式 ,即將矩陣的某幾行和某幾列的共同元素取出來排成的矩陣的行列式,所以實際上「matrix」被他看做是生成各種子式的「母體」:
我在先前的文章中將矩形排布的序列稱為「Matrix」,蓋因從中可以產生出各種不同的行列式,就如由同一個母體的子宮中孕育出來一樣。[ 5]
阿瑟·凱萊 被公認為矩陣論的奠基人[ 3] 數學物件 研究時,許多與矩陣有關的性質已經在行列式的研究中被發現,這也使得凱萊認為矩陣的引進是十分自然的。他說:「我決然不是通過四元數 而獲得矩陣概念的;它或是直接從行列式的概念而來,或是作為一個表達線性方程組的方便方法而來的。[ 3] [ 6] [ 7] [ 3]
此後更多數學家開始對矩陣進行研究。埃爾米特證明了如果矩陣等於其複共軛轉置,則特徵根為實數。這種矩陣後來被稱為埃爾米特矩陣[ 3] 相似矩陣 和合同矩陣 的概念。同年,他探討了矩陣的最小多項式(最小方程式)問題。1894年的論文中,他討論了矩陣理論和四元數理論的關係。1896年,他給出了凱萊-哈密爾頓定理的完整證明[ 1]
無限維矩陣的研究始於1884年。龐加萊 在兩篇不嚴謹地使用了無限維矩陣和行列式理論的文章後開始了對這一方面的專門研究[ 1] [ 1]
矩陣的定義 —
S
{\displaystyle S}
函數
A
:
{
1
,
2
,
…
,
m
}
×
{
1
,
2
,
…
,
n
}
→
S
{\displaystyle \mathbf {A} :\{1,\,2,\,\ldots ,\,m\}\times \{1,\,2,\,\ldots ,\,n\}\to S}
S
{\displaystyle S}
m
×
n
{\displaystyle m\times n}
矩陣
直觀上就是用兩個數碼去標記一堆數學實體(如數字、函數),實際上是有限序列 的一種推廣。
A
(
i
,
j
)
{\displaystyle \mathbf {A} (i,\,j)}
A
{\displaystyle \mathbf {A} }
元素 ,通常簡記為
A
i
,
j
{\displaystyle \mathbf {A} _{i,j}}
A
i
j
{\displaystyle \mathbf {A} _{ij}}
A
[
i
,
j
]
{\displaystyle \mathbf {A} _{[i,j]}}
a
i
j
{\displaystyle \mathrm {a} _{ij}}
A
{\displaystyle \mathbf {A} }
A
{\displaystyle \mathbf {A} }
a
i
j
{\displaystyle \mathrm {a} _{ij}}
A
{\displaystyle \mathbf {A} }
A
=
[
a
i
j
]
m
×
n
{\displaystyle \mathbf {A} =[\mathrm {a} _{ij}]_{m\times n}}
A
=
[
a
i
,
j
]
m
×
n
{\displaystyle \mathbf {A} =[\mathrm {a} _{i,\,j}]_{m\times n}}
如果表達式
f
(
i
,
j
)
=
T
(
i
,
j
)
{\displaystyle f(i,\,j)=T(i,j)}
合式公式 ,其中
T
{\displaystyle T}
T
(
i
,
j
)
{\displaystyle T(i,\,j)}
項 )可以唯一決定一個矩陣
A
{\displaystyle \mathbf {A} }
A
=
[
T
(
i
,
j
)
]
m
×
n
{\displaystyle \mathbf {A} =[T(i,\,j)]_{m\times n}}
A
:
{
1
,
2
,
…
,
m
}
×
{
1
,
2
,
…
,
n
}
→
N
{\displaystyle \mathbf {A} :\{1,\,2,\,\ldots ,\,m\}\times \{1,\,2,\,\ldots ,\,n\}\to \mathbb {N} }
A
(
i
,
j
)
=
i
+
j
{\displaystyle \mathbf {A} (i,\,j)=i+j}
就可以表達為
A
=
[
i
+
j
]
m
×
n
{\displaystyle \mathbf {A} =[i+j]_{m\times n}}
根據公理化集合論 ,可以定義一個函數的集合
S
m
×
n
{\displaystyle S^{m\times n}}
S
{\displaystyle S}
m
×
n
{\displaystyle m\times n}
S
m
×
n
:=
{
f
|
f
:
{
1
,
2
,
…
,
m
}
×
{
1
,
2
,
…
,
n
}
→
S
}
{\displaystyle S^{m\times n}:=\left\{f\,|\,f:\{1,\,2,\,\ldots ,\,m\}\times \{1,\,2,\,\ldots ,\,n\}\to S\right\}}
以下的
3
×
2
{\displaystyle 3\times 2}
{
(
(
1
,
1
)
,
a
)
,
(
(
1
,
2
)
,
b
)
,
(
(
2
,
1
)
,
c
)
,
(
(
2
,
2
)
,
d
)
,
(
(
2
,
2
)
,
e
)
,
(
(
2
,
2
)
,
f
)
}
{\displaystyle \left\{\left((1,\,1),\,a\right),\,\left((1,\,2),\,b\right),\,\left((2,\,1),\,c\right),\,\left((2,\,2),\,d\right),\,\left((2,\,2),\,e\right),\,\left((2,\,2),\,f\right)\right\}}
一般會如下排列成為矩形來表示:
[
a
b
c
d
e
f
]
{\displaystyle {\begin{bmatrix}a&b\\c&d\\e&f\end{bmatrix}}}
英文將橫向的元素組統稱為「row 」,縱向統稱為「column 」;但兩岸對此卻以不同的稱呼;在中國大陸 ,橫向的元素組稱為「行」,縱向稱為「列」,而在臺灣 則相反,橫向稱為「列」,縱向稱為「行」[ 8]
行數是1或列數是1的矩陣又可分別稱為行向量 和列向量 維 的情況下,向量 可用其分量表示成行數或列數是1的矩陣。
矩陣的最基本運算包括矩陣加(減)法,實數積和轉置運算。被稱為「矩陣加法」、「實數積」和「轉置」的運算不止一種[ 9]
More information
運算
定義
例子
加(減)法
m
×
n
{\displaystyle m\times n}
A
{\displaystyle \mathbf {A} }
B
{\displaystyle \mathbf {B} }
A
±
B
{\displaystyle \mathbf {A} \pm \mathbf {B} }
m
×
n
{\displaystyle m\times n}
A
{\displaystyle \mathbf {A} }
B
{\displaystyle \mathbf {B} }
(
A
±
B
)
i
,
j
=
A
i
,
j
±
B
i
,
j
{\displaystyle (\mathbf {A} \pm \mathbf {B} )_{i,j}=\mathbf {A} _{i,j}\pm \mathbf {B} _{i,j}}
其中
1
≤
i
≤
m
,
1
≤
j
≤
n
{\displaystyle 1\leq i\leq m,1\leq j\leq n}
[
1
3
1
1
0
0
]
+
[
0
0
5
7
5
0
]
=
[
1
+
0
3
+
0
1
+
5
1
+
7
0
+
5
0
+
0
]
=
[
1
3
6
8
5
0
]
{\displaystyle {\begin{bmatrix}1&3&1\\1&0&0\end{bmatrix}}+{\begin{bmatrix}0&0&5\\7&5&0\end{bmatrix}}={\begin{bmatrix}1+0&3+0&1+5\\1+7&0+5&0+0\end{bmatrix}}={\begin{bmatrix}1&3&6\\8&5&0\end{bmatrix}}}
實數積
純量
c
{\displaystyle c}
A
{\displaystyle \mathbf {A} }
c
A
{\displaystyle c\mathbf {A} }
A
{\displaystyle \mathbf {A} }
c
{\displaystyle c}
(
c
A
)
i
,
j
=
c
⋅
A
i
,
j
{\displaystyle (c\mathbf {A} )_{i,j}=c\cdot \mathbf {A} _{i,j}}
2
⋅
[
1
8
−
3
4
−
2
5
]
=
[
2
⋅
1
2
⋅
8
2
⋅
(
−
3
)
2
⋅
4
2
⋅
(
−
2
)
2
⋅
5
]
=
[
2
16
−
6
8
−
4
10
]
{\displaystyle 2\cdot {\begin{bmatrix}1&8&-3\\4&-2&5\end{bmatrix}}={\begin{bmatrix}2\cdot 1&2\cdot 8&2\cdot (-3)\\2\cdot 4&2\cdot (-2)&2\cdot 5\end{bmatrix}}={\begin{bmatrix}2&16&-6\\8&-4&10\end{bmatrix}}}
轉置
m
×
n
{\displaystyle m\times n}
A
{\displaystyle \mathbf {A} }
n
×
m
{\displaystyle n\times m}
A
T
{\displaystyle \mathbf {A} ^{\mathrm {T} }}
A
t
r
{\displaystyle \mathbf {A} ^{\mathrm {tr} }}
t
A
{\displaystyle ^{\mathrm {t} }\mathbf {A} }
A
′
{\displaystyle \mathbf {A} '}
i
{\displaystyle i}
A
{\displaystyle \mathbf {A} }
i
{\displaystyle i}
A
T
{\displaystyle \mathbf {A} ^{\mathrm {T} }}
i
{\displaystyle i}
j
{\displaystyle j}
A
{\displaystyle \mathbf {A} }
j
{\displaystyle j}
i
{\displaystyle i}
(
A
T
)
i
,
j
=
A
j
,
i
{\displaystyle (\mathbf {A} ^{\mathrm {T} })_{i,j}=\mathbf {A} _{j,i}}
[
1
2
3
0
−
6
7
]
T
=
[
1
0
2
−
6
3
7
]
{\displaystyle {\begin{bmatrix}1&2&3\\0&-6&7\end{bmatrix}}^{T}={\begin{bmatrix}1&0\\2&-6\\3&7\end{bmatrix}}}
Close
矩陣的加法運算滿足交換律:
A
+
B
=
B
+
A
{\displaystyle \mathbf {A} +\mathbf {B} =\mathbf {B} +\mathbf {A} }
[ 10]
(
A
+
B
)
T
=
A
T
+
B
T
{\displaystyle (\mathbf {A} +\mathbf {B} )^{\mathrm {T} }=\mathbf {A} ^{\mathrm {T} }+\mathbf {B} ^{\mathrm {T} }}
c
(
A
+
B
)
=
c
A
+
c
B
{\displaystyle c(\mathbf {A} +\mathbf {B} )=c\mathbf {A} +c\mathbf {B} }
矩陣加法和實數積兩種運算使得
M
(
m
,
n
,
R
)
{\displaystyle {\mathcal {M}}(m,n,\mathbb {R} )}
m
n
{\displaystyle mn}
線性空間 。而轉置和實數積運算滿足類似於結合律的規律:
c
(
A
T
)
=
c
(
A
)
T
{\displaystyle c(\mathbf {A} ^{\mathrm {T} })=c(\mathbf {A} )^{\mathrm {T} }}
矩陣也有類似行列式的初等轉換 ,即對矩陣的某些行和某些列進行三類操作:交換兩行/列,將一行/列的每個元素都乘以一個固定的量,以及將一行/列的每個元素乘以一個固定的量之後加到另一行/列的相應元素上。這些操作在求其逆矩陣 時有用。
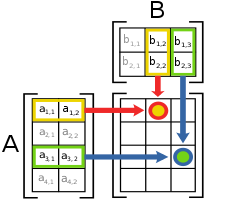
矩陣A B AB 兩個矩陣的乘法僅當第一個矩陣
A
{\displaystyle \mathbf {A} }
B
{\displaystyle \mathbf {B} }
A
{\displaystyle \mathbf {A} }
m
×
n
{\displaystyle m\times n}
B
{\displaystyle \mathbf {B} }
n
×
p
{\displaystyle n\times p}
乘積
A
B
{\displaystyle \mathbf {AB} }
m
×
p
{\displaystyle m\times p}
[
A
B
]
i
,
j
=
A
i
,
1
B
1
,
j
+
A
i
,
2
B
2
,
j
+
⋯
+
A
i
,
n
B
n
,
j
=
∑
r
=
1
n
A
i
,
r
B
r
,
j
{\displaystyle [\mathbf {AB} ]_{i,j}=A_{i,1}B_{1,j}+A_{i,2}B_{2,j}+\cdots +A_{i,n}B_{n,j}=\sum _{r=1}^{n}A_{i,r}B_{r,j}}
其中
1
≤
i
≤
m
,
1
≤
j
≤
p
′
{\displaystyle 1\leq i\leq m,\ 1\leq j\leq p'}
[ 11]
例如
[
1
0
2
−
1
3
1
]
×
[
3
1
2
1
1
0
]
=
[
(
1
×
3
+
0
×
2
+
2
×
1
)
(
1
×
1
+
0
×
1
+
2
×
0
)
(
−
1
×
3
+
3
×
2
+
1
×
1
)
(
−
1
×
1
+
3
×
1
+
1
×
0
)
]
=
[
5
1
4
2
]
{\displaystyle {\begin{bmatrix}1&0&2\\-1&3&1\\\end{bmatrix}}\times {\begin{bmatrix}3&1\\2&1\\1&0\end{bmatrix}}={\begin{bmatrix}(1\times 3+0\times 2+2\times 1)&(1\times 1+0\times 1+2\times 0)\\(-1\times 3+3\times 2+1\times 1)&(-1\times 1+3\times 1+1\times 0)\\\end{bmatrix}}={\begin{bmatrix}5&1\\4&2\\\end{bmatrix}}}
矩陣的乘法滿足結合律和對矩陣加法的分配律(左分配律和右分配律):
結合律:
(
A
B
)
C
=
A
(
B
C
)
{\displaystyle (\mathbf {AB} )\mathbf {C} =\mathbf {A} (\mathbf {BC} )}
左分配律:
(
A
+
B
)
C
=
A
C
+
B
C
{\displaystyle (\mathbf {A} +\mathbf {B} )\mathbf {C} =\mathbf {AC} +\mathbf {BC} }
右分配律:
C
(
A
+
B
)
=
C
A
+
C
B
{\displaystyle \mathbf {C} (\mathbf {A} +\mathbf {B} )=\mathbf {CA} +\mathbf {CB} }
矩陣的乘法與實數積運算之間也滿足類似結合律的規律;與轉置之間則滿足倒置的分配律。
c
(
A
B
)
=
(
c
A
)
B
=
A
(
c
B
)
{\displaystyle c(\mathbf {AB} )=(c\mathbf {A} )\mathbf {B} =\mathbf {A} (c\mathbf {B} )}
(
A
B
)
T
=
B
T
A
T
{\displaystyle (\mathbf {AB} )^{\mathrm {T} }=\mathbf {B} ^{\mathrm {T} }\mathbf {A} ^{\mathrm {T} }}
矩陣乘法不滿足 交換律 。一般來說,矩陣
A
{\displaystyle \mathbf {A} }
B
{\displaystyle \mathbf {B} }
A
B
{\displaystyle \mathbf {AB} }
B
A
{\displaystyle \mathbf {BA} }
A
B
≠
B
A
{\displaystyle \mathbf {AB} \neq \mathbf {BA} }
[
1
2
3
4
]
[
0
1
0
0
]
=
[
0
1
0
3
]
,
[
0
1
0
0
]
[
1
2
3
4
]
=
[
3
4
0
0
]
{\displaystyle {\begin{bmatrix}1&2\\3&4\\\end{bmatrix}}{\begin{bmatrix}0&1\\0&0\\\end{bmatrix}}={\begin{bmatrix}0&1\\0&3\\\end{bmatrix}},\qquad \quad {\begin{bmatrix}0&1\\0&0\\\end{bmatrix}}{\begin{bmatrix}1&2\\3&4\\\end{bmatrix}}={\begin{bmatrix}3&4\\0&0\\\end{bmatrix}}}
。
這一特性使得矩陣代數與常見的一些數體 (有理數、實數、複數)以及環(多項式環 、整數環)都不同。給定一個
n
{\displaystyle n}
A
{\displaystyle \mathbf {A} }
A
{\displaystyle \mathbf {A} }
A
{\displaystyle \mathbf {A} }
M
(
n
,
R
)
{\displaystyle {\mathcal {M}}(n,\mathbb {R} )}
A
{\displaystyle \mathbf {A} }
[ 12]
M
(
n
,
R
)
{\displaystyle {\mathcal {M}}(n,\mathbb {R} )}
λ
I
n
,
λ
∈
R
{\displaystyle \lambda \mathbf {I} _{n},\,\lambda \in \mathbb {R} }
I
n
{\displaystyle \mathbf {I} _{n}}
單位矩陣 ,也就是主對角線上的元素為1,其它元素為0的矩陣。任意矩陣
M
{\displaystyle \mathbf {M} }
M
I
n
=
M
=
I
n
M
{\displaystyle \mathbf {M} \mathbf {I} _{n}=\mathbf {M} =\mathbf {I} _{n}\mathbf {M} }
除了最常見的矩陣乘法定義以外,也有一些較不常見的矩陣乘法,比如阿達馬乘積 和克羅內克乘積 [ 13]
矩陣乘法的一個基本應用是線上性方程組上。線性方程組是方程組 的一種,它符合以下的形式:
{
a
1
,
1
x
1
+
a
1
,
2
x
2
+
⋯
+
a
1
,
n
x
n
=
b
1
a
2
,
1
x
1
+
a
2
,
2
x
2
+
⋯
+
a
2
,
n
x
n
=
b
2
⋮
⋮
a
m
,
1
x
1
+
a
m
,
2
x
2
+
⋯
+
a
m
,
n
x
n
=
b
m
{\displaystyle {\begin{cases}a_{1,1}x_{1}+a_{1,2}x_{2}+\cdots +a_{1,n}x_{n}=b_{1}\\a_{2,1}x_{1}+a_{2,2}x_{2}+\cdots +a_{2,n}x_{n}=b_{2}\\\vdots \quad \quad \quad \vdots \\a_{m,1}x_{1}+a_{m,2}x_{2}+\cdots +a_{m,n}x_{n}=b_{m}\end{cases}}}
其中的
a
1
,
1
,
a
1
,
2
{\displaystyle a_{1,1},\,a_{1,2}}
b
1
,
b
2
{\displaystyle b_{1},\,b_{2}}
x
1
,
x
2
{\displaystyle x_{1},\,x_{2}}
A
x
=
b
{\displaystyle \mathbf {A} \mathbf {x} =\mathbf {b} }
其中,
A
{\displaystyle \mathbf {A} }
m
×
n
{\displaystyle m\times n}
矩陣 ,
x
{\displaystyle \mathbf {x} }
n
{\displaystyle n}
b
{\displaystyle \mathbf {b} }
m
{\displaystyle m}
[ 14]
A
=
[
a
1
,
1
a
1
,
2
⋯
a
1
,
n
a
2
,
1
a
2
,
2
⋯
a
2
,
n
⋮
⋮
⋱
⋮
a
m
,
1
a
m
,
2
⋯
a
m
,
n
]
,
x
=
[
x
1
x
2
⋮
x
n
]
,
b
=
[
b
1
b
2
⋮
b
m
]
{\displaystyle \mathbf {A} ={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{m,1}&a_{m,2}&\cdots &a_{m,n}\end{bmatrix}},\quad \mathbf {x} ={\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix}},\quad \mathbf {b} ={\begin{bmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{bmatrix}}}
這個寫法下,將原來的多個方程式轉化成一個向量方程式,在已知矩陣
A
{\displaystyle \mathbf {A} }
b
{\displaystyle \mathbf {b} }
x
{\displaystyle \mathbf {x} }
矩陣是線性轉換的便利表達法。矩陣乘法的本質在聯絡到線性轉換的時候最能體現,因為矩陣乘法和線性轉換的合成有以下的聯絡:
以
R
n
{\displaystyle \mathbb {R} ^{n}}
n
{\displaystyle n}
m
×
n
{\displaystyle m\times n}
A
{\displaystyle \mathbf {A} }
R
n
{\displaystyle \mathbb {R} ^{n}}
R
m
{\displaystyle \mathbb {R} ^{m}}
f
:
R
n
→
R
m
{\displaystyle f:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}}
m ×n
A
f
{\displaystyle \mathbf {A} _{f}}
R
n
{\displaystyle \mathbb {R} ^{n}}
x
{\displaystyle x}
f
(
x
)
=
A
f
x
{\displaystyle f(x)=A_{f}x}
A
f
{\displaystyle \mathbf {A} _{f}}
i
{\displaystyle i}
j
{\displaystyle j}
正則基 向量
e
j
=
(
0
,
⋯
,
0
,
1
,
0
,
⋯
0
)
T
{\displaystyle \mathbf {e} _{j}=(0,\cdots ,0,1,0,\cdots 0)^{T}}
j
f
{\displaystyle f}
f
(
e
j
)
{\displaystyle f(\mathbf {e} _{j})}
i
{\displaystyle i}
也就是說,從
R
n
{\displaystyle \mathbb {R} ^{n}}
R
m
{\displaystyle \mathbb {R} ^{m}}
L
(
R
n
,
R
m
)
{\displaystyle {\mathcal {L}}\left(\mathbb {R} ^{n},\mathbb {R} ^{m}\right)}
M
(
m
,
n
,
R
)
{\displaystyle {\mathcal {M}}(m,n,\mathbb {R} )}
一一對映 :
f
↦
A
f
{\displaystyle f\mapsto A_{f}}
以下是一些典型的2維實平面上的線性轉換對平面向量(圖形)造成的效果,以及它們對應的2維矩陣。其中每個線性轉換將藍色圖形對映成綠色圖形;平面的原點(0, 0)用黑點表示。
推移 ,水平鏡射 轉換
「擠壓 」轉換,
伸縮 ,3/2倍
旋轉 ,左轉30°
[
1
1.25
0
1
]
{\displaystyle {\begin{bmatrix}1&1.25\\0&1\end{bmatrix}}}
[
−
1
0
0
1
]
{\displaystyle {\begin{bmatrix}-1&0\\0&1\end{bmatrix}}}
[
3
2
0
0
2
3
]
{\displaystyle {\begin{bmatrix}{\frac {3}{2}}&0\\0&{\frac {2}{3}}\end{bmatrix}}}
[
3
2
0
0
3
2
]
{\displaystyle {\begin{bmatrix}{\frac {3}{2}}&0\\0&{\frac {3}{2}}\end{bmatrix}}}
[
cos
(
π
6
)
−
sin
(
π
6
)
sin
(
π
6
)
cos
(
π
6
)
]
{\displaystyle {\begin{bmatrix}\cos({\frac {\pi }{6}})&-\sin({\frac {\pi }{6}})\\\sin({\frac {\pi }{6}})&\cos({\frac {\pi }{6}})\end{bmatrix}}}
設有
k
×
m
{\displaystyle k\times m}
B
{\displaystyle \mathbf {B} }
g
:
R
m
→
R
k
{\displaystyle g:\mathbf {R} ^{m}\rightarrow \mathbf {R} ^{k}}
B
A
{\displaystyle \mathbf {BA} }
g
∘
f
{\displaystyle g\circ f}
[ 15]
(
g
∘
f
)
(
x
)
=
g
(
f
(
x
)
)
=
g
(
A
x
)
=
B
(
A
x
)
=
(
B
A
)
x
{\displaystyle (g\circ f)(x)=g(f(x))=g(\mathbf {Ax} )=\mathbf {B} (\mathbf {Ax} )=(\mathbf {BA} )\mathbf {x} }
矩陣的秩 是指矩陣中線性無關 的行/列向量的最大個數[ 16] 像空間 的維度[ 17] 秩-零化度定理 說明矩陣的行數量等於矩陣的秩與零空間 維度之和[ 18]
矩陣的元素除了可以是實數和複數以外,也可以任意環或體 中元素。線上性代數中,矩陣的性質可以經由有限維的線性空間中的線性轉換定義。更廣泛的,無限維空間中的線性算子 ,則可以定義更廣泛的無窮維矩陣。矩陣的另一種推廣是張量 。純量可以看成零維方式排列的數據(只有一個「點」),向量可以看成是一維方式排列的數據(若干個「點」排成的「線段」),矩陣可以看成是二維方式排列的數據(若干個「線段」排成的「矩形」),而張量的概念則包括了這幾種排列方式。在張量的概念中,純量是零維張量,向量是一維張量,矩陣是二維張量,而更高維方式排列的數據方式就是高維張量[ 46]
矩陣的元素除了可以是實數和複數以外,還可以是任何能夠使得矩陣的運算律成立的元素。首先,矩陣的元素可以是任意一個體(即能夠進行「加減乘除」運算的集合)中元素。例如編碼理論 中會出現系數為有限體 中元素的矩陣,以及有理數系數的矩陣。如果矩陣的系數所在體
K
{\displaystyle \mathbf {K} }
代數閉體 ,那麼在求矩陣的特徵值時,由於特徵值是相應的特徵多項式的根,可能不在系數體
K
{\displaystyle \mathbf {K} }
L 中。反過來,如果考慮擴張體
L
/
K
{\displaystyle \mathbf {L/K} }
,以及
L
{\displaystyle \mathbf {L} }
α
{\displaystyle \alpha }
L
{\displaystyle \mathbf {L} }
m
α
:
x
↦
α
x
{\displaystyle m_{\alpha }:\,x\mapsto \alpha x}
m
α
{\displaystyle m_{\alpha }}
K
{\displaystyle \mathbf {K} }
n
×
n
{\displaystyle n\times n}
K
{\displaystyle \mathbf {K} }
X
α
{\displaystyle X_{\alpha }}
n
{\displaystyle n}
L
/
K
{\displaystyle \mathbf {L/K} }
α
{\displaystyle \alpha }
p
X
α
{\displaystyle p_{X_{\alpha }}}
α
{\displaystyle \alpha }
K
{\displaystyle \mathbf {K} }
最小多項式
min
K
(
α
)
{\displaystyle \operatorname {min} _{\mathbf {K} }(\alpha )}
p
X
α
=
(
min
K
(
α
)
)
r
{\displaystyle p_{X_{\alpha }}=\left(\operatorname {min} _{\mathbf {K} }(\alpha )\right)^{r}\,}
r
{\displaystyle r}
L
/
K
{\displaystyle \mathbf {L/K} }
(
α
)
{\displaystyle (\alpha )}
[ 47] 更一般的情況是矩陣的元素屬於某個環
R
{\displaystyle \mathbf {R} }
[ 48]
R
{\displaystyle \mathbf {R} }
M
(
m
,
n
,
R
)
{\displaystyle {\mathcal {M}}(m,n,\mathbf {R} )}
M
(
m
,
n
,
R
)
{\displaystyle {\mathcal {M}}(m,n,\mathbf {R} )}
矩陣環 。
n
{\displaystyle n}
M
(
n
,
R
)
{\displaystyle {\mathcal {M}}(n,\mathbf {R} )}
R
{\displaystyle \mathbf {R} }
模
R
n
{\displaystyle \mathbf {R} ^{n}}
的自同態 環同構 [ 49]
若
R
{\displaystyle \mathbf {R} }
交換環 ,則
M
(
m
,
R
)
{\displaystyle {\mathcal {M}}(m,\mathbf {R} )}
單位元 的
R
{\displaystyle \mathbf {R} }
代數 ,滿足結合律,但不滿足交換律。其中的矩陣仍然可以用萊布尼茲公式定義行列式 。一個矩陣可逆若且唯若其行列式為環
R
{\displaystyle \mathbf {R} }
可逆元素 (體上的矩陣可逆只需行列式不等於0)[ 50]
前面已經提到,所有
R
n
→
R
m
{\displaystyle \mathbf {R} ^{n}\rightarrow \mathbf {R} ^{m}}
M
(
m
,
n
,
R
)
{\displaystyle {\mathcal {M}}(m,n,\mathbf {R} )}
f
:
V
→
W
{\displaystyle f:\mathbf {V} \rightarrow \mathbf {W} }
A
f
=
(
a
i
j
)
{\displaystyle \mathbf {A} _{f}=(a_{ij})}
V
{\displaystyle \mathbf {V} }
W
{\displaystyle \mathbf {W} }
v
1
,
…
,
v
n
{\displaystyle \mathbf {v} _{1},\ldots ,\mathbf {v} _{n}}
w
1
,
…
,
w
m
{\displaystyle \mathbf {w} _{1},\ldots ,\mathbf {w} _{m}}
對任意
j
=
1
,
…
,
n
{\displaystyle j=1,\ldots ,n}
f
(
v
j
)
=
∑
i
=
1
m
a
i
,
j
w
i
{\displaystyle f(\mathbf {v} _{j})=\sum _{i=1}^{m}a_{i,j}\mathbf {w} _{i}}
矩陣
A
f
{\displaystyle \mathbf {A} _{f}}
V
{\displaystyle \mathbf {V} }
W
{\displaystyle \mathbf {W} }
(
w
1
,
…
,
w
m
)
{\displaystyle (\mathbf {w} _{1},\ldots ,\mathbf {w} _{m})}
f 在特定「角度」(基底)下的「素描」。不同的「角度」下,描述
f
{\displaystyle f}
相似矩陣 [ 51] f 的對偶轉換
f
∗
:
W
∗
→
V
∗
{\displaystyle f^{*}:\mathbf {W} ^{*}\rightarrow \mathbf {V} ^{*}}
[ 52]
當矩陣的元素是帶單位元的環
R
{\displaystyle \mathbf {R} }
m
×
n
{\displaystyle m\times n}
R
{\displaystyle \mathbf {R} }
R
{\displaystyle \mathbf {R} }
自由模
R
m
{\displaystyle \mathbf {R} ^{m}}
和
R
n
{\displaystyle \mathbf {R} ^{n}}
R
{\displaystyle \mathbf {R} }
n
=
m
{\displaystyle n=m}
R
{\displaystyle \mathbf {R} }
n
{\displaystyle n}
R
{\displaystyle \mathbf {R} }
R
{\displaystyle \mathbf {R} }
R
n
{\displaystyle \mathbf {R} ^{n}}
主條目:無限維矩陣
無窮維矩陣可以指行數或列數無窮大,或兩者都是無窮大的矩陣[ 58] 可數集 。需要注意的是,無窮維矩陣的乘法涉及到無窮級數 求和,因此只有在相關的無窮級數收斂 的時候,才能定義矩陣的乘積[ 59]
N
×
N
{\displaystyle \mathbb {N} \times \mathbb {N} }
[ 60]
無限矩陣無法定義通常意義上的行列式,因此可逆矩陣不一定是方塊矩陣,同理,么正矩陣也不一定要是方塊矩陣[ 61]
分塊矩陣
P
=
[
1
2
3
2
1
2
7
5
4
9
2
6
6
1
5
8
]
{\displaystyle P={\begin{bmatrix}1&2&3&2\\1&2&7&5\\4&9&2&6\\6&1&5&8\end{bmatrix}}}
可分割成4個2×2的矩陣
P
11
=
[
1
2
1
2
]
,
P
12
=
[
3
2
7
5
]
,
P
21
=
[
4
9
6
1
]
,
P
22
=
[
2
6
5
8
]
{\displaystyle P_{11}={\begin{bmatrix}1&2\\1&2\end{bmatrix}},P_{12}={\begin{bmatrix}3&2\\7&5\end{bmatrix}},P_{21}={\begin{bmatrix}4&9\\6&1\end{bmatrix}},P_{22}={\begin{bmatrix}2&6\\5&8\end{bmatrix}}}
P
=
[
P
11
P
12
P
21
P
22
]
{\displaystyle P={\begin{bmatrix}P_{11}&P_{12}\\P_{21}&P_{22}\end{bmatrix}}}
[ 65]
矩陣在許多領域都應用廣泛。有些時候用到矩陣是因為其表達方式緊湊,例如在博弈論 和經濟學 中,會用收益矩陣 來表示兩個博弈物件在各種決策方式下的收益[ 66] 文字挖掘 和索引典 組譯的時候,比如在TF-IDF 方法中,也會用到檔案項矩陣 來追蹤特定詞彙在多個檔案中的出現頻率[ 67]
複數可以用實系數的2×2矩陣表示:
a
+
i
b
↔
[
a
−
b
b
a
]
,
{\displaystyle a+ib\leftrightarrow {\begin{bmatrix}a&-b\\b&a\end{bmatrix}},}
這種表示法與複數的加減法、乘法都相容。比如,2×2的旋轉矩陣可以用來表示模長為1的複數,一個向量乘以此旋轉矩陣可以視作一個複數乘以該模長為1的複數。對四元數 也有類似的矩陣表達[ 68]
早期的密碼 技術如希爾密碼 也用到矩陣。然而,矩陣的線性性質使這類密碼相對容易破解[ 69] 電腦圖像處理 也會用到矩陣來表示處理物件,並且用放射旋轉矩陣來計算物件的轉換,實現三維物件在特定二維螢幕上的投影[ 70] 多項式環 上的矩陣在控制論 中有重要作用。
化學 中也有矩陣的應用,特別在使用量子理論 討論分子鍵 和光譜 的時候。具體例子有解羅特漢方程式 時用重疊矩陣 和福柯矩陣 來得到哈特里-福克 方法中的分子軌道 。
在多元函數微積分學中,對二階偏導數存在的函數
f
:
R
n
→
R
{\displaystyle f:\mathbf {R} ^{n}\rightarrow \mathbf {R} }
海森矩陣 [ 73]
H
(
f
)
(
x
)
=
[
∂
2
f
∂
x
i
∂
x
j
(
x
)
]
{\displaystyle H(f)(x)=\left[{\frac {\partial ^{2}f}{\partial x_{i}\,\partial x_{j}}}(x)\right]}
n
=
2
{\displaystyle n=2}
[
2
0
0
−
2
]
{\displaystyle {\begin{bmatrix}2&0\\0&-2\end{bmatrix}}}
f
(
x
,
y
)
=
x
2
−
y
2
{\displaystyle f(x,y)=x^{2}-y^{2}}
(
x
=
0
,
y
=
0
)
{\displaystyle (x=0,y=0)}
鞍點 (紅色點)嚴格來說,僅當函數在某一點上的二階偏導數存在,才能定義這一點上的海森矩陣。海森矩陣給出了函數在這一點的變化率方面的資訊。當給定的點
x
=
(
x
1
,
…
,
x
n
)
{\displaystyle \mathbf {x} =(x_{1},\ldots ,x_{n})}
平穩點 (即函數
f
{\displaystyle f}
∂
f
∂
x
i
{\displaystyle {\frac {\partial f}{\partial x_{i}}}}
x
{\displaystyle \mathbf {x} }
泰勒展開 是:
f
(
x
+
h
)
=
f
(
x
)
+
∇
f
(
x
)
⋅
h
+
1
2
h
T
H
(
f
)
(
x
)
h
+
∘
(
‖
x
‖
3
)
{\displaystyle f(x+h)=f(x)+\nabla f(x)\cdot h+{\frac {1}{2}}h^{T}H(f)(x)h+\circ \left(\|x\|^{3}\right)}
如果函數在點x 的一階偏導數都是0,那麼
∇
f
=
0
{\displaystyle \nabla f=0}
x 附近的變化率取決於海森矩陣
H
(
f
)
(
x
)
{\displaystyle H(f)(x)}
H
(
f
)
(
x
)
{\displaystyle H(f)(x)}
x 取得局部最小值,如果是負定矩陣,則函數在x 取得局部最大值。在這類情況下,關於函數f 的條件最佳化問題可以轉變為關於海森矩陣的二次規劃 問題[ 74]
矩陣在多元函數微積分中的另一個應用是雅可比矩陣 。函數
f
:
R
n
→
R
m
{\displaystyle f:\mathbf {R} ^{n}\rightarrow \mathbf {R} ^{m}}
x 上的一階偏導數存在時,可以定義它在這點上的雅可比矩陣[ 75]
J
f
(
x
)
=
[
∂
f
i
∂
x
j
(
x
)
]
1
≤
i
≤
m
,
1
≤
j
≤
n
{\displaystyle J_{f}(x)=\left[{\frac {\partial f_{i}}{\partial x_{j}}}(x)\right]_{1\leq i\leq m,1\leq j\leq n}}
n
>
m
{\displaystyle n>m}
J
f
(
x
)
{\displaystyle J_{f}(x)}
m
{\displaystyle m}
反函數定理 ,可以找到函數
f
{\displaystyle f}
x 附近的一個局部的反函數[ 76] 偏微分方程式 理論中,二階擬線性偏微分方程式可以根據最高次偏導項系數構成的矩陣的正定性分類。假設有一個二階擬線性偏微分方程式:
(
E
)
∑
1
⩽
i
,
j
⩽
n
a
i
j
∂
2
f
∂
x
i
∂
x
j
+
∑
i
=
1
n
b
i
∂
f
∂
x
i
+
c
f
=
g
{\displaystyle (\mathbf {E} )\qquad \qquad \sum _{1\leqslant i,j\leqslant n}a_{ij}{\frac {\partial ^{2}f}{\partial x_{i}\,\partial x_{j}}}+\sum _{i=1}^{n}b_{i}{\frac {\partial f}{\partial x_{i}}}+cf=g\qquad }
a
i
j
=
a
j
i
{\displaystyle a_{ij}=a_{ji}}
記矩陣
A
=
[
a
i
j
]
1
⩽
i
,
j
⩽
n
{\displaystyle \mathbf {A} =\left[a_{ij}\right]_{1\leqslant i,j\leqslant n}}
A
{\displaystyle \mathbf {A} }
(
E
)
{\displaystyle (\mathbf {E} )}
A
{\displaystyle \mathbf {A} }
(
E
)
{\displaystyle (\mathbf {E} )}
A
{\displaystyle \mathbf {A} }
n
−
1
{\displaystyle n-1}
(
E
)
{\displaystyle (\mathbf {E} )}
(
E
)
{\displaystyle (\mathbf {E} )}
[ 77]
用數值方法解偏微分方程式時更需要用到矩陣。一個重要的方法是有限元方法 ,在求解各種物理中遇到的偏微分方程式時廣泛使用。有限元方法的基本思想是用一系列「簡單」函數的線性組合來「逼近」偏微分方程式的精確解。這些「簡單」函數通常是指將求解區域分割成一定數量的「小塊」後,僅在某一「小塊」上非零的分段線性函數。選定了網格和「簡單」函數後,可以求解關於剛度矩陣 的方程式得到近似解。有限元理論中證明了在滿足一定的條件下,近似解將隨着網格趨於精細而弱收斂到精確解[ 78] [ 79]
機率論中常用到隨機矩陣 ,即列向量是機率向量 (即所有的元素都在0和1之間,並且加起來等於1的向量)的矩陣。隨機矩陣可用來定義有限機率空間中的馬可夫鏈 。設隨機變量
X
n
{\displaystyle X_{n}}
t
=
n
{\displaystyle t=n}
S
=
{
s
1
,
s
2
,
⋯
,
s
m
}
{\displaystyle S=\left\{s_{1},s_{2},\cdots ,s_{m}\right\}}
M
n
n
+
1
{\displaystyle M_{n}^{n+1}}
X
n
{\displaystyle X_{n}}
X
n
+
1
{\displaystyle X_{n+1}}
[ 80]
M
n
n
+
1
{\displaystyle M_{n}^{n+1}}
i
{\displaystyle i}
j
{\displaystyle j}
X
n
=
s
j
{\displaystyle X_{n}=s_{j}}
X
n
+
1
=
s
i
{\displaystyle X_{n+1}=s_{i}}
M
n
n
+
1
{\displaystyle M_{n}^{n+1}}
j
{\displaystyle j}
X
n
=
s
j
{\displaystyle X_{n}=s_{j}}
X
n
+
1
{\displaystyle X_{n+1}}
M
n
n
+
1
{\displaystyle M_{n}^{n+1}}
t
=
n
{\displaystyle t=n}
吸引態 可以通過計算轉移矩陣的特徵向量得到[ 81]
統計學中也會用到各種不同的矩陣。敘述統計學 中常常需要用矩陣的形式來描述數據樣本,顯得更為緊湊。幾個隨機變量的協方差矩陣 表示它們之間的協方差 關係,在某種程度上表示了它們相互間的關聯程度(但不絕對)[ 82]
統計學中用到矩陣的另一個地方是線性迴歸 中的最小平方法 分析。當觀測到隨機樣本
(
Y
i
,
X
i
1
,
…
,
X
i
p
)
,
i
=
1
,
…
,
n
{\displaystyle (Y_{i},X_{i1},\ldots ,X_{ip}),\,i=1,\ldots ,n}
Y
i
=
β
0
+
β
1
X
i
1
+
β
2
X
i
2
+
…
+
β
p
X
i
p
+
ε
i
,
i
=
1
,
…
,
n
{\displaystyle Y_{i}=\beta _{0}+\beta _{1}X_{i1}+\beta _{2}X_{i2}+\ldots +\beta _{p}X_{ip}+\varepsilon _{i},\qquad i=1,\ldots ,n}
即將變數
Y
{\displaystyle \mathbf {Y} }
X
{\displaystyle \mathbf {X} }
奇異值分解 來分析[ 83]
另一種隨機矩陣(random matrix )是指每個元素都是隨機變量的矩陣,這些隨機變量可以都遵循同一個分佈,或各自遵循不同的分佈。一個常見的例子是全部元素都是相互獨立的標準正態分佈 隨機變量的隨機矩陣。這種隨機矩陣在數論 和物理 中也有應用[ 84] [ 85]
線性轉換及其所對應的對稱 ,在現代物理學中有着重要的角色。例如,在量子場論 中,基本粒子 是由狹義相對論的勞侖茲群 所表示,具體來說,即它們在旋量群 下的表現。內含鮑利矩陣 及更通用的狄拉克矩陣 的具體表示,在費米子 的物理描述中,是一項不可或缺的構成部分,而費米子的表現可以用旋量 來表述[ 86] 夸克 時,需要用到一種內含特殊么正群 SU(3)的群論表示;物理學家在計算時會用一種更簡便的矩陣表示,叫蓋爾曼矩陣 ,這種矩陣也被用作SU(3)規範群 ,而強核力的現代描述──量子色動力學 的基礎正是SU(3)。還有卡比博-小林-益川矩陣 (CKM矩陣):在弱相互作用 中重要的基本夸克態,與指定粒子間不同質素 的夸克態不一樣,但兩者卻是成線性關係,而CKM矩陣所表達的就是這一點[ 87]
1925年海森堡提出第一個量子力學 模型時,使用了無限維矩陣來表示理論中作用在量子態上的算子[ 88] 矩陣力學 中也能見到。例如密度矩陣 就是用來刻畫量子系統中「純」量子態 的線性組合表示的「混合」量子態[ 89]
另一種矩陣是用來描述構成實驗粒子物理基石的散射實驗的重要工具。當粒子在加速器 中發生碰撞,原本沒有相互作用的粒子在高速運動中進入其它粒子的作用區,動量改變,形成一系列新的粒子。這種碰撞可以解釋為結果粒子狀態和入射粒子狀態線性組合的純量積。其中的線性組合可以表達為一個矩陣,稱為S矩陣 ,其中記錄了所有可能的粒子間相互作用[ 90]
矩陣在物理學中的另一類泛應用是描述線性耦合調和系統。這類系統的運動方程式 可以用矩陣的形式來表示,即用一個質素矩陣乘以一個廣義速度來給出運動項,用力矩陣乘以位移向量來刻畫相互作用。求系統的解的最佳方法是將矩陣的特徵向量求出(通過對角化 等方式),稱為系統的簡正模式 。這種求解方式在研究分子內部動力學模式時十分重要:系統內部由化學鍵結合的原子的振動可以表示成簡正振動模式的疊加[ 91] [ 92]
在幾何光學 裏,可以找到很多需要用到矩陣的地方。幾何光學是一種忽略了光波波動性 的近似理論,這理論的模型將光線視為幾何射線 。採用近軸近似 ,假若光線與光軸 之間的夾角很小,則透鏡 或反射 元件對於光線的作用,可以表達為2×2矩陣與向量的乘積。這向量的兩個分量是光線的幾何性質(光線的斜率 、光線跟光軸之間在主平面 光線傳輸矩陣 ,內中元素編碼了光學元件的性質。對於折射,這矩陣又細分為兩種:「折射矩陣」與「平移矩陣」。折射矩陣描述光線遇到透鏡的折射行為。平移矩陣描述光線從一個主平面傳播到另一個主平面的平移行為。
由一系列透鏡或反射元件組成的光學系統,可以很簡單地以對應的矩陣組合來描述其光線傳播路徑。[ 93]
Shen, Crossley & Lun 1999 The Collected Mathematical Papers of James Joseph Sylvester: 1837–1853, Paper 37 (頁面存檔備份 ,存於互聯網檔案館 ), p. 247 Cayley 1889 , vol. II, p. 475–496 Dieudonné, ed. 1978 , Vol. 1, Ch. III, p. 96 Brown 1991 , Definition I.2.1 (addition), Definition I.2.4 (scalar multiplication), and Definition I.2.33 (transpose)
Brown 1991 , Theorem I.2.6 Brown 1991 , Definition I.2.20 Horn & Johnson 1985 , Ch. 4 and 5 Brown 1991 , I.2.21 and 22 Greub 1975 , Section III.2 Brown 1991 , Definition II.3.3 Greub 1975 , Section III.1 Brown 1991 , Theorem II.3.22 Brown 1991 , Definition I.5.13 Brown 1991 , Definition I.2.28 這個結論容易從矩陣乘法的定義獲得:
tr
(
A
B
)
=
∑
i
=
1
m
∑
j
=
1
n
A
i
j
B
j
i
=
tr
(
B
A
)
{\displaystyle \scriptstyle \operatorname {tr} ({\mathsf {AB}})=\sum _{i=1}^{m}\sum _{j=1}^{n}A_{ij}B_{ji}=\operatorname {tr} ({\mathsf {BA}})}
Brown 1991 , Definition III.2.1 Mirsky 1990 , Theorem 1.4.1 Brown 1991 , Theorem III.2.12 Brown 1991 , Corollary III.2.16 Brown 1991 , Theorem III.3.18 Brown 1991 , Definition III.4.1 Steven A. Leduc [[#CITEREFSteven A. Leduc|]], 第293頁
Brown 1991 , Definition III.4.9 Brown 1991 , Corollary III.4.10 Horn & Johnson 1985 , Theorem 2.5.6 Horn & Johnson 1985 , Chapter 7 Horn & Johnson 1985 , Theorem 7.2.1 Golub & Van Loan 1996 , Algorithm 1.3.1 Golub & Van Loan 1996 , Chapters 9 and 10, esp. section 10.2 Golub & Van Loan 1996 , Chapter 2.3 Press, Flannery & Teukolsky 1992 Stoer & Bulirsch 2002 , Section 4.1 Horn & Johnson 1985 , Theorem 2.5.4 Horn & Johnson 1985 , Ch. 3.1, 3.2 Arnold & Cooke 1992 , Sections 14.5, 7, 8 Lang 2002 , XVII.1, p. 643 Lang 2002 , Proposition XIII.4.16 Greub 1975 , Section III.3 Greub 1975 , Section III.3.13 Artin 1991 , Theorem 4.5.13 Rowen 2008 , Example 19.2, p. 198 Fudenberg & Tirole 1983 , Section 1.1.1 Manning 1999 , Section 15.3.4 Stinson 2005 , Ch. 1.1.5 and 1.2.4 Association for Computing Machinery 1979 , Ch. 7 Godsil & Royle 2004 , Ch. 8.1 Latouche & Ramaswami 1999 Mehata & Srinivasan 1978 , Ch. 2.8 Krzanowski 1988 , Ch. 2.2., p. 60 Zabrodin, Brezin & Kazakov et al. 2006
Itzykson & Zuber 1980 , Ch. 2
見Burgess & Moore 2007 , section 1.6.3. (SU(3)), section 2.4.3.2. (Kobayashi-Maskawa matrix) Bohm 2001 , sections II.4 and II.8 Riley, Hobson & Bence 1997 , 7.17
Arnold, Vladimir I.; Cooke, Roger, Ordinary differential equations, Berlin, DE; New York, NY: Springer-Verlag, 1992, ISBN 978-3-540-54813-3 Artin, Michael, Algebra, Prentice Hall, 1991, ISBN 978-0-89871-510-1 Association for Computing Machinery, Computer Graphics, Tata McGraw–Hill, 1979, ISBN 978-0-07-059376-3 Baker, Andrew J., Matrix Groups: An Introduction to Lie Group Theory, Berlin, DE; New York, NY: Springer-Verlag, 2003, ISBN 978-1-85233-470-3 Bau III, David; Trefethen, Lloyd N., Numerical linear algebra, Philadelphia, PA: Society for Industrial and Applied Mathematics, 1997, ISBN 978-0-89871-361-9 Bretscher, Otto, Linear Algebra with Applications 3rd, Prentice Hall, 2005 王萼芳, 高等代数教程 第1版, 清華大學出版社, 1997, ISBN 9787302024521 Bronson, Richard, Schaum's outline of theory and problems of matrix operations, New York: McGraw–Hill, 1989, ISBN 978-0-07-007978-6 Brown, William A., Matrices and vector spaces, New York, NY: M. Dekker, 1991, ISBN 978-0-8247-8419-5 Coburn, Nathaniel, Vector and tensor analysis, New York, NY: Macmillan, 1955, OCLC 1029828 Conrey, J. Brian, Ranks of elliptic curves and random matrix theory, Cambridge University Press , 2007, ISBN 978-0-521-69964-8 Fudenberg, Drew; Tirole, Jean, Game Theory, MIT Press, 1983 Gilbarg, David; Trudinger, Neil S., Elliptic partial differential equations of second order 2nd, Berlin, DE; New York, NY: Springer-Verlag, 2001, ISBN 978-3-540-41160-4 Godsil, Chris; Royle, Gordon, Algebraic Graph Theory, Graduate Texts in Mathematics 207 , Berlin, DE; New York, NY: Springer-Verlag, 2004, ISBN 978-0-387-95220-8 Golub, Gene H.; Van Loan, Charles F., Matrix Computations 3rd, Johns Hopkins, 1996, ISBN 978-0-8018-5414-9 Greub, Werner Hildbert, Linear algebra, Graduate Texts in Mathematics, Berlin, DE; New York, NY: Springer-Verlag, 1975, ISBN 978-0-387-90110-7 Guenther, Robert D., Modern Optics, John Wiley, 1990, ISBN 0-471-60538-7 Halmos, Paul Richard, A Hilbert space problem book, Graduate Texts in Mathematics 19 2nd, Berlin, DE; New York, NY: Springer-Verlag, 1982, ISBN 978-0-387-90685-0MR 0675952 Horn, Roger A.; Johnson, Charles R., Matrix Analysis, Cambridge University Press, 1985, ISBN 978-0-521-38632-6 Householder, Alston S., The theory of matrices in numerical analysis, New York, NY: Dover Publications, 1975, MR 0378371 Krzanowski, Wojtek J., Principles of multivariate analysis, Oxford Statistical Science Series 3 , The Clarendon Press Oxford University Press, 1988, ISBN 978-0-19-852211-9MR 0969370 Itõ, Kiyosi (編), Encyclopedic dictionary of mathematics. Vol. I-IV 2nd, MIT Press, 1987, ISBN 978-0-262-09026-1MR 0901762 Ash, Robert B., A Course In Algebraic Number Theory (PDF) , Dept. of Mathematics, University of Illinois, [2012-04-15 ] , (原始內容存檔 (PDF) 於2017-05-18) Lang, Serge, Analysis II, Addison-Wesley, 1969 Lang, Serge, Calculus of several variables 3rd, Berlin, DE; New York, NY: Springer-Verlag, 1987a, ISBN 978-0-387-96405-8 Lang, Serge, Linear algebra, Berlin, DE; New York, NY: Springer-Verlag, 1987b, ISBN 978-0-387-96412-6 Latouche, Guy; Ramaswami, Vaidyanathan, Introduction to matrix analytic methods in stochastic modeling 1st, Philadelphia, PA: Society for Industrial and Applied Mathematics, 1999, ISBN 978-0-89871-425-8 Manning, Christopher D.; Schütze, Hinrich, Foundations of statistical natural language processing, MIT Press, 1999, ISBN 978-0-262-13360-9 Mehata, K. M.; Srinivasan, S. K., Stochastic processes, New York, NY: McGraw–Hill, 1978, ISBN 978-0-07-096612-3 Mirsky, Leonid, An Introduction to Linear Algebra , Courier Dover Publications, 1990, ISBN 978-0-486-66434-7 Nocedal, Jorge; Wright, Stephen J., Numerical Optimization 2nd, Berlin, DE; New York, NY: Springer-Verlag: 449, 2006, ISBN 978-0-387-30303-1 Bohm, Arno, Quantum Mechanics: Foundations and Applications, Springer, 2001, ISBN 0-387-95330-2 Burgess, Cliff; Moore, Guy, The Standard Model. A Primer, Cambridge University Press, 2007, ISBN 0-521-86036-9 Guenther, Robert D., Modern Optics, John Wiley, 1990, ISBN 0-471-60538-7 Itzykson, Claude; Zuber, Jean-Bernard, Quantum Field Theory, McGraw–Hill, 1980, ISBN 0-07-032071-3 Riley, Kenneth F.; Hobson, Michael P.; Bence, Stephen J., Mathematical methods for physics and engineering, Cambridge University Press, 1997, ISBN 0-521-55506-X Schiff, Leonard I., Quantum Mechanics 3rd, McGraw–Hill, 1968 Weinberg, Steven, The Quantum Theory of Fields. Volume I: Foundations, Cambridge University Press, 1995, ISBN 0-521-55001-7 Wherrett, Brian S., Group Theory for Atoms, Molecules and Solids, Prentice–Hall International, 1987, ISBN 0-13-365461-3 Zabrodin, Anton; Brezin, Édouard; Kazakov, Vladimir; Serban, Didina; Wiegmann, Paul, Applications of Random Matrices in Physics (NATO Science Series II: Mathematics, Physics and Chemistry), Berlin, DE; New York, NY: Springer-Verlag, 2006, ISBN 978-1-4020-4530-1 林志興; 楊忠鵬, 与给定矩阵A的可交换子环C(A)的一些探讨, 莆田學院學報,2010年, 17(2), 2010 Oualline, Steve, Practical C++ programming, O'Reilly , 2003, ISBN 978-0-596-00419-4 Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T., LU Decomposition and Its Applications, Numerical Recipes in FORTRAN: The Art of Scientific Computing (PDF) 2nd, Cambridge University Press: 34–42, 1992, (原始內容 (PDF) 存檔於2009-09-06) Punnen, Abraham P.; Gutin, Gregory, The traveling salesman problem and its variations, Boston, MA: Kluwer Academic Publishers, 2002, ISBN 978-1-4020-0664-7 Reichl, Linda E., The transition to chaos: conservative classical systems and quantum manifestations, Berlin, DE; New York, NY: Springer-Verlag, 2004, ISBN 978-0-387-98788-0 Rowen, Louis Halle, Graduate Algebra: noncommutative view, Providence, RI: American Mathematical Society , 2008, ISBN 978-0-8218-4153-2 Šolin, Pavel, Partial Differential Equations and the Finite Element Method, Wiley-Interscience, 2005, ISBN 978-0-471-76409-0 Stinson, Douglas R., Cryptography, Discrete Mathematics and its Applications, Chapman & Hall/CRC, 2005, ISBN 978-1-58488-508-5 Stoer, Josef; Bulirsch, Roland, Introduction to Numerical Analysis 3rd, Berlin, DE; New York, NY: Springer-Verlag, 2002, ISBN 978-0-387-95452-3 Ward, J. P., Quaternions and Cayley numbers, Mathematics and its Applications 403 , Dordrecht, NL: Kluwer Academic Publishers Group, 1997, ISBN 978-0-7923-4513-8MR 1458894 (中文) 居余馬; 林翠琴, 线性代数, 清華大學出版社, 2002, ISBN 978-7-302-06507-4 (中文) 克萊因, 莫里斯; 著,張理京、張錦炎、江澤涵 譯, 《古今数学思想》第三卷, 上海科學技術出版社, 2002, ISBN 7-5323-6172-1 Wolfram, Stephen, The Mathematica Book 5th, Champaign, IL: Wolfram Media, 2003, ISBN 978-1-57955-022-6 Thankappan, V. K., Quantum Mechanics 2nd, New Age International, 1993, ISBN 9788122405262 Faliva, Mario; Zoia, Maria Grazia, Dynamic Model Analysis: Advanced Matrix Methods and Unit-Root Econometrics Representation Theorems 2nd, Berlin, DE; New York, NY: Springer-Verlag: 218, 2008, ISBN 9783540859956 伊澤爾萊斯, 劉曉艷,劉學深譯, 微分方程数值分析基础教程, 清華大學出版社, 2005, ISBN 9787302106524 董可榮, 矩阵理论的历史研究, 《山東大學》, 2007 Bôcher, Maxime, Introduction to higher algebra, New York, NY: Dover Publications, 2004, ISBN 978-0-486-49570-5 Cayley, Arthur, The collected mathematical papers of Arthur Cayley , I (1841–1853), Cambridge University Press: 123–126, 1889 Dieudonné, Jean (編), Abrégé d'histoire des mathématiques 1700-1900, Paris, FR: Hermann, 1978Hawkins, Thomas, Cauchy and the spectral theory of matrices, Historia Mathematica, 1975, 2 : 1–29, ISSN 0315-0860 MR 0469635 doi:10.1016/0315-0860(75)90032-4 Knobloch, Eberhard, From Gauss to Weierstrass: determinant theory and its historical evaluations, The intersection of history and mathematics, Science Networks Historical Studies 15 , Basel, Boston, Berlin: Birkhäuser: 51–66, 1994, MR 1308079 Kronecker, Leopold, Hensel, Kurt , 編, Leopold Kronecker's Werke , Teubner, 1897 Mehra, Jagdish; Rechenberg, Helmut, The Historical Development of Quantum Theory 1st, Berlin, DE; New York, NY: Springer-Verlag, 1987, ISBN 978-0-387-96284-9 Shen, Kangshen; Crossley, John N.; Lun, Anthony Wah-Cheung, Nine Chapters of the Mathematical Art, Companion and Commentary 2nd, Oxford University Press, 1999, ISBN 978-0-19-853936-0 Weierstrass, Karl, Collected works 3 , 1915 [2012-05-06 ] , (原始內容存檔 於2008-10-11)
百科全書 歷史 線上書籍 Kaw, Autar K., Introduction to Matrix Algebra , [2015-01-10 ] , ISBN 978-0-615-25126-4存檔 於2008-08-08) The Matrix Cookbook (PDF) , [2014-03-24 ] , (原始內容存檔 (PDF) 於2013-12-12)Brookes, Mike, The Matrix Reference Manual , London: Imperial College , 2005 [2008-12-10 ] , (原始內容存檔 於2021-03-22) 線上矩陣計數機 Matrix Calculator (DotNumerics) , [2015-01-10 ] , (原始內容 存檔於2014-09-04)Xiao, Gang, Matrix calculator , [2008-12-10 ] , (原始內容存檔 於2020-06-12) Online matrix calculator , [2008-12-10 ] , (原始內容 存檔於2008-12-12)Online matrix calculator (ZK framework) , [2009-11-26 ] , (原始內容 存檔於2013-05-12)Oehlert, Gary W.; Bingham, Christopher, MacAnova , University of Minnesota , School of Statistics, [2008-12-10 ] , (原始內容存檔 於2021-03-22) , a freeware package for matrix algebra and statisticsOnline matrix calculator , [2009-12-14 ] , (原始內容存檔 於2021-04-27)Operation with matrices in R (determinant, track, inverse, adjoint, transpose) (頁面存檔備份 ,存於互聯網檔案館 ) 




























![{\displaystyle \mathbf {A} _{[i,j]}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6a8b9bccc1ff7fa48155b222898cc3fb9c43765d)

![{\displaystyle \mathbf {A} =[\mathrm {a} _{ij}]_{m\times n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/c5de84bb1cf264ef179edc39abc26d03dc3533e4)
![{\displaystyle \mathbf {A} =[\mathrm {a} _{i,\,j}]_{m\times n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1f0302ef6b6aa24107b929177c44604f99c2a9d4)



![{\displaystyle \mathbf {A} =[T(i,\,j)]_{m\times n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/59b18cede47061b8d3ab925a8ced2a6fdc4008ed)


![{\displaystyle \mathbf {A} =[i+j]_{m\times n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/52f2046f9a9e7aa6cb357b2d1dd4d13ba674bf9d)





![{\displaystyle \mathbf {B} =\left[i+2j\right]_{2\times 3}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/983a530d365d0e9b8cdbfb1eae041f89d403c6ac)


![{\displaystyle \mathbf {B} =\left[i+2j+3\right]_{2\times 3}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0f2a9de3c58ca7990e946b699273dbbccec787e5)
































![{\displaystyle [\mathbf {AB} ]_{i,j}=A_{i,1}B_{1,j}+A_{i,2}B_{2,j}+\cdots +A_{i,n}B_{n,j}=\sum _{r=1}^{n}A_{i,r}B_{r,j}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/db581eb370e44283170093b08a2ae8407bc38314)













































































































































![{\displaystyle H(f)(x)=\left[{\frac {\partial ^{2}f}{\partial x_{i}\,\partial x_{j}}}(x)\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b933754bfe181046375b707808338537bbb459a5)










![{\displaystyle J_{f}(x)=\left[{\frac {\partial f_{i}}{\partial x_{j}}}(x)\right]_{1\leq i\leq m,1\leq j\leq n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/50fbeb6d77601ce7cde35e0d842e6af992c9ccf5)




![{\displaystyle \mathbf {A} =\left[a_{ij}\right]_{1\leqslant i,j\leqslant n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3b3772f4e0a0e32adcf80e2c5c94496c1f60af43)
























