矩陣

數學上，一個${\displaystyle m\times n}$的矩陣（英語：matrix）是一個有${\displaystyle m}$列（row）${\displaystyle n}$行（column）元素的矩形陣列。矩陣裏的元素可以是數字或符號甚至是函數。

${\displaystyle {\begin{bmatrix}a_{11}&a_{12}&a_{13}&\dots &a_{1j}&\dots &a_{1n}\\a_{21}&a_{22}&a_{23}&\dots &a_{2j}&\dots &a_{2n}\\a_{31}&a_{32}&a_{33}&\dots &a_{3j}&\dots &a_{3n}\\\vdots &\vdots &\vdots &\ddots &\vdots &\ddots &\vdots \\a_{i1}&a_{i2}&a_{i3}&\dots &a_{ij}&\dots &a_{in}\\\vdots &\vdots &\vdots &\ddots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&a_{m3}&\dots &a_{mj}&\dots &a_{mn}\end{bmatrix}}}$

線性代數
${\displaystyle \mathbf {A} ={\begin{bmatrix}1&2\\3&4\end{bmatrix}}}$
向量 · 向量空間 · 基底  · 行列式  · 矩陣
向量 純量 · 向量 · 向量空間 · 向量投影 · 外積（叉積 · 七維叉積） · 內積（點積） · 二重向量 矩陣與行列式 矩陣 · 行列式 · 線性方程組 · 秩 · 核 · 跡 · 單位矩陣 · 初等矩陣 · 方塊矩陣 · 分塊矩陣 · 三角矩陣 · 非奇異方陣 · 轉置矩陣 · 逆矩陣 · 對角矩陣 · 可對角化矩陣 · 對稱矩陣 · 反對稱矩陣 · 正交矩陣 · 么正矩陣 · 埃爾米特矩陣 · 反埃爾米特矩陣 · 正規矩陣 · 伴隨矩陣 · 餘因子矩陣 · 共軛轉置 · 正定矩陣 · 冪零矩陣 · 矩陣分解 （LU分解 · 奇異值分解 · QR分解 · 極分解 · 特徵分解） · 子式和餘子式 · 拉普拉斯展開 · 克羅內克積 線性空間與線性轉換 線性空間 · 線性轉換 · 線性子空間 · 線性生成空間 · 基 · 線性對映 · 線性投影 · 線性無關 · 線性組合 · 線性泛函 · 行空間與列空間 · 對偶空間 · 正交 · 特徵向量 · 最小平方法 · 格拉姆-施密特正交化
閱 論 編

「m-by-n matrix」的各地常用名稱
中國大陸	${\displaystyle m}$行${\displaystyle n}$列矩陣
臺灣	${\displaystyle m}$列${\displaystyle n}$行矩陣

「橫排（row）」的各地常用名稱
中國大陸	行
臺灣	列

「縱排（column）」的各地常用名稱
中國大陸	列
臺灣	行

大小相同（行數列數都相同）的矩陣之間可以相互加減，具體是對每個位置上的元素做加減法。矩陣乘法則較為複雜。兩個矩陣可以相乘，若且唯若第一個矩陣的行數等於第二個矩陣的列數。矩陣乘法滿足結合律和分配律，但不滿足交換律。

矩陣的一個重要用途是解線性方程組。線性方程組中未知量的系數可以排成一個矩陣，加上常數項，則稱為增廣矩陣。另一個重要用途是表示線性轉換，即是諸如${\displaystyle f(x)=4x}$之類的線性函數的推廣。設定基底後，某個向量${\displaystyle \mathrm {v} }$可以表示為${\displaystyle m\times 1}$的矩陣，而線性轉換${\displaystyle f}$可以表示為行數為${\displaystyle m}$的矩陣${\displaystyle A}$，使得經過轉換後得到的向量${\displaystyle f(\mathrm {v} )}$可以表示成${\displaystyle A\mathrm {v} }$的形式。矩陣的特徵值和特徵向量可以揭示線性轉換的深層特性。

矩陣是高等代數學中的常見工具，也常見於統計分析等應用數學學科中。在物理學中，矩陣在力學、電路學、光學和量子物理等領域中都有應用；電腦科學中，三維動畫製作也需要用到矩陣。矩陣的運算是數值分析領域的重要問題。將矩陣分解為簡單矩陣的組合可以在理論和實際應用上簡化矩陣的運算。對一些應用廣泛而形式特殊的矩陣，例如稀疏矩陣和准對角矩陣，有特定的快速運算演算法。關於矩陣相關理論的發展和應用，請參考矩陣理論。在天體物理、量子力學等領域，也會出現無窮維的矩陣，是矩陣的一種推廣。

詞源

中文中矩陣的概念最早見於1922年。1922年，北京師範大學附屬中學數學老師程廷熙在一篇介紹文章中將矩陣譯為「縱橫陣」。1925年，在科學名詞審查會算學名詞審查組刊登於《科學》第十卷第四期的審定名詞表中，矩陣被翻譯為「矩陣式」，方塊矩陣翻譯為「方陣式」，而各類矩陣如「正交矩陣」、「伴隨矩陣」中的「矩陣」則被翻譯為「方陣」。1935年，中國數學會審查後，中華民國教育部審定的《數學名詞》（並「通令全國各院校一律遵用，以昭劃一」）中，「矩陣」作為譯名首次出現。1938年，曹惠群在接受科學名詞審查會委託就數學名詞加以校訂的《算學名詞彙編》中，認為應當的譯名是「長方陣」。1949年中華人民共和國成立後編訂的《數學名詞》中，則將譯名定為「（矩）陣」。1993年，中國自然科學名詞審定委員會公佈的《數學名詞》中，「矩陣」被定為正式譯名，並沿用至今^[1]。

發展

作為解決線性方程式的工具，矩陣也有不短的歷史。成書最遲在東漢前期的《九章算術》中，已經出現過以矩陣形式表示線性方程組系數以解方程式的圖例，可視為矩陣的雛形^[2]。矩陣正式作為數學中的研究物件出現，則是在行列式的研究發展起來後。邏輯上，矩陣的概念先於行列式，但在歷史上則恰好相反。日本數學家關孝和（1683年）與微積分的發現者之一戈特弗里德·威廉·萊布尼茨（1693年）近乎同時獨立建立了行列式論。其後行列式作為解線性方程組的工具逐步發展。1750年，加布里爾·克拉默發現了克拉瑪公式^[3]。

阿瑟·凱萊被認為是矩陣論的奠基人

進入十九世紀後，行列式的研究進一步發展，矩陣的概念也應運而生。奧古斯丁·路易·柯西是最早將行列式排成方陣並將其元素用雙重下標表示的數學家。他還在1829年就在行列式的框架中證明了實對稱矩陣特徵根為實數的結論^[4]。其後，詹姆斯·約瑟夫·西爾維斯特注意到，在作為行列式的計算形式以外，將數以行和列的形式作出的矩形排列本身也是值得研究的。在他希望參照數的矩形陣列而又不能用行列式來形容的時候，就用「matrix」一詞來形容^[3]。而在此之前，數學家已經開始將增廣矩陣作為獨立的物件參照了。西爾維斯特使用「matrix」一詞是因為他希望討論行列式的子式，即將矩陣的某幾行和某幾列的共同元素取出來排成的矩陣的行列式，所以實際上「matrix」被他看做是生成各種子式的「母體」：

我在先前的文章中將矩形排布的序列稱為「Matrix」，蓋因從中可以產生出各種不同的行列式，就如由同一個母體的子宮中孕育出來一樣。^[5]

阿瑟·凱萊被公認為矩陣論的奠基人^[3]。他開始將矩陣作為獨立的數學物件研究時，許多與矩陣有關的性質已經在行列式的研究中被發現，這也使得凱萊認為矩陣的引進是十分自然的。他說：「我決然不是通過四元數而獲得矩陣概念的；它或是直接從行列式的概念而來，或是作為一個表達線性方程組的方便方法而來的。^[3]」他從1858年開始，發表了《矩陣論的研究報告》等一系列關於矩陣的專門論文^[6][7]，研究了矩陣的運算律、矩陣的逆以及轉置和特徵多項式方程式。凱萊還提出了凱萊-哈密爾頓定理，並驗證了3×3矩陣的情況，又說進一步的證明是不必要的。哈密爾頓證明了4×4矩陣的情況，而一般情況下的證明是弗比尼斯於1898年給出的^[3]。

此後更多數學家開始對矩陣進行研究。埃爾米特證明了如果矩陣等於其複共軛轉置，則特徵根為實數。這種矩陣後來被稱為埃爾米特矩陣^[3]。弗比尼斯對矩陣的特徵方程式、特徵根、矩陣的秩、正交矩陣、矩陣方程式等方面做了大量工作。1878年，在引進了不變因子、初等因子等概念的同時，弗比尼斯給出了正交矩陣、相似矩陣和合同矩陣的概念。同年，他探討了矩陣的最小多項式（最小方程式）問題。1894年的論文中，他討論了矩陣理論和四元數理論的關係。1896年，他給出了凱萊-哈密爾頓定理的完整證明^[1]。矩陣理論在19世紀沿着兩個方向發展，分別是作為抽象代數結構和作為代數工具描述幾何空間的線性轉換。矩陣理論為群論和不變數理論的發展。

無限維矩陣的研究始於1884年。龐加萊在兩篇不嚴謹地使用了無限維矩陣和行列式理論的文章後開始了對這一方面的專門研究^[1]。1906年，希爾伯特引入無限二次型（相當於無限維矩陣）對積分方程式進行研究，極大地促進了無限維矩陣的研究。在此基礎上，施密茨、赫林格和特普利茨發展出算子理論，而無限維矩陣成為了研究函數空間算子的有力工具^[1]。

正式定義

矩陣的定義 — ${\displaystyle S}$ 是一個集合，那函數 ${\displaystyle \mathbf {A} :\{1,\,2,\,\ldots ,\,m\}\times \{1,\,2,\,\ldots ,\,n\}\to S}$ 就會被稱為定義在 ${\displaystyle S}$ 上的 ${\displaystyle m\times n}$ 矩陣

直觀上就是用兩個數碼去標記一堆數學實體（如數字、函數），實際上是有限序列的一種推廣。

${\displaystyle \mathbf {A} (i,\,j)}$ 被暱稱為矩陣 ${\displaystyle \mathbf {A} }$ 裏的元素，通常簡記為${\displaystyle \mathbf {A} _{i,j}}$、${\displaystyle \mathbf {A} _{ij}}$或${\displaystyle \mathbf {A} _{[i,j]}}$。除此之外也會用小寫字母 ${\displaystyle \mathrm {a} _{ij}}$ 表示元素，來跟矩陣 ${\displaystyle \mathbf {A} }$ 本身做區別。但不知 ${\displaystyle \mathbf {A} }$ 的具體形式卻想強調 ${\displaystyle \mathrm {a} _{ij}}$ 為 ${\displaystyle \mathbf {A} }$ 的元素的話，可以 ${\displaystyle \mathbf {A} =[\mathrm {a} _{ij}]_{m\times n}}$ 或 ${\displaystyle \mathbf {A} =[\mathrm {a} _{i,\,j}]_{m\times n}}$ 表示。

如果表達式 ${\displaystyle f(i,\,j)=T(i,j)}$（嚴格來說是合式公式，其中 ${\displaystyle T}$ 為一個包含變數 ${\displaystyle T(i,\,j)}$ 的項）可以唯一決定一個矩陣 ${\displaystyle \mathbf {A} }$ ，那會將它記成 ${\displaystyle \mathbf {A} =[T(i,\,j)]_{m\times n}}$ 。如：

${\displaystyle \mathbf {A} :\{1,\,2,\,\ldots ,\,m\}\times \{1,\,2,\,\ldots ,\,n\}\to \mathbb {N} }$ 且 ${\displaystyle \mathbf {A} (i,\,j)=i+j}$

就可以表達為 ${\displaystyle \mathbf {A} =[i+j]_{m\times n}}$ 。

根據公理化集合論，可以定義一個函數的集合 ${\displaystyle S^{m\times n}}$ ，它囊括所有定義在 ${\displaystyle S}$ 上的 ${\displaystyle m\times n}$ 矩陣，也就是說：

${\displaystyle S^{m\times n}:=\left\{f\,|\,f:\{1,\,2,\,\ldots ,\,m\}\times \{1,\,2,\,\ldots ,\,n\}\to S\right\}}$

行與列

以下的 ${\displaystyle 3\times 2}$ 矩陣：

${\displaystyle \left\{\left((1,\,1),\,a\right),\,\left((1,\,2),\,b\right),\,\left((2,\,1),\,c\right),\,\left((2,\,2),\,d\right),\,\left((3,\,1),\,e\right),\,\left((3,\,2),\,f\right)\right\}}$

一般會如下排列成為矩形來表示：

${\displaystyle {\begin{bmatrix}a&b\\c&d\\e&f\end{bmatrix}}}$

英文將橫向的元素組統稱為「row」，縱向統稱為「column」；但兩岸對此卻以不同的稱呼；在中國大陸，橫向的元素組稱為「行」，縱向稱為「列」，而在臺灣則相反，橫向稱為「列」，縱向稱為「行」^[8]。

行數是1或列數是1的矩陣又可分別稱為行向量和列向量，在有限維的情況下，向量可用其分量表示成行數或列數是1的矩陣。

範例

${\displaystyle \mathbf {B} =\left[i+2j\right]_{2\times 3}}$是矩陣

${\displaystyle \mathbf {B} ={\begin{bmatrix}3&5&7\\4&6&8\end{bmatrix}}}$

的簡寫。要注意的是，電腦編程中，由於陣列的首項是第0項，故編程者可能會將第1行／列稱為第0行／列，從而對矩陣的寫法產生影響，比如矩陣${\displaystyle \mathbf {B} }$就要覆寫成${\displaystyle \mathbf {B} =\left[i+2j+3\right]_{2\times 3}}$。

矩陣的元素可以是數字、符號或數學表達式。一般為了支援矩陣的運算，矩陣的元素之間應當能做加減法和乘法，所以是某個環裏的元素。最常見的是元素屬於實數體或複數體的矩陣，簡稱為實矩陣和複矩陣。更一般的情況下，矩陣的元素可以是由一個環中的元素排成。給定一個環${\displaystyle \mathbf {R} }$，所有由${\displaystyle \mathbf {R} }$中元素排成的${\displaystyle m\times n}$矩陣的集合寫作${\displaystyle {\mathcal {M}}(m,n,\mathbf {R} )}$或${\displaystyle {\mathcal {M}}_{m\times n}(\mathbf {R} )}$。若${\displaystyle m=n}$，則通常記以${\displaystyle {\mathcal {M}}(m,\mathbf {R} )}$或${\displaystyle {\mathcal {M}}_{m}(\mathbf {R} )}$，稱其為${\displaystyle n}$維矩陣或方陣。

矩陣的基本運算

主條目：矩陣加法、轉置矩陣和初等矩陣

矩陣的最基本運算包括矩陣加（減）法，實數積和轉置運算。被稱為「矩陣加法」、「實數積」和「轉置」的運算不止一種^[9]，其中最基本最常用的定義如下：

運算	定義	例子
加（減）法	${\displaystyle m\times n}$矩陣${\displaystyle \mathbf {A} }$和${\displaystyle \mathbf {B} }$的和（差）：${\displaystyle \mathbf {A} \pm \mathbf {B} }$為一個${\displaystyle m\times n}$矩陣，其中每個元素是${\displaystyle \mathbf {A} }$和${\displaystyle \mathbf {B} }$相應元素的和（差）， ${\displaystyle (\mathbf {A} \pm \mathbf {B} )_{i,j}=\mathbf {A} _{i,j}\pm \mathbf {B} _{i,j}}$， 其中${\displaystyle 1\leq i\leq m,1\leq j\leq n}$	${\displaystyle {\begin{bmatrix}1&3&1\\1&0&0\end{bmatrix}}+{\begin{bmatrix}0&0&5\\7&5&0\end{bmatrix}}={\begin{bmatrix}1+0&3+0&1+5\\1+7&0+5&0+0\end{bmatrix}}={\begin{bmatrix}1&3&6\\8&5&0\end{bmatrix}}}$
實數積	純量${\displaystyle c}$與矩陣${\displaystyle \mathbf {A} }$的實數積：${\displaystyle c\mathbf {A} }$的每個元素是${\displaystyle \mathbf {A} }$的相應元素與${\displaystyle c}$的乘積， ${\displaystyle (c\mathbf {A} )_{i,j}=c\cdot \mathbf {A} _{i,j}}$	${\displaystyle 2\cdot {\begin{bmatrix}1&8&-3\\4&-2&5\end{bmatrix}}={\begin{bmatrix}2\cdot 1&2\cdot 8&2\cdot (-3)\\2\cdot 4&2\cdot (-2)&2\cdot 5\end{bmatrix}}={\begin{bmatrix}2&16&-6\\8&-4&10\end{bmatrix}}}$
轉置	${\displaystyle m\times n}$矩陣${\displaystyle \mathbf {A} }$的轉置是一個${\displaystyle n\times m}$的矩陣，記為${\displaystyle \mathbf {A} ^{\mathrm {T} }}$（有些書中也記為${\displaystyle \mathbf {A} ^{\mathrm {tr} }}$或${\displaystyle ^{\mathrm {t} }\mathbf {A} }$、${\displaystyle \mathbf {A} '}$），其中的第${\displaystyle i}$個列向量是原矩陣${\displaystyle \mathbf {A} }$的第${\displaystyle i}$個行向量；或者說，轉置矩陣${\displaystyle \mathbf {A} ^{\mathrm {T} }}$第${\displaystyle i}$列第${\displaystyle j}$行的元素是原矩陣${\displaystyle \mathbf {A} }$第${\displaystyle j}$列第${\displaystyle i}$行的元素， ${\displaystyle (\mathbf {A} ^{\mathrm {T} })_{i,j}=\mathbf {A} _{j,i}}$	${\displaystyle {\begin{bmatrix}1&2&3\\0&-6&7\end{bmatrix}}^{T}={\begin{bmatrix}1&0\\2&-6\\3&7\end{bmatrix}}}$

矩陣的加法運算滿足交換律：${\displaystyle \mathbf {A} +\mathbf {B} =\mathbf {B} +\mathbf {A} }$^[10]。矩陣的轉置和實數積運算對加法滿足分配律：

${\displaystyle (\mathbf {A} +\mathbf {B} )^{\mathrm {T} }=\mathbf {A} ^{\mathrm {T} }+\mathbf {B} ^{\mathrm {T} }}$

${\displaystyle c(\mathbf {A} +\mathbf {B} )=c\mathbf {A} +c\mathbf {B} }$

矩陣加法和實數積兩種運算使得${\displaystyle {\mathcal {M}}(m,n,\mathbb {R} )}$成為一個${\displaystyle mn}$維的實數線性空間。而轉置和實數積運算滿足類似於結合律的規律：

${\displaystyle c(\mathbf {A} ^{\mathrm {T} })=c(\mathbf {A} )^{\mathrm {T} }}$

矩陣也有類似行列式的初等轉換，即對矩陣的某些行和某些列進行三類操作：交換兩行／列，將一行／列的每個元素都乘以一個固定的量，以及將一行／列的每個元素乘以一個固定的量之後加到另一行／列的相應元素上。這些操作在求其逆矩陣時有用。

矩陣乘法

主條目：矩陣乘法

矩陣A和B相乘得到AB的示意圖

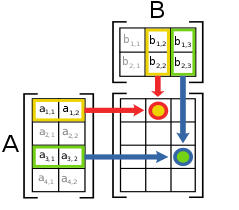
兩個矩陣的乘法僅當第一個矩陣${\displaystyle \mathbf {A} }$的行數(column)和另一個矩陣${\displaystyle \mathbf {B} }$的列數(row)相等時才能定義。如${\displaystyle \mathbf {A} }$是${\displaystyle m\times n}$矩陣和${\displaystyle \mathbf {B} }$是${\displaystyle n\times p}$矩陣，它們的乘積${\displaystyle \mathbf {AB} }$是一個${\displaystyle m\times p}$矩陣，它的一個元素

${\displaystyle [\mathbf {AB} ]_{i,j}=A_{i,1}B_{1,j}+A_{i,2}B_{2,j}+\cdots +A_{i,n}B_{n,j}=\sum _{r=1}^{n}A_{i,r}B_{r,j}}$

其中${\displaystyle 1\leq i\leq m,\ 1\leq j\leq p'}$'^[11]。

例如

${\displaystyle {\begin{bmatrix}1&0&2\\-1&3&1\\\end{bmatrix}}\times {\begin{bmatrix}3&1\\2&1\\1&0\end{bmatrix}}={\begin{bmatrix}(1\times 3+0\times 2+2\times 1)&(1\times 1+0\times 1+2\times 0)\\(-1\times 3+3\times 2+1\times 1)&(-1\times 1+3\times 1+1\times 0)\\\end{bmatrix}}={\begin{bmatrix}5&1\\4&2\\\end{bmatrix}}}$

矩陣的乘法滿足結合律和對矩陣加法的分配律（左分配律和右分配律）：

• 結合律：${\displaystyle (\mathbf {AB} )\mathbf {C} =\mathbf {A} (\mathbf {BC} )}$
• 左分配律：${\displaystyle (\mathbf {A} +\mathbf {B} )\mathbf {C} =\mathbf {AC} +\mathbf {BC} }$
• 右分配律：${\displaystyle \mathbf {C} (\mathbf {A} +\mathbf {B} )=\mathbf {CA} +\mathbf {CB} }$

矩陣的乘法與實數積運算之間也滿足類似結合律的規律；與轉置之間則滿足倒置的分配律。

${\displaystyle c(\mathbf {AB} )=(c\mathbf {A} )\mathbf {B} =\mathbf {A} (c\mathbf {B} )}$

${\displaystyle (\mathbf {AB} )^{\mathrm {T} }=\mathbf {B} ^{\mathrm {T} }\mathbf {A} ^{\mathrm {T} }}$

矩陣乘法不滿足交換律。一般來說，矩陣${\displaystyle \mathbf {A} }$及${\displaystyle \mathbf {B} }$的乘積${\displaystyle \mathbf {AB} }$存在，但${\displaystyle \mathbf {BA} }$不一定存在，即使存在，大多數時候${\displaystyle \mathbf {AB} \neq \mathbf {BA} }$。比如下面的例子：

${\displaystyle {\begin{bmatrix}1&2\\3&4\\\end{bmatrix}}{\begin{bmatrix}0&1\\0&0\\\end{bmatrix}}={\begin{bmatrix}0&1\\0&3\\\end{bmatrix}},\qquad \quad {\begin{bmatrix}0&1\\0&0\\\end{bmatrix}}{\begin{bmatrix}1&2\\3&4\\\end{bmatrix}}={\begin{bmatrix}3&4\\0&0\\\end{bmatrix}}}$。

這一特性使得矩陣代數與常見的一些數體（有理數、實數、複數）以及環（多項式環、整數環）都不同。給定一個${\displaystyle n}$維的方塊矩陣${\displaystyle \mathbf {A} }$，與${\displaystyle \mathbf {A} }$交換的所有方塊矩陣構成一個環，稱為${\displaystyle \mathbf {A} }$的交換子環。這些矩陣也構成${\displaystyle {\mathcal {M}}(n,\mathbb {R} )}$的一個子空間，稱為${\displaystyle \mathbf {A} }$的可交換空間^[12]。與${\displaystyle {\mathcal {M}}(n,\mathbb {R} )}$中所有矩陣交換的矩陣只有形如${\displaystyle \lambda \mathbf {I} _{n},\,\lambda \in \mathbb {R} }$的矩陣（稱為實數積矩陣）。其中的${\displaystyle \mathbf {I} _{n}}$是單位矩陣，也就是主對角線上的元素為1，其它元素為0的矩陣。任意矩陣${\displaystyle \mathbf {M} }$乘以單位矩陣都得到自身：${\displaystyle \mathbf {M} \mathbf {I} _{n}=\mathbf {M} =\mathbf {I} _{n}\mathbf {M} }$。

除了最常見的矩陣乘法定義以外，也有一些較不常見的矩陣乘法，比如阿達馬乘積和克羅內克乘積^[13]。

線性方程組

主條目：線性方程組

矩陣乘法的一個基本應用是線上性方程組上。線性方程組是方程組的一種，它符合以下的形式：

${\displaystyle {\begin{cases}a_{1,1}x_{1}+a_{1,2}x_{2}+\cdots +a_{1,n}x_{n}=b_{1}\\a_{2,1}x_{1}+a_{2,2}x_{2}+\cdots +a_{2,n}x_{n}=b_{2}\\\vdots \quad \quad \quad \vdots \\a_{m,1}x_{1}+a_{m,2}x_{2}+\cdots +a_{m,n}x_{n}=b_{m}\end{cases}}}$

其中的${\displaystyle a_{1,1},\,a_{1,2}}$以及${\displaystyle b_{1},\,b_{2}}$等等是已知的常數，而${\displaystyle x_{1},\,x_{2}}$等等則是要求的未知數。運用矩陣的方式，可以將線性方程組寫成一個向量方程式：

${\displaystyle \mathbf {A} \mathbf {x} =\mathbf {b} }$

其中，${\displaystyle \mathbf {A} }$是由方程組里未知量的系數排成的${\displaystyle m\times n}$矩陣，${\displaystyle \mathbf {x} }$是含有${\displaystyle n}$個元素的列向量，${\displaystyle \mathbf {b} }$是含有${\displaystyle m}$個元素的列向量^[14]。

${\displaystyle \mathbf {A} ={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{m,1}&a_{m,2}&\cdots &a_{m,n}\end{bmatrix}},\quad \mathbf {x} ={\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix}},\quad \mathbf {b} ={\begin{bmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{bmatrix}}}$

這個寫法下，將原來的多個方程式轉化成一個向量方程式，在已知矩陣${\displaystyle \mathbf {A} }$和向量${\displaystyle \mathbf {b} }$的情況下，求未知向量${\displaystyle \mathbf {x} }$。

線性轉換

主條目：線性轉換

矩陣是線性轉換的便利表達法。矩陣乘法的本質在聯絡到線性轉換的時候最能體現，因為矩陣乘法和線性轉換的合成有以下的聯絡： 以${\displaystyle \mathbb {R} ^{n}}$表示所有長度為${\displaystyle n}$的列向量的集合。每個${\displaystyle m\times n}$的矩陣${\displaystyle \mathbf {A} }$都代表了一個從${\displaystyle \mathbb {R} ^{n}}$射到${\displaystyle \mathbb {R} ^{m}}$的線性轉換。反過來，對每個線性轉換${\displaystyle f:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}}$，都存在唯一m×n矩陣${\displaystyle \mathbf {A} _{f}}$使得對所有${\displaystyle \mathbb {R} ^{n}}$中的元素${\displaystyle x}$，${\displaystyle f(x)=A_{f}x}$。這個矩陣${\displaystyle \mathbf {A} _{f}}$第${\displaystyle i}$列第${\displaystyle j}$行上的元素是正則基向量${\displaystyle \mathbf {e} _{j}=(0,\cdots ,0,1,0,\cdots 0)^{T}}$（第j個元素是1，其餘元素是0的向量）在${\displaystyle f}$對映後的向量${\displaystyle f(\mathbf {e} _{j})}$的第${\displaystyle i}$個元素。

也就是說，從${\displaystyle \mathbb {R} ^{n}}$射到${\displaystyle \mathbb {R} ^{m}}$的線性轉換構成的向量空間${\displaystyle {\mathcal {L}}\left(\mathbb {R} ^{n},\mathbb {R} ^{m}\right)}$上存在一個到${\displaystyle {\mathcal {M}}(m,n,\mathbb {R} )}$的一一對映：${\displaystyle f\mapsto A_{f}}$

以下是一些典型的2維實平面上的線性轉換對平面向量（圖形）造成的效果，以及它們對應的2維矩陣。其中每個線性轉換將藍色圖形對映成綠色圖形；平面的原點(0, 0)用黑點表示。

推移， 幅度m=1.25.	水平鏡射轉換	「擠壓」轉換， 壓縮程度r=3/2	伸縮，3/2倍	旋轉，左轉30°
${\displaystyle {\begin{bmatrix}1&1.25\\0&1\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}-1&0\\0&1\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\frac {3}{2}}&0\\0&{\frac {2}{3}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\frac {3}{2}}&0\\0&{\frac {3}{2}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}\cos({\frac {\pi }{6}})&-\sin({\frac {\pi }{6}})\\\sin({\frac {\pi }{6}})&\cos({\frac {\pi }{6}})\end{bmatrix}}}$

設有${\displaystyle k\times m}$的矩陣${\displaystyle \mathbf {B} }$代表線性變換${\displaystyle g:\mathbf {R} ^{m}\rightarrow \mathbf {R} ^{k}}$，則矩陣積${\displaystyle \mathbf {BA} }$代表了綫性變換的複合${\displaystyle g\circ f}$^[15]，因為

${\displaystyle (g\circ f)(x)=g(f(x))=g(\mathbf {Ax} )=\mathbf {B} (\mathbf {Ax} )=(\mathbf {BA} )\mathbf {x} }$

矩陣的秩是指矩陣中線性無關的行／列向量的最大個數^[16]，同時也是矩陣對應的線性轉換的像空間的維度^[17]。秩－零化度定理說明矩陣的行數量等於矩陣的秩與零空間維度之和^[18]。

方塊矩陣

主條目：方塊矩陣

行數與列數相同的矩陣稱為方塊矩陣，簡稱方陣。所有${\displaystyle n}$維的方塊矩陣構成一個線性空間，這個空間對矩陣乘法也是封閉的，因此也是一個代數。方陣${\displaystyle \mathbf {A} }$稱為可逆或非奇異的，如果存在另一個方陣${\displaystyle \mathbf {B} }$，使得

${\displaystyle \mathbf {AB} =\mathbf {I} _{n}}$

成立。這時候可以證明也有${\displaystyle \mathbf {BA} =\mathbf {I} _{n}}$成立^[19]，可將矩陣${\displaystyle \mathbf {B} }$稱為${\displaystyle \mathbf {A} }$的逆矩陣^[20]。一個矩陣${\displaystyle \mathbf {A} }$的逆矩陣如果存在的話，就是唯一的，通常記作${\displaystyle \mathbf {A} ^{-1}}$。

矩陣${\displaystyle \mathbf {A} }$的元素${\displaystyle A_{i,i}}$稱為其主對角線上的元素。方塊矩陣${\displaystyle \mathbf {A} }$的所有主對角線元素之和稱為它的跡，寫作${\displaystyle \mathrm {tr} (\mathbf {A} )}$。儘管矩陣的乘法不滿足交換律，方陣相乘時交換順序會導致乘積變化，但它們的跡不會變，即${\displaystyle \mathrm {tr} (\mathbf {AB} )=\mathrm {tr} (\mathbf {BA} )}$^[21]。除此以外，矩陣轉置的跡等於其自身的跡，${\displaystyle \mathrm {tr} (\mathbf {A} )=\mathrm {tr} (\mathbf {A} ^{\mathrm {T} })}$。

如果一個方陣只有主對角線上的元素不是0，其它都是0，那麼稱其為對角矩陣。如果主對角線上方的元素都是0，那麼稱為下三角矩陣；反之如果主對角線下方的元素都是0，那麼稱為上三角矩陣。例如${\displaystyle n=3}$的時候，這些矩陣分別寫作：

${\displaystyle {\begin{bmatrix}d_{11}&0&0\\0&d_{22}&0\\0&0&d_{33}\\\end{bmatrix}}}$（對角矩陣），${\displaystyle {\begin{bmatrix}l_{11}&0&0\\l_{21}&l_{22}&0\\l_{31}&l_{32}&l_{33}\\\end{bmatrix}}}$（下三角矩陣）和${\displaystyle {\begin{bmatrix}u_{11}&u_{12}&u_{13}\\0&u_{22}&u_{23}\\0&0&u_{33}\\\end{bmatrix}}}$（上三角矩陣）。

行列式

主條目：行列式

R²裏的一個線性轉換f將藍色圖形變成綠色圖形，面積不變，而順時針排布的向量x1和x2的變成了逆時針排布。對應的矩陣行列式是-1.

方塊矩陣${\displaystyle \mathbf {A} }$的行列式是一個將其對映到純量的函數，記作${\displaystyle \det(\mathbf {A} )}$或${\displaystyle \mathbf {|A|} }$，反映了矩陣自身的一定特性。一個方陣的行列式等於0若且唯若該方陣不可逆。系數是實數的時候，二維（三維）方陣${\displaystyle \mathbf {A} }$的行列式的絕對值表示單位面積（體積）的圖形經過${\displaystyle \mathbf {A} }$對應的線性轉換後得到的圖形的面積（體積），而它的正負則代表了對應的線性轉換是否改變空間的定向：行列式為正說明它保持空間定向，行列式為負則說明它逆轉空間定向。

2×2矩陣的行列式是

${\displaystyle {\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc}$ 。

3×3矩陣的行列式由6項組成。更高維矩陣的行列式則可以使用萊布尼茲公式寫出^[22]，或使用拉普拉斯展開由低一維的矩陣行列式遞推得出^[23]。

兩個矩陣相乘，乘積的行列式等於它們的行列式的乘積：${\displaystyle \det(\mathbf {AB} )=\det(\mathbf {A} )\cdot \det(\mathbf {B} )}$^[24]。將矩陣的一行／列乘以某個系數加到另一行／列上不改變矩陣的行列式，將矩陣的兩行／列互換則使得其行列式變號^[25]。用這兩種操作可以將矩陣變成一個上三角矩陣或下三角矩陣，而後兩種矩陣的行列式就是主對角線上元素的乘積，因此能方便地計算。運用行列式可以計算線性方程組的解（見克萊姆法則）^[26]。

特徵值與特徵向量

主條目：特徵向量

${\displaystyle n\times n}$的方塊矩陣${\displaystyle \mathbf {A} }$的一個特徵值和對應特徵向量是滿足

${\displaystyle \mathbf {Av} =\lambda \mathbf {v} }$^[27]的純量${\displaystyle \lambda }$以及非零向量${\displaystyle \mathbf {v} }$。特徵值和特徵向量的概念對研究線性轉換很有幫助。一個線性轉換可以通過它對應的矩陣在向量上的作用來視覺化。一般來說，一個向量在經過對映之後可以變為任何可能的向量，而特徵向量具有更好的性質^[28]。假設在給定的基底下，一個線性轉換對應着某個矩陣${\displaystyle \mathbf {A} }$，如果一個向量${\displaystyle \mathbf {x} }$可以寫成矩陣的幾個特徵向量的線性組合：

${\displaystyle \mathbf {x} =c_{1}\mathbf {x} _{\lambda _{1}}+c_{2}\mathbf {x} _{\lambda _{2}}+\cdots +c_{k}\mathbf {x} _{\lambda _{k}}}$

其中的${\displaystyle \mathbf {x} _{\lambda _{i}}}$表示此向量對應的特徵值是${\displaystyle \lambda _{i}}$，那麼向量${\displaystyle \mathbf {x} }$經過線性轉換後會變成：

${\displaystyle \mathbf {Ax} =c_{1}\lambda _{1}\mathbf {x} _{\lambda _{1}}+c_{2}\lambda _{2}\mathbf {x} _{\lambda _{2}}+\cdots +c_{k}\lambda _{k}\mathbf {x} _{\lambda _{k}}}$

可以清楚地知道轉換後向量的結構。

另一個等價的特徵值定義是：純量${\displaystyle \lambda }$為特徵值，如果矩陣${\displaystyle \mathbf {A} -\lambda \mathbf {I} _{n}}$是不可逆矩陣。根據不可逆矩陣的性質，這個定義也可以用行列式方程式描述：${\displaystyle \lambda }$為特徵值，如果

${\displaystyle \det(\lambda \mathbf {I} _{n}-\mathbf {A} )=0.\ }$^[29]這個定義中的行列式可以展開成一個關於${\displaystyle \lambda }$的n階多項式，叫做矩陣A的特徵多項式，記為${\displaystyle p_{\mathbf {A} }}$。特徵多項式是一個首一多項式（最高次項系數是1的多項式）。它的根就是矩陣${\displaystyle \mathbf {A} }$特徵值^[30]。哈密爾頓－凱萊定理說明，如果用矩陣${\displaystyle \mathbf {A} }$本身代替多項式中的不定元${\displaystyle \lambda }$，那麼多項式的值是零矩陣^[31]：

${\displaystyle p_{\mathbf {A} }(\mathbf {A} )=0}$。

對稱

主條目：對稱矩陣

轉置等於自己的矩陣，即滿足${\displaystyle \mathbf {A} =\mathbf {A} ^{\mathrm {T} }}$的方塊矩陣${\displaystyle \mathbf {A} }$叫做對稱矩陣。滿足${\displaystyle \mathbf {A} =-\mathbf {A} ^{\mathrm {T} }}$的矩陣稱為反對稱矩陣。在複系數矩陣中，則有埃爾米特矩陣的概念：滿足${\displaystyle \mathbf {A} =\mathbf {A} ^{*}}$的方塊矩陣稱為埃爾米特矩陣，其中的${\displaystyle \mathbf {A} ^{*}}$表示${\displaystyle \mathbf {A} }$的共軛轉置矩陣。

根據譜定理，實對稱矩陣和復埃爾米特矩陣擁有特徵基，即由矩陣的特徵向量組成的基底。因此任何向量都能表示成矩陣特徵向量的線性組合。此外，這兩類矩陣的特徵值都是實數^[32]。

正定性

矩陣表達式	${\displaystyle {\begin{bmatrix}{\frac {1}{4}}&0\\0&-{\frac {1}{4}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\frac {1}{4}}&0\\0&{\frac {1}{4}}\end{bmatrix}}}$
正定性	不定矩陣	正定矩陣
對應二次型	${\displaystyle Q(x,y)={\frac {1}{4}}(x^{2}-y^{2})}$	${\displaystyle Q(x,y)={\frac {1}{4}}(x^{2}+y^{2})}$
取值圖像
說明	正定矩陣對應的二次型的取值範圍永遠是正的， 不定矩陣對應的二次型取值則可正可負

主條目：正定矩陣

${\displaystyle n\times n}$的實對稱矩陣${\displaystyle \mathbf {A} }$如果滿足對所有非零向量${\displaystyle \mathbf {x} \in \mathbf {R} ^{n}}$，對應的二次型

${\displaystyle Q(\mathbf {x} )=\mathbf {x} ^{\mathrm {T} }\mathbf {Ax} }$

函數值都是正數，就稱${\displaystyle \mathbf {A} }$為正定矩陣。類似地還有半正定矩陣、負定矩陣、不定矩陣等概念^[33]。對稱矩陣的正定性與其特徵值密切相關。矩陣是正定的若且唯若其特徵值都是正數^[34]。

矩陣的計算

矩陣在許多學科領域中都有應用，在很多時候，除了需要知道矩陣的理論性質以外，還需要計算矩陣的數值。為了矩陣的計算能夠足夠精確與快捷，數值線性代數中專門有研究矩陣的數值計算方法^[35]。與其它的數值計算一樣，矩陣的數值計算注重的主要也是演算法的複雜度和數值穩定性。矩陣的數值計算可以使用直接計算，也可以用迭代演算法，例如在計算方塊矩陣的特徵值時，可以從一個非零向量${\displaystyle x_{0}}$開始，通過特定迭代方法得到一個逼近某個特徵向量的向量序列^[36]。

測量一個演算法的複雜度是指估計此演算法需要的基本運算如數字的加法和乘法的次數，或者找出它的一個上界。例如按照定義計算的話，兩個${\displaystyle n}$階方陣的乘法需要${\displaystyle n^{3}}$次數字乘法計算，因為其乘積是一個${\displaystyle n}$階方陣，有${\displaystyle n^{2}}$個元素，計算每個元素需要${\displaystyle n}$次數字乘法。如果使用施特拉森演算法的話，可以將數字乘法的次數減低到大約${\displaystyle n^{2.8}}$次^[37]。此外，程式語言或環境本身對演算法的複雜度也會有影響。

某些特殊類型的矩陣攜帶的數據量比一般矩陣要少，同時帶來的資訊量比一般矩陣多。一個重要的例子是稀疏矩陣，這類矩陣中絕大部分的元素是零。有關稀疏矩陣的計算，如計算稀疏矩陣${\displaystyle \mathbf {A} }$的線性方程組${\displaystyle \mathbf {Ax} =\mathbf {b} }$時，可以使用一些專用於稀疏矩陣的特殊演算法（比如共軛梯度法^[38]），減低計算複雜度。

演算法的數值穩定性是指輸入值的小變化不會讓計算結果產生很大偏差。例如計算矩陣的逆時，可以用以下的演算法（其中${\displaystyle \mathrm {adj} (\mathbf {A} )}$表示${\displaystyle \mathbf {A} }$的伴隨矩陣，${\displaystyle \mathrm {det} (\mathbf {A} )}$表示${\displaystyle \mathbf {A} }$的行列式）

${\displaystyle \mathbf {A} ^{-1}={\frac {\operatorname {adj} (\mathbf {A} )}{\det(\mathbf {A} )}}}$

這個演算法在${\displaystyle \mathbf {A} }$的行列式接近0的時候會引起很大的捨入誤差^[39]。而如果使用全選軸元的高斯消元法求逆，則在複雜度降低的同時能夠避免捨入誤差，保證數值穩定性。

矩陣分解

主條目：矩陣分解、對角化、高斯消元法和巴萊斯演算法

矩陣研究的一大方向是將一般的矩陣用一些比較「簡單」的矩陣來表示。這種表示方式稱為矩陣的轉換與分解。矩陣轉換與分解的方法有很多，它們的目的都是希望化簡後的矩陣保持原矩陣的某些性質，比如行列式、秩或逆矩陣，而形式相對簡單，因而能用容易地進行討論和計算，或者能使得某些演算法更易執行。

LU分解將矩陣分解為一個下三角矩陣${\displaystyle \mathbf {L} }$和一個上三角矩陣${\displaystyle \mathbf {U} }$的乘積^[40]。分解後的矩陣可以方便某些問題的解決。例如解線性方程組時，如果將系數矩陣${\displaystyle \mathbf {A} }$分解成${\displaystyle \mathbf {A} =\mathbf {LU} }$的形式，那麼方程式的求解可以分解為求解${\displaystyle \mathbf {Ly} =\mathbf {b} }$和${\displaystyle \mathbf {Ux} =\mathbf {y} }$兩步，而後兩個方程式可以十分簡潔地求解（詳見三角矩陣中「向前與向後替換」一節）。又例如在求矩陣的行列式時，如果直接計算一個矩陣${\displaystyle \mathbf {A} }$的行列式，需要計算大約${\displaystyle (n+1)!}$次加法和乘法；而如果先對矩陣做${\displaystyle \mathbf {LU} }$分解，再求行列式，就只需要大約${\displaystyle n^{3}}$次加法和乘法，大大降低了計算次數。這是因為做${\displaystyle \mathbf {LU} }$分解的複雜度大約是${\displaystyle n^{3}}$次，而後注意到${\displaystyle \mathbf {L} }$和${\displaystyle \mathbf {U} }$是三角矩陣，所以求它們的行列式只需要將主對角線上元素相乘即可。

若爾當矩陣，其中灰色框內的是若爾當塊

高斯消元法也是一種矩陣分解方法。通過初等轉換操作，可以將任何矩陣變為階梯形矩陣，而每個操作可以看做是將矩陣乘上一個特定的初等矩陣^[41]。奇異值分解則是另一種分解方法，將一個矩陣表示成3個矩陣的乘積：${\displaystyle \mathbf {A} =\mathbf {UDV} }$。其中${\displaystyle \mathbf {U} }$和${\displaystyle \mathbf {V} }$是么正矩陣，${\displaystyle \mathbf {D} }$是對角矩陣。

特徵分解是將一個矩陣${\displaystyle \mathbf {A} }$寫成${\displaystyle \mathbf {PDP} ^{-1}}$的形式，其中${\displaystyle \mathbf {P} }$是一個可逆矩陣，${\displaystyle \mathbf {D} }$是對角矩陣^[42]。如果${\displaystyle \mathbf {A} }$的特徵分解存在，就稱它是可對角化的矩陣。不能對角化的矩陣，也有類似的分解方式。任意的矩陣${\displaystyle \mathbf {A} }$都可以寫成${\displaystyle \mathbf {PJP} ^{-1}}$的形式，其中的矩陣${\displaystyle \mathbf {J} }$是若爾當標準型。若爾當標準型是矩陣的一種，它與對角矩陣類似，只不過主對角線上的元素不是數值，而是若爾當塊：主對角線上為同一元素${\displaystyle \lambda _{i}}$，主對角線右上一行的次對角線上都是1，其它元素都是0的矩陣（見右圖）^[43]。特徵分解可以方便計算矩陣的冪次和多項式，如要計算${\displaystyle \mathbf {A} ^{n}}$：

${\displaystyle \mathbf {A} ^{n}=(\mathbf {PDP} ^{-1})^{n}=\mathbf {PDP} ^{-1}\mathbf {PDP} ^{-1}\ldots \mathbf {PDP} ^{-1}=\mathbf {PD} ^{n}\mathbf {P} ^{-1}}$

而其中對角矩陣的冪次${\displaystyle \mathbf {D} ^{n}}$要比${\displaystyle \mathbf {A} ^{n}}$容易計算得多。同理還可計算矩陣指數：${\displaystyle e^{\mathbf {A} }}$（在線性微分方程式中有應用）、矩陣對數和矩陣的平方根^[44]。為了提高演算法的數值穩定性，還有舒爾分解等矩陣分解方法^[45]。

矩陣的推廣

矩陣的元素除了可以是實數和複數以外，也可以任意環或體中元素。線上性代數中，矩陣的性質可以經由有限維的線性空間中的線性轉換定義。更廣泛的，無限維空間中的線性算子，則可以定義更廣泛的無窮維矩陣。矩陣的另一種推廣是張量。純量可以看成零維方式排列的數據（只有一個「點」），向量可以看成是一維方式排列的數據（若干個「點」排成的「線段」），矩陣可以看成是二維方式排列的數據（若干個「線段」排成的「矩形」），而張量的概念則包括了這幾種排列方式。在張量的概念中，純量是零維張量，向量是一維張量，矩陣是二維張量，而更高維方式排列的數據方式就是高維張量^[46]。

一般體和環上的矩陣

矩陣的元素除了可以是實數和複數以外，還可以是任何能夠使得矩陣的運算律成立的元素。首先，矩陣的元素可以是任意一個體（即能夠進行「加減乘除」運算的集合）中元素。例如編碼理論中會出現系數為有限體中元素的矩陣，以及有理數系數的矩陣。如果矩陣的系數所在體${\displaystyle \mathbf {K} }$不是代數閉體，那麼在求矩陣的特徵值時，由於特徵值是相應的特徵多項式的根，可能不在系數體${\displaystyle \mathbf {K} }$中，而是在系數體的某個擴張體L中。反過來，如果考慮擴張體${\displaystyle \mathbf {L/K} }$，以及${\displaystyle \mathbf {L} }$中的一個元素${\displaystyle \alpha }$，以及${\displaystyle \mathbf {L} }$中線性轉換${\displaystyle m_{\alpha }:\,x\mapsto \alpha x}$，那麼由於${\displaystyle m_{\alpha }}$也是一個${\displaystyle \mathbf {K} }$-線性轉換，它可以表示成一個${\displaystyle n\times n}$的${\displaystyle \mathbf {K} }$系數矩陣${\displaystyle X_{\alpha }}$，其中的${\displaystyle n}$是擴張體${\displaystyle \mathbf {L/K} }$的階數。${\displaystyle \alpha }$是這個矩陣的特徵值，這個矩陣的特徵多項式${\displaystyle p_{X_{\alpha }}}$是${\displaystyle \alpha }$在${\displaystyle \mathbf {K} }$中的最小多項式${\displaystyle \operatorname {min} _{\mathbf {K} }(\alpha )}$的冪次：

${\displaystyle p_{X_{\alpha }}=\left(\operatorname {min} _{\mathbf {K} }(\alpha )\right)^{r}\,}$。其中的${\displaystyle r}$是擴張體${\displaystyle \mathbf {L/K} }$ ${\displaystyle (\alpha )}$的階數^[47]。

更一般的情況是矩陣的元素屬於某個環${\displaystyle \mathbf {R} }$^[48]。環是比體更廣泛的概念，只要求其中元素能夠進行加減法和乘法運算（不一定能定義除法）。給定一個環${\displaystyle \mathbf {R} }$，${\displaystyle {\mathcal {M}}(m,n,\mathbf {R} )}$中的矩陣之間可以相互加減以及相乘，所以${\displaystyle {\mathcal {M}}(m,n,\mathbf {R} )}$關於矩陣的加法和乘法也構成一個環，稱為矩陣環。${\displaystyle n}$維方陣的環${\displaystyle {\mathcal {M}}(n,\mathbf {R} )}$與左${\displaystyle \mathbf {R} }$-模${\displaystyle \mathbf {R} ^{n}}$的自同態環同構^[49]。

若${\displaystyle \mathbf {R} }$是交換環，則${\displaystyle {\mathcal {M}}(m,\mathbf {R} )}$是一個帶單位元素的${\displaystyle \mathbf {R} }$-代數，滿足結合律，但不滿足交換律。其中的矩陣仍然可以用萊布尼茲公式定義行列式。一個矩陣可逆若且唯若其行列式為環${\displaystyle \mathbf {R} }$中的可逆元素（體上的矩陣可逆只需行列式不等於0）^[50]。

矩陣與線性轉換

前面已經提到，所有${\displaystyle \mathbf {R} ^{n}\rightarrow \mathbf {R} ^{m}}$的線性轉換都對應着一個${\displaystyle {\mathcal {M}}(m,n,\mathbf {R} )}$中的矩陣。更一般地，給定了基底後，任意兩個有限維線性空間之間的線性對映${\displaystyle f:\mathbf {V} \rightarrow \mathbf {W} }$也對應着一個矩陣${\displaystyle \mathbf {A} _{f}=(a_{ij})}$。設空間${\displaystyle \mathbf {V} }$和${\displaystyle \mathbf {W} }$的基底分別是${\displaystyle \mathbf {v} _{1},\ldots ,\mathbf {v} _{n}}$和${\displaystyle \mathbf {w} _{1},\ldots ,\mathbf {w} _{m}}$，那麼

對任意 ${\displaystyle j=1,\ldots ,n}$，${\displaystyle f(\mathbf {v} _{j})=\sum _{i=1}^{m}a_{i,j}\mathbf {w} _{i}}$

矩陣${\displaystyle \mathbf {A} _{f}}$實際上「記錄」了${\displaystyle \mathbf {V} }$中每個基底向量經過轉換後得到的${\displaystyle \mathbf {W} }$中的像在基底${\displaystyle (\mathbf {w} _{1},\ldots ,\mathbf {w} _{m})}$下的形式。要注意矩陣的內容取決於基底的選擇。可以說，矩陣是線性轉換f在特定「角度」（基底）下的「素描」。不同的「角度」下，描述${\displaystyle f}$的矩陣是不同的，但這些矩陣都是相似矩陣^[51]。與矩陣有關的基本概念都可以用線性轉換的層面來解釋，比如一個矩陣的轉置可以用f的對偶轉換${\displaystyle f^{*}:\mathbf {W} ^{*}\rightarrow \mathbf {V} ^{*}}$來表示^[52]。

當矩陣的元素是帶單位元素的環${\displaystyle \mathbf {R} }$中的元素時，${\displaystyle m\times n}$的${\displaystyle \mathbf {R} }$-矩陣對應的則是${\displaystyle \mathbf {R} }$-自由模${\displaystyle \mathbf {R} ^{m}}$和${\displaystyle \mathbf {R} ^{n}}$之間的${\displaystyle \mathbf {R} }$-線性轉換。${\displaystyle n=m}$的時候，這些${\displaystyle \mathbf {R} }$-線性轉換可以相互複合，因此${\displaystyle n}$維的${\displaystyle \mathbf {R} }$-矩陣環能夠與${\displaystyle \mathbf {R} }$-自同態環${\displaystyle \mathbf {R} ^{n}}$同構。

矩陣群

主條目：矩陣群

群是比環更寬泛的代數結構，只需要集合配備一個滿足結合律的二元運算，即將兩個群內元素對映到群內一元素的運算。矩陣群是指矩陣關於矩陣乘法組成的群^[53]。顯然，只有方塊矩陣才能構成乘法群。所有${\displaystyle n}$維的可逆方陣構成一個群，稱為${\displaystyle n}$階一般線性群。由於群內每個元素都必須是可逆的，任意的矩陣群都必然是一般線性群的子群。

能夠在矩陣乘法和求逆矩陣運算下保持的性質都可以用來刻畫一定的矩陣群。例如所有行列式為1的矩陣可以構成一個群，稱為${\displaystyle n}$階特殊線性群^[54]。所有${\displaystyle n}$維的正交矩陣，即滿足：

${\displaystyle \mathbf {M} ^{\mathrm {T} }\mathbf {M} =\mathbf {I} }$

的矩陣${\displaystyle \mathbf {M} }$也構成一個群，稱為${\displaystyle n}$階正交群^[55]。正交矩陣得名於它在${\displaystyle \mathbf {R} ^{n}}$中對應的線性轉換具有保角性，也就是說對基本的點積，滿足

${\displaystyle (\mathbf {Mv} )\cdot (\mathbf {Mw} )=\mathbf {v} \cdot \mathbf {w} }$^[56]

每個有限群都同構於一個矩陣群。實際上，每個有限群都同構於某個置換群的子群，而每個置換群都同構於一個矩陣群（見置換群的正則群表示^[57]）鑑於矩陣群的性質可以通過與矩陣相關的更多手段更好地理解，常常通過研究矩陣群來研究一個有限群。相關的理論稱為群表示論。

無限維矩陣

主條目：無限維矩陣

無窮維矩陣可以指行數或列數無窮大，或兩者都是無窮大的矩陣^[58]。儘管這樣的矩陣無法完整寫出，但只要知道每行每列的元素的值，仍然可以對它進行矩陣操作和運算。這裏矩陣的行數和列數甚至不一定需要是可數集。需要注意的是，無窮維矩陣的乘法涉及到無窮級數求和，因此只有在相關的無窮級數收斂的時候，才能定義矩陣的乘積^[59]。無限維矩陣也可以是方塊矩陣，定義為行標記集合與列標記集合相同的矩陣（如${\displaystyle \mathbb {N} \times \mathbb {N} }$）^[60]。

無限矩陣無法定義通常意義上的行列式，因此可逆矩陣不一定是方塊矩陣，同理，么正矩陣也不一定要是方塊矩陣^[61]。

空矩陣

主條目：空矩陣

空矩陣是指行數或列數為零的矩陣。^[62][63]空矩陣的定義可以完善一些關於零維空間的約定。包括約定一個矩陣與空矩陣相乘得到的也是空矩陣，兩個${\displaystyle n\times 0}$和${\displaystyle 0\times p}$的空矩陣相乘是一個${\displaystyle n\times p}$的零矩陣（所有元素都是零的矩陣）。0×0的空矩陣的行列式約定為1，所以它也可以有逆矩陣，約定為它自己^[64]。

分塊矩陣

分塊矩陣是指一個大矩陣分割成「矩陣的矩陣」。舉例，以下的矩陣

${\displaystyle P={\begin{bmatrix}1&2&3&2\\1&2&7&5\\4&9&2&6\\6&1&5&8\end{bmatrix}}}$

可分割成4個2×2的矩陣

${\displaystyle P_{11}={\begin{bmatrix}1&2\\1&2\end{bmatrix}},P_{12}={\begin{bmatrix}3&2\\7&5\end{bmatrix}},P_{21}={\begin{bmatrix}4&9\\6&1\end{bmatrix}},P_{22}={\begin{bmatrix}2&6\\5&8\end{bmatrix}}}$

${\displaystyle P={\begin{bmatrix}P_{11}&P_{12}\\P_{21}&P_{22}\end{bmatrix}}}$。將矩陣分塊可以使得矩陣結構清晰，在某些時候可以方便運算、證明。兩個大小相同、分塊方式也相同的矩陣可以相加。行和列的塊數符合矩陣乘法要求時，分塊矩陣也可以相乘。將矩陣分塊相乘的結果與直接相乘是一樣的。用分塊矩陣求逆，可以將高階矩陣的求逆轉化為多次低階矩陣的求逆^[65]。

應用

矩陣在許多領域都應用廣泛。有些時候用到矩陣是因為其表達方式緊湊，例如在博弈論和經濟學中，會用收益矩陣來表示兩個博弈物件在各種決策方式下的收益^[66]。文字挖掘和索引典組譯的時候，比如在TF-IDF方法中，也會用到檔案項矩陣來追蹤特定詞彙在多個檔案中的出現頻率^[67]。

複數可以用實系數的2×2矩陣表示：

${\displaystyle a+ib\leftrightarrow {\begin{bmatrix}a&-b\\b&a\end{bmatrix}},}$

這種表示法與複數的加減法、乘法都相容。比如，2×2的旋轉矩陣可以用來表示模長為1的複數，一個向量乘以此旋轉矩陣可以視作一個複數乘以該模長為1的複數。對四元數也有類似的矩陣表達^[68]。

早期的密碼技術如希爾密碼也用到矩陣。然而，矩陣的線性性質使這類密碼相對容易破解^[69]。電腦圖像處理也會用到矩陣來表示處理物件，並且用放射旋轉矩陣來計算物件的轉換，實現三維物件在特定二維螢幕上的投影^[70]。多項式環上的矩陣在控制論中有重要作用。

化學中也有矩陣的應用，特別在使用量子理論討論分子鍵和光譜的時候。具體例子有解羅特漢方程式時用重疊矩陣和福柯矩陣來得到哈特里－福克方法中的分子軌道。

圖論

一個無向圖的鄰接矩陣${\displaystyle {\begin{bmatrix}1&1&0\\1&0&1\\0&1&0\end{bmatrix}}}$。

圖論中可以用矩陣描述一個有限圖^[71]。這個矩陣叫做相關矩陣的鄰接矩陣，記錄了圖的每兩個頂點之間是否有邊連接。對簡單圖來說，鄰接矩陣的元素只取兩個值：0和1,第${\displaystyle i}$列第${\displaystyle j}$行上取值為0，表示沒有從第${\displaystyle i}$個頂點連到第${\displaystyle j}$個頂點的邊，取值為1則說明有。如果是一般情況的話，第${\displaystyle i}$列第${\displaystyle j}$ 行上的取值是從第${\displaystyle i}$個頂點連到第j個頂點的邊的數目。距離矩陣則是表示圖中各頂點之間距離的矩陣^[72]。在研究互聯網等複雜網絡的時候，鄰接矩陣常常會是稀疏矩陣。因此網絡理論中有專門研究稀疏矩陣的方面。

數學分析

在多元函數微積分學中，對二階偏導數存在的函數${\displaystyle f:\mathbf {R} ^{n}\rightarrow \mathbf {R} }$，可以定義其海森矩陣^[73]：

${\displaystyle H(f)(x)=\left[{\frac {\partial ^{2}f}{\partial x_{i}\,\partial x_{j}}}(x)\right]}$。

${\displaystyle n=2}$時，海森矩陣${\displaystyle {\begin{bmatrix}2&0\\0&-2\end{bmatrix}}}$的特徵值一正一負，說明函數${\displaystyle f(x,y)=x^{2}-y^{2}}$在${\displaystyle (x=0,y=0)}$處有一個鞍點（紅色點）

嚴格來說，僅當函數在某一點上的二階偏導數存在，才能定義這一點上的海森矩陣。海森矩陣給出了函數在這一點的變化率方面的資訊。當給定的點${\displaystyle \mathbf {x} =(x_{1},\ldots ,x_{n})}$是函數平穩點（即函數${\displaystyle f}$在這一點上的一階偏導數${\displaystyle {\frac {\partial f}{\partial x_{i}}}}$都是0）時，就需要利用海森矩陣來檢視函數在這一點周圍的增長特性。多元函數在點${\displaystyle \mathbf {x} }$的泰勒展開是：

${\displaystyle f(x+h)=f(x)+\nabla f(x)\cdot h+{\frac {1}{2}}h^{T}H(f)(x)h+\circ \left(\|x\|^{3}\right)}$

如果函數在點x的一階偏導數都是0，那麼${\displaystyle \nabla f=0}$，所以函數在x附近的變化率取決於海森矩陣${\displaystyle H(f)(x)}$的性質。如果${\displaystyle H(f)(x)}$是正定矩陣，那麼函數在點x取得局部最小值，如果是負定矩陣，則函數在x取得局部最大值。在這類情況下，關於函數f的條件最佳化問題可以轉變為關於海森矩陣的二次規劃問題^[74]。

矩陣在多元函數微積分中的另一個應用是雅可比矩陣。函數${\displaystyle f:\mathbf {R} ^{n}\rightarrow \mathbf {R} ^{m}}$在某一點x上的一階偏導數存在時，可以定義它在這點上的雅可比矩陣^[75]：

${\displaystyle J_{f}(x)=\left[{\frac {\partial f_{i}}{\partial x_{j}}}(x)\right]_{1\leq i\leq m,1\leq j\leq n}}$。如果${\displaystyle n>m}$，而${\displaystyle J_{f}(x)}$又是滿秩矩陣（秩等於${\displaystyle m}$）的話，根據反函數定理，可以找到函數${\displaystyle f}$在x附近的一個局部的反函數^[76]。

偏微分方程式理論中，二階擬線性偏微分方程式可以根據最高次偏導項系數構成的矩陣的正定性分類。假設有一個二階擬線性偏微分方程式：

${\displaystyle (\mathbf {E} )\qquad \qquad \sum _{1\leqslant i,j\leqslant n}a_{ij}{\frac {\partial ^{2}f}{\partial x_{i}\,\partial x_{j}}}+\sum _{i=1}^{n}b_{i}{\frac {\partial f}{\partial x_{i}}}+cf=g\qquad }$ 並假設${\displaystyle a_{ij}=a_{ji}}$

記矩陣${\displaystyle \mathbf {A} =\left[a_{ij}\right]_{1\leqslant i,j\leqslant n}}$。如果矩陣${\displaystyle \mathbf {A} }$是正定或負定矩陣，那麼就稱方程式${\displaystyle (\mathbf {E} )}$為橢圓形偏微分方程式；如果${\displaystyle \mathbf {A} }$不可逆，就稱${\displaystyle (\mathbf {E} )}$為拋物形偏微分方程式，如果${\displaystyle \mathbf {A} }$可逆而且恰有${\displaystyle n-1}$個特徵值同號，就稱${\displaystyle (\mathbf {E} )}$為雙曲型偏微分方程式。其它情況下也稱${\displaystyle (\mathbf {E} )}$為超雙曲形偏微分方程式。不同類型的方程式解的形式也不一樣^[77]。

用數值方法解偏微分方程式時更需要用到矩陣。一個重要的方法是有限元方法，在求解各種物理中遇到的偏微分方程式時廣泛使用。有限元方法的基本思想是用一系列「簡單」函數的線性組合來「逼近」偏微分方程式的精確解。這些「簡單」函數通常是指將求解區域分割成一定數量的「小塊」後，僅在某一「小塊」上非零的分段線性函數。選定了網格和「簡單」函數後，可以求解關於剛度矩陣的方程式得到近似解。有限元理論中證明了在滿足一定的條件下，近似解將隨着網格趨於精細而弱收斂到精確解^[78][79]。

機率論與統計

機率論中常用到隨機矩陣，即列向量是機率向量（即所有的元素都在0和1之間，並且加起來等於1的向量）的矩陣。隨機矩陣可用來定義有限機率空間中的馬可夫鏈。設隨機變量${\displaystyle X_{n}}$是某個馬可夫鏈在${\displaystyle t=n}$時刻的狀態，所有可能的狀態${\displaystyle S=\left\{s_{1},s_{2},\cdots ,s_{m}\right\}}$稱為狀態空間，那麼隨機矩陣${\displaystyle M_{n}^{n+1}}$則記錄了假設已知${\displaystyle X_{n}}$的可能情況下${\displaystyle X_{n+1}}$做各種取值的可能性^[80]。${\displaystyle M_{n}^{n+1}}$的第${\displaystyle i}$列第${\displaystyle j}$行上的元素表示當${\displaystyle X_{n}=s_{j}}$的時候，${\displaystyle X_{n+1}=s_{i}}$的可能性。${\displaystyle M_{n}^{n+1}}$的第${\displaystyle j}$列記錄了從${\displaystyle X_{n}=s_{j}}$轉移到${\displaystyle X_{n+1}}$各種狀態的可能性。所以${\displaystyle M_{n}^{n+1}}$叫做${\displaystyle t=n}$時刻的轉移矩陣。如果馬可夫鏈的轉移矩陣不隨時刻變化，則稱為齊次馬可夫鏈。這時馬可夫鏈的吸引態可以通過計算轉移矩陣的特徵向量得到^[81]。

統計學中也會用到各種不同的矩陣。敘述統計學中常常需要用矩陣的形式來描述數據樣本，顯得更為緊湊。幾個隨機變量的協方差矩陣表示它們之間的協方差關係，在某種程度上表示了它們相互間的關聯程度（但不絕對）^[82]。

統計學中用到矩陣的另一個地方是線性迴歸中的最小平方法分析。當觀測到隨機樣本${\displaystyle (Y_{i},X_{i1},\ldots ,X_{ip}),\,i=1,\ldots ,n}$時，線性迴歸法的目標是希望找到以下的線性關係：

${\displaystyle Y_{i}=\beta _{0}+\beta _{1}X_{i1}+\beta _{2}X_{i2}+\ldots +\beta _{p}X_{ip}+\varepsilon _{i},\qquad i=1,\ldots ,n}$

即將變數${\displaystyle \mathbf {Y} }$表示成${\displaystyle \mathbf {X} }$的分量的線性組合與一個已知的隨機誤差的和。這個表示可以寫成矩陣的形式，並利用矩陣的奇異值分解來分析^[83]。

另一種隨機矩陣（random matrix）是指每個元素都是隨機變量的矩陣，這些隨機變量可以都遵循同一個分佈，或各自遵循不同的分佈。一個常見的例子是全部元素都是相互獨立的標準正態分佈隨機變量的隨機矩陣。這種隨機矩陣在數論和物理中也有應用^[84][85]。

物理學上的對稱性及線性轉換

更多資訊：對稱性 (物理學)

線性轉換及其所對應的對稱，在現代物理學中有着重要的角色。例如，在量子場論中，基本粒子是由狹義相對論的勞侖茲群所表示，具體來說，即它們在旋量群下的表現。內含鮑利矩陣及更通用的狄拉克矩陣的具體表示，在費米子的物理描述中，是一項不可或缺的構成部分，而費米子的表現可以用旋量來表述^[86]。描述最輕的三種夸克時，需要用到一種內含特殊么正群SU(3)的群論表示；物理學家在計算時會用一種更簡便的矩陣表示，叫蓋爾曼矩陣，這種矩陣也被用作SU(3)規範群，而強核力的現代描述──量子色動力學的基礎正是SU(3)。還有卡比博-小林-益川矩陣（CKM矩陣）：在弱相互作用中重要的基本夸克態，與指定粒子間不同質素的夸克態不一樣，但兩者卻是成線性關係，而CKM矩陣所表達的就是這一點^[87]。

量子態的線性組合

1925年海森堡提出第一個量子力學模型時，使用了無限維矩陣來表示理論中作用在量子態上的算子^[88]。這種做法在矩陣力學中也能見到。例如密度矩陣就是用來刻畫量子系統中「純」量子態的線性組合表示的「混合」量子態^[89]。

另一種矩陣是用來描述構成實驗粒子物理基石的散射實驗的重要工具。當粒子在加速器中發生碰撞，原本沒有相互作用的粒子在高速運動中進入其它粒子的作用區，動量改變，形成一系列新的粒子。這種碰撞可以解釋為結果粒子狀態和入射粒子狀態線性組合的純量積。其中的線性組合可以表達為一個矩陣，稱為S矩陣，其中記錄了所有可能的粒子間相互作用^[90]。

簡正模式

矩陣在物理學中的另一類泛應用是描述線性耦合調和系統。這類系統的運動方程式可以用矩陣的形式來表示，即用一個質素矩陣乘以一個廣義速度來給出運動項，用力矩陣乘以位移向量來刻畫相互作用。求系統的解的最佳方法是將矩陣的特徵向量求出（通過對角化等方式），稱為系統的簡正模式。這種求解方式在研究分子內部動力學模式時十分重要：系統內部由化學鍵結合的原子的振動可以表示成簡正振動模式的疊加^[91]。描述力學振動或電路振盪時，也需要使用簡正模式求解^[92]。

幾何光學

在幾何光學裏，可以找到很多需要用到矩陣的地方。幾何光學是一種忽略了光波波動性的近似理論，這理論的模型將光線視為幾何射線。採用近軸近似，假若光線與光軸之間的夾角很小，則透鏡或反射元件對於光線的作用，可以表達為2×2矩陣與向量的乘積。這向量的兩個分量是光線的幾何性質（光線的斜率、光線跟光軸之間在主平面（英語：principal plane）的垂直距離）。這矩陣稱為光線傳輸矩陣，內中元素編碼了光學元件的性質。對於折射，這矩陣又細分為兩種：「折射矩陣」與「平移矩陣」。折射矩陣描述光線遇到透鏡的折射行為。平移矩陣描述光線從一個主平面傳播到另一個主平面的平移行為。

由一系列透鏡或反射元件組成的光學系統，可以很簡單地以對應的矩陣組合來描述其光線傳播路徑。^[93]

電子學

在電子學裏，傳統的網目分析（英語：mesh analysis）或節點分析會獲得一個線性方程組，這可以以矩陣來表示與計算。

很多種電子元件的電路行為可以用矩陣來描述。設置${\displaystyle A}$為輸入向量，其兩個分量為輸入電壓${\displaystyle v_{1}}$與輸入電流${\displaystyle i_{1}}$。設置${\displaystyle B}$為輸出向量，其兩個分量為輸出電壓${\displaystyle v_{2}}$與輸出電流${\displaystyle i_{2}}$。這電子元件的電路行為可以描述為${\displaystyle B=H\cdot A}$；其中，${\displaystyle H}$是2×2矩陣，內有一個阻抗元素${\displaystyle h_{12}}$、一個導納元素${\displaystyle h_{21}}$、兩個無量綱元素${\displaystyle h_{11}}$與${\displaystyle h_{22}}$。這樣，電路的計算可以約化為矩陣計算。

參見

• 矩陣論專有名詞表：有關矩陣論所用到的名詞的定義
• 方塊矩陣
• 矩陣範數
• 雅可比矩陣

註釋與參考

註腳

1. 董可榮 2007, 第3節
2. Shen, Crossley & Lun 1999
3. 克萊因 2002, 第33章第4節
4. Hawkins 1975
5. The Collected Mathematical Papers of James Joseph Sylvester: 1837–1853, Paper 37 （頁面存檔備份，存於互聯網檔案館）, p. 247
6. Cayley 1889, vol. II, p. 475–496
7. Dieudonné, ed. 1978, Vol. 1, Ch. III, p. 96
8. 周建華. 《矩陣》. 台灣: 中央圖書出版社. 2002. ISBN 9789576374913 （中文）.
9. Brown 1991, Definition I.2.1 (addition), Definition I.2.4 (scalar multiplication), and Definition I.2.33 (transpose)
10. Brown 1991, Theorem I.2.6
11. Brown 1991, Definition I.2.20
12. 林志興 & 楊忠鵬 2010
13. Horn & Johnson 1985, Ch. 4 and 5
14. Brown 1991, I.2.21 and 22
15. Greub 1975, Section III.2
16. Brown 1991, Definition II.3.3
17. Greub 1975, Section III.1
18. Brown 1991, Theorem II.3.22
19. Brown 1991, Definition I.5.13
20. Brown 1991, Definition I.2.28
21. 這個結論容易從矩陣乘法的定義獲得：

    ${\displaystyle \scriptstyle \operatorname {tr} ({\mathsf {AB}})=\sum _{i=1}^{m}\sum _{j=1}^{n}A_{ij}B_{ji}=\operatorname {tr} ({\mathsf {BA}})}$。

22. Brown 1991, Definition III.2.1
23. Mirsky 1990, Theorem 1.4.1
24. Brown 1991, Theorem III.2.12
25. Brown 1991, Corollary III.2.16
26. Brown 1991, Theorem III.3.18
27. Brown 1991, Definition III.4.1
28. Steven A. Leduc [[#CITEREFSteven A. Leduc|]], 第293頁
29. Brown 1991, Definition III.4.9
30. Brown 1991, Corollary III.4.10
31. 王萼芳 1997, 4.2，定理3，第247頁
32. Horn & Johnson 1985, Theorem 2.5.6
33. Horn & Johnson 1985, Chapter 7
34. Horn & Johnson 1985, Theorem 7.2.1
35. Bau III & Trefethen 1997
36. Householder 1975, Ch. 7
37. Golub & Van Loan 1996, Algorithm 1.3.1
38. Golub & Van Loan 1996, Chapters 9 and 10, esp. section 10.2
39. Golub & Van Loan 1996, Chapter 2.3
40. Press, Flannery & Teukolsky 1992
41. Stoer & Bulirsch 2002, Section 4.1
42. Horn & Johnson 1985, Theorem 2.5.4
43. Horn & Johnson 1985, Ch. 3.1, 3.2
44. Arnold & Cooke 1992, Sections 14.5, 7, 8
45. Bronson 1989, Ch. 15
46. Coburn 1955, Ch. V
47. Ash 2012, Chapter II
48. Lang 2002, Chapter XIII
49. Lang 2002, XVII.1, p. 643
50. Lang 2002, Proposition XIII.4.16
51. Greub 1975, Section III.3
52. Greub 1975, Section III.3.13
53. Baker 2003, Def. 1.30
54. Baker 2003, Theorem 1.2
55. Artin 1991, Chapter 4.5
56. Artin 1991, Theorem 4.5.13
57. Rowen 2008, Example 19.2, p. 198
58. Itõ, ed. 1987
59. Thankappan 1993
60. Thankappan 1993
61. Thankappan 1993
62. "Empty Matrix: A matrix is empty if either its row or column dimension is zero". O-Matrix v6 User Guide. （原始內容存檔於2009-04-29）.
63. Matrix - MATLAB Data Structures. system.nada.kth.se. （原始內容存檔於2009-12-28）. A matrix having at least one dimension equal to zero is called an empty matrix
64. Faliva & Zoia 2008
65. 居余馬 2002, 2.6
66. Fudenberg & Tirole 1983, Section 1.1.1
67. Manning 1999, Section 15.3.4
68. Ward 1997, Ch. 2.8
69. Stinson 2005, Ch. 1.1.5 and 1.2.4
70. Association for Computing Machinery 1979, Ch. 7
71. Godsil & Royle 2004, Ch. 8.1
72. Punnen 2002
73. Lang 1987a, Ch. XVI.6
74. Nocedal 2006, Ch. 16
75. Lang 1987a, Ch. XVI.1
76. Lang 1987a, Ch. XVI.5
77. Gilbarg & Trudinger 2001
78. Šolin 2005, Ch. 2.5
79. 伊澤爾萊斯 2005, Ch. 8
80. Latouche & Ramaswami 1999
81. Mehata & Srinivasan 1978, Ch. 2.8
82. Krzanowski 1988, Ch. 2.2., p. 60
83. Krzanowski 1988, Ch. 4.1
84. Conrey 2007
85. Zabrodin, Brezin & Kazakov et al. 2006
86. Itzykson & Zuber 1980, Ch. 2
87. 見Burgess & Moore 2007, section 1.6.3. (SU(3)), section 2.4.3.2. (Kobayashi－Maskawa matrix)
88. Schiff 1968, Ch. 6
89. Bohm 2001, sections II.4 and II.8
90. Weinberg 1995, Ch. 3
91. Wherrett 1987, part II
92. Riley, Hobson & Bence 1997, 7.17
93. Guenther 1990, Ch. 5

參考文獻

• Arnold, Vladimir I.; Cooke, Roger, Ordinary differential equations, Berlin, DE; New York, NY: Springer-Verlag, 1992, ISBN 978-3-540-54813-3
• Artin, Michael, Algebra, Prentice Hall, 1991, ISBN 978-0-89871-510-1
• Association for Computing Machinery, Computer Graphics, Tata McGraw–Hill, 1979, ISBN 978-0-07-059376-3
• Baker, Andrew J., Matrix Groups: An Introduction to Lie Group Theory, Berlin, DE; New York, NY: Springer-Verlag, 2003, ISBN 978-1-85233-470-3
• Bau III, David; Trefethen, Lloyd N., Numerical linear algebra, Philadelphia, PA: Society for Industrial and Applied Mathematics, 1997, ISBN 978-0-89871-361-9
• Bretscher, Otto, Linear Algebra with Applications 3rd, Prentice Hall, 2005
• 王萼芳, 高等代数教程 第1版, 清華大學出版社, 1997, ISBN 9787302024521
• Bronson, Richard, Schaum's outline of theory and problems of matrix operations, New York: McGraw–Hill, 1989, ISBN 978-0-07-007978-6
• Brown, William A., Matrices and vector spaces, New York, NY: M. Dekker, 1991, ISBN 978-0-8247-8419-5
• Coburn, Nathaniel, Vector and tensor analysis, New York, NY: Macmillan, 1955, OCLC 1029828
• Conrey, J. Brian, Ranks of elliptic curves and random matrix theory, Cambridge University Press, 2007, ISBN 978-0-521-69964-8
• Fudenberg, Drew; Tirole, Jean, Game Theory, MIT Press, 1983
• Gilbarg, David; Trudinger, Neil S., Elliptic partial differential equations of second order 2nd, Berlin, DE; New York, NY: Springer-Verlag, 2001, ISBN 978-3-540-41160-4
• Godsil, Chris; Royle, Gordon, Algebraic Graph Theory, Graduate Texts in Mathematics 207, Berlin, DE; New York, NY: Springer-Verlag, 2004, ISBN 978-0-387-95220-8
• Golub, Gene H.; Van Loan, Charles F., Matrix Computations 3rd, Johns Hopkins, 1996, ISBN 978-0-8018-5414-9
• Greub, Werner Hildbert, Linear algebra, Graduate Texts in Mathematics, Berlin, DE; New York, NY: Springer-Verlag, 1975, ISBN 978-0-387-90110-7
• Guenther, Robert D., Modern Optics, John Wiley, 1990, ISBN 0-471-60538-7
• Halmos, Paul Richard, A Hilbert space problem book, Graduate Texts in Mathematics 19 2nd, Berlin, DE; New York, NY: Springer-Verlag, 1982, ISBN 978-0-387-90685-0, MR 0675952
• Horn, Roger A.; Johnson, Charles R., Matrix Analysis, Cambridge University Press, 1985, ISBN 978-0-521-38632-6
• Householder, Alston S., The theory of matrices in numerical analysis, New York, NY: Dover Publications, 1975, MR 0378371
• Krzanowski, Wojtek J., Principles of multivariate analysis, Oxford Statistical Science Series 3, The Clarendon Press Oxford University Press, 1988, ISBN 978-0-19-852211-9, MR 0969370
• Itõ, Kiyosi (編), Encyclopedic dictionary of mathematics. Vol. I-IV 2nd, MIT Press, 1987, ISBN 978-0-262-09026-1, MR 0901762
• Ash, Robert B., A Course In Algebraic Number Theory (PDF), Dept. of Mathematics, University of Illinois, [2012-04-15], （原始內容存檔 (PDF)於2017-05-18）
• Lang, Serge, Analysis II, Addison-Wesley, 1969
• Lang, Serge, Calculus of several variables 3rd, Berlin, DE; New York, NY: Springer-Verlag, 1987a, ISBN 978-0-387-96405-8
• Lang, Serge, Linear algebra, Berlin, DE; New York, NY: Springer-Verlag, 1987b, ISBN 978-0-387-96412-6
• Latouche, Guy; Ramaswami, Vaidyanathan, Introduction to matrix analytic methods in stochastic modeling 1st, Philadelphia, PA: Society for Industrial and Applied Mathematics, 1999, ISBN 978-0-89871-425-8
• Manning, Christopher D.; Schütze, Hinrich, Foundations of statistical natural language processing, MIT Press, 1999, ISBN 978-0-262-13360-9
• Mehata, K. M.; Srinivasan, S. K., Stochastic processes, New York, NY: McGraw–Hill, 1978, ISBN 978-0-07-096612-3
• Mirsky, Leonid, An Introduction to Linear Algebra, Courier Dover Publications, 1990, ISBN 978-0-486-66434-7
• Nocedal, Jorge; Wright, Stephen J., Numerical Optimization 2nd, Berlin, DE; New York, NY: Springer-Verlag: 449, 2006, ISBN 978-0-387-30303-1
• Bohm, Arno, Quantum Mechanics: Foundations and Applications, Springer, 2001, ISBN 0-387-95330-2
• Burgess, Cliff; Moore, Guy, The Standard Model. A Primer, Cambridge University Press, 2007, ISBN 0-521-86036-9
• Guenther, Robert D., Modern Optics, John Wiley, 1990, ISBN 0-471-60538-7
• Itzykson, Claude; Zuber, Jean-Bernard, Quantum Field Theory, McGraw–Hill, 1980, ISBN 0-07-032071-3
• Riley, Kenneth F.; Hobson, Michael P.; Bence, Stephen J., Mathematical methods for physics and engineering, Cambridge University Press, 1997, ISBN 0-521-55506-X
• Schiff, Leonard I., Quantum Mechanics 3rd, McGraw–Hill, 1968
• Weinberg, Steven, The Quantum Theory of Fields. Volume I: Foundations, Cambridge University Press, 1995, ISBN 0-521-55001-7
• Wherrett, Brian S., Group Theory for Atoms, Molecules and Solids, Prentice–Hall International, 1987, ISBN 0-13-365461-3
• Zabrodin, Anton; Brezin, Édouard; Kazakov, Vladimir; Serban, Didina; Wiegmann, Paul, Applications of Random Matrices in Physics (NATO Science Series II: Mathematics, Physics and Chemistry), Berlin, DE; New York, NY: Springer-Verlag, 2006, ISBN 978-1-4020-4530-1
• 林志興; 楊忠鵬, 与给定矩阵A的可交换子环C(A)的一些探讨, 莆田學院學報，2010年, 17(2), 2010
• Oualline, Steve, Practical C++ programming, O'Reilly, 2003, ISBN 978-0-596-00419-4
• Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T., LU Decomposition and Its Applications, Numerical Recipes in FORTRAN: The Art of Scientific Computing (PDF) 2nd, Cambridge University Press: 34–42, 1992, （原始內容 (PDF)存檔於2009-09-06）
• Punnen, Abraham P.; Gutin, Gregory, The traveling salesman problem and its variations, Boston, MA: Kluwer Academic Publishers, 2002, ISBN 978-1-4020-0664-7
• Reichl, Linda E., The transition to chaos: conservative classical systems and quantum manifestations, Berlin, DE; New York, NY: Springer-Verlag, 2004, ISBN 978-0-387-98788-0
• Rowen, Louis Halle, Graduate Algebra: noncommutative view, Providence, RI: American Mathematical Society, 2008, ISBN 978-0-8218-4153-2
• Šolin, Pavel, Partial Differential Equations and the Finite Element Method, Wiley-Interscience, 2005, ISBN 978-0-471-76409-0
• Stinson, Douglas R., Cryptography, Discrete Mathematics and its Applications, Chapman & Hall/CRC, 2005, ISBN 978-1-58488-508-5
• Stoer, Josef; Bulirsch, Roland, Introduction to Numerical Analysis 3rd, Berlin, DE; New York, NY: Springer-Verlag, 2002, ISBN 978-0-387-95452-3
• Ward, J. P., Quaternions and Cayley numbers, Mathematics and its Applications 403, Dordrecht, NL: Kluwer Academic Publishers Group, 1997, ISBN 978-0-7923-4513-8, MR 1458894
• （中文）居余馬; 林翠琴, 线性代数, 清華大學出版社, 2002, ISBN 978-7-302-06507-4
• （中文）克萊因, 莫里斯; 著，張理京、張錦炎、江澤涵譯, 《古今数学思想》第三卷, 上海科學技術出版社, 2002, ISBN 7-5323-6172-1
• Wolfram, Stephen, The Mathematica Book 5th, Champaign, IL: Wolfram Media, 2003, ISBN 978-1-57955-022-6
• Thankappan, V. K., Quantum Mechanics 2nd, New Age International, 1993, ISBN 9788122405262
• Faliva, Mario; Zoia, Maria Grazia, Dynamic Model Analysis: Advanced Matrix Methods and Unit-Root Econometrics Representation Theorems 2nd, Berlin, DE; New York, NY: Springer-Verlag: 218, 2008, ISBN 9783540859956
• 伊澤爾萊斯, 劉曉艷，劉學深譯, 微分方程数值分析基础教程, 清華大學出版社, 2005, ISBN 9787302106524
• 董可榮, 矩阵理论的历史研究, 《山東大學》, 2007
• Bôcher, Maxime, Introduction to higher algebra, New York, NY: Dover Publications, 2004, ISBN 978-0-486-49570-5
• Cayley, Arthur, The collected mathematical papers of Arthur Cayley, I (1841–1853), Cambridge University Press: 123–126, 1889
• Dieudonné, Jean (編), Abrégé d'histoire des mathématiques 1700-1900, Paris, FR: Hermann, 1978
• Hawkins, Thomas, Cauchy and the spectral theory of matrices, Historia Mathematica, 1975, 2: 1–29, ISSN 0315-0860, MR 0469635, doi:10.1016/0315-0860(75)90032-4
• Knobloch, Eberhard, From Gauss to Weierstrass: determinant theory and its historical evaluations, The intersection of history and mathematics, Science Networks Historical Studies 15, Basel, Boston, Berlin: Birkhäuser: 51–66, 1994, MR 1308079
• Kronecker, Leopold, Hensel, Kurt , 編, Leopold Kronecker's Werke, Teubner, 1897
• Mehra, Jagdish; Rechenberg, Helmut, The Historical Development of Quantum Theory 1st, Berlin, DE; New York, NY: Springer-Verlag, 1987, ISBN 978-0-387-96284-9
• Shen, Kangshen; Crossley, John N.; Lun, Anthony Wah-Cheung, Nine Chapters of the Mathematical Art, Companion and Commentary 2nd, Oxford University Press, 1999, ISBN 978-0-19-853936-0
• Weierstrass, Karl, Collected works 3, 1915 [2012-05-06], （原始內容存檔於2008-10-11）

外部連結

百科全書

• Hazewinkel, Michiel (編), Matrix, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4

歷史

• MacTutor: Matrices and determinants （頁面存檔備份，存於互聯網檔案館）
• Matrices and Linear Algebra on the Earliest Uses Pages （頁面存檔備份，存於互聯網檔案館）
• Earliest Uses of Symbols for Matrices and Vectors （頁面存檔備份，存於互聯網檔案館）

線上書籍

• Kaw, Autar K., Introduction to Matrix Algebra, [2015-01-10], ISBN 978-0-615-25126-4, （原始內容存檔於2008-08-08）
• The Matrix Cookbook (PDF), [2014-03-24], （原始內容存檔 (PDF)於2013-12-12）
• Brookes, Mike, The Matrix Reference Manual, London: Imperial College, 2005 [2008-12-10], （原始內容存檔於2021-03-22）

線上矩陣計數機

• Matrix Calculator (DotNumerics), [2015-01-10], （原始內容存檔於2014-09-04）
• Xiao, Gang, Matrix calculator, [2008-12-10], （原始內容存檔於2020-06-12）
• Online matrix calculator, [2008-12-10], （原始內容存檔於2008-12-12）
• Online matrix calculator (ZK framework), [2009-11-26], （原始內容存檔於2013-05-12）
• Oehlert, Gary W.; Bingham, Christopher, MacAnova, University of Minnesota, School of Statistics, [2008-12-10], （原始內容存檔於2021-03-22）, a freeware package for matrix algebra and statistics
• Online matrix calculator, [2009-12-14], （原始內容存檔於2021-04-27）
• Operation with matrices in R (determinant, track, inverse, adjoint, transpose) （頁面存檔備份，存於互聯網檔案館）