温尼尔多面体模型列表

这里列出所有由马格努斯·J·温尼尔（英语：Magnus J. Wenninger）分类的所有多面体及星形多面体模型。

帕雷托立体（正图形）W1到W5

索引	名称	图像	对偶名称	对偶图像	威佐夫记号（英语：Wythoff symbol）	顶点布局（英语：Vertex configuration） 施莱夫利符号	对称群	U#	K#	V	E	F	面的类别
1	正四面体		正四面体		3|2 3	{3,3}	Td	U01	K06	4	6	4	4{3}
2	正八面体		立方体		4|2 3	{3,4}	Oh	U05	K10	6	12	8	8{3}
3	立方体（正六面体）		正八面体		3|2 4	{4,3}	Oh	U06	K11	8	12	6	6{4}
4	正二十面体		正十二面体		5|2 3	{3,5}	Ih	U22	K27	12	30	20	20{3}
5	正十二面体		正二十面体		3|2 5	{5,3}	Ih	U23	K28	20	30	12	12{5}

阿基米德立体（半正多面体）W6到W18

索引	名称	图像	对偶名称	对偶图像	威佐夫记号（英语：Wythoff symbol）	顶点布局（英语：Vertex configuration） 顶点图	对称群	U#	K#	V	E	F	面的类别
6	截角四面体		三角化四面体		2 3|3	3.6.6	Td	U02	K07	12	18	8	4{3} + 4{6}
7	截角八面体		四角化立方体		2 4|3	4.6.6	Oh	U08	K13	24	36	24	6{4} + 8{6}
8	截角立方体		三角化八面体		2 3|4	3.8.8	Oh	U09	K14	24	36	14	8{3} + 6{8}
9	截角二十面体		五角化十二面体		2 5|3	5.6.6	Ih	U25	K30	60	90	32	12{5} + 20{6}
10	截角十二面体		三角化二十面体		2 3|5	3.10.10	Ih	U26	K31	60	90	32	20{3} + 12{10}
11	截半立方体		菱形十二面体		2|3 4	3.4.3.4	Oh	U07	K12	12	24	14	8{3} + 6{4}
12	截半二十面体		菱形三十面体		2|3 5	3.5.3.5	Ih	U24	K29	30	60	32	20{3} + 12{5}
13	小斜方截半立方体		筝形二十四面体		3 4|2	3.4.4.4	Oh	U10	K15	24	48	26	8{3}+（6+12）{4}
14	小斜方截半二十面体		筝形六十面体		3 5|2	3.4.5.4	Ih	U27	K32	60	120	62	20{3} + 30{4} + 12{5}
15	大斜方截半立方体 （截角截半立方体）		四角化菱形十二面体		2 3 4|	4.6.8	Oh	U11	K16	48	72	26	12{4} + 8{6} + 6{8}
16	大斜方截半二十面体 （截角截半二十面体）		四角化菱形三十面体		2 3 5|	4.6.10	Ih	U28	K33	120	180	62	30{4} + 20{6} + 12{10}
17	扭棱立方体		五角二十四面体		|2 3 4	3.3.3.3.4	O	U12	K17	24	60	38	（8 + 24）{3} + 6{4}
18	扭棱十二面体		五角六十面体		|2 3 5	3.3.3.3.5	I	U29	K34	60	150	92	（20 + 60）{3} + 12{5}

星形正多面体W20、W21、W22和W41

索引	名称	图像	对偶名称	对偶图像	威佐夫记号（英语：Wythoff symbol）	顶点布局（英语：Vertex configuration） 施莱夫利符号	对称群	U#	K#	V	E	F	面的类别
20	小星形十二面体		大十二面体		5|25/2	{5/2,5}	Ih	U34	K39	12	30	12	12{5/2}
21	大十二面体		小星形十二面体		5/2|2 5	{5,5/2}	Ih	U35	K40	12	30	12	12{5}
22	大星形十二面体		大二十面体		3|25/2	{5/2,3}	Ih	U52	K57	20	30	12	12{5/2}
41	大二十面体		大星形十二面体		5/2|2 3	{3,5/2}	Ih	U53	K58	12	30	20	20{3}

星形：W19到W66

与八面体相关的星形

索引	名称	对称群	图像	星状图
2	正八面体	Oh
19	星形八面体 （二复合正四面体）	Oh

与十二面体相关的星形

索引	名称	对称群	图像	星状图
5	正十二面体（正图形）	Ih
20	小星形十二面体（正图形） （第一种星形十二面体）	Ih
21	大十二面体（正图形） （第二种星形十二面体）	Ih
22	大星形十二面体（正图形） （第三种星形十二面体）	Ih

与二十面体相关的星形

索引	名称	对称群	图像	星状图
4	正二十面体（正图形）	Ih
23	五复合正八面体 （第一种复合星形二十面体）	Ih
24	五复合正四面体 （第二种复合星形二十面体）	I
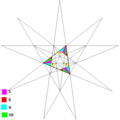
25	十复合正四面体 （第三种复合星形二十面体）	Ih
26	小三角六边形二十面体 （第一星形二十面体） （星形三角化二十面体）	Ih
27	第二星形二十面体	Ih
28	凹五角锥十二面体 （第三星形二十面体）	Ih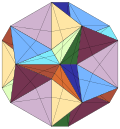
29	第四星形二十面体	Ih
30	第五星形二十面体	Ih
31	第六星形二十面体	Ih
32	第七星形二十面体（维基数据：Q108366673）	Ih
33	第八星形二十面体	Ih
34	第九星形二十面体 大三角六边形二十面体	Ih
35	第十星形二十面体（维基数据：Q108383813）	I
36	第十一星形二十面体（：The_Fifty-Nine_Icosahedra#Table_of_the_fifty-nine_icosahedra）	I
37	第十二星形二十面体（：The_Fifty-Nine_Icosahedra#Table_of_the_fifty-nine_icosahedra）	Ih
38	第十三星形二十面体（：The_Fifty-Nine_Icosahedra#Table_of_the_fifty-nine_icosahedra）	I
39	第十四星形二十面体	I
40	第十五星形二十面体（：The_Fifty-Nine_Icosahedra#Table_of_the_fifty-nine_icosahedra）	I
41	大二十面体（正图形） （第十六星形二十面体）	Ih
42	完全星形二十面体	Ih

星形截半立方体

索引	名称	对称群	图像	八面体星状图	立方体星状图
11	截半立方体 (原像)	Oh
43	复合八面体立方体 (第一种星形截半立方体)	Oh
44	第二种星形截半立方体	Oh
45	第三种星形截半立方体	Oh
46	第四种星形截半立方体	Oh

星形截半二十面体

索引	名称	对称群	图像	星状图 (二十面体面)	星状图 (十二面体面)
12	截半二十面体 (正)	Ih
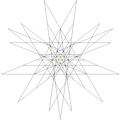
47	(第一种星形截半二十面体) 复合十二面体二十面体	Ih
48	第二种星形截半二十面体	Ih
49	第三种星形截半二十面体	Ih
50	第四种星形截半二十面体 (复合小星形十二 面体三角化二十面体)	Ih
51	第五种星形截半二十面体 (五复合正八面体小 星形十二面体)	Ih
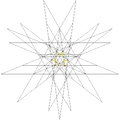
52	第六种星形截半二十面体	Ih
53	第七种星形截半二十面体	Ih
54	第八种星形截半二十面体 (五复合正八面 体小大十二面体)	I
55	第九种星形截半二十面体	Ih
56	第十种星形截半二十面体	Ih
57	第十一种星形截半二十面体	Ih
58	第十二种星形截半二十面体	Ih
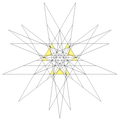
59	第十三种星形截半二十面体	Ih
60	第十四种星形截半二十面体	Ih
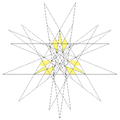
61	复合大二十面体大星形十二面体（英语：Compound of great icosahedron and great stellated dodecahedron）	Ih
62	第十五种星形截半二十面体	Ih
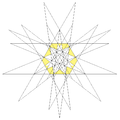
63	第十六种星形截半二十面体	Ih
64	第十七种星形截半二十面体	Ih
65	第十八种星形截半二十面体	Ih
66	第十九种星形截半二十面体	Ih

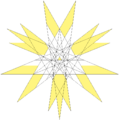
均匀非凸多面体W67到W119

编号	名称	图像	对偶	对偶图像	威佐夫记号（英语：Wythoff symbol）	顶点图	对称群	U#	K#	V	E	F	面的种类
67	四面半六面体		四面半无穷星形六面体		3/23|2	4.3/2.4.3	Td	U04	K09	6	12	7	4{3}+3{4}
68	八面半八面体		八面半无穷星形八面体		3/23|3	6.3/2.6.3	Oh	U03	K08	12	24	12	8{3}+4{6}
69	小立方立方八面体		小六角星化二十四面体（英语：Small hexacronic icositetrahedron）		3/24|4	8.3/2.8.4	Oh	U13	K18	24	48	20	8{3}+6{4}+6{8}
70	小双三斜三十二面体		小三角六边形二十面体		3|5/23	(5/2.3)3	Ih	U30	K35	20	60	32	20{3}+12{5/2}
71	小二十面化截半二十面体		小二十角星化六十面体（英语：Small icosacronic hexecontahedron）		5/23|3	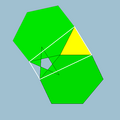6.5/2.6.3	Ih	U31	K36	60	120	52	20{3}+12{5/2}+20{6}
72	小十二面截半二十面体		小十二角星化六十面体（英语：Small dodecacronic hexecontahedron）		3/25|5	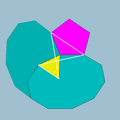10.3/2.10.5	Ih	U33	K38	60	120	44	20{3}+12{5}+12{10}
73	截半大十二面体		内侧菱形三十面体		2|5/25	(5/2.5)2	Ih	U36	K41	30	60	24	12{5}+12{5/2}
74	小斜方十二面体		小星形菱形十二面体（英语：Small rhombidodecacron）		25/25|	10.4.10/9.4/3	Ih	U39	K44	60	120	42	30{4}+12{10}
75	截角大十二面体		小星形五角化十二面体		25/2|5	10.10.5/2	Ih	U37	K42	60	90	24	12{5/2}+12{10}
76	斜方截半大十二面体		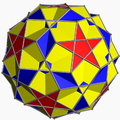中凧形六十面体（英语：Medial deltoidal hexecontahedron）		5/25|2	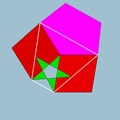4.5/2.4.5	Ih	U38	K43	60	120	54	30{4}+12{5}+12{5/2}
77	大立方截半立方体		大六角星化二十四面体		3 4|4/3	8/3.3.8/3.4	Oh	U14	K19	24	48	20	8{3}+6{4}+6{8/3}
78	立方半八面体		立方半无穷星形八面体		4/34|3	6.4/3.6.4	Oh	U15	K20	12	24	10	6{4}+4{6}
79	立方截角立方八面体		四重二方六面体（英语：Tetradyakis hexahedron）		4/33 4|	8/3.6.8	Oh	U16	K21	48	72	20	8{6}+6{8}+6{8/3}
80	双三斜十二面体		内侧三角六边形二十面体		3|5/35	(5/3.5)3	Ih	U41	K46	20	60	24	12{5}+12{5/2
81	大双三角十二面截半二十面体		大双三角十二角星化六十面体（英语：Great ditrigonal dodecacronic hexecontahedron）		3 5|5/3	10/3.3.10/3.5	Ih	U42	K47	60	120	44	20{3}+12{5}+12{10/3}
82	小双三角十二面截半二十面体		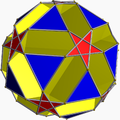小双三角十二角星化六十面体（英语：Small ditrigonal dodecacronic hexecontahedron）		5/33|5	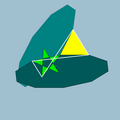10.5/3.10.3	Ih	U43	K48	60	120	44	20{3}+12{5/2}+12{10}
83	二十面化截半大十二面体		内侧二十角星化六十面体（英语：Medial icosacronic hexecontahedron）		5/35|3	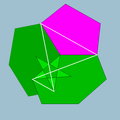6.5/3.6.5	Ih	U44	K49	60	120	44	12{5}+12{5/2}+20{6}
84	二十面截角十二面十二面体		三重二方二十面体（英语：Tridyakis icosahedron）		5/33 5|	10/3.6.10	Ih	U45	K50	120	180	44	20{6}+12{10}+12{10/3}
85	非凸大斜方截半立方体		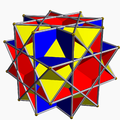大凧形二十四面体（英语：Great deltoidal icositetrahedron）		3/24|2	4.3/2.4.4	Oh	U17	K22	24	48	26	8{3}+(6+12){4}
86	小斜方立方体		小反平行四边形二十四面体		3/22 4|	4.8.4/3.8	Oh	U18	K23	24	48	18	12{4}+6{8}
87	大双三斜三十二面体		大三角六边形二十面体		3/2|3 5	(5.3.5.3.5.3)/2	Ih	U47	K52	20	60	32	20{3}+12{5}
88	大二十面化截半二十面体		大二十角星化六十面体（英语：Great icosacronic hexecontahedron）		3/25|3	6.3/2.6.5	Ih	U48	K53	60	120	52	20{3}+12{5}+20{6}
89	小二十面半十二面体		小二十面半无穷星形十二面体（英语：Small icosihemidodecacron）		3/23|5	10.3/2.10.3	Ih	U49	K54	30	60	26	20{3}+6{10}
90	小十二面二十面体		小十二面二十面六十面体（英语：Small dodecicosacron）		3/23 5|	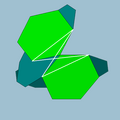10.6.10/9.6/5	Ih	U50	K55	60	120	32	20{6}+12{10}
91	小十二面半十二面体		小十二面半无穷星形十二面体（英语：Small dodecahemidodecacron）		5/45|5	10.5/4.10.5	Ih	U51	K56	30	60	18	12{5}+6{10}
92	星形截角立方体		大三角化八面体		2 3|4/3	8/3.8/3.3	Oh	U19	K24	24	36	14	8{3}+6{8/3}
93	星形截角截半立方体		大六角化八面体（英语：Great disdyakis dodecahedron）		4/32 3|	8/3.4.6	Oh	U20	K25	48	72	26	12{4}+8{6}+6{8/3}
94	大截半二十面体		大菱形三十面体		2|5/23	(5/2.3)2	Ih	U54	K59	30	60	32	20{3}+12{5/2}
95	截角大二十面体		大星形五角化十二面体		25/2|3	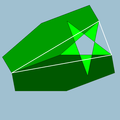6.6.5/2	Ih	U55	K60	60	90	32	12{5/2}+20{6}
96	斜方二十面体		斜方星形二十面体		25/23|	6.4.6/5.4/3	Ih	U56	K61	60	120	50	30{4}+20{6}
97	小星形截角十二面体		大五方十二面体（英语：Great pentakis dodecahedron）		2 5|5/3	10/3.10/3.5	Ih	U58	K63	60	90	24	12{5}+12{10/3}
98	截角截半大十二面体		内侧双二方三十面体（英语：Medial disdyakis triacontahedron）		5/32 5|	10/3.4.10	Ih	U59	K64	120	180	54	30{4}+12{10}+12{10/3}
99	大十二面截半二十面体		大十二角星化六十面体（英语：Great dodecacronic hexecontahedron）		5/23|5/3	10/3.5/2.10/3.3	Ih	U61	K66	60	120	44	20{3}+12{5/2}+12{10/3 }
100	小十二面半二十面体		小十二面半无穷星形二十面体（英语：Small dodecahemicosacron）		5/35/2|3	6.5/3.6.5/2	Ih	U62	K67	30	60	22	12{5/2}+10{6}
101	大十二面二十面体		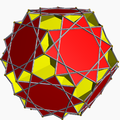大十二面二十面六十面体		5/35/23|	6.10/3.6/5.10/7	Ih	U63	K68	60	120	32	20{6}+12{10/3}
102	大十二面半二十面体		大十二面半无穷星形二十面体（英语：Great dodecahemicosacron）		5/45|3	6.5/4.6.5	Ih	U65	K70	30	60	22	12{5}+10{6}
103	大斜方立方体		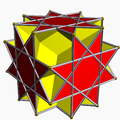反平行四边形二十四面体		4/33/22|	4.8/3.4/3.8/5	Oh	U21	K26	24	48	18	12{4}+6{8/3}
104	大星形截角十二面体		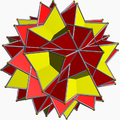大三角化二十面体（英语：Great_triakis_icosahedron）		2 3|5/3	10/3.10/3.3	Ih	U66	K71	60	90	32	20{3}+12{10/3}
105	非凸大斜方截半二十面体		大凧形六十面体（英语：Great deltoidal hexecontahedron）		5/33|2	4.5/3.4.3	Ih	U67	K72	60	120	62	20{3}+30{4}+12{5/2}
106	大二十面半十二面体		大二十面半无穷星形十二面体（英语：Great icosihemidodecacron）		3 3|5/3	10/3.3/2.10/3.3	Ih	U71	K76	30	60	26	20{3}+6{10/3}
107	大十二面半十二面体		大十二面半无穷星形十二面体（英语：Great dodecahemidodecacron）		5/35/2|5/3	10/3.5/3.10/3.5/2	Ih	U70	K75	30	60	18	12{5/2}+6{10/3}
108	大截角截半二十面体 （星形截角截半二十面体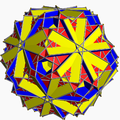）		大四角化菱形三十面体（维基数据：Q18048490）		5/32 3|	10/3.4.6	Ih	U68	K73	120	180	62	30{4}+20{6}+12{10/3}
109	大斜方十二面体		大菱形十二面六十面体（英语：Great rhombidodecacron）		3/25/32|	4.10/3.4/3.10/7	Ih	U73	K78	60	120	42	30{4}+12{10/3}
110	完全扭棱二十面体		小六角六十面体（英语：Small hexagonal hexecontahedron）		|5/23 3	3.3.3.3.3.5/2	Ih	U32	K37	60	180	112	(40+60){3}+12{5/2}
111	扭棱小星形十二面体		中五角六十面体（英语：Medial pentagonal hexecontahedron）		|25/25	3.3.5/2.3.5	I	U40	K45	60	150	84	60{3}+12{5}+12{5/2}
112	扭棱二十面化截半大十二面体		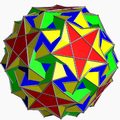中六角六十面体（英语：Medial hexagonal hexecontahedron）		|5/33 5	3.3.3.3.5.5/3	I	U46	K51	60	180	104	(20+6){3}+12{5}+12{5/2}
113	反扭棱大星形十二面体		大逆五角六十面体（维基数据：Q18048506）		|5/32 3	3.3.3.3.5/3	I	U69	K74	60	150	92	(20+60){3}+12{5/2}
114	反扭棱小星形十二面体		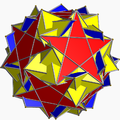中逆五角六十面体（英语：Medial inverted pentagonal hexecontahedron）		|5/32 5	3.5/3.3.3.5	I	U60	K65	60	150	84	60{3}+12{5}+12{5/2}
115	大扭棱十二面截半二十面体		大六角六十面体（英语：Great hexagonal hexecontahedron）		|5/35/23	3.5/3.3.5/2.3.3	I	U64	K69	60	180	104	(20+60){3}+(12+12){5/2}
116	扭棱大星形十二面体		大五角六十面体（英语：Great pentagonal hexecontahedron）		|25/25/2	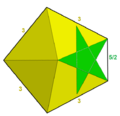3.3.3.3.5/2	I	U57	K62	60	150	92	(20+60){3}+12{5/2}
117	大反屈扭棱截半二十面体		大五角星六十面体（英语：Great pentagrammic hexecontahedron）		|3/25/32	(3.3.3.3.5/2)/2	I	U74	K79	60	150	92	(20+60){3}+12{5/2}
118	小反屈扭棱二十面截半二十面体		小六角星六十面体（英语：Small hexagrammic hexecontahedron）		|3/23/25/2	(3.3.3.3.3.5/2)/2	Ih	U72	K77	180	60	112	(40+60){3}+12{5/2}
119	大二重斜方截半二十面体		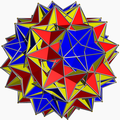大二重斜方截半二十面无穷星形六十面体（英语：Great dirhombicosidodecacron）		|3/25/335/2	(4.5/3.4.3.4.5/2.4.3/2)/2	Ih	U75	K80	60	240	124	40{3}+60{4}+24{5/2}

参见

• 均匀多面体列表（英语：List of uniform polyhedra）
• 五十九种二十面体

参考文献

• Wenninger, Magnus（英语：Magnus J. Wenninger）. Polyhedron Models. Cambridge University Press. 1974. ISBN 0-521-09859-9.
  • Errata
    • In Wenninger, the vertex figure for W90 is incorrectly shown as having parallel edges.
• Wenninger, Magnus（英语：Magnus J. Wenninger）. Spherical Models. Cambridge University Press. 1979. ISBN 0-521-29432-0.

外部链接

• Magnus J. Wenninger
• Software used to generate images in this article:
  • Stella: Polyhedron Navigator （页面存档备份，存于互联网档案馆） Stella （software） - Can create and print nets for all of Wenninger's polyhedron models.
  • Vladimir Bulatov's Polyhedra Stellations Applet （页面存档备份，存于互联网档案馆）
  • Vladimir Bulatov's Polyhedra Stellations Applet packaged as an OS X application （页面存档备份，存于互联网档案馆）
• M. Wenninger, Polyhedron Models, Errata （页面存档备份，存于互联网档案馆）: known errors in the various editions.