四角化立方体

在几何学中，四角化立方体又称为四角化六面体是一种卡塔兰立体，其对偶多面体为截角正八面体，由24个全等的等腰三角形组成，具有36条边和14个顶点^[1]，可以视为在正方体的每个面上加入正四角锥的结果。此外四角化立方体亦可以视为正方形四边各加一个等腰三角形拼成的正八边形在立体几何中的推广。

四角化立方体

（按这里观看旋转模型）
类别	卡塔兰立体
对偶多面体	截角正八面体
识别
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	tekah
数学表示法
考克斯特符号 （英语：Coxeter-Dynkin diagram）
康威表示法	kC dtO
性质
面	24
边	36
顶点	14
欧拉特征数	F=24, E=36, V=14 （χ=2）
二面角	143°07′48″ ${\displaystyle \arccos(-{\frac {4}{5}})}$
组成与布局
面的种类	V4.6.6 等腰三角形
面的布局 （英语：Face configuration）	6{4}+8{6}
顶点图	V4.6.6
对称性
对称群	Oh, B3, [4,3], (*432)
旋转对称群 （英语：Rotation_groups）	O, [4,3]+, (432)
特性
凸、面可递
图像
V4.6.6 （顶点图） 截角正八面体 （对偶多面体） （展开图）
查 论 编

性质

四角化立方体是一个卡塔兰立体^[2]，由24个面、36条边和14个顶点组成^[1]，其中24面为24个全等的等腰三角形，是一种二十四面体，其对偶多面体为截角八面体^[3][4]。在四角化立方体的14个顶点中，有6个顶点是4个等腰三角形的公共顶点，对应的顶角是四面角；另外8个顶点是6个等腰三角形的公共顶点，对应的顶角是六面角^[5][6]。

此外四角化立方体可以视为在正方体的每个面上加入适当锥高的正四角锥的结果^[7]，其加入的正四角锥锥高不能高过原本的正方体表面到其外接球的距离，为四分之一倍的立方体边长^[8]，若超过则会变成菱形十二面体或星形的四角化立方体。

此外，立方体、八面体和星形八面体都可以以顶点共用的方式，内接在四角化立方体内^[8]。

体积与表面积

若四角化立方体的最短的边长为a，则其表面积A及体积V为^[8]：

表面积${\displaystyle A=a^{2}\times {\frac {16{\sqrt {5}}}{3}}\approx a^{2}\times 11.9257}$

体积为${\displaystyle V=a^{3}\times {\frac {32}{9}}\approx a^{3}\times 3.5556}$。

若其对偶多面体的截角正八面体边长为a，则对应的四角化立方体之体积V为^[5]：

体积为${\displaystyle V=a^{3}\times {\frac {81{\sqrt {2}}}{8}}\approx a^{3}\times 14.3189}$。

面的组成

四角化立方体由24个全等的等腰三角形组成^[9]。

组成四角化立方体的等腰三角形的2个底角为arccos${\displaystyle \scriptstyle {\left({\tfrac {2}{3}}\right)}}$约为48.19°^[10]，由三角形内角关系可知顶角约为83.62°^[11][10]，边长比为1:1:${\displaystyle {\begin{matrix}{\frac {4}{3}}\end{matrix}}}$^[12][10]。

顶点坐标

若一个四角化立方体对应的对偶多面体边长为单位长（对应的四角化立方体最短边长为${\displaystyle {\tfrac {9{\sqrt {2}}}{8}}}$单位）且几何中心位于原点，则其顶点坐标为^[13]：

${\displaystyle \left(0\,,\quad 0\,,\quad \pm {\frac {9{\sqrt {2}}}{8}}\right)}$

${\displaystyle \left(\pm {\frac {9{\sqrt {2}}}{8}}\,,\quad 0\,,\quad 0\right)}$

${\displaystyle \left(0\,,\quad \pm {\frac {9{\sqrt {2}}}{8}}\,,\quad 0\right)}$

${\displaystyle \left(\pm {\frac {3{\sqrt {2}}}{4}}\,,\quad \pm {\frac {3{\sqrt {2}}}{4}}\,,\quad \pm {\frac {3{\sqrt {2}}}{4}}\right)}$

对称性

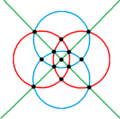
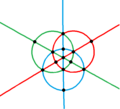
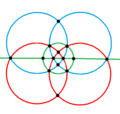
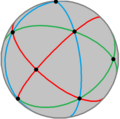
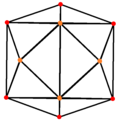
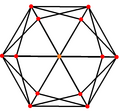
四角化立方体具有T_d, [3,3] (*332)的四面体群对称性（英语：tetrahedral symmetry），其24个等腰三角形代表四面体对称的24个基本域。 在球面上，四角化立方体可以透过6个球面大圆来构建。相同的结构也可以透过将立方体在每个正方形面上以正方形的几何中心为基准将正方形分成四个三角形^[14]、或透过将正四面体在每个三角形面上以正三角形的顶点、边中点和几何中心为基准将正三角形分成6个三角形来看出。

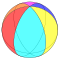
四角化立方体可以投影到球面上，形成球面多面体^[15]。在球极平面投影中，四角化立方体的棱可以在平面上形成6个圆或中心径向线，每个圆或中心径向线皆代表四面体群对称性的镜射线。这6个圆可以分成3组每两两一对的正交圆，这三组正交圆，每组在球面上皆可以视为1个正四面形。

球极平面投影			透视投影		施莱格尔投影（英语：Schlegel diagram）
[4]	[3]	[2]	歪斜

正交投影

四角化立方体有三种高对称性的正交投影，分别为两种在顶点上的正交投影以及一种在棱上中点的正交投影。 后两者的对偶图其对称性对应于B₂和A₂的考克斯特平面（英语：Coxeter plane）^[16][17]。

正交投影

投影对称性	[2]	[4]	[6]
四角化立方体
截角八面体

使用

四角化立方体骰子

在矿物学中，这种形状又称为四六面体^[18]（英语：tetrahexahedron^[19][20]），部分的矿石可以结晶成这种形状^[21][22]，例如部分的钙铁榴石^[23]，以及能在部分的铜和氟的结晶系统中被观测到。

此外，亦有部分24个面的多面体骰子被设计为四角化立方体的外型^[24]。

相关多面体与镶嵌

四角化立方体可以经由八面体的对偶多面体——立方体透过四角化变换构造，即将立方体每个面贴上正四角锥来获得^[7]。其他也是由正八面体或其对偶多面体透过康威变换得到的多面体有：

半正正八面体家族多面体

对称性: [4,3], (*432)							[4,3]+, (432)	[1+,4,3], (*332)	[4,3+], (3*2)
{4,3}	t0,1{4,3}	t1{4,3}	t1,2{4,3}	{3,4}	t0,2{4,3}	t0,1,2{4,3}	s{4,3}	h{4,3}	h1,2{4,3}
半正多面体的对偶
V4.4.4	V3.8.8	V3.4.3.4	V4.6.6	V3.3.3.3	V3.4.4.4	V4.6.8	V3.3.3.3.4	V3.3.3	V3.3.3.3.3

四角化立方体是由等腰三角形组成^[10]，且对偶多面体由正方形与正六边形组成。同样由等腰三角形组成，且对偶多面体由正多边形与正六边形组成的多面体或镶嵌图包括：

*n32变异对称性 n.6.6 的截角镶嵌：
对称性 *n42 [n,3]	球面镶嵌（英语：List_of_spherical_symmetry_groups）				欧氏镶嵌（英语：List_of_planar_symmetry_groups）	紧凑双曲		仿紧双曲	非紧双曲
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
截角镶嵌
顶点（英语：Vertex configuration）	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n角化 镶嵌
面（英语：Face configuration）	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

对偶复合体

四角化立方体的对偶复合体，为四角化立方体和截角八面体组合成的复合图形，称为复合截角八面体四角化立方体。其共有38个面、72条边和38个顶点，其尤拉示性数为4，亏格为-1^[25]。

四角化立方体图

四角化立方体图
度分布	4 (6个) 6 (8个)
顶点	14
边	36
半径	3[26]
直径	3[26]
围长	3
色数	3[26]
色指数	6
对偶图	截角八面体图（英语：Truncated octahedral graph）
属性	平面, 可积（英语：Integral graph）
查 论 编

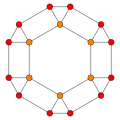
在图论的数学领域中，与四角化立方体相关的图为四角化立方体图（Disdyakis Dodecahedral Graph），是四角化立方体之边与顶点的图（英语：1-skeleton）^[26]，是一个阿基米德对偶图^[27]。

性质

四角化立方体图有36条边和14个顶点，其中度为4的顶点有6个、度为6的顶点有8个。^[26]

其特征多项式为^[26]：

${\displaystyle x^{2}{\left(x+1\right)}^{3}{\left(x+3\right)}{\left(x^{2}-3x-12\right)}{\left(x^{2}-x-4\right)}^{3}}$

参见

• 四角化菱形三十面体
• 四角化菱形十二面体
• 四角化菱形镶嵌——四角化的菱形镶嵌
• 三复合正八面体
• 筝形二十四面体——另外一个卡塔兰二十四面体

参考文献

1. Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
2. Wenninger, Magnus, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 0730208, doi:10.1017/CBO9780511569371 (The thirteen semiregular convex polyhedra and their duals, Page 14, Tetrakishexahedron)
3. The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Tetrakis hexahedron)

1. Tetrakis Hexahedron. Honeylocust Media Systems, polyhedra.org. 2006 [2008-08-28]. （原始内容存档于2008-08-28）.
2. Koca, Mehmet and Koca, Nazife Ozdes and Koc, Ramazan. Affine coxeter group Wa (A4), quaternions, and decagonal quasicrystals. International Journal of Geometric Methods in Modern Physics (World Scientific). 2014, 11 (04): 1450031.
3. Eric W. Weisstein. Tetrakis Hexahedron. 密歇根州立大学. 1999-05-26 [2019-09-01]. （原始内容存档于2013-06-21）.
4. Holden, A. Shapes, Space, and Symmetry (Dover Books on Mathematics). Dover Publications. 1971: p. 55. 引文格式1维护：冗余文本 (link)
5. Catalan Solids: Tetrakis Hexahedron. dmccooey.com. [2019-09-01]. （原始内容存档于2018-05-01）.
6. Eugène Catalan. Mémoire sur la Théorie des Polyèdres. Journal de l'École polytechnique. 1865, 41: pp.1–71, +7 plates. 引文格式1维护：冗余文本 (link)
7. Ruhnow, M. Duality in simple single atomic type crystal structures. Crystal Research and Technology (Wiley Online Library). 2012, 47 (4): 369––376.
8. Weisstein, Eric W. (编). Tetrakis Hexahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
9. Ugo Adriano Graziotti, PLATE 3: Solid Tetrakis Hexahedron, Polyhedra: The Realm of Geometric Beauty, U. A. G., University of San Francisco, 1962 [2019-09-05], （原始内容存档于2021-08-23）
10. Tetrakis hexahedron. fillygons.ch. [2019-09-03]. （原始内容存档于2019-09-01）.
11. Pugh, A. Polyhedra: A Visual Approach. The Dome series. University of California Press: 43. 1976 [2019-09-03]. ISBN 9780520030565. LCCN 74027297. （原始内容存档于2019-06-29）.
12. Weisstein, E.W. CRC Concise Encyclopedia of Mathematics, Second Edition. CRC Press. 2002: 2732-2733. ISBN 9781420035223.^{[失效链接]}
13. Data of Tetrakis Hexahedron. dmccooey.com. [2019-09-01]. （原始内容存档于2018-01-24）.
14. W. von Kühnel, Minimal triangulations of Kummer varieties, Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 57 (1) (Springer), 1987, 57 (1): 7
15. Rodrigues, Fernando Alves and Temporão, Guilherme and von der Weid, Jean Pierre. Constructive Methods for the Design and Labeling of Four-Dimensional Modulations. Journal of Communication and Information Systems. 2018, 33 (1).
16. 约翰·史坦布里奇（英语：John Stembridge）. Coxeter Planes. math.lsa.umich.edu. [2019-09-05]. （原始内容存档于2018-02-10）.
17. 约翰·史坦布里奇（英语：John Stembridge）. More Coxeter Planes. math.lsa.umich.edu. [2019-09-05]. （原始内容存档于2017-08-21）.
18. 四六面體 tetrakishexahedron (tetrahexahedron). 国家教育研究院. [2019-09-01]. （原始内容存档于2019-09-01）.
19. Correns, C. W. Einführung in die Mineralogie (Kristallographie und Petrologie). Berlin: Springer-Verlag. 1949: p. 41. 引文格式1维护：冗余文本 (link)
20. Berry, L. G. and Mason, B. Mineralogy: Concepts, Descriptions, Determinations. San Francisco, CA: W. H. Freeman, 1959., p. 127
21. 中川宏. 貫入双晶模型の製作 (PDF). [2019-09-01]. （原始内容存档 (PDF)于2019-09-01）.
22. Tappert, R. and Tappert, M.C. Diamonds in Nature: A Guide to Rough Diamonds. Springer Berlin Heidelberg. 2011: p.26. ISBN 9783642125720. LCCN 2011924333. 引文格式1维护：冗余文本 (link)
23. 高田雅介 著. 日本産鉱物の結晶形態 : 高田鉱物標本・結晶図集. 今井裕之. 2010年4月 （日语）.
24. Kybos, Alea. Properties of Dice (PDF). [7 October 2012]. （原始内容 (PDF)存档于2012-05-28）.
25. compound of truncated octahedron and tetrakishexahedron. bulatov.org. [2019-09-06]. （原始内容存档于2017-12-06）.
26. Weisstein, Eric W. (编). Tetrakis Hexahedral Graph. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
27. Weisstein, Eric W. (编). Archimedean Dual Graph. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.

外部链接

• 埃里克·韦斯坦因, 四角化立方体 （参阅卡塔兰立体） 于MathWorld（英文）
• Virtual Reality Polyhedra（页面存档备份，存于互联网档案馆） www.georgehart.com: The Encyclopedia of Polyhedra
  • VRML model （页面存档备份，存于互联网档案馆）
  • Conway Notation for Polyhedra（页面存档备份，存于互联网档案馆） Try: "dtO" or "kC"
• Tetrakis Hexahedron – Interactive Polyhedron model
• The Uniform Polyhedra（页面存档备份，存于互联网档案馆）