Сложение

Символы со сходным начертанием: Σ · Ʃ · 𐌔 · ᛊ

Сложе́ние (прибавле́ние^[2]) — одна из основных бинарных математических операций (арифметических действий) двух аргументов (слагаемых), результатом которой является новое число (сумма), получаемое увеличением значения первого аргумента на значение второго аргумента. То есть каждой паре элементов ${\displaystyle (a,b)}$ из множества ${\displaystyle A}$ ставится в соответствие элемент ${\displaystyle c=a+b}$, называемый суммой ${\displaystyle a}$ и ${\displaystyle b}$.

В учебниках часто объясняют сложение с помощью яблок и равенства 3 + 2 = 5^[1]

Обратная операция к сложению — вычитание^[3].

Это одна из четырёх элементарных^[англ.] математических операций арифметики. Приоритет её в обычном порядке операций равен приоритету вычитания, но ниже, чем у возведения в степень, извлечения корня, умножения и деления^[4]. На письме сложение обычно обозначается с помощью знака «плюс»: ${\displaystyle a+b=c}$, то есть аддитивной записью.

У сложения есть несколько важных свойств (например, для ${\displaystyle A=}$${\displaystyle \mathbb {R} }$) (см. Сумма):

• Коммутативность: ${\displaystyle a+b=b+a,\quad \forall a,b\in \ A;}$➤
• Ассоциативность: ${\displaystyle (a+b)+c=a+(b+c),\quad \forall a,b,c\in \ A;}$➤
• Дистрибутивность: ${\displaystyle x\cdot (a+b)=(x\cdot a)+(x\cdot b)}$ и ${\displaystyle (a+b)\cdot x=(a\cdot x)+(b\cdot x),\quad \forall a,b\in \ A;}$
• Прибавление ${\displaystyle 0}$ (нулевого элемента) даёт число, равное исходному: ${\displaystyle x+0=0+x=x,\quad \forall x\in A,\quad \exists 0\in A.}$

Используя систематические обобщения, сложение можно определить для абстрактных величин, таких как целые числа, рациональные числа, вещественные числа и комплексные числа и для других абстрактных объектов, таких как векторы и матрицы.

Сложение возможно, только если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип). Так, на картинке справа запись ${\displaystyle 3+2}$ обозначает три яблока и два яблока вместе, что в сумме даёт пять яблок. Но нельзя сложить, например, 3 яблока и 2 груши.

Как правило, сложение не используется для наименования операций, которые не подчиняются коммутативному и ассоциативному законам^[5][6].

В теории групп обычно сложением называют операцию в абелевой группе (при аддитивной записи) и ту бинарную операцию в кольце, относительно которой элементы кольца образуют абелеву группу, где сложение ассоциативно и коммутативно. Иногда сложением называется и некоммутативная групповая операция, например, операция в мулътиоператорной группе^[3].

Сложение небольших чисел является одним из первых навыков, прививаемых детям в начальной школе.

Известны различные устройства для сложения: от древних абаков и классических русских счётов до современных компьютеров и калькуляторов.

Формы записи и терминология

Символ плюса

Сложение записывается с использованием символа плюса «+» между слагаемыми; такая форма записи называется инфиксной нотацией. Результат записывается с использованием знака равенства. Например,

• ${\displaystyle a+b=c}$ («а плюс бэ равно цэ»)
• ${\displaystyle 1+1=2}$ («один плюс один равно двум»)
• ${\displaystyle 2+2=4}$ («два плюс два равно четырём»)
• ${\displaystyle 5+4+2=11}$ (см. «ассоциативность» ниже)
• ${\displaystyle 3+3+3+3=12}$ (см. «умножение» ниже)

Сложение в столбик:
5 + 12 = 17

В ряде ситуаций подразумевается сложение, но при этом символы сложения не используются:

• В записи чисел в позиционных системах счисления: запись числа ${\displaystyle a_{n-1}\;a_{n-2}\ldots \;a_{1}\;a_{0},}$ подразумевает суммирование ряда ${\displaystyle a_{n-1}\cdot P^{n-1}+a_{n-2}\cdot P^{n-2}+\ldots +a_{1}\cdot P^{1}+a_{0}\cdot P^{0}}$^[7].
• Если имеется столбец чисел, последнее (нижнее) число в котором подчёркнуто, то обычно подразумевается, что все числа в этом столбце складываются, а полученная сумма записывается ниже подчёркнутого числа.
• Если имеется запись, когда перед дробью стоит целое число, то эта запись означает сумму двух слагаемых — целого числа и дроби, которую называют смешанным числом^[8]. Например,
  3½ = 3 + ½ = 3.5.
  Такая запись может вызвать путаницу, поскольку в большинстве других случаев подобная запись означает умножение, а не сложение^[9].

Сумма ряда связанных чисел может быть записана с использованием символа Σ, который позволяет компактно записать итерацию. Например,

${\displaystyle \sum _{k=1}^{5}k^{2}=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}=55.}$

Слагаемые — это числа или объекты, складываемые друг с другом^[10].

Символ плюса «+» (Юникод:U+002B; ASCII: +) — упрощение латинского слова «et», означающего «и»^[11]. Впервые этот символ встречается в книгах, начиная с 1489 г.^[12]

Интерпретации

Сложение используется для моделирования бесчисленного множества физических процессов. Даже для простого сложения натуральных чисел существует много различных интерпретаций и ещё больше способов визуального представления.

Комбинирование наборов

Возможно, самая фундаментальная интерпретация сложения — комбинирование наборов:

• Если два или более не пересекающихся наборов объектов объединены в один набор, то число объектов в полученном наборе равно сумме числа объектов в исходных наборах.

Эту интерпретацию легко визуализировать, при этом опасность двусмысленности будет минимальной. Однако непонятно, как с помощью этой интерпретации сложения объяснить сложение дробных или отрицательных чисел^[13].

Одним из возможных решений будет обращение к набору объектов, которые могут быть легко разделены, например, пироги или стержни с сегментами^[14]. Вместо комбинирования наборов сегментов стержни могут быть присоединены друг к другу концами, что иллюстрирует другую концепцию сложения: складываются не стержни, складываются их длины.

Расширение длины

Визуализация суммы 2 + 4 = 6 на числовой прямой. Сдвиг на 2 и затем сдвиг на 4 — это то же самое, что и сдвиг на 6.

Ещё один вариант визуализации суммы 2 + 4 = 6 на числовой прямой. Сдвиг на 4 — это то же самое, что и четыре сдвига по 1.

Вторая интерпретация сложения заключается в расширении начальной длины на величину добавляемой длины:

• Когда начальная длина расширяется добавляемой длиной, то полученная длина равна сумме начальной длины и длины, которую к ней добавили^[15].

Сумму a + b можно интерпретировать как бинарную операцию объединения a и b в алгебраическом смысле, также её можно интерпретировать как добавление b единиц к числу a. В последней интерпретации части суммы a + b играют асимметричные роли, и операция a + b рассматривается как применение к числу a унарной операции +b^[16]. Унарный подход позволяет перейти к вычитанию, ведь каждая унарная операция сложения имеет обратную унарную операцию вычитания и наоборот.

Свойства

Операция сложения на числовых множествах ${\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} }$ имеет следующие основные свойства:

Коммутативность

Визуализация 4 + 2 = 2 + 4 при помощи блоков

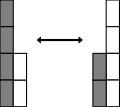
Сложение коммутативно — от перемены мест слагаемых сумма не меняется (это свойство также известно как переместительный закон сложения): ${\displaystyle a+b=b+a,\quad \forall a,b\in \ A.}$ Есть и другие законы коммутативности: например, существует коммутативный закон умножения. Тем не менее многие бинарные операции, например, вычитание и деление, не коммутативны.

Ассоциативность

Визуализация 2+(1+3) = (2+1)+3 при помощи стержней с сегментами

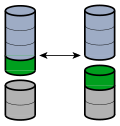
Сложение ассоциативно — при последовательном выполнении сложения трёх или более чисел последовательность выполнения операций не имеет значения (сочетательный закон сложения): ${\displaystyle (a+b)+c=a+(b+c),\quad \forall a,b,c\in \ A.}$

Дистрибутивность

Сложение дистрибутивно, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве (распределительный закон)^[17] : ${\displaystyle x\cdot (a+b)=(x\cdot a)+(x\cdot b),\quad \forall a,b\in \ A.}$

Нейтральный элемент

Визуализация 5 + 0 = 5 при помощи сумок с точками

Относительно сложения в множестве ${\displaystyle A}$ существует единственный нейтральный элемент, сложение числа с ${\displaystyle 0}$ (нулевым или нейтральным элементом) даёт число, равное исходному: ${\displaystyle x+0=0+x=x,\quad \forall x\in A,\quad \exists 0\in A.}$

Этот закон был впервые описан в Исправленном трактате Брахмы^[англ.], который был написан Брахмагуптой в 628 г. Он написал этот закон в виде трёх отдельных законов: для отрицательного, положительного и нулевого числа a, и для описания этих законов он использовал слова, а не алгебраические символы. Позже индийские математики уточнили понятия; около 840 г., Махавира^[англ.] написал, что «ноль становится таким же, как то, что добавляется к нему», что соответствовало записи 0 + a = a. В XII веке Бхаскара II написал: «Если добавить ничего или вычесть ничего, то количество, положительное или отрицательное, остаётся таким же, как и было», что соответствует записи a + 0 = a^[18].

Обратный элемент

Сложение с противоположным элементом даёт ${\displaystyle 0}$: ${\displaystyle a+(-a)=0,\quad \forall a\in A,\quad \exists -a\in A.}$^[19]

Кроме того, сложение не выводит результат за пределы данного множества чисел, следовательно, ${\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} }$ замкнуты относительно операции сложения. Эти множества с операциями ${\displaystyle +}$ и ${\displaystyle \cdot }$ образуют кольца (коммутативные кольца с единицей)^[20]. На языке общей алгебры вышеперечисленные свойства сложения говорят о том, что ${\displaystyle \mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} }$ — абелевы группы относительно операции сложения.

Выполнение сложения

Операцию сложения можно представить как некий «чёрный ящик» с двумя слагаемыми на входе и одним выходом - суммой:^[21][22]

При практическом решении задачи сложения двух чисел необходимо свести её к последовательности более простых операций: "простое сложение"^{[источник не указан 3023 дня]}, перенос, сравнение и др. Для этого разработаны различные методы сложения, например для чисел, дробей, векторов и др. На числовых множествах используется алгоритм поразрядного сложения^[23]. При этом следует рассматривать сложение как процедуру (в отличие от операции).

Примерный алгоритм процедуры поразрядного сложения двух чисел^[24]

Как видим, процедура достаточно сложная, состоит из относительно большого числа шагов и при сложении больших чисел может занять продолжительное время.

"Простое сложение" - в данном контексте обозначает операцию сложения одноразрядных чисел, которая может быть легко сведена к инкрементированию.^{[источник не указан 3023 дня]} является гипероператором инкрементирования:

Пример пошагового сложения чисел 2 и 4 на числовой прямой.

${\displaystyle a+b=\operatorname {hyper1} (a,b)=\operatorname {hyper} (a,1,b)=a^{(1)}b.}$

${\displaystyle a{^{(1)}}b=a+b=\underbrace {1+1+\dots +1} _{a}+\underbrace {1+1+\dots +1} _{b}.}$

где ${\displaystyle 1+1+\dots +1}$ - последовательность операций инкрементирования, выполненная ${\displaystyle a}$ и ${\displaystyle b}$ раз.

В худшем случае нахождение десятичной суммы двух десятичных одноразрядных чисел последовательным инкрементированием выполняется за 9 + 9 = 18 операций инкрементирования. В табличном десятичном полусумматоре нахождение десятичной суммы двух десятичных одноразрядных чисел выполняется за одну операцию чтения числа из массива чисел 10x10, т.е. быстрее, чем последовательным инкрементированием.

"Простое сложение" (одноразрядное двухоперандное (двухаргументное) десятичное сложение) является одной из ${\displaystyle 10^{200}}$ бинарных (двухаргументных, двухоперандных, двухвходовых) десятичных логических функций с бинарным (двухразрядным) результатом, имеющей кроме собственного номера и собственное название словами: "одноразрядный десятичный полусумматор".

Десятичной функцией в теории функциональных систем и в десятичной логике называют функцию типа ${\displaystyle {\mathsf {D}}^{n}\to {\mathsf {D}}}$, где ${\displaystyle {\mathsf {D}}=\{0,1,2,3,4,5,6,7,8,9\}}$ — десятичное множество, а ${\displaystyle \ n}$ — неотрицательное целое число, которое называют арностью или местностью функции.

Всего существует ${\displaystyle 10^{(10^{m})*n}=10^{(10^{2})*2}=10^{100*2}=10^{200}}$ простейших бинарных с бинарным (двухразрядным) результатом десятичных логических функций (2 децита -> 2 децита), где m - количество аргументов функции (входная "-арность"), а n - количество результатов действия функции (выходная "-арность"), что больше всех больших чисел Дирака вместе взятых и числа Шеннона (оценочное минимальное количество неповторяющихся шахматных партий, вычисленное в 1950 году американским математиком Клодом Шенноном, составляет приблизительно ${\displaystyle 10^{120}}$) впридачу.

Одноразрядное двухоперандное (двухаргументное) десятичное сложение можно также представить, как комбинацию (объединение двух) бинарных (двухаргументных, двухоперандных, двухвходовых) десятичных логических функцией с унарным (одноразрядным) результатом, имеющих кроме собственных номеров и собственные названия словами: "одноразрядное десятичное бинарное сложение по модулю 10" и "единица переноса в следующий разряд при одноразрядном десятичном бинарном сложении".

Всего существует ${\displaystyle 10^{(10^{2})}=10^{100}}$ простейших бинарных с унарным (одноразрядным) результатом десятичных логических функций (2 децита -> 1 децит).

Номер функции "одноразрядное десятичное бинарное сложение по модулю 10" содержит все значения функции при переборе значений аргументов от 0 до 9 и относительно просто получается из таблицы десятичного полусумматора: 8765432109 7654321098 6543210987 5432109876 4321098765 3210987654 2109876543 1098765432 0987654321 9876543210 (пробелы отделяют по 10 знаков в номере функции).

Номер функции "единица переноса в следующий разряд при одноразрядном десятичном бинарном сложении" содержит все значения функции при переборе значений аргументов от 0 до 9 и тоже относительно просто получается из таблицы десятичного полусумматора: 1111111110 1111111100 1111111000 1111110000 1111100000 1111000000 1110000000 1100000000 1000000000 0000000000 (пробелы отделяют по 10 знаков в номере функции).

Так как в разряде переноса не бывает значения больше 1, то разряд переноса в одноразрядном десятичном полусумматоре является более простой десятичной функцией с унарным (одноразрядным) двоичным результатом (2 децита -> 1 бит).

Табличный одноразрядный десятичный полусумматор на Borland TurboBasic'е

'Half Adder Decimal Single-Digit
CLS
DATA 0,1,2,3,4,5,6,7,8,9
DATA 1,2,3,4,5,6,7,8,9,0
DATA 2,3,4,5,6,7,8,9,0,1
DATA 3,4,5,6,7,8,9,0,1,2
DATA 4,5,6,7,8,9,0,1,2,3
DATA 5,6,7,8,9,0,1,2,3,4
DATA 6,7,8,9,0,1,2,3,4,5
DATA 7,8,9,0,1,2,3,4,5,6
DATA 8,9,0,1,2,3,4,5,6,7
DATA 9,0,1,2,3,4,5,6,7,8

DATA 0,0,0,0,0,0,0,0,0,0
DATA 0,0,0,0,0,0,0,0,0,1
DATA 0,0,0,0,0,0,0,0,1,1
DATA 0,0,0,0,0,0,0,1,1,1
DATA 0,0,0,0,0,0,1,1,1,1
DATA 0,0,0,0,0,1,1,1,1,1
DATA 0,0,0,0,1,1,1,1,1,1
DATA 0,0,0,1,1,1,1,1,1,1
DATA 0,0,1,1,1,1,1,1,1,1
DATA 0,1,1,1,1,1,1,1,1,1

DEFINT I,J,F,A,B
FOR I=0 TO 9
  FOR J=0 TO 9
    READ F2DSM10[I,J]  'Function 2-argument Decimal Summ Mod 10 NonSymmetric
  NEXT J
NEXT I
FOR I=0 TO 9
  FOR J=0 TO 9
    READ F2DC10[I,J]   'Function 2-argument Decimal Carry Summ 10 NonSymmetric
  NEXT J
NEXT I

A=9
B=9
PRINT USING "#";A;
PRINT " + ";
PRINT USING "# = ";B;
PRINT USING "#";F2DC10[A,B];
PRINT USING "#";F2DSM10[A,B]
END

Врождённая способность

Исследования развития математических способностей, которые начались в 1980-х годах, рассматривали феномен привыкания: младенцы смотрят дольше на ситуации, которые являются для них неожиданными^[25]. В эксперименте Карен Винн^[англ.] 1992 года использовались куклы Микки Мауса, с которыми проводились различные манипуляции за ширмой. Этот эксперимент показал, что пятимесячные младенцы ожидают, что 1 + 1 — это 2, и удивляются тому, когда оказывается, что 1 + 1 — это 1 или 3. Позже этот результат был подтверждён в других лабораториях с использованием разных методов^[26]. В другом эксперименте в 1992 году с малышами постарше, в возрасте от 18 до 35 месяцев, использовалось развитие моторных функций детей, позволявшее им доставать шарики для пинг-понга из коробки; младшие ребята хорошо справлялись с небольшим числом шариков, более старшие научились считать сумму до 5^[27].

Даже некоторые животные проявляют способность складывать, в особенности приматы. Эксперимент 1995 года был аналогичен эксперименту Винн 1992 года, но вместо кукол использовались баклажаны. Выяснилось, что макаки-резусы и эдиповы тамарины показывают схожие человеческим младенцам способности. Более того, один шимпанзе, после того, как его научили различать и понимать смысл арабских цифр от 0 до 4, смог считать сумму двух чисел без какой-либо подготовки^[28]. Позже было выяснено, что азиатские слоны способны овладеть базовыми арифметическими операциями^[29].

Овладение сложением детьми

Как правило, сначала дети учатся подсчёту. Когда даётся задача, в которой требуется объединить два предмета и три предмета, маленькие дети обращаются к помощи конкретных предметов, например, счёт на пальцах или помощь рисунка. По мере приобретения опыта, они учат или открывают для себя стратегию «подсчёта»: когда требуется найти, сколько будет два плюс три, дети перечисляют два числа, идущие после числа три, проговаривая: «три, четыре, пять» (обычно загибая пальцы), и, в итоге, получая пять. Эта стратегия кажется почти универсальной; дети могут легко перенять её у сверстников или учителей^[30]. Многие дети сами доходят до этого. Накопив какой-то опыт, дети учатся складывать быстрее, используя коммутативность сложения, начиная перечислять числа от самого большого числа в сумме, как в описанном выше случае, начиная с трёх и перечисляя: «четыре, пять». В конце концов, дети начинают использовать какие-либо факты о сложении («примеры сложения наизусть^[англ.]»), получая их либо опытным путём, либо запоминая их. Когда одни факты осядут в памяти, дети начинают выводить неизвестные факты из известных. Например, ребёнок, складывающий шесть и семь, может знать, что 6 + 6 = 12, и что поэтому 6 + 7 на один больше, то есть 13^[31]. К такому способу вывода приходят довольно быстро и большинство учеников начальной школы полагаются на смесь всего того, что они запомнили и того, что они могут вывести, что в итоге позволяет им бегло складывать^[32].

В разных странах к изучению целых чисел и арифметики приступают в разных возрастах, в основном сложению учат в учреждениях дошкольного образования^[33]. При этом по всему миру к концу первого года начальной школы школьники обучаются сложению^[34].

Таблица сложения

Детям часто показывают таблицу сложения пар чисел от 1 до 10 для лучшего запоминания^{[обтекаемое выражение]}. Зная эту таблицу, можно выполнить любое сложение.

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18

таблица для сложения в десятичной системе счисления

Десятичная система

Для успешного сложения в десятичной системе нужно помнить или уметь быстро выводить 100 «фактов (примеров) сложения» для одноразрядных чисел. Кто-то может запомнить все эти факты, заучивая их, но стратегии изучения сложения путём использования шаблонов более информативны и для большинства людей более эффективны:^[35]

• Коммутативное свойство: использование шаблона ${\displaystyle a+b=b+a}$ снижает количество «фактов о сложении», которых нужно запомнить, со 100 до 55.
• На один или на два больше: прибавление 1 или 2 — это базовая задача, и решить её можно перечислением (подсчётом) или, в конце концов, полагаясь на интуицию^[35].
• Ноль: поскольку ноль является нейтральным элементом для операции сложения (аддитивной единицей), постольку прибавить ноль просто. Тем не менее, во время изучения арифметики некоторым ученикам сложение представляется как процесс, во время которого слагаемые всегда увеличиваются; акцент на словесной формулировке^[англ.] задачи может помочь понять «исключительность» нуля^[35].
• Удваивание: складывание числа с самим собой связано с задачей удвоенного (повторного) подсчёта и умножением. Факты об удваивании являются основой для многих связанных с ними фактов, и ученикам легко их относительно легко понять^[35].
• Почти-удваивание (Суммы, близкие к операции удваивания): сумма 6 + 7 = 13 может быть быстро выведена из факта об удваивании 6 + 6 = 12 и прибавления единицы, или из факта 7 + 7 = 14 и вычитания единицы^[35].
• Пять и десять: суммы вида 5 + x и 10 + x обычно запоминаются рано и могут быть использованы для выведения других фактов. Например, результат суммы 6 + 7 = 13 может быть выведен с использованием факта 5 + 7 = 12 добавлением к последнему единицы^[35].
• Получение десятки (достраивание до десяти): существует такая стратегия, в которой 10 используется в качестве промежуточного результата при наличии слагаемых 8 или 9; например, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14^[35].

По мере взросления ученики запоминают всё больше фактов, и учатся быстро выводить из них другие факты. Многие ученики не запоминают все факты, но могут быстро вывести требуемый^[32].

Перенос

В стандартном алгоритме сложения многоразрядных чисел^{[обтекаемое выражение]} цифры, из которых состоят записи складываемых чисел, располагаются одна под другой. Выполняют сложение цифр отдельно в каждом столбце, начиная с правого. Если сумма цифр в столбце превышает 10, лишняя цифра «переносится» в следующий столбец (левее). Например, в сумме 27 + 59

  ¹
  27
+ 59
————
  86

7 + 9 = 16 и цифра 1 переносится в следующий столбец. В альтернативном способе начинают сложение с наиболее значимой цифры слева; в этой стратегии перенос выполняется несколько грубее, но быстрее получается приблизительная сумма. Существует много других методов переноса.

Сложение десятичных дробей

Способ сложения десятичных дробей является простой модификацией сложения многоразрядных чисел, описанного выше^[36]. При сложении столбиком дроби располагают таким образом, чтобы запятые^[стиль] находились точно друг под другом. При необходимости можно добавлять нули справа и слева к более короткой дроби (см. замыкающий ноль^[англ.] и ведущие нули), чтобы сделать её равной по длине более длинной дроби. Итак, сложение производится таким же образом, как и в описанном выше способе сложения многоразрядных чисел, только запятая располагается в ответе точно там же, где она располагалась у слагаемых.

Например, сумму 45,1 + 4,34 можно вычислить следующим образом:

   4 5 , 1 0
+  0 4 , 3 4
————————————
   4 9 , 4 4

Экспоненциальная запись

В экспоненциальной записи числа записываются в виде ${\displaystyle a=\pm x\cdot P^{\pm n}}$, где ${\displaystyle x}$ — мантисса, ${\displaystyle P^{n}}$ — характеристика числа, ${\displaystyle P}$ — основание системы счисления. Для сложения двух чисел, которые записаны в экспоненциальной форме, требуется, чтобы у них были одинаковые характеристики: ${\displaystyle a\cdot P^{n}+b\cdot P^{n}=(a+b)\cdot P^{n},}$ согласно свойству дистрибутивности.

Например:

${\displaystyle 2.34\cdot 10^{-5}+5.67\cdot 10^{-6}=2.34\cdot 10^{-5}+0.567\cdot 10^{-5}=(2.34+0.567)\cdot 10^{-5}=2.907\cdot 10^{-5}}$

Особый случай — сложение чисел, различающихся на несколько порядков, с последовательным округлением. Если ${\displaystyle a\gg b}$, то и погрешности этих чисел будут несопоставимы (${\displaystyle \Delta a\gg \Delta b}$), и при выполнении сложения бо′льшая погрешность поглотит меньшую. Так может быть нарушено свойства ассоциативности.

Рассмотрим, например, выражение ${\displaystyle 5,6\cdot 10^{8}+7,2+(-5,6\cdot 10^{8})}$: если выполнить сначала ${\displaystyle 5,6\cdot 10^{8}+7,2}$, после округления результата получим ${\displaystyle \approx 5,6\cdot 10^{8}}$, складывая далее, имеем ${\displaystyle 5,6\cdot 10^{8}+(-5,6\cdot 10^{8})=0}$, а если выполнять сложение в ином порядке, то: ${\displaystyle 5,6\cdot 10^{8}+(-5,6\cdot 10^{8})+7,2=0+7,2=7,2}$. Таким образом, при неаккуратном округлении могут получиться различные значения одного и того же выражения.

Сложение в других системах счисления

Основная статья: Двоичная система счисления

Сложение для чисел с другими основаниями идентично сложению в десятичной системе

В качестве примера можно рассмотреть сложение в двоичной системе счисления^[37]. Сложение двух одноразрядных двоичных чисел с использованием переноса является довольно простым:

0 + 0 → 0

0 + 1 → 1

1 + 0 → 1

1 + 1 → 0, переносится 1 (так как 1 + 1 = 2 = 0 + (1 × 2¹))

Сумма двух знаков «1» равна знаку «0», а 1 должна быть добавлена в следующий столбец. Эта ситуация аналогична тому, что происходит в десятичной системе при суммировании определённых однозначных чисел; если результат равен или превышает значение основания системы счисления (10), цифры слева увеличиваются:

5 + 5 → 0, перенос 1 (так как 5 + 5 = 10 = 0 + (1 × 10¹))

7 + 9 → 6, перенос 1 (так как 7 + 9 = 16 = 6 + (1 × 10¹))

Эта операция известна как «перенос»^[38]. Когда результат сложения превосходит диапазон значений и разряда, нужно «перенести» избыток, делённый на основание системы (то есть на 10 в десятичной системе) влево, добавляя его к значению в следующем разряде. Это связано с тем, что значение в следующем разряде в ${\displaystyle N}$ раз больше (в ${\displaystyle N}$-ой системе счисления), чем значение в текущем разряде. Перенос в двоичной системе счисления работает также, как и в десятичной системе:

  1 1 1 1 1    (перенос)
    0 1 1 0 1
+   1 0 1 1 1
—————————————
  1 0 0 1 0 0 = 36

В этом примере складываются два числа: 01101₂ (13₁₀) и 10111₂ (23₁₀). В верхней строке указано наличие переноса. Начинаем складывать с правого столбца: 1 + 1 = 10₂. Здесь 1 переносится влево, а 0 записывается в нижней строке. Теперь складываются числа во втором столбце справа: 1 + 0 + 1 = 10₂; 1 переносится, а 0 записывается в нижней строке. Третий столбец: 1 + 1 + 1 = 11₂. В этом случае 1 переносится в нижней строке. В итоге получаем 100100₂ (или 36 в десятичной системе счисления).

Сложение в компьютерах

Сложение в аналоговых компьютерах

Электрическая схема сложения напряжений при помощи инвертирующего сумматора на операционном усилителе

Аналоговые компьютеры работают напрямую с физическими величинами, поэтому их механизм сложения зависит от вида слагаемых. Механический сумматор может представлять два слагаемых в виде позиций скользящих блоков, в этом случае их можно складывать при помощи усредняющего рычага. Если слагаемые представлены в виде углов поворота или угловых скоростей вращения двух валов, их можно сложить при помощи дифференциала.

Гидравлический сумматор может складывать давления в двух камерах, используя второй закон Ньютона, чтобы уравновесить силы на систему поршней.

Наиболее типичный случай применения аналогового компьютера — это сложение двух напряжений (относительно заземления); это можно приближённо выполнить при помощи пассивной резистивной схемы, а в точных аналоговых вычислений используется операционный усилитель^[39].

Цифровое сложение

Часть разностной машины Чарльза Бэббиджа включает механизмы сложения и переноса

Абак, также называемый счётной доской — это простейший вычислительный прибор, который использовался за много веков до распространения десятичной системы счисления и который всё ещё используется купцами, торговцами и клерками в Азии, Африке, и других континентах; предполагается, что абак изобретён не позднее 2700—2300 годов до н. э., тогда он начал использоваться шумерами^[40].

Блез Паскаль изобрёл механический калькулятор в 1642^[41][42]; это была первая операционная суммирующая машина. В этом калькуляторе механизм переноса работал используя действие тяжести. Это был единственный операционный калькулятор, созданный в 17 веке^[43] и самый первый цифровой компьютер. Недостаток машины Паскаля — механизм переноса, допускавший вращение цифровых колёс при сложении только в одну сторону. Для вычитания пользователь должен был использовать второй набор цифр на колёсах для представления результата и требовало такое же количество шагов, как и для сложения (методы дополнения^[англ.]).

Джованни Полени продолжил развитие калькулятора Паскаля, построив второй механический калькулятор в 1709 году. Циферблат этого калькулятора был из дерева, и однажды установленный он мог перемножать два числа между собой автоматически.

Операция сложения является основной в цифровых компьютерах. Скорость выполнения операции сложения и, в особенности, затраты времени на формирование межразрядного переноса, определяют, в частности, быстродействие компьютера.

Логическая схема одноразрядного двоичного сумматора складывающего три бита (разряды двоичного числа A, B и перенос от сложения битов предыдущего разряда C_in), выдаёт бит суммы по модулю 2 (S) и значение переноса (C_out) в следующий разряд

Сумматоры выполняющие целочисленное сложение в электронных цифровых вычислительных машинах, практически всегда использует бинарную арифметику. В простейшей структуре используется сумматор с последовательным переносом (выходной перенос предыдущего в цепочке сумматора является входным переносом для следующего сумматора), это позволяет выполнять сложение для многоразрядных чисел. Небольшое улучшение представлено в сумматоре с пропуском переноса^[англ.], который действует похожим с человеческой интуицией образом; например, он не выполняет все переносы в сумме 999 + 1, он обходит группу девяток и сразу выдаёт ответ^[44].

Практически сложение можно выполнять через сложение по модулю два и операцию «И» в сочетании с другими битовыми операциями, как показано ниже. Обе эти операции просто реализовать в цепях сумматоров, которые, в свою очередь, могут объединяться в более сложные логические операции.

В современных цифровых компьютерах сложение целых чисел, как и другие команды целочисленной арифметики, являются одними из самых быстрых операций, в то же время, они имеют существенное влияние на общую производительность компьютера, поскольку на целочисленные операции приходится существенная доля всех вычислений при выполнении любых программ. Целочисленное сложение используется, например, при вычислении адресов ячеек при доступе к памяти и при выборке команд во время определённого порядка их выполнения.

Для увеличения скорости работы современные компьютеры вычисляют значения в разрядах суммы параллельно; такие схемы называются «выборка переноса», предвидение переноса^[англ.] и псевдоперенос в сумматоре Линга^[англ.]. Обычно сложение на компьютере является гибридом последних трёх способов^[45][46].

В отличие от сложения человеком на бумаге, сложение на компьютере часто изменяет слагаемые в регистрах. На древнем абаке и доске для сложения при выполнении операции сложения оба слагаемых уничтожались, оставалась только их сумма. Влияние абака на математическое мышление было настолько велико, что в ранних латинских текстах часто утверждалось, что в процессе сложения «числа с числом» оба числа исчезают^[47]. В современных компьютерах обычно при выполнении инструкция ADD микропроцессор заменяет в регистре значение первого слагаемого полученной суммой, второе же слагаемое остаётся в регистре без изменений^[48].

В высокоуровневом языке программирования оценивание a + b не изменяет ни a, ни b; если ставится задача записать сумму в a, то это должно быть явно указано, например, выражение a = a + b. В некоторых языках программирования, таких как C или C++ эта запись упрощена до a += b.

Программа для иллюстрации логики суммирования двух битов и переноса

// Iterative Algorithm 
int add(int x, int y){
    int carry = 0;  
    while (y != 0){        
       carry = AND(x, y);   // Logical AND 
       x     = XOR(x, y);   // Logical XOR
       y     = carry << 1;  // left bitshift carry by one  
   } 
   return x;   
}
// Recursive Algorithm
int add(int x, int y){
   return x if (y == 0) else add(XOR(x, y) , AND(x, y) << 1); 
}

В случае если число разрядов результата сложения юольше разрядности регистров хранения, то происходит арифметическое переполнение, что приводит к неправильному результату или исключительной ситуации при выполнении программы. Непредвиденное арифметическое переполнение является довольно распространённой причиной программных ошибок. Такие ошибки переполнения может быть трудно обнаружить и диагностировать, потому что они могут проявляться только при некоторых наборах входных данных, которые не были использованы в тестах^[49].

Сложение вещественных чисел на современных компьютерах, как и все вычисления с плавающей точкой, выполняются аппаратно специальным устройством, называемом математическим сопроцессором (название условное, так как в современных компьютерах физически он встроен в центральный процессор). При выполнении операции сложения с плавающей точкой также возможно переполнение, однако оно всегда вызывает обработку исключений, и обнаруживается.

Ещё одной важной особенностью компьютерных вычислений с плавающей точкой является ограниченная точность представления вещественного числа, в связи с чем вычисления с плавающей точкой на компьютере выполняются, вообще говоря, приближённо, а к результатам вычислений (в том числе, промежуточным) применяется операция округления. Округление, как правило, применяется даже к тем числам, которые в десятичной системе счисления представлены конечной дробью, то есть точно (поскольку в наиболее распространённых компьютерах применяется двоичная система счисления). Поэтому при суммировании на компьютере чисел с плавающей точкой сумма может зависеть от очерёдности суммирования слагаемых — иногда существенно, если порядки слагаемых многократгно отличаются. Поэтому в программах, где суммируется много переменных, применяют специальные меры для снижение погрешности. Одним из наиболее эффективных методов снижения погрешности суммирования является алгоритм Кэхэна.

Сложение чисел

Для представления основных свойств сложения сначала нужно определиться с контекстом. Изначально сложение определено для натуральных чисел. Сложение определяется для всё больших и больших множеств, включая натуральные числа: целые числа, рациональные числа и вещественные числа^[50]. (В математическом образовании^[51] сложение положительных дробей проходят до сложения отрицательных чисел^[52].)

Натуральные числа

Воспользуемся определением натуральных чисел ${\displaystyle \mathbb {N} }$ как классов эквивалентности конечных множеств. Обозначим классы эквивалентности конечных множеств ${\displaystyle C,A,B}$ порождённых биекциями, с помощью скобок: ${\displaystyle [C],[A],[B]}$. Тогда арифметическая операция «сложение» определяется следующим образом:

${\displaystyle [C]=[A]+[B]=[A\sqcup B];}$

где ${\displaystyle A\sqcup B}$ — дизъюнктное объединение множеств. Данная операция на классах введена корректно, то есть не зависит от выбора элементов классов, и совпадает с индуктивным определением.

Взаимно однозначное отображение конечного множества ${\displaystyle A}$ на отрезок ${\displaystyle N_{a}}$ можно понимать как нумерацию элементов множества ${\displaystyle A:\quad A\sim N_{a}}$ . Этот процесс нумерации называют «счётом»^{[53][уточнить ссылку 1286 дней]}. Таким образом, «счёт» - это установление взаимно-однозначного соответствия между элементами множества и отрезком натурального ряда чисел^[54].

Для сложения натуральных чисел в позиционной системе обозначения чисел применяется поразрядный алгоритм сложения. Если даны два натуральных числа ${\displaystyle a}$ и ${\displaystyle b}$ такие, что:

${\displaystyle a=a_{n-1}a_{n-2}\dots a_{0},\quad b=b_{n-1}b_{n-2}\dots b_{0},\quad \forall a_{k},b_{k}\in \{P\}\quad \forall a_{n-1},b_{n-1}\neq 0\quad \exists 0\in \mathbb {N}$ ;}

где: ${\displaystyle a_{0\dots n-1}=a_{k}P^{k},\quad b_{0\dots n-1}=b_{k}P^{k}}$;

${\displaystyle n}$ - количество цифр в числе ${\displaystyle n\in \{1,2,\dots ,n\}}$;

${\displaystyle k}$ - порядковый номером разряда (позиции), ${\displaystyle k\in \{0,1,\dots ,n-1\}}$;

${\displaystyle P}$ - основание системы счисления;

${\displaystyle \{P\}}$ множество числовых знаков (цифр), конкретной системы счисления:

${\displaystyle \{P_{2}\}=\{0,1\}}$,

${\displaystyle \{P_{10}\}=\{0,1,2,3,4,5,6,7,8,9\}}$,

${\displaystyle \{P_{16}\}=\{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F\}}$;

тогда:

${\displaystyle c=a+b;\quad c_{n-1}c_{n-2}\dots c_{0}=a_{n-1}a_{n-2}\dots a_{0}+b_{n-1}b_{n-2}\dots b_{0};}$

складывая поразрядно, получаем:

• ${\displaystyle c_{0}={\begin{cases}a_{0}+b_{0},\quad c_{1}=0&{\text{if }}a_{0}+b_{0}\leqslant P-1{\text{ }}\\a_{0}+b_{0}-P,\quad c_{1}=1&{\text{if }}a_{0}+b_{0}>P-1{\text{ }}\end{cases}}}$
• ${\displaystyle c_{1}={\begin{cases}a_{1}+b_{1}+c_{1},\quad c_{2}=0&{\text{if }}a_{1}+b_{1}+c_{1}\leqslant P-1{\text{ }}\\a_{1}+b_{1}+c_{1}-P,\quad c_{2}=1&{\text{if }}a_{1}+b_{1}+c_{1}>P-1{\text{ }}\end{cases}}}$
• ${\displaystyle ...\quad \quad ...\quad \quad ...}$
• ${\displaystyle c_{n-1}={\begin{cases}a_{n-1}+b_{n-1}+c_{n-1},\quad c_{n}=0&{\text{if }}a_{n-1}+b_{n-1}+c_{n-1}\leqslant P-1{\text{ }}\\a_{n-1}+b_{n-1}+c_{n-1}-P,\quad c_{n}=1&{\text{if }}a_{n-1}+b_{n-1}+c_{n-1}>P-1{\text{ }}\end{cases}}}$

Таким образом, операция сложения сводится к процедуре последовательного простого сложения одноразрядных чисел ${\displaystyle a_{k}+b_{k}}$, с формированием единицы переноса при необходимости, которое производится либо табличным методом, либо инкрементированием (счётом).

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами^[55]. При этом нужно пользоваться таблицей сложения, соответствующей данному основанию ${\displaystyle P}$ системы счисления.

Пример сложения натуральных чисел в двоичной, десятичной и шестнадцатеричной системах счисления, для удобства числа записываются друг под другом соответственно разрядам, единица переноса пишется сверху, недостающие разряды дополняются нулями:

${\displaystyle {\begin{array}{ccccccccc}&_{1}&_{1}&_{1}\\&0&1&0&1&1&0\\+&1&1&1&1&0&1\\\hline 1&0&1&0&0&1&1\end{array}};\quad \quad {\begin{array}{ccccccc}&_{1}&_{1}&_{1}\\&3&4&5&6&7\\+&8&7&5&4&1\\\hline 1&2&2&1&0&8\end{array}};\quad \quad {\begin{array}{ccccccc}&_{1}&&_{1}&_{1}&_{1}\\&C&5&6&D&E&4\\+&0&F&2&A&1&F\\\hline &D&4&9&8&0&3\end{array}}.}$

Другое известное определение рекурсивно:

• Пусть n⁺ — следующее^[англ.] за n натуральное число, например 0⁺=1, 1⁺=2. Пусть a + 0 = a. Тогда общая сумма определяется рекурсивно: a + (b⁺) = (a + b)⁺. Отсюда 1 + 1 = 1 + 0⁺ = (1 + 0)⁺ = 1⁺ = 2^[56].

В литературе существуют различные варианты этого определения. В рекурсионной теореме^{[неизвестный термин]} на частично упорядоченном множестве N² используется в точности определение, данное выше^[57]. С другой стороны, в некоторых источниках предпочитают использовать ограниченную Рекурсионную теорему, которая применяется только к множеству натуральных чисел. Одни предлагают временно «зафиксировать» a, применяя рекурсию на b, чтобы определить функцию "a + ", и вставлять эти унарные операции для всех a, чтобы сформировать полную бинарную операцию^[58].

Это рекурсивное определение сложения было дано Дедекиндом ещё в 1854 году, и он расширил его в последующие десятилетия^[59]. С помощью математической индукции Дедекинд доказал свойства ассоциативности и коммутативности.

Целые числа

Иллюстрация правил сложения положительных и отрицательных чисел.

Сложить (−2) и 1, используя только положительные числа: (2 − 4) + (3 − 2) = 5 − 6.

Множество целых чисел — расширение множества натуральных чисел ${\displaystyle \mathbb {N} }$, получаемое добавлением отрицательных чисел ^[60] вида ${\displaystyle -n}$. Множество целых чисел обозначается ${\displaystyle \mathbb {Z} .}$ Арифметические операции над целыми числами определяются как непрерывное продолжение соответствующих операций над натуральными числами. Отличие от натуральных чисел состоит в том, что отрицательные числа на числовой прямой направлены в противоположную сторону, это несколько меняет процедуру сложения. Необходимо учитывать взаимное направление чисел, здесь возможны несколько случаев:

Положительное и отрицательное числа на числовой прямой.

• Если оба слагаемых положительные, тогда: ${\displaystyle c=a+b;}$
• Если одно из слагаемых отрицательно, тогда нужно от слагаемого с большим значением модуля вычесть слагаемое с меньшим значением модуля, после чего перед полученным числом поставить знак того слагаемого, модуль которого больше: ${\displaystyle c=-a+b=b+(-a)=b-a;}$
• Если оба слагаемых отрицательны, тогда: ${\displaystyle c=(-a)+(-b)=-(|a|+|b|)}$ ^[61].

Другое построение множества целых чисел основано на группах Гротендика. Главная идея заключается в том, что каждое целое число может быть представлено (не одним способом) как разность двух натуральных чисел, поэтому мы можем определить целое число, как разность двух натуральных чисел. Тогда сложение определяется следующим образом:

• Пусть имеются два целых числа a − b и c − d, где a, b, c и d — натуральные числа, тогда (a − b) + (c − d) = (a + c) − (b + d)^[62].

Рациональные числа

Множество рациональных чисел обозначается ${\displaystyle \mathbb {Q} }$ (от англ. quotient «частное») и может быть записано в таком виде: ${\displaystyle \mathbb {Q} =\left\{{\frac {m}{n}}\mid m\in \mathbb {Z} ,n\in \mathbb {N} \right\}.}$

Для сложения рациональных чисел в виде обыкновенных (или простых) дробей вида: ${\displaystyle \pm {\frac {m}{n}}}$, их следует преобразовать (привести) к общему (одинаковому) знаменателю. Например, взять произведение знаменателей, числители при этом умножаются на соответствующие знаменатели. Затем сложить полученные числители, а произведение знаменателей станет общим.

Если даны два рациональных числа ${\displaystyle a}$ и ${\displaystyle b}$ такие, что: ${\displaystyle a={\frac {m_{a}}{n_{a}}},b={\frac {m_{b}}{n_{b}}}\quad \forall m_{a},n_{a},m_{b},n_{b}\in \mathbb {N} \quad \forall {n_{a}},{n_{b}}\neq 0}$ (дроби несократимые), тогда:

${\displaystyle c=a+b={\frac {m_{a}}{n_{a}}}+{\frac {m_{b}}{n_{b}}}={\frac {m_{a}\cdot n_{b}}{n_{a}\cdot n_{b}}}+{\frac {n_{a}\cdot m_{b}}{n_{a}\cdot n_{b}}}={\frac {m_{a}\cdot n_{b}+m_{b}\cdot n_{a}}{n_{a}\cdot n_{b}}}.}$ ^[63]

Либо можно найти наименьшее общее кратное (НОК) знаменателей. Порядок действий:

• Находим наименьшее общее кратное знаменателей: ${\displaystyle M=[n_{a},n_{b}]}$.
• Умножаем числитель и знаменатель первой дроби на ${\displaystyle {\frac {M}{n_{a}}}}$.
• Умножаем числитель и знаменатель второй дроби на ${\displaystyle {\frac {M}{n_{b}}}}$.

После этого знаменатели обеих дробей совпадают (равны ${\displaystyle M}$). В ряде простых случаев это упрощает вычисления, но в случае больших чисел расчёты значительно усложняются. Можно взять в качестве ${\displaystyle M}$ любое другое общее кратное.

Пример сложения:

${\displaystyle {\frac {2}{3}}+{\frac {1}{5}}={\frac {2\cdot 5}{3\cdot 5}}+{\frac {3\cdot 1}{3\cdot 5}}={\frac {2\cdot 5+3\cdot 1}{3\cdot 5}}={\frac {10+3}{15}}={\frac {13}{15}}.}$

Если знаменатели обеих дробей совпадают, то:

${\displaystyle {\frac {1}{4}}+{\frac {2}{4}}={\frac {1+2}{4}}={\frac {3}{4}}.}$

Если знаменатели кратны какому-либо числу, то преобразуем только одну дробь:

${\displaystyle {\frac {3}{8}}+{\frac {1}{4}}={\frac {3}{8}}+{\frac {1\cdot 2}{4\cdot 2}}={\frac {3+1\cdot 2}{8}}={\frac {5}{8}}.}$

Арифметическая операция «сложение» над рациональными числами относится к замкнутым операциям. Коммутативность и ассоциативность сложения рациональных чисел — следствие законов целочисленной арифметики^[64]. Более строгое и общее определение см. в статье поле дробей.

Аналогичным образом складываются физические величины: их выражают через общие единицы измерения^[65]. Например, чтобы сложить 50 миллилитров и 1,5 литра, необходимо перевести миллилитры в литры и привести дроби к общему знаменателю: ${\displaystyle {\frac {50}{1000}}+{\frac {1500}{1000}}={\frac {1550}{1000}}=1{,}55}$ литра.

Вещественные числа

Арифметические операции над вещественными числами, представимыми в виде бесконечных десятичных дробей, определяются как непрерывное продолжение^[66] соответствующих операций над рациональными числами.

Если даны два вещественных числа, представимые бесконечными десятичными дробями:

${\displaystyle \alpha =\pm a_{0},a_{1}a_{2}\ldots a_{n}\ldots =\{a_{n}\}}$, ${\displaystyle \beta =\pm b_{0},b_{1}b_{2}\ldots b_{n}\ldots =\{b_{n}\}}$

определённые соответственно фундаментальными последовательностями рациональных чисел (удовлетворяющие условию Коши), обозначенные как: ${\displaystyle \alpha =[a_{n}]}$ и ${\displaystyle \beta =[b_{n}]}$, то их суммой называют число ${\displaystyle \gamma =[c_{n}]}$, определённое суммой последовательностей ${\displaystyle \{a_{n}\}}$ и ${\displaystyle \{b_{n}\}}$:

${\displaystyle \gamma =\alpha +\beta {\overset {\text{def}}{=}}[a_{n}]+[b_{n}]=[a_{n}+b_{n}]}$;

вещественное число ${\displaystyle \gamma =\alpha +\beta }$, удовлетворяет следующему условию:

${\displaystyle \forall a',a'',b',b''\in \mathbb {Q}$ ;(a'\leqslant \alpha \leqslant a'')\land (b'\leqslant \beta \leqslant b'')\Rightarrow (a'+b'\leqslant \alpha +\beta \leqslant a''+b'')\Rightarrow (a'+b'\leqslant \gamma \leqslant a''+b'')} .

Таким образом, сумма двух вещественных чисел ${\displaystyle \alpha }$ и ${\displaystyle \beta }$ — такое вещественное число ${\displaystyle \gamma }$, которое содержится между всеми суммами вида ${\displaystyle a'+b'}$ с одной стороны и всеми суммами вида ${\displaystyle a''+b''}$ с другой стороны^[67].

На практике для того, чтобы сложить два числа ${\displaystyle \alpha }$ и ${\displaystyle \beta }$, необходимо заменить их с требуемой точностью приближёнными рациональными числами ${\displaystyle a}$ и ${\displaystyle b}$. За приближённое значение суммы чисел ${\displaystyle \alpha +\beta }$ берут сумму указанных рациональных чисел ${\displaystyle a+b}$. При этом не важно, с какой стороны (по недостатку или по избытку) взятые рациональные числа приближают ${\displaystyle \alpha }$ и ${\displaystyle \beta }$. Сложение производится по алгоритму поразрядного сложения.

При сложении приближённых чисел их абсолютные погрешности складываются ${\displaystyle \Delta (a+b)=\Delta a+\Delta b}$, абсолютная погрешность числа принимается равной половине последнего знака этого числа. Относительная погрешность суммы заключена между наибольшим и наименьшим значениями относительных погрешностей слагаемых; на практике принимается наибольшее значение ${\displaystyle \delta (a+b)=max(\delta a,\delta b)}$. Полученный результат округляют до первой верной значащей цифры, значащая цифра приближённого числа верна, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.

Пример сложения ${\displaystyle \gamma =\pi +e}$, с точностью до 3-го знака после запятой:

• Округляем данные числа до 4-го знака после запятой (для повышения точности вычислений);
• Получаем: ${\displaystyle \pi \approx 3.1416,\quad e\approx 2.7183}$ ;
• Поразрядно складываем: ${\displaystyle \gamma =\pi +e\approx 3.1416+2.7183\approx 5.8599}$ ;
• Округляем до 3-го знака после запятой: ${\displaystyle \gamma \approx 5.860}$ .

График

На множестве вещественных чисел график функции сложения имеет вид плоскости, проходящей через начало координат и наклонённой к осям на 45° угловых градусов. Так как ${\displaystyle \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} }$, то и для этих множеств значения функции сложения будет принадлежать этой плоскости^[68].

График функции f(c)=a+b

Комплексные числа

Сложение двух комплексных чисел может быть представлено геометрически через построение параллелограмма.

Комплексные числа складываются друг с другом путём сложения действительных и мнимых частей^[69]. Это значит, что:

${\displaystyle c+fi=(a+di)+(b+ei)=(a+b)+(d+e)i.\ }$

Где: ${\displaystyle c,a,b,d,e,f\in \mathbb {R} }$, ${\displaystyle i}$ — мнимая единица .Используя представление комплексных чисел как точек на комплексной плоскости, можно дать сложению комплексных чисел следующую геометрическую интерпретацию: суммой комплексных чисел ${\displaystyle a+di}$ и ${\displaystyle b+ei}$, представленных точками на комплексной плоскости, является точка C, полученная путём построения параллелограмма, три вершины которого находятся в точках O, A и B. Или, можно сказать, что C — это такая точка, что треугольники OAB и CBA конгруэнтны.

Аналогично для гиперкомплексных чисел (комплексных чисел n-ой размерности): ${\displaystyle A=a_{1}1+a_{2}i_{2}+\dots +a_{n}i_{n},~~~B=b_{1}1+b_{2}i_{2}+\dots +b_{n}i_{n};}$ ${\displaystyle C=A+B=(a_{1}1+a_{2}i_{2}+\dots +a_{n}i_{n})+(b_{1}1+b_{2}i_{2}+\dots +b_{n}i_{n})=}$ ${\displaystyle =(a_{1}+b_{1})1+(a_{2}+b_{2})i_{2}+\dots +(a_{n}+b_{n})i_{n}=c_{1}1+c_{2}i_{2}+\dots +c_{n}i_{n}.}$ ^[70]

Сложение произвольных чисел

При сложении чисел, принадлежащих разным множествам, необходимо (если возможно) представить множество с меньшей мощностью как подмножество множества с большей мощностью, либо найти «наименьшее общее множество». Например, если нужно сложить натуральное число ${\displaystyle 3}$ с рациональным ${\displaystyle 4,56}$, то, воспользовавшись тем, что натуральные числа — подмножество рациональных, представляем число ${\displaystyle 3}$ как рациональное ${\displaystyle 3,00}$ и складываем два рациональных числа ${\displaystyle 3,00+4,56=7,56}$. Аналогично, пользуясь тем, что: ${\displaystyle \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} \subset \mathbb {H} }$, можно складывать числа из различных множеств между собой. Возвращаясь к примеру с яблоками, воспользуемся тем, что множество яблок и множество груш — подмножества множества фруктов: ${\displaystyle \{{\mbox{apple}}\}\subset \{{\text{apples}}\}\subset \{{\text{fruit}}\}~~~{\text{end}}~~~\{{\text{pear}}\}\subset \{{\text{pears}}\}\subset \{{\text{fruit}}\}}$, и таким образом можно сложить 3 яблока и 2 груши, представив их как подмножества множества фруктов: ${\displaystyle 3}$ фрукта_яблока ${\displaystyle +2}$ фрукта_груши ${\displaystyle =5}$ фруктов.

Обобщения

Существует много бинарных операций, которые можно рассматривать как обобщения операции сложения действительных чисел. Такие обобщённые операции являются основным предметом изучения общей алгебры, также они встречаются в теории множеств и теории категорий.

Сложение в абстрактной алгебре

Сложение векторов

Векторное пространство — это алгебраическая структура, в которой любые два вектора можно складывать и любой вектор можно умножать на число. Простой пример векторного пространства — множество всех упорядоченных пар действительных чисел; упорядоченная пара ${\displaystyle (a,b)}$ — это вектор с началом в точке ${\displaystyle (0,0)}$ евклидовой плоскости и концом в точке ${\displaystyle (a,b)}$ (и все сонаправленные ему). Сумма двух векторов получается путём сложения их соответствующих координат: ${\displaystyle (a,b)+(c,d)=(a+c,b+d)}$. Эта операция сложения — центральная в классической механике, в которой векторы рассматриваются как аналоги сил.

Сложение матриц

Основная статья: Сложение матриц

Сложение матриц определяется для двух матриц одинакового размера. Сумма двух матриц A и B размера m × n (произносится «m на n»), записывается как A + B и представляет собой матрицу размера m × n, полученную путём сложения соответствующих элементов^[71][72]:

${\displaystyle {\begin{aligned}\mathbf {A} +\mathbf {B} &={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{bmatrix}}+{\begin{bmatrix}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\\\end{bmatrix}}\\&={\begin{bmatrix}a_{11}+b_{11}&a_{12}+b_{12}&\cdots &a_{1n}+b_{1n}\\a_{21}+b_{21}&a_{22}+b_{22}&\cdots &a_{2n}+b_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots &a_{mn}+b_{mn}\\\end{bmatrix}}\\\end{aligned}}}$

Например:

${\displaystyle {\begin{bmatrix}1&3\\1&0\\1&2\end{bmatrix}}+{\begin{bmatrix}0&0\\7&5\\2&1\end{bmatrix}}={\begin{bmatrix}1+0&3+0\\1+7&0+5\\1+2&2+1\end{bmatrix}}={\begin{bmatrix}1&3\\8&5\\3&3\end{bmatrix}}}$

Арифметика остатков

Основная статья: Сравнение по модулю

Множество остатков от деления на 12 состоит из двенадцати элементов; это множество наследует операцию сложения целых чисел. Множество остатков по модулю 2 имеет только два элемента; наследуемая им операция сложения известна в логике высказываний как операция «исключающее или». В геометрии сумма двух угловых мер часто определяется как сумма вещественных чисел по модулю 2π. Такое определение соответствует операции сложения на окружности, которая, в свою очередь, обобщается до операции сложения на многомерном торе.

Общее сложение

В общей теории абстрактной алгебры операцией «сложения» может называться любая ассоциативная и коммутативная операция. Основные алгебраические системы с такими операциями сложения включают коммутативные моноиды и абелевы группы.

Сложение в теории множеств и теории категорий

Обобщением сложения натуральных чисел является сложение порядковых чисел и кардинальных чисел в теории множеств. Эти операции представляют собой два разных обобщения сложения натуральных чисел на трансфинитный случай. В отличие от большинства типов операции сложения, сложение порядковых чисел не коммутативно. Сложение кардинальных чисел, тем не менее, является коммутативной операцией, тесно связанной с операцией дизъюнктного объединения.

В теории категорий дизъюнктное объединение рассматривается как частный случай операции копроизведения, и общие копроизведения, возможно, являются самыми абстрактными из всех обобщений операции сложения. Некоторые копроизведения, такие как прямая сумма и клиновая сумма^[англ.], названы так, чтобы указывать на их связь с операцией сложения.

Операции, связанные со сложением

Сложение, так же, как и вычитание, умножение и деление, считается одной из основных операций и используется в элементарной арифметике.

Арифметика

Вычитание можно рассматривать как частный случай операции сложения, а именно — как прибавление противоположного числа. Вычитание само по себе является своего рода обратной операцией к сложению, то есть прибавление x и вычитание x являются взаимно обратными функциями.

На множестве чисел, на котором определена операция сложения, не всегда можно определить операцию вычитания; простым примером является множество натуральных чисел. С другой стороны, операция вычитания однозначно определяет операцию сложения и аддитивную единицу; по этой причине аддитивную группу можно определять как множество, замкнутое относительно операции вычитания^[73].

Умножение можно понимать как повторённое несколько раз сложение^[англ.]. Если терм x входит в сумму n раз, то эта сумма равна произведению n и x. Если n не является натуральным числом, произведение всё ещё может иметь смысл; например, умножение на -1 даёт противоположное число.

Круговая логарифмическая линейка

Сложение и умножение действительных или комплексных чисел можно взаимно заменять при помощи экспоненциальной функции:

e^{a + b} = e^a e^b[74].

Это тождество позволяет умножать, используя таблицы^[англ.] логарифмов и сложение вручную; оно также позволяет умножать с использованием логарифмической линейки. Эта формула является также хорошим приближением первого порядка в широком контексте групп Ли, где она связывает умножение бесконечно малых элементов группы Ли со сложением векторов в соответствующей алгебре Ли^[75].

У умножения есть даже больше обобщений, чем у сложения^[76]. Вообще говоря, операции умножения всегда дистрибутивны относительно сложения. Это требование закреплено в определении кольца. В некоторых случаях, таких как целые числа, дистрибутивности умножения относительно сложения и наличия мультипликативной единицы достаточно, чтобы однозначно определить операцию умножения. Свойство дистрибутивности также характеризует сложение; раскрывая скобки в произведении (1 + 1)(a + b) двумя способами, приходим к выводу, что сложение должно быть коммутативным. По этой причине сложение в кольце всегда коммутативно^[77].

Деление — это арифметическая операция, отдалённо связанная со сложением. Поскольку a/b = a(b⁻¹), деление является дистрибутивным справа относительно сложения: (a + b) / c = a / c + b / c^[78]. Тем не менее, деление не является дистрибутивным слева относительно сложения; 1/ (2 + 2) не равняется 1/2 + 1/2.

Упорядочивание

График в логарифмическом масштабе по обеим осям^[англ.] функций x + 1 и max (x, 1) для x от 0.001 до 1000^[79]

Операция нахождения максимума «max (a, b)» — это бинарная операция, похожая на сложение. На самом деле, если два неотрицательных числа a и b имеют различные порядки, то их сумма примерно равна их максимуму. Это приближение является чрезвычайно полезным в приложениях математики, например, при усечении ряда Тейлора. Тем не менее, эта операция приводит к постоянным трудностям в численном анализе, так как операция взятия максимума не является обратимой. Если b намного больше, чем a, то обычное вычисление (a + b) − b может привести к накоплению неприемлемой ошибки округления^[англ.], возможно получение нулевого результата. См. также потеря значимости^[англ.].

Это приближение становится точным при переходе к бесконечному пределу^{[уточнить]}; если какое-либо из чисел a и b является кардинальным числом, то их кардинальная сумма в точности равна большему из двух^[80]. Соответственно, операция вычитания не определена для множеств бесконечной мощности^[81].

Нахождение максимума является коммутативной и ассоциативной операцией, как и сложение. Более того, поскольку сложение сохраняет упорядочение действительных чисел, сложение дистрибутивно по отношению к функции нахождения максимума таким же образом, как и умножение по отношению к сложению:

a + max (b, c) = max (a + b, a + c).

По этим причинам в тропической геометрии умножение заменяется на сложение, а сложение — на нахождение максимума. В этом контексте сложение называют «тропическим умножением», нахождение максимума — «тропическим сложением», а тропическую «аддитивную единицу» — отрицательной бесконечностью^[82]. Некоторые авторы предпочитают заменять сложение минимизацией; в этом случае аддитивной единицей является положительная бесконечность^[83].

Объединяя эти наблюдения вместе, тропическое сложение приблизительно соответствует обычному сложению при помощи логарифма:

log (a + b) ≈ max (log a, log b),

что становится более точным при возрастании основания логарифма^[84]. Приближение может стать точным, если выделить константу h, названную по аналогии с постоянной Планка в квантовой механике^[85], и взять "классический предел"^[англ.], при котором h стремится к нулю:

${\displaystyle \max(a,b)=\lim _{h\to 0}h\log(e^{a/h}+e^{b/h}).}$

В этом смысле операция нахождения максимума является деквантизацией сложения^[86].

Другие способы сложения

Инкрементирование, или применение функции следования — это прибавление 1 к числу.

Суммирование — это сложение сколь угодно большого количества чисел, обычно больше, чем двух. Частными случаями этого понятия являются суммирование одного числа (результат такого суммирования равен самому числу), а также пустая сумма^[англ.], равная нулю^[87]. Бесконечное суммирование — нетривиальная процедура, известная как нахождение суммы ряда^[88].

Суммирование единичной функции по конечному множеству даёт тот же результат, что и подсчёт числа элементов этого множества.

Интегрирование — это своего рода «суммирование» по континууму или, более точно и общо, по гладкому многообразию. Интегрирование по множеству нулевой размерности сводится к суммированию.

Линейные комбинации совмещают умножение и суммирование; это суммы, в которых каждый член имеет множитель, обычно действительное или комплексное число. Линейные комбинации особенно полезны в тех ситуациях, когда обычное сложение нарушило бы некоторое правило нормализации, как, например, при смешивании стратегий в теории игр или суперпозиции состояний в квантовой механике.

Свёртка используется для сложения двух независимых случайных величин, заданных функциями распределения. В стандартном определении свёртки используются интегрирование, вычитание и умножение. В целом, свёртку уместно рассматривать как «сложение на области определения», а векторное сложение — как «сложение на области значений».

См. также

• Соглашение Эйнштейна
• Сумма
• Алгоритм Кэхэна
• Вычитание
• Умножение
• Деление

Примечания

1. Эндертон, 1977, p. 138: «…выберите два набора K и L с мощностью K = 2 и мощностью L = 3. Наборы из пальцев удобны; в учебниках предпочитают использовать наборы из яблок.».
2. Рудницкая, 2004, с. 110.
3. Иванова О. А. Сложение, 1984.
4. Порядок выполнения операций, 2012.
5. Сложение, 1988.
6. Сложение, 1976.
7. Системы счисления, 2006, с. 3.
8. Девайн и соавторы, 1991, с. 263.
9. Мазур, 2014, с. 161.
10. Словарь русского языка, 1999, с. 130.
11. Каджори, 1928.
12. Оксфордский словарь английского языка, 2005.
13. Виро, 2012, с. 5.
14. Килпатрик, 2001: «Например, дюймы могут быть разделены на части, которые трудно отличить от целых дюймов, за исключением того, что они получаются более короткими; но деление на части будет болезненно для кошек, и это действие серьёзно изменит их природу.».
15. Мосли, 2001, с. 8.
16. Ли Я., 2013, с. 204.
17. Так эти свойства называются в учебниках для младших классов
18. Каплан, 1999, pp. 69—71.
19. Свойства сложения, 2016, Свойства сложения, умножения, вычитания и деления целых чисел, Сумма с противоположным числом, с. 1.
20. Зельвенский, [б. г.], с. 18.
21. Чёрный я́щик — термин, используемый для обозначения системы, внутреннее устройство и механизм работы которой очень сложны, неизвестны или неважны в рамках данной задачи. «Метод чёрного ящика» — метод исследования таких систем, когда вместо свойств и взаимосвязей составных частей системы, изучается реакция системы, как целого, на изменяющиеся условия.
22. Эшби, 1959, Введение в кибернетику, с. 127-169.
23. Зубарева, 2013, с. 195.
24. Алгоритм сложения, с. 1.
25. Винн, 1998, с. 5.
26. Винн, 1998, с. 15.
27. Винн, 1998, с. 17.
28. Винн, 1998, с. 19.
29. У слонов достаточно ума, чтобы рисовать фигуры, 2008.
30. Смит Ф., 2002, с. 130.
31. Карпентер и др., 2014.
32. Генри Валери Д., 2008, pp. 153—183.
33. Изучение математики в начальной школе в целых числах, 2014, pp. 1—8.
34. Последовательность обучения, 2002, pp. 1—18.
35. Фоснот и Долк, 2001, с. 99.
36. Вингард-Нельсон Р., 2014, с. 21.
37. Дейл, 2008, с. 155.
38. Ботман, 1837, с. 31.
39. Трайт и Рождерс, 1960, pp. 41—49.
40. Джорджс, 2001, с. 11.
41. Маргун, 1994, с. 48.
42. Танон, 1963, с. 62.
43. См. конкурирующие конструкции в статье о суммирующей машине Паскаля
44. Флинн и Оверман, 2001, pp. 2—8.
45. Флинн и Оверман, 2001, pp. 1—9.
46. Санг-Су Йо, 2010, с. 194.
47. Карпински, 1925, pp. 102—103.
48. Хоровец и Хилл, 2009, с. 679.
49. Блотч, 2006, с. 1.
50. Эндертон, 1977, pp. 4—5.
51. Последовательность обучения, 2002, с. 4.
52. Baez, 2000, с. 37: «Очевидно, что представить половину яблока легче, чем отрицательное яблоко!».
53. нумерация, Теоретические основы введения целых неотрицательных чисел, с. 7.
54. Истомина, 2009, с. 71.
55. Системы счисления, 2006, с. 3.
56. Эндертон, 1977, с. 79.
57. Бергман, 2015, p. 100: «См. в книге Бергмана версию, применимую к любому частично упорядоченному множеству с нисходящей цепочкой состояний^[англ.].».
58. Эндертон, 1977, p. 79: «Но нам нужна одна бинарная операция +, а не все эти маленькие одноместные функции.».
59. Ферриус, 2013, с. 223.
60. Выгодский, 2003.
61. Барсуков, 1966, с. 25.
62. Эндертон, 1977, с. 92.
63. Гусев, 1988, с. 20.
64. Эндертон, 1977, с. 104.
65. Фиерро, 2012, с. 87.
66. Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида ${\displaystyle \{x:\alpha <x<\beta \}}$
67. Ильин, 1985, с. 46.
68. График выполнен программой «3D Grapher Версия 1.2», www.romanlab.com. Входные аргументы: x=a, y=b, z=a+b
69. Конвей, 1986, с. 107.
70. Александров, 1956, с. 304.
71. Липсхатз, 2001, с. 201.
72. Рили, 2006, с. 253.
73. Даммит и Фут, 1999, с. 48.
74. Рудин, 1976, с. 178.
75. Ли Ж., 2013, с. 526.
76. Линдерхолм, 1972, p. 49.
77. Даммит и Фут, 1999, с. 224: «Чтобы это выполнялось, необходимо, чтобы сложение было групповой операцией и существовал нейтральный элемент относительно умножения.».
78. Лодей, 2002, p. 15: «Пример дистрибутивности слева и справа см. в статье Лодей, в особенности на c. 15».
79. Виро, 2012, с. 2.
80. Эндертон, 1977: «Эндертон называет это утверждение «Поглощающий закон арифметики кардинальных чисел»; оно зависит от сравнимости кардинальных чисел и, таким образом, от аксиомы выбора.».
81. Эндертон, 1977, с. 164.
82. Михалкин, 2009, с. 1.
83. Akian et al., 2006, p. 4.
84. Михалкин, 2009, с. 2.
85. Литвинов, 2005, с. 3.
86. Виро, 2012, с. 4.
87. Мартин, 2011, с. 49.
88. Стеварт, 2010, с. 8.

Литература

на русском языке

• Барсуков, А. Н. Алгебра : Учебник для VI—VIII классов / Под ред. С. И. Новосёлова. — М. : Просвещение, 1966. — 296 с.
• Выгодский, М. Я. Справочник по элементарной математике / М. Я. Выгодский. — М. : Астрель : АСТ, 2003. — 509 с. — ISBN 5-17-009554-6 (ООО Изд-во «АСТ»). — ISBN 5-271-02551-9 (ООО Изд-во «Астрель»).
• Гусев, В. А. Математика : Справ. материалы : Кн. для учащихся / В. А. Гусев, А. Г. Мордкович. — М. : Просвещение, 1988. — 476 с. — ISBN 5-09-001292-X.
• Зельвенский, И. Г. Группы, кольца, поля : Методич. указания по дисциплине «Геометрия и алгебра» / И. Г. Зельвенский. — СПб. : СПбГЭТУ, [б. г.]. — 30 с.
• Зубарева, И. И. Математика : 5 класс : учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 14-е изд., испр. и доп. — М. : Мнемозина, 2013. — 270 с. — ISBN 978-5-346-02573-3.
• Иванова О. А. Сложение // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 4 Ок—Сло. М.: «Советская Энциклопедия», 1984. 1216 стб., ил. Стб. 1212.
• Ильин, В. А. Математический анализ : Начальный курс / В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. — 2-е изд., пер. — М. : Изд-во Моск. ун-та, 1985. — 662 с.
• Истомина, Н. Б. Методика обучения математике в начальной школе : Развивающее обучение / Н. Б. Истомина. — 2-е изд. — Смоленск : Ассоциация XXI век, 2009. — 288 с. — ISBN 978-5-89308-699-7.
• Математика, её содержание, методы и значение : в 3 т. / [Ред. коллегия: чл.-кор. АН СССР А. Д. Александров и др.] ; Акад. наук СССР. Матем. ин-т им. В. А. Стеклова. — М. : Изд-во Акад. наук СССР, 1956. — Т. 3. — 336 с.
• Рудницкая, В. Н. Математика : 1 класс : учеб. для учащихся общеобразоват. учреждений. Второе полугодие / В. Н. Рудницкая. — 2-е изд., перераб. — М. : Вентана-Граф, 2004. — 111 с. — ISBN 5-88717-322-X (в пер.).
• Словарь русского языка : в 4 т. / РАН, Ин-т лингвистич. исследований ; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М. : Рус. яз. : Полиграфресурсы, 1999. — Т. 4. — 797 с. — ISBN 5-200-02672-5 («Русский язык»). — ISBN 5-87548-048-3 (Полиграфресурсы). — ISBN 5-200-02676-8 («Русский язык») (т. 4).
• Сложение // Большая советская энциклопедия. (В 30 томах) Гл. ред. А. М. Прохоров. Изд. 3-е. М.: «Советская энциклопедия», 1976. Т. 23. Сафлор — Соан. 1976. 639 с. с илл., 23 л. илл., 8 л. карт, 1 карта-вкладка. С. 583.
• Сложение // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 546.

на английском языке

• Akian, M. Min-plus methods in eigenvalue perturbation theory and generalised Lidskii-Vishik-Ljusternik theorem / M. Akian, R. Bapat, S. Gaubert. — 2006. — 16 February. — arXiv:math.SP/0402090v3.
• Austein, R. DATE-86, or The Ghost of Tinkles Past // The Risks Digest : journal. — 1987. — Vol. 4, no. 45.
• Baez, J. Mathematics Unlimited — 2001 and Beyond : From Finite Sets to Feynman Diagrams / J. Baez, J. Dolan. — Springer Berlin Heidelberg, 2000. — 1236 p. — ISBN 3-540-66913-2.
• Baroody, Arthur; Tiilikainen, Sirpa. Развитие арифметических понятий и навыков = The Development of Arithmetic Concepts and Skills. — Routledge, 2013. — 520 с. — ISBN 0-8058-3155-X.
• Begle, Edward. Математика в начальной школе = The Mathematics of the Elementary School. — McGraw-Hill, 1975. — 453 с. — ISBN 0-07-004325-6.
• Bergman, George. Приглашение к общей алгебре и универсальным конструкциям = An Invitation to General Algebra and Universal Constructions. — 2-е изд. — Springer, 2015. — 572 с. — ISBN 0-9655211-4-1.
• Joshua Bloch. Экстра, Экстра — Прочитать всё про Это: Почти все бинарные поиски сломаны (англ.) = Extra, Extra - Read All About It: Nearly All Binary Searches and Mergesorts are Broken // Official Google Research Blog : журнал. — 2006.
• Bogomolny, Alexander. Что такое сложение? (англ.) = What Is Addition?.
• Bates Bothman. Общая школьная арифметика = The common school arithmetic. — Prentice-Hall, 1837. — 270 с.
• Bunt, Lucas N. H.; Jones, Phillip S.; Bedient, Jack D. Исторические корни элементарной математики = The Historical roots of Elementary Mathematics. — Prentice-Hall, 2012. — 336 с. — ISBN 0-13-389015-5.
• Burrill, Claude. Основы действительных чисел = Foundations of Real Numbers. — McGraw-Hill, 1967. — 163 с.
• Beckmann, S. Изучение математики в начальной школе в целых числах (англ.) = The twenty-third ICMI study: primary mathematics study on whole numbers : журнал. — International Journal of STEM Education, 2014.
• Van de Walle, John. Математика в начальной и средней школе: развивающее обучение = Elementary and Middle School Mathematics: Teaching Developmentally. — 5-е изд. — Pearson Education, 2015. — 576 с. — ISBN 0-205-38689-X.
• Weaver, J. Fred. Сложение и вычитание: когнитивная точка зрения. Интерпретации числа операций и символических представлений сложения и вычитания = Addition and Subtraction: A Cognitive Perspective. Interpretations of Number Operations and Symbolic Representations of Addition and Subtraction. — Taylor & Francis, 2012. — С. 8. — ISBN 0-89859-171-6.
• Williams, Michael. История вычислительной техники = A History of Computing Technology. — Prentice-Hall, 1985. — ISBN 0-13-389917-9.
• Rebecca Wingard-Nelson. Десятичные и обыкновенные дроби: Это легко = Decimals and Fractions: It's Easy. — Enslow Publishers, 2014. — 64 с. — ISBN 0766042529.
• Wynn, Karen. Развитие математических навыков = The Development of Mathematical Skills. — Taylor & Francis, 1998. — 338 с. — ISBN 0-86377-816-X.
• Viro, Oleg; Cascuberta, Carles; Miró-Roig, Rosa Maria; Verdera, Joan; Xambó-Descamps, Sebastià, eds. Европейский конгресс математики: Барселона, Июль 10–14, 2000, Volume I = European Congress of Mathematics: Barcelona, July 10–14, 2000, Volume I. Dequantization of Real Algebraic Geometry on Logarithmic Paper. — Birkhäuser, 2012. — Т. 1. — 582 с. — ISBN 3-7643-6417-3.
• Henry, Valerie J.; Brown, Richard S. Изучение основных фактов первоклассниками = First-grade basic facts: An investigation into teaching and learning of an accelerated, high-demand memorization standard. — Heinemann, 2008.
• Dummit, D.; Foote, R. Абстрактная алгебра = Abstract Algebra. — Wiley, 1999. — 912 с.
• Davison, David M.; Landau, Marsha S.; McCracken, Leah; Thompson, Linda. Математика: Исследования и приложения = Mathematics: Explorations & Applications. — Prentice Hall. — ISBN 0-13-435817-1.
• Dale R. Patrick, Stephen W. Fardo, Vigyan Chandra. Основы Электронных Цифровых Систем = Electronic Digital System Fundamentals. — The Fairmont Press, 2008. — 340 с.
• Department of the Army (1961) Army Technical Manual TM 11-684. Принципы и Применения Математики для Межприборных соединений = Principles and Applications of Mathematics for Communications-electronics. — Headquarters, Department of the Army, 1992. — С. раздел 5.1. — 268 с.
• Devine, D.; Olson, J.; Olson, M. Элементарная математика для учителей = Elementary Mathematics for Teachers. — Wiley, 1991.
• Jackson, Albert. Аналоговые вычисления = Analog Computation. — McGraw-Hill, 1960.
• Johnson, Paul. От палок и камней: личные приключения в математике = From Sticks and Stones: Personal Adventures in Mathematics. — Science Research Associates, 1975. — 552 с. — ISBN 0-574-19115-1.
• Ifrah, Georges. Всеобщая история вычислительной техники: от абака до компьютера = The universal history of computing: from the abacus to the quantum computer. — John Wiley, 2001. — 410 с.
• Joshi, Kapil D. Основы дискретной математики = Foundations of Discrete Mathematics. — New Age International, 1989. — 748 с. — ISBN 978-0-470-21152-6.
• Dunham, William. Математическая Вселенная = The Mathematical Universe. — Wiley & Sons, 1994. — 314 с. — ISBN 0-471-53656-3.
• Kaplan, Robert. Что такое ничего: Естественная историю нуля = The Nothing That Is: A Natural History of Zero (англ.). — Oxford University Press, 1999. — 240 p. — ISBN 0-19-512842-7.
• Florian Cajori. История математических знаков = A History of Mathematical Notations. — The Open Court Company, 1928. — 818 с.
• Carpenter, Thomas; Fennema, Elizabeth; Franke, Megan Loef; Levi, Linda; Empson, Susan. Детская игровая математика = Children's Mathematics: Cognitively Guided Instruction. — Heinemann, 2014. — 218 с. — ISBN 0325052875.
• Karpinski, Louis. История арифметики = The history of arithmetic. — Russell & Russell, 1925. — 200 с.
• Килпатрик Д. Сложение: помощь детям в изучении математики = Adding It Up: Helping Children Learn Mathematics. — National Academy Press, 2001. — 454 с. — ISBN 0-309-06995-5.
• Conway, John B. Функция одной комплексной переменной = Functions of One Complex Variable I. — Springer Science, 1986. — 322 с. — ISBN 0-387-90328-3.
• Lee, John. Введение в гладкие многообразия = Introduction to Smooth Manifolds. — Springer, 2013. — 631 с. — ISBN 0-387-95448-1.
• Li, Y., & Lappan, G. Математический курс обучения в школьном образовании = Mathematics Curriculum in School Education. — Springer, 2013. — 663 с. — ISBN 9400775601.
• Linderholm, Carl. Математика затрудняет = Mathematics Made Difficult. — World Pub, 1972. — 207 с. — ISBN 0-7234-0415-1.
• Lipschutz, S., & Lipson, M. Схема Шаумся теории и проблем линейной алгебры = Schaum's Outline of Theory and Problems of Linear Algebra. — Erlangga, 2001. — 424 с. — ISBN 9797815714.
• Litvinov, Grigory; Maslov, Victor; Sobolevskii, Andreii. Иденпотентная математика и интервальный анализ = Idempotent mathematics and interval analysis. — American Mathematical Soc, 2005. — 370 с. — ISBN 0821835386.
• Jean-Louis Loday. Аритметр (англ.) = Arithmetree // Journal of Algebra : журнал. — 2002. — 22 декабря (№ 258). — doi:10.1016/S0021-8693(02)00510-0. — arXiv:math/0112034.
• Mazur, Joseph. Поучительные символы: Краткая История Математических Обозначений и их Скрытых Сил = Enlightening Symbols: A Short History of Mathematical Notation and Its Hidden Powers. — Princeton University Press, 2014. — 321 с. — ISBN 1400850118.
• Williams, Michael. История вычислительной техники = A History of Computing Technology. — 2. — IEEE Computer Society Press, 1997. — 426 с. — ISBN 0-13-389917-9.
• Marguin, Jean. История устройства вычислительных машин = Histoire des Instruments et Machines à Calculer, Trois Siècles de Mécanique Pensante 1642-1942. — Hermann., 1994. — 206 с. — ISBN 978-2-7056-6166-3.
• Mikhalkin, Grigory; Sanz-Solé, Marta, ed. Тропическая геометрия и её приложения = Tropical Geometry and its Applications. — 2-е изд. — Мадрин, Испания: Springer Science & Business Media, 2009. — 104 с. — ISBN 978-3-03719-022-7.
• Martin, John. Введение в языки и теорию вычислений = Introduction to Languages and the Theory of Computation. — 3. — McGraw-Hill, 2011. — 436 с. — ISBN 0-07-232200-4.
• Mosley, F. Использование цифровых линий с 5-8 летними детьми = Using Number Lines with 5-8 Year Olds. — Nelson Thornes, 2001. — 8 с. — ISBN 1874099952.
• Оксфордский словарь английского языка = Oxford English Dictionary (англ.). — Oxford University Press, 2005.
• Порядок выполнения операций (англ.) = Order of Operations Lessons // Algebrahelp : журнал. — 2012. Архивировано 2 ноября 2012 года.
• James Randerson. У слонов достаточно ума, чтобы рисовать фигуры (англ.) = Elephants have a head for figures : журнал. — Theguardian, 2008. — 21 августа.
• Riley, K.F.; Hobson, M.P.; Bence, S.J. Математические методы в физике и инженерии: полное руководство = Mathematical Methods for Physics and Engineering: A Comprehensive Guide. — Cambridge University Press, 2006. — 437 с. — ISBN 978-0-521-86153-3.
• Rudin, Walter. Основы математического анализа = Principles of Mathematical Analysis. — 3. — McGraw-Hill, 1976. — 342 с. — ISBN 0-07-054235-X.
• Yeo, Sang-Soo, et al., eds. Алгоритмы и архитектуры для параллельной обработки = Algorithms and Architectures for Parallel Processing. — Springer, 2010. — 574 с. — ISBN 3642131182.
• Smith, Karl. Природа современной математики = The Nature of Modern Mathematics. — 3-е изд. — Brooks/Cole Pub. Co., 1980. — 620 с. — ISBN 0-8185-0352-1.
• Smith, Frank. Стеклянная стена: почему математика может показаться трудной = The Glass Wall: Why Mathematics Can Seem Difficult. — Teachers College Press, 2002. — 163 с. — ISBN 0-8077-4242-2.
• Sparks, F.; Rees C. Исследование основной математики = A Survey of Basic Mathematics. — 4. — McGraw-Hill, 1979. — 543 с. — ISBN 0-07-059902-5.
• Stewart, James. Исчисление: раннее трансцендирование = Calculus: Early Transcendentals. — 4. — Brooks/Cole, 2010. — 1344 с. — ISBN 0-534-36298-2.
• Taton, René. Расчётная механика. Что я знаю? = Le Calcul Mécanique. Que Sais-Je ? n° 367 — Presses universitaires de France, 1963.
• Truitt, T.; Rogers, A. Основы аналоговых компьютеров = Basics of Analog Computers. — John F. Rider, 1960. — 378 с.
• Ferreirós, José. Лабиринты мысли: История теории множеств и её роль в современной математике = Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. — Birkhäuser, 2013. — 440 с. — ISBN 0-8176-5749-5.
• R. Fierro. Математика для учителей начальной школы = Mathematics for Elementary School Teachers. — Cengage Learning, 2012. — 976 с. — ISBN 0538493631.
• Flynn, M.; Oberman, S. Передовые компьютерные арифметические конструкции = Advanced Computer Arithmetic Design. — Wiley, 2001. — 325 с. — ISBN 0-471-41209-0.
• Fosnot, Catherine T.; Dolk, Maarten. Молодые математики за работой: Конструирование чувства числа, сложения и вычитания = Young Mathematicians at Work: Constructing Number Sense, Addition, and Subtraction. — Heinemann, 2001. — 193 с. — ISBN 0-325-00353-X.
• Hempel, C. G. Философия Карла Г. Хемптела: исследования в области науки, объяснения и рациональность = The philosophy of Carl G. Hempel: studies in science, explanation, and rationality (англ.). — Oxford University Press, 2000. — 464 p. — ISBN 0195343875.
• Horowitz, P.; Hill, W. Искусство схемотехники = The Art of Electronics. — 2. — Бином, 2009. — 704 с. — ISBN 0-521-37095-7.
• Schwartzman, Steven. Математические слова: Краткий Этимологический словарь математических терминов, используемых в английском языке = The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. — MAA, 1994. — 261 с. — ISBN 0-88385-511-9.
• Schmidt, W., Houang, R., & Cogan, L. Последовательность обучения (англ.) = A coherent curriculum : журнал. — American educator, 2002.
• Schyrlet Cameron, Carolyn Craig. Сложение и вычитание дробей в возрасте 5 — 8 лет = Adding and Subtracting Fractions, Grades 5 - 8. — Carson-Dellosa, 2013. — 64 с. — ISBN 162223006X.
• Schubert, E. Thomas; Phillip J. Windley; James Alves-Foss. Доказательство теорем логики более высоких порядков и их применение: труды 8-го международного фестиваля = Higher Order Logic Theorem Proving and Its Applications: Proceedings of the 8th International Workshop. — Springer, 1995. — 400 с.
• Enderton, Herbert. Элементы теории множеств = Elements of Set Theory. — Gulf Professional Publishing, 1977. — 279 с. — ISBN 0-12-238440-7.

Ссылки