Funkcja ciągła

Funkcja ciągła – funkcja, którą intuicyjnie można scharakteryzować jako:

1. funkcję, w której mała zmiana argumentu powoduje małą zmianę wartości funkcji; inaczej mówiąc, dla argumentów leżących blisko siebie wartości funkcji też leżą blisko,
2. funkcję rzeczywistą (określoną na zbiorze ${\displaystyle \mathbb {R} }$ lub jego podprzedziale), której wykresem jest ciągła linia, tj. linia narysowana bez odrywania ołówka od papieru.

Funkcja, która ma co najmniej jeden punkt nieciagłości, nazywana jest nieciagłą^[1]. Tzw. funkcja ze skokami po raz pierwszy została nazwana nieciagłą (ang. discontiguous) przez Arbogasta w 1791, który badał geometryczne rozwiązania równań różniczkowych^[2].

Ciągłość funkcji jest jednym z podstawowych pojęć topologii, gdzie jest definiowana w sposób najbardziej ogólny, rozszerzając pojęcie ciągłości funkcji zmiennych rzeczywistych oraz funkcji w przestrzeniach metrycznych. To ujęcie jest jednocześnie bardzo proste i pozwala jednolicie potraktować przypadki nieskończoności (bardzo potrzebne przy pojęciu granicy funkcji i granicy ciągu):

Zbiór ${\displaystyle X}$ staje się przestrzenią topologiczną, gdy dla każdego jego elementu określimy rodzinę otoczeń tego elementu – podzbiorów ${\displaystyle X.}$ Musi ona spełniać pewne warunki.

Najczęściej spotykamy się z takimi przestrzeniami topologicznymi, których topologia jest wyznaczona przez metrykę, czyli sposób określania odległości ${\displaystyle \rho (x,y)}$ punktów tej przestrzeni. Wtedy za otoczenia punktu przyjmuje się kule o środku w tym punkcie i dodatnim promieniu. Standardowo przyjmuje się kule otwarte, ale użycie kul domkniętych prowadzi do tej samej topologii. Natomiast gdyby dopuścić kule domknięte o promieniu 0, otrzymalibyśmy tzw. topologię dyskretną, na ogół inną od wprowadzonej przez metrykę.

Inaczej jest z nieskończonościami – tu nie określamy otoczeń przez metrykę: otoczeniami elementu ${\displaystyle +\infty }$ w rozszerzonym zbiorze liczb rzeczywistych są przedziały ${\displaystyle (M,+\infty ]}$ dla dowolnych ${\displaystyle M\in \mathbb {R}$ ;} otoczeniami elementu ${\displaystyle -\infty }$ są przedziały ${\displaystyle [-\infty ,M)}$ dla dowolnych ${\displaystyle M\in \mathbb {R} }$ (ciekawe są otoczenia ${\displaystyle -\infty }$ dla ${\displaystyle M<0}$).

Niech będą dane zbiory ${\displaystyle A}$ i ${\displaystyle B,}$ zawarte w przestrzeniach topologicznych, i funkcja ${\displaystyle f\colon A\to B.}$

Definicja (topologiczna): Funkcja ${\displaystyle f}$ jest ciągła w punkcie ${\displaystyle x_{0}\in A}$ jeśli

${\displaystyle \forall _{U{\text{ otoczenie }}f(x_{0})}\exists _{V{\text{ otoczenie }}x_{0}}\forall _{x\in V\cap A}:f(x)\in U,}$

symbole ${\displaystyle \forall }$ i ${\displaystyle \exists }$ to kwantyfikatory.

Definicja: Funkcja jest ciągła jeśli jest ciągła w każdym punkcie swojej dziedziny, czyli w zbiorze ${\displaystyle A.}$ Funkcja jest ciągła w zbiorze ${\displaystyle C}$ zawartym w jej dziedzinie jeśli jest ciągła w każdym punkcie tego zbioru.

W dalszym ciągu podajemy bardziej tradycyjne ujęcia i pokazujemy, że definicje Cauchy’ego są równoważne powyższym.

Ciągłość funkcji rzeczywistych zmiennej rzeczywistej

Dla funkcji rzeczywistych zmiennej rzeczywistej istnieją dwie równoważne definicje ciągłości^[3]:

• Cauchy’ego – podana przez Augustina Louisa Cauchy’ego^[4], nazywana też epsilonowo-deltową z racji używania liter ${\displaystyle \varepsilon }$ oraz ${\displaystyle \delta }$ w definicji;
• Heinego – podana przez Heinricha Eduarda Heinego, nazywana też definicją ciągową.

Niech ${\displaystyle M\subseteq \mathbb {R} }$ oraz ${\displaystyle f\colon M\to \mathbb {R} .}$

Definicje

Definicja Cauchy’ego

Funkcja ${\displaystyle f}$ jest ciągła w punkcie ${\displaystyle x_{0}\in M}$ wtedy i tylko wtedy gdy:

${\displaystyle \forall _{\varepsilon >0}\;\exists _{\delta >0}\;\forall _{x\in M}\ \ |x_{0}-x|<\delta \Rightarrow |f(x_{0})-f(x)|<\varepsilon .}$

Definicja ta jest równoważna topologicznej: warunek ${\displaystyle |x_{0}-x|<\delta }$ oznacza, że ${\displaystyle x}$ należy do kuli otwartej o środku ${\displaystyle x_{0}}$ i promieniu ${\displaystyle \delta }$ (czyli do otoczenia ${\displaystyle V}$). Warunek ${\displaystyle |f(x_{0})-f(x)|<\varepsilon }$ oznacza, że ${\displaystyle f(x)}$ należy do kuli otwartej o środku ${\displaystyle f(x_{0})}$ i promieniu ${\displaystyle \varepsilon }$ (czyli do otoczenia ${\displaystyle U}$). Tak więc zapis ${\displaystyle \forall _{\varepsilon >0}}$ oznacza wybranie otoczenia ${\displaystyle f(x_{0}),}$ a zapis ${\displaystyle \exists _{\delta >0}}$ oznacza dobranie do niego otoczenia ${\displaystyle x_{0}}$ (zamiast pisać ${\displaystyle \forall _{x\in V\cap A}}$ Cauchy pisze ${\displaystyle \forall _{x\in M}}$ (${\displaystyle M}$ pełni rolę ${\displaystyle A}$), a warunek przynależności do ${\displaystyle V}$ przenosi do poprzednika implikacji).

Definicja Heinego

Funkcja jest ciągła w punkcie ${\displaystyle x_{0}\in M,}$ wtedy i tylko wtedy, gdy dla każdego ciągu ${\displaystyle (x_{n})}$ liczb z ${\displaystyle M,}$ który jest zbieżny do ${\displaystyle x_{0},}$ ciąg wartości ${\displaystyle {\big (}f(x_{n}){\big )}}$ jest zbieżny do ${\displaystyle f(x_{0}),}$ czyli

${\displaystyle \forall _{(x_{n})\subset M}\ \ x_{n}\to x_{0}\Rightarrow f(x_{n})\to f(x_{0}),}$

Jeżeli funkcja ${\displaystyle f}$ spełnia jeden z powyższych warunków dla każdego ${\displaystyle x\in M,}$ to jest ona ciągła na zbiorze ${\displaystyle M}$ odpowiednio w sensie Cauchy’ego lub w sensie Heinego.

Mówimy, że funkcja jest ciągła, jeżeli jest ciągła na całej swojej dziedzinie.

Uwagi do definicji

Z obiema definicjami ciągłości funkcji w punkcie ściśle związane są odpowiednie definicje granicy funkcji w punkcie.

Zgodnie z powyższą definicją każda funkcja ${\displaystyle f}$ jest ciągła w punkcie izolowanym, tj. nie będącym punktem skupienia zbioru ${\displaystyle M.}$

Związanie z trzecim kwantyfikatorem we wzorze na ciągłość w sensie Cauchy’ego dwóch zmiennych z danego zbioru

${\displaystyle \forall _{\varepsilon >0}\;\exists _{\delta >0}\;\forall _{x_{1},x_{2}\in M}\;|x_{1}-x_{2}|<\delta \Rightarrow |f(x_{1})-f(x_{2})|<\varepsilon ,}$

prowadzi do sformułowania o wiele silniejszej własności, tzw. ciągłości jednostajnej^{[uwaga 1]}.

Obie definicje (Cauchy’ego i Heinego) są równoważne już przy założeniu bardzo słabej wersji aksjomatu wyboru, i nie jest on potrzebny dla dowodu równoważności globalnej ciągłości w odpowiednich znaczeniach.

Ciągłość jednostronna

Rozpatruje się czasami funkcje ciągłe jednostronnie: lewo- i prawostronne. Dla definicji Cauchy’ego należy dodać warunek dla ${\displaystyle x,}$ mianowicie ${\displaystyle x<x_{0},}$ aby otrzymać funkcję ciągłą lewostronnie. Definicja funkcji ciągłej prawostronnie wymaga zmiany powyższej nierówności na przeciwną. Definicja Heinego wymaga wybrania dowolnego ciągu zbliżającego się do ${\displaystyle x_{0}}$ wyłącznie punktami z lewej lub prawej strony.

Przykłady

Rozpatrujemy funkcje ${\displaystyle \cdot \colon \mathbb {R} \to \mathbb {R} .}$

• Wszystkie funkcje elementarne są ciągłe w swojej dziedzinie (co jest również prawdą dla funkcji ${\displaystyle \cdot \colon \mathbb {C} \to \mathbb {C} }$).
• Funkcja dana wzorem

${\displaystyle f(x)={\begin{cases}{\tfrac {\sin x}{x}}&{\text{dla }}x\neq 0\\[2pt]\;1&{\text{dla }}x=0\end{cases}}}$

jest ciągła.

• Funkcja skokowa Heaviside’a jest ciągła prawie wszędzie – we wszystkich punktach dziedziny poza zerem: ${\displaystyle \mathbb {R} \setminus \{0\}.}$
• Funkcja Dirichleta ${\displaystyle D}$ jest nigdzie ciągła (tzn. nie jest ciągła w żadnym punkcie swojej dziedziny).
  • Funkcja ${\displaystyle D_{1}(x)=x\cdot D(x)}$ jest ciągła wyłącznie w punkcie ${\displaystyle x=0.}$
  • Funkcja ${\displaystyle D_{\mathbb {Z} }=\sin(x\pi )\cdot D(x)}$ jest ciągła we wszystkich całkowitych punktach dziedziny.
• Funkcja Riemanna ${\displaystyle R}$ jest ciągła we wszystkich niewymiernych i nieciągła we wszystkich wymiernych punktach dziedziny.

Własności

• Złożenie funkcji ciągłych jest funkcją ciągłą.
• Jeżeli funkcja rzeczywista, której dziedziną jest przedział domknięty, jest ciągła, ${\displaystyle f\colon [a,b]\to \mathbb {R} ,}$ to na dziedzinie:

1. jest jednostajnie ciągła,
2. przyjmuje swoje ekstrema (zob. twierdzenie Weierstrassa o kresach),
3. ma własność Darboux (zob. twierdzenie Darboux).

Ciągłość funkcji w przestrzeniach metrycznych i unormowanych

Definicje

W przestrzeniach metrycznych i przestrzeniach unormowanych stosuje się nieznacznie tylko zmodyfikowane wersje definicji Cauchy’ego, zastępując każdą wartość bezwzględną różnicy odpowiednią dla każdej przestrzeni metryką lub normą różnicy.

Dla przestrzeni metrycznych ${\displaystyle (X,d_{X})}$ oraz ${\displaystyle (Y,d_{Y})}$ funkcja ${\displaystyle f\colon X\to Y}$ jest ciągła w punkcie ${\displaystyle x_{0}\in X,}$ jeśli prawdziwe jest zdanie

${\displaystyle \forall _{\varepsilon >0}\;\exists _{\delta >0}\;\forall _{x\in X}\;d_{X}(x_{0},x)<\delta \Rightarrow d_{Y}(f(x_{0}),f(x))<\varepsilon .}$

Powyższą implikację można zapisać również w postaci

${\displaystyle \forall _{\varepsilon >0}\;\exists _{\delta >0}\;f(B_{X}(x_{0},\delta ))\subseteq B_{Y}(f(x_{0}),\varepsilon )}$ albo ${\displaystyle \forall _{\varepsilon >0}\;\exists _{\delta >0}\;B_{X}(x_{0},\delta )\subseteq f^{-1}{\big (}B_{Y}(f(x_{0}),\varepsilon ){\big )},}$

gdzie ${\displaystyle B_{X},\ B_{Y}}$ oznaczają kule otwarte odpowiednio w ${\displaystyle X}$ oraz ${\displaystyle Y;}$ ${\displaystyle x_{0},\delta }$ oznaczają środek i promień kuli ${\displaystyle B_{X}}$ (analogicznie jest dla kuli ${\displaystyle B_{Y}}$).

Odpowiednikiem definicji ciągłości funkcji ${\displaystyle f\colon X\to Y}$ w sensie Heinego jest:

${\displaystyle \forall _{(x_{n})\subset X}\ \ d_{X}(x_{n},x_{0})\to 0\Rightarrow d_{Y}(f(x_{n}),f(x_{0}))\to 0.}$

Przykłady

• Dwuargumentowe działania algebraiczne ${\displaystyle \mathbb {C} ^{2}\to \mathbb {C} }$ zdefiniowane ${\displaystyle f(a,b)=a+b,\ g(a,b)=ab}$ dla ${\displaystyle a,b\in \mathbb {C} .}$
  Zbiór liczb zespolonych ${\displaystyle \mathbb {C} }$ jest przestrzenią metryczną w metryką ${\displaystyle d_{\mathbb {C} }(a,b)=|a-b|,}$
  zbiór par liczb zespolonych ${\displaystyle \mathbb {C} ^{2}}$ jest przestrzenią metryczną w metryką ${\displaystyle d_{\mathbb {C} }((a,b),(c,d))=\max(|a-c|,|b-d|),}$
  gdzie ${\displaystyle |.|}$ oznacza moduł liczby zespolonej.
• Jednoargumentowe działanie algebraiczne ${\displaystyle \mathbb {C} \to \mathbb {C} }$ zdefiniowane ${\displaystyle f(a)=a^{-1}}$ dla ${\displaystyle a\in \mathbb {C} \setminus \{0\}.}$
• Jednoargumentowe działanie ${\displaystyle \mathbb {C} \to \mathbb {C} }$ zdefiniowane ${\displaystyle f(a)={\overline {a}}}$ dla ${\displaystyle a\in \mathbb {C} .}$
• Metryka naturalna ${\displaystyle S^{n}\times S^{n}\to \mathbb {R} }$ na sferze ${\displaystyle S^{n},}$ zdefiniowana formalnie jako ${\displaystyle d_{S^{n}}(a,b)=\arccos \left({\tfrac {\mathbf {a} \cdot \mathbf {b} }{\|\mathbf {a} \|\|\mathbf {b} \|}}\right),}$ czyli jako kąt między niezerowymi wektorami ${\displaystyle a,b\in E^{n+1}}$

Ciągłość funkcji w przestrzeniach topologicznych

Definicja

Ciągłość funkcji w punkcie ${\displaystyle x{:}}$ dla otoczenia ${\displaystyle V}$ punktu ${\displaystyle f(x)}$ możemy znaleźć otoczenie ${\displaystyle U}$ punktu ${\displaystyle x}$ takie, że ${\displaystyle f(U)}$ jest zawarte w ${\displaystyle V.}$

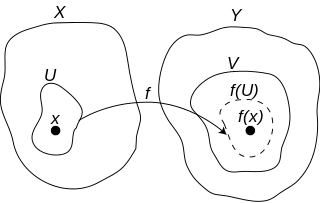
Najpełniejszą oraz najogólniejszą definicję ciągłości wprowadza się w topologii^[5].

Niech ${\displaystyle (X,\tau _{X})}$ oraz ${\displaystyle (Y,\tau _{Y})}$ będą przestrzeniami topologicznymi.

Mówimy, że funkcja ${\displaystyle f\colon X\to Y}$ jest ciągła w punkcie ${\displaystyle x\in X,}$ jeżeli dla każdego otoczenia ${\displaystyle V\subseteq Y}$ punktu ${\displaystyle f(x)}$ istnieje otoczenie ${\displaystyle U}$ punktu ${\displaystyle x}$ takie, że jego obraz ${\displaystyle f(U)}$ zawiera się w ${\displaystyle V}$ (patrz rysunek obok).

Jeśli przestrzenie ${\displaystyle X,\ Y}$ są metryzowalne, to powyższa definicja zgadza się z definicją ciągłości w sensie Cauchy’ego podaną wyżej.

Badanie ciągłości funkcji między przestrzeniami topologicznymi

W topologii często bada się przestrzeń, której elementami są funkcje ciągłe z jednej przestrzeni topologicznej w inną. Niech ${\displaystyle (X,\tau _{X})}$ i ${\displaystyle (Y,\tau _{Y})}$ będą przestrzeniami topologicznymi oraz ${\displaystyle f\colon X\to Y.}$

Aby sprawdzić ciągłość funkcji ${\displaystyle f,}$ nie trzeba badać wszystkich elementów topologii danej przestrzeni.

• Można zbadać dla pewnej bazy ${\displaystyle {\mathcal {B}}}$ tej przestrzeni: funkcja ${\displaystyle f}$ jest ciągła wtedy i tylko wtedy, gdy przeciwobraz każdego zbioru otwartego ${\displaystyle U\in {\mathcal {B}}}$ jest otwarty, tj. należy do topologii ${\displaystyle f^{-1}(U)\in \tau _{X}.}$
• Ciągłość można także badać za pomocą zbiorów domkniętych. Mianowicie, funkcja ${\displaystyle f}$ jest ciągła wtedy i tylko wtedy, gdy zachodzi jakikolwiek z następujących warunków:
  • przeciwobraz dowolnego zbioru domkniętego w ${\displaystyle Y}$ jest domknięty w ${\displaystyle X;}$
  • dla każdego zbioru ${\displaystyle A\subseteq X}$ spełniony jest warunek
    ${\displaystyle f(\operatorname {cl} \;A)\subseteq \operatorname {cl} \;f(A),}$
    gdzie ${\displaystyle \operatorname {cl} \;A}$ oznacza domknięcie zbioru ${\displaystyle A;}$
  • dla każdego zbioru ${\displaystyle B\subseteq Y}$ spełniony jest warunek

${\displaystyle \operatorname {cl} \;f^{-1}(B)\subseteq f^{-1}(\operatorname {cl} \;B).}$

Każda z poniższych własności jest zachowywana przez obrazy funkcji ciągłej, tzn. jeżeli ${\displaystyle f\colon X\to Y}$ jest funkcją ciągłą oraz ${\displaystyle X}$ ma jedną z poniższych własności, to ma ją również obraz ${\displaystyle f(X){:}}$

• zwartość,
• ośrodkowość,
• spójność.

Jeśli zbiór ${\displaystyle D}$ jest gęsty w ${\displaystyle X,}$ a ${\displaystyle f,g\colon X\to Y}$ są ciągłe oraz ${\displaystyle f(x)=g(x)}$ dla każdego ${\displaystyle x\in D,}$ to ${\displaystyle f=g.}$

Przestrzeń funkcji ciągłych między przestrzeniami topologicznymi

Przestrzeń, której elementami są funkcje ciągłe z przestrzeni topologicznej ${\displaystyle X}$ w inną przestrzeń ${\displaystyle Y}$ jest oznaczana symbolem ${\displaystyle {\mathcal {C}}(X,Y).}$ Przestrzeń ta jest szczególnym przypadkiem przestrzeni funkcyjnej.

Jednym z najbardziej popularnych przykładów są przestrzenie funkcji ciągłych o wartościach w liczbach rzeczywistych. Pierścień ${\displaystyle {\mathcal {C}}(X,\mathbb {R} )}$ o elementach będących odwzorowaniami ciągłymi z ${\displaystyle X}$ w ${\displaystyle \mathbb {R} }$ i operacjach algebraicznych wprowadzanych „punktowo” jest ważnym obiektem topologicznym. Przeprowadzono wiele badań w poszukiwaniu związków struktury algebraicznej tego pierścienia ze strukturą topologiczną przestrzeni ${\displaystyle (X,\tau _{X}).}$

Na przestrzeni ${\displaystyle {\mathcal {C}}(X,\mathbb {R} )}$ rozważa się także strukturę topologiczną, wprowadzając topologie:

zbieżności punktowej

zgodną z topologią Tichonowa na iloczynie ${\displaystyle \prod _{x\in X}~\mathbb {R}$ ;}

zbieżności jednostajnej

w której bazą otoczeń punktu ${\displaystyle f\in {\mathcal {C}}(X)}$ jest ${\displaystyle \{U_{n}(f)\colon \ n=1,2,3,\dots \},}$ gdzie ${\displaystyle U_{n}(f)=\left\{g\in {\mathcal {C}}(X)\colon \ \forall _{x\in X}\;|f(x)-g(x)|<{\tfrac {1}{n}}\right\}.}$

Ciągłość funkcji w terminach teoriomnogościowych

Niech ${\displaystyle (A,\leqslant _{A})}$ oraz ${\displaystyle (B,\leqslant _{B})}$ będą porządkami zupełnymi.

Funkcja ${\displaystyle f\colon A\to B}$ jest ciągła, jeżeli zachowuje kresy górne podzbiorów skierowanych, tzn. dla dowolnego podzbioru skierowanego ${\displaystyle X\subseteq A}$ zachodzi ${\displaystyle f(\sup X)=\sup f(X).}$

Zobacz też

• funkcja jednostajnie ciągła
• funkcja różniczkowalna
• punkt odosobniony
• warunek Höldera
• warunek Lipschitza

Uwagi

1. Należy zwracać bacznie uwagę na kolejność kwantyfikatorów we wzorach:

   ${\displaystyle \forall _{x_{0}\in M}\;\forall _{\varepsilon >0}\;\exists _{\delta >0}\;\forall _{x\in M}\;|x_{0}-x|<\delta \Rightarrow |f(x_{0})-f(x)|<\varepsilon ,}$

   ${\displaystyle \forall _{\varepsilon >0}\;\exists _{\delta >0}\;\forall _{x_{0}\in M}\;\forall _{x\in M}\;|x_{0}-x|<\delta \Rightarrow |f(x_{0})-f(x)|<\varepsilon ,}$

   Pierwszy z nich stwierdza ciągłość funkcji w sensie Cauchy’ego na zbiorze ${\displaystyle M,}$ drugi stwierdza jednostajną ciągłość funkcji na zbiorze ${\displaystyle M.}$

Przypisy

1. funkcja nieciągła, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2024-03-13].
2. Jahnke 2003 ↓, s. 165.
3. funkcja ciągła, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2023-02-07].
4. Jahnke 2003 ↓, s. 161.
5. Trajdos 1993 ↓, s. 332.

Bibliografia

• T. Trajdos: Matematyka. Cz. III. Warszawa: Wydawnictwa Naukowo-Techniczne, 1993, seria: Podręczniki akademickie.
• Hans Niels Jahnke: A history of analysis. Providence, RI: American Mathematical Society, 2003. ISBN 0-8218-2623-9. OCLC 51607350.

Literatura dodatkowa

• Ryszard Engelking: Topologia ogólna, Warszawa: Państwowe Wydawnictwo Naukowe, 1976.
• Witold Kołodziej, Analiza matematyczna, Warszawa: Wydawnictwo Naukowe PWN, 2009.
• Kazimierz Kuratowski: Wstęp do teorii mnogości i topologii. Wyd. 4, Warszawa: PWN, 1966.

Linki zewnętrzne

• MartaM. Szumańska MartaM., Ciągłość, „Delta”, kwiecień 2019, ISSN 0137-3005 [dostęp 2022-07-19].
• Eric W.E.W. Weisstein Eric W.E.W., Continuous Function, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2023-02-07].
• Continuous function (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-02-07].
• William L. Hosch, continuity (ang.), Britannica Online, 18 stycznia 2023 [dostęp 2023-02-07].

Kontrola autorytatywna (rodzaj funkcji matematycznej):

• LCCN: sh85052334
• GND: 4183162-7
• BnF: 12123565q
• BNCF: 53874
• J9U: 987007553158805171
• LNB: 000193599

Encyklopedie internetowe:

• Britannica: topic/continuous-function
• Universalis: continuite-mathematique
• Catalana: 0153274
• DSDE: kontinuitet