Przedział (matematyka)

Przedział – typ podzbioru w zbiorze częściowo uporządkowanym, zdefiniowany odpowiednimi nierównościami; elementy przedziału są zawarte między dwoma ustalonymi elementami, nazywanymi początkiem i końcem przedziału. Podstawowe przykłady to przedziały liczbowe – podzbiory liczb rzeczywistych wyposażonych w standardowy porządek^[1]: ${\displaystyle (\mathbb {R} ,\leq ).}$

Zobacz też: inne znaczenia słowa „przedział”.

Przykładowe przedziały liczbowe – spójne podzbiory osi rzeczywistej; kolejno przedział otwarty, domknięty i dwa półotwarte; wszystkie cztery są ograniczone.

Prosta, półprosta i odcinek – jednowymiarowe figury geometryczne odpowiadające niektórym rodzajom przedziałów liczbowych

Całkę Riemanna definiuje się przez podział dziedziny funkcji na przedziały.

Wyróżnia się różne typy przedziałów:

• ograniczone lub nie^[2];
• otwarte, domknięte lub otwarte jednostronnie, zwane też jednostronnie domkniętymi^[1], półotwartymi lub półdomkniętymi^{[potrzebny przypis]}.

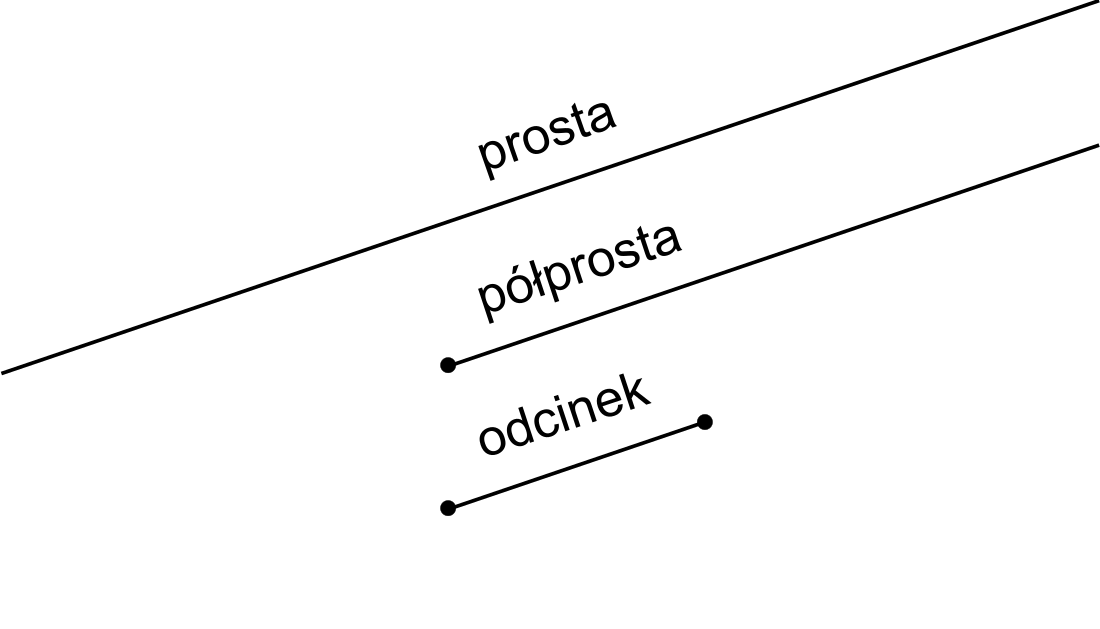
Niektóre przedziały liczbowe można utożsamiać z podstawowymi, jednowymiarowymi figurami geometrycznymi:

• zbiór wszystkich liczb rzeczywistych to prosta;
• przedziały nieograniczone domknięte (jednostronnie) to półproste;
• przedziały ograniczone domknięte (obustronnie) to odcinki.

Przedziały, zwłaszcza te liczbowe, są używane w różnych działach matematyki i innych naukach, co opisano dalej.

Definicje formalne

Niech ${\displaystyle (X,\leqslant )}$ będzie zbiorem częściowo uporządkowanym i niech ${\displaystyle x,y\in X}$ oraz ${\displaystyle x\leqslant y.}$

Przedziałem wyznaczonym przez ${\displaystyle x,y}$ jest jeden z następujących zbiorów:

• ${\displaystyle (x,y):=\{z\in X:x<z<y\}}$ – przedział (obustronnie) otwarty,
• ${\displaystyle [x,y):=\{z\in X:x\leqslant z<y\}}$ – przedział lewostronnie domknięty (prawostronnie otwarty),
• ${\displaystyle [x,y]:=\{z\in X:x\leqslant z\leqslant y\}}$ – przedział (obustronnie) domknięty,
• ${\displaystyle (x,y]:=\{z\in X:x<z\leqslant y\}}$ – przedział prawostronnie domknięty (lewostronnie otwarty).

Ponadto

• ${\displaystyle (-\infty ,y):=\{z\in X:z<y\}}$ – przedział lewostronnie nieograniczony, prawostronnie otwarty,
• ${\displaystyle (-\infty ,y]:=\{z\in X:z\leqslant y\}}$ – przedział lewostronnie nieograniczony, prawostronnie domknięty,
• ${\displaystyle (x,+\infty ):=\{z\in X:x<z\}}$ – przedział prawostronnie nieograniczony, lewostronnie otwarty,
• ${\displaystyle [x,+\infty ):=\{z\in X:x\leqslant z\}}$ – przedział prawostronnie nieograniczony, lewostronnie domknięty.

Jeśli w zbiorze uporządkowanym ${\displaystyle (X,\leqslant )}$ istnieje element największy, to definicja przedziału prawostronnie nieograniczonego jest zbędna; jeśli istnieje element najmniejszy, to definicja przedziału lewostronnie nieograniczonego jest zbędna.

Dla pełności należy dodać jeszcze następujące dwie definicje:

• ${\displaystyle (\infty ,\infty ):=\{z\in X\}=X}$ – przedział obustronnie nieograniczony, czyli cały zbiór ${\displaystyle (X,\leqslant ).}$
• ${\displaystyle \varnothing }$ – przedział pusty, czyli przedział niezawierający żadnego elementu; takim przedziałem są np. ${\displaystyle (x,x),\;(x,x],\;[x,x).}$

Oznaczenia

Niektórzy autorzy używają oznaczeń ${\displaystyle (x,y)_{X},}$ ${\displaystyle [x,y]_{X}}$ itp. dla podkreślenia, że rozpatrywane są przedziały w danym porządku.

Często zamiast ${\displaystyle [x,y]}$ stosuje się oznaczenie ${\displaystyle \langle x,y\rangle }$ i analogicznie dla przedziałów jednostronnie domkniętych^[2]. Należy jednak zwrócić uwagę, że zarówno ${\displaystyle (x,y),}$ jak i ${\displaystyle \langle x,y\rangle }$ do oznaczenia przedziałów mogą być pomylone z podobnymi notacjami używanymi do oznaczenia par uporządkowanych.

Norma międzynarodowa ISO31-11 przewiduje zamiast oznaczeń ${\displaystyle (x,y],[x,y),(x,y)}$ dla przedziałów lewo- i prawo- lub obustronnie otwartych stosowanie następujących oznaczeń ${\displaystyle ]x,y],\ [x,y[,\ ]x,y[.}$

Stosowanie średnika lub przecinka wynika z zastosowanej konwencji dla separatora dziesiętnego.

Przykłady

• Przedziały liczbowe:
  • ${\displaystyle (0,1)}$ – zbiór wszystkich dodatnich liczb rzeczywistych mniejszych niż ${\displaystyle 1,}$
  • ${\displaystyle [2,e)}$ – zbiór liczb rzeczywistych większych lub równych ${\displaystyle 2,}$ ale mniejszych niż ${\displaystyle e,}$
  • przedział nieskończony ${\displaystyle (\pi ,\infty )}$ złożony z wszystkich liczb większych niż ${\displaystyle \pi ,}$
  • ${\displaystyle (0,0),\ (7,7],\ [2,2)}$ – przedziały puste,
  • ${\displaystyle [4,4]}$ – przedział jednopunktowy ${\displaystyle \{4\}.}$

• Przedziały zależą od porządków, w których są rozważane: ${\displaystyle (-5,5)_{\mathbb {Z} }}$ jest zbiorem skończonym (jest to ${\displaystyle \{-4,-3,-2,-1,0,1,2,3,4\}}$), ale ${\displaystyle (-5,5)_{\mathbb {Q} }}$ jest zbiorem nieskończonym (jest to zbiór wszystkich liczb wymiernych większych od –5 a mniejszych niż 5). Zwyczajowo, przedział ${\displaystyle (a,b]}$ pomiędzy liczbami rzeczywistymi ${\displaystyle a,b\in \mathbb {R} }$ oznacza przedzial w liczbach rzeczywistych, tzn. ${\displaystyle (a,b]_{\mathbb {R} },}$ podobnie dla innych przedziałów.

• Rozważmy płaszczyznę ${\displaystyle \mathbb {R} ^{2}}$ z porządkiem częściowym zdefiniowanym przez ${\displaystyle \langle x_{1},y_{1}\rangle <\langle x_{2},y_{2}\rangle \iff x_{1}\leqslant x_{2}}$ i ${\displaystyle y_{1}\leqslant y_{2},}$ gdzie relacja ${\displaystyle \leqslant }$ jest naturalnym porządkiem na prostej ${\displaystyle \mathbb {R} .}$ Wówczas przedział domknięty ${\displaystyle {\big [}\langle 0,0\rangle ,\langle 1,1\rangle {\big ]}_{\mathbb {R} ^{2}}}$ jest domkniętym kwadratem o wierzchołkach w ${\displaystyle \langle 0,0\rangle ,\langle 0,1\rangle ,\langle 1,0\rangle ,\langle 1,1\rangle ,}$ tzn. zbiorem ${\displaystyle \left\{\langle x,y\rangle \in \mathbb {R} ^{2}:0\leqslant x\leqslant 1\ \land \ 0\leqslant y\leqslant 1\right\}.}$

Własności

Suma mnogościowa dwóch przedziałów może nie być przedziałem.

Suma mnogościowa dwóch przedziałów może również być przedziałem; warunkiem wystarczającym na to jest, by miały niepusty przekrój. Nie jest to jednak warunek konieczny – przedziały liczb nieujemnych oraz ujemnych są rozłączne, jednak ich suma mnogościowa – cała oś rzeczywista – jest przedziałem.

Przekrój (przecięcie) dwóch przedziałów zawsze jest przedziałem. Innymi słowy zbiór wszystkich przedziałów liczbowych z działaniem przekroju tworzy monoid, gdzie elementem neutralnym jest cała oś rzeczywista^{[potrzebny przypis]}. Ten typ monoidów – gdzie każdy element jest idempotentny – zalicza się do pasów.

Wprawdzie definicja przedziału jest poprawna dla dowolnego porządku częściowego, to jednak w praktyce matematycznej przedziały najczęściej rozpatruje się w porządkach liniowych.

Niech ${\displaystyle (X,\leqslant )}$ będzie porządkiem liniowym.

• Część wspólna dwóch przedziałów jest przedziałem.
• Dopełnienie przedziału jest albo przedziałem, albo sumą dwóch przedziałów.
• Suma dwóch przedziałów o niepustej części wspólnej jest przedziałem.
• Otwarte przedziały w ${\displaystyle X}$ tworzą bazę pewnej topologii na ${\displaystyle X}$ – ta topologia nazywana jest topologią przedziałową na ${\displaystyle X}$ albo topologią porządkową na ${\displaystyle X}$.
• Topologia porządkowa na zbiorze liczb rzeczywistych jest naturalną topologią na ${\displaystyle \mathbb {R} .}$ Bazę tej topologii tworzą przedziały otwarte o końcach wymiernych.

Każdy przedział liczbowy otwarty jest jednocześnie zbiorem otwartym w sensie topologii; podobnie przedziały domknięte należą do zbiorów domkniętych. Zbiór pusty oraz cała oś rzeczywista można zaliczyć do przedziałów otwartych lub półotwartych i są one zbiorami zbiorami otwarto-domkniętymi. Inne przedziały półotwarte nie są ani zbiorami otwartymi, ani domkniętymi^{[potrzebny przypis]}. Przedziały liczbowe są tym samym, co zbiory spójne na osi rzeczywistej.

Rola

Matematyka

• Za pomocą przedziałów i działania sumy zbiorów można opisać zbiory rozwiązań przynajmniej części równań i nierówności liczbowych, a także dziedziny często używanych funkcji zmiennej rzeczywistej, np. tych elementarnych^{[potrzebny przypis]};
• badanie przebiegu zmienności funkcji polega m.in. na wskazaniu przedziałów o określonym znaku wartości oraz o określonej monotoniczności i wypukłości lub wklęsłości;
• za pomocą przedziałów można zdefiniować pewne pojęcia analizy matematycznej jak własność Darboux czy całka Riemanna;
• przedziały są też jednym z fundamentów topologii; dostarczają podstawowych przykładów różnych typów zbiorów wyróżnianych przez tę naukę – otwartych, domkniętych, otwarto-domkniętych, spójnych, obszarów i continuów;
• zbiory przedziałów tworzą różne struktury algebraiczne, przykładowo z działaniem przekroju zbiorów, a w przypadku przedziałów liczbowych – z dodawaniem Minkowskiego i iloczynem kompleksowym;
• pojęcie przedziału pojawia się też w definicji prawdopodobieństwa jako miary o wartościach w przedziale jednostkowym;
• analiza numeryczna celuje m.in. w znajdowanie przedziałów, w których znajdują się rozwiązania pewnych równań liczbowych;
• przedziały liczb wymiernych pojawiają się też w jednej z definicji konstrukcyjnych liczb rzeczywistych – przez przekroje Dedekinda;

Za pomocą przedziałów liczbowych i iloczynu kartezjańskiego można zdefiniować prostokąt, prostopadłościan i ich uogólnienia zwane przedziałami wielowymiarowymi. W topologii rozważa się też ich odpowiedniki oparte na nieskończonych iloczynach kartezjańskich, znane jako kostki Tichonowa. Inne odpowiedniki przedziałów w wyższych wymiarach to koła i kule – te ostatnie definiuje się w dowolnych przestrzeniach metrycznych.

Inne nauki

Nauki empiryczne jak fizyka, astronomia i geodezja posługują się przedziałami liczbowymi, ponieważ to one – a nie pojedyncze liczby – są wynikami pomiarów, zawsze ograniczonych niepewnością.

Zobacz też

Zobacz hasło przedział w Wikisłowniku

• otoczenie i sąsiedztwo
• zakres (programowanie)
• zbiór borelowski
• analiza przedziałowa

Przypisy

1. przedział liczbowy, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2023-08-19].
2. Przedziały liczbowe. Przedziały jako zbiory, Zintegrowana Platforma Edukacyjna, zpe.gov.pl [dostęp 2024-06-21].

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Interval, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2023-08-19].
• Interval and segment (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org [dostęp 2023-08-19].

Encyklopedie internetowe (order-convex set):

• SNL: intervall_-_matematikk