Cercle

En géométrie euclidienne, un cercle est une courbe plane fermée constituée de points situés à égale distance d'un point nommé centre. Cette distance est appelée rayon du cercle.

Cercle
Représentation d'un cercle Circonférence C Diamètre D Rayon R Centre ou Origine O
Type	Section conique
Groupe de symétrie	O(2)
Aire	πR2
Périmètre	C = 2πR
Propriétés	Constructible
modifier

Le cercle de centre M et de rayon r est l'ensemble des points du plan à distance r de M.

Dans le plan euclidien, il s'agit du « rond » qui est associé en français au terme de cercle. Dans un plan non euclidien ou dans le cas de la définition d'une distance non euclidienne, la forme peut être plus complexe. Dans un espace de dimension quelconque, l'ensemble des points placés à une distance constante d'un centre est appelé sphère.

D'autres formes peuvent être qualifiées de « rondes » : les surfaces et solides dont certaines sections planes sont des cercles (cylindres, cônes, tore, anneau, etc.)^[1].

Utilisations

Le cercle est un objet mathématique abstrait, qui peut servir à modéliser de nombreux phénomènes. Un certain nombre d'objets manufacturés ont une section circulaire : cylindres (rouleaux, roues, silos), sphères (ballon, balles, billes), cônes (rouleaux, entonnoirs). Les propriétés du cercle permettent donc de déduire des propriétés des objets, comme leur volume qui permet de déduire la masse de l'objet (connaissant sa masse volumique) ou sa contenance. Les objets de section circulaire sont intéressants pour principalement plusieurs raisons :

• ces objets roulent, ce qui permet d'avoir des mouvements et déplacements nécessitant peu d'efforts (roues, roulements mécaniques) ;
• par définition, tous les points sont à égale distance du centre ; cela signifie qu'il faut le même temps et la même énergie pour atteindre chaque point à partir du centre, ce qui a donné la notion d'hémicycle (amphithéâtre) dans lequel le son a le même volume pour tous ceux assis sur le même banc.
  Cela a également de l'importance en termes d'organisation du territoire et de logistique ; en effet, si le déplacement se fait de la même manière dans toutes les directions (terrain idéalement plat et horizontal, sans obstacle, ou bien vol d'oiseau sans vent), alors un cercle représente l'ensemble des points que l'on peut atteindre pour une durée de trajet donnée ou une consommation d'énergie donnée à partir du centre, c'est la notion de rayon d'action, et l'intérêt du problème du cercle minimum ;
  lorsque l'on souffle du verre, le verre s'éloigne du point de soufflage avec une vitesse isotrope, ce qui donne à l'objet une forme naturellement arrondie ;
• le cercle est la courbe plane qui, pour une longueur donnée (périmètre), a l'aire la plus grande. En particulier, le disque, dont la frontière est un cercle, correspond au cas d'égalité de l'inégalité isopérimétrique en dimension 2 (pour plus de détails, consulter Théorème isopérimétrique). Ainsi, si l'on construit un silo ou une bouteille cylindrique, on a la contenance la plus importante pour une quantité de matériau donné (pour faire la paroi), si l'on construit une palissade circulaire, on pourra loger plus de personnes pour une quantité de bois ou de pierre donnée ; dans le même ordre d'idées, la défense en cercle est une stratégie militaire permettant de défendre une population ou un stock avec le minimum de moyens, face à une attaque venant de toutes parts, tactique dite justement de l'encerclement.
• cette forme ne présente pas d'aspérité, donc pas de concentration de contrainte ; un objet ayant cette forme a une meilleure résistance mécanique ;
• cette forme ne présente pas de partie plane, ainsi, un projectile a peu de chance de la frapper « de face », il lui transmet moins d'énergie, et donc risque moins de l'endommager ; si l'objet tombe, il a plus de chance de rebondir sans casser ; un objet arrondi a aussi moins de risque de blesser en cas de choc avec une personne (ballon, arrondi des capots et pare-chocs de voitures modernes) ;
• toute droite passant par le centre est un rayon, et donc est perpendiculaire au cercle ; cette propriété est utilisée en optique et a donné les contre-miroirs sphériques, c'est aussi pour cela que les lentilles ont des surfaces sphériques (on peut facilement prédire le trajet lumineux aux dioptres) ;
• un objet de section circulaire et à paroi mince peut se fabriquer par enroulement de fil (ressort hélicoïdal, bobine) ou par roulage d'une tôle (virole, tube) ; un objet de section circulaire creux ou massif peut aussi s'obtenir facilement par tournage (poterie, tournage mécanique) ;
• si l'on met un objet dans un récipient circulaire, on impose sa position mais on n'impose pas son orientation ; si l'orientation n'a pas d'importance, alors cela permet de gagner du temps puisque l'on n'a pas à tourner l'objet avant de le mettre en position ; c'est le principe du centrage (long ou court) pour la mise en position (MiP).

Certains objets répondent à plusieurs de ces éléments. Par exemple, le fait qu'un canon soit cylindrique :

• permet une fabrication facile, en particulier l'alésage ;
• donne une résistance mécanique (résistance à la pression de l'explosion) ;
• facilite l'introduction de la munition (on n'a pas besoin de la tourner autour de son axe pour l'introduire) ;
• en pratiquant une hélice dans le canon, on peut imprimer un mouvement de rotation lors du tir qui stabilise la trajectoire.

Si un objet a une surface courbe, elle peut être localement approchée par un cercle. Ainsi, si l'on connaît les propriétés du cercle, on connaît les propriétés locales de l'objet. C'est ce qui a donné les notions de cercle osculateur, de rayon de courbure et d'harmonique sphérique.

Si l'on dispose des objets ou des personnes en cercle, on sait que l'on peut les atteindre avec le même effort depuis le centre, mais aussi que l'on peut les voir de la même manière, ce qui peut faciliter la surveillance. On peut aussi les désigner en faisant appel à un seul paramètre, la direction ; c'est par exemple l'intérêt des cadrans à aiguille. Cela donne aussi les notions de coordonnées cylindriques et sphériques.

De par sa définition, le cercle euclidien est très simple à tracer : il suffit d'avoir un objet dont les deux extrémités ont une distance constante, une corde tendue par exemple ou une branche (même tordue), ou de manière plus courante un compas. Il est donc simple de tracer un cercle « parfait », ce qui en fait un outil d'étude privilégié pour la géométrie.

Pour des problèmes et des formes plus complexes, on peut faire appel à la notion d'ellipse.

Le cercle peut servir à représenter de manière symbolique des objets « plus ou moins ronds » :

• des astres (planètes, lunes, étoiles) et leurs orbites (qui sont en fait elliptiques) ;
• l’ovale d'un visage (la tête à Toto, les smileys) ;
• un orifice.

Du point de vue purement symbolique, il représente :

• une certaine forme de perfection, de par sa symétrie et son absence d'aspérité, car, selon Ronsard, « rien n'est excellent au monde s'il n'est rond »^[2] ; depuis l'Antiquité grecque, la sphéricité est associée à la perfection, et par conséquent à la divinité^[3] ; pour Kepler, le cercle représente la sainte Trinité, « Le Père au centre, le Fils à la superficie, le Saint Esprit dans l'égalité de la relation du centre au pourtour. Et bien que le centre, la surface et l'intervalle soient manifestement trois, pourtant ils ne font qu'un, au point qu'on ne peut même pas concevoir qu'il en manque un sans que le tout soit détruit^[3],[4] » ;
• un mouvement continu et infini, la notion de cycle ; il est une des représentations du recommencement (ouroboros), de la continuité, de l'éternité et du temps cyclique (voir la roue du temps du Tantra de kalachakra), avec la variante de la spirale ;
• une égalité entre les personnes, comme pour la Table ronde du roi Arthur.

Définitions

Divers objets géométriques liés au cercle.

Pendant longtemps, le langage courant a employé le mot « cercle » autant pour nommer la courbe (circonférence) que la surface qu'elle délimite^[5]. De nos jours, en mathématiques, le cercle désigne exclusivement la ligne courbe, la surface étant, quant à elle, appelée disque.

Le rapport de la circonférence d'un cercle à son diamètre définit le nombre π (Pi).

D'autres termes méritent d’être définis :

• une corde est un segment de droite dont les extrémités se trouvent sur le cercle ;
• un arc est une portion de cercle délimitée par deux points ;
• une flèche est le segment reliant les milieux d'un arc de cercle et d'une corde définis par deux mêmes points du cercle ;
• un rayon est un segment de droite joignant le centre à un point du cercle ;
• un diamètre est une corde passant par le centre ; c'est un segment de droite qui délimite le disque en deux parts égales. Le diamètre est composé de deux rayons colinéaires ; sa longueur est 2r où r est le rayon du cercle ;
• un disque est une région du plan délimitée par un cercle ;
• un secteur circulaire est une partie du disque comprise entre deux rayons ;
• un segment circulaire est une portion de disque comprise entre une corde et l'arc de cercle qu'elle sous-tend ;
• un angle au centre est un angle formé par deux rayons du cercle ;
• la circonférence est le périmètre du cercle et est égale à 2πr, où r est le rayon du cercle.

Équations

Équations cartésiennes et paramétriques

Cercle unité : centré sur l'origine du repère et de rayon 1 ; définition du sinus et du cosinus.

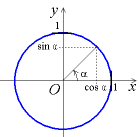
Dans un plan muni d'un repère orthonormé, l’équation cartésienne du cercle de centre C (a,b) et de rayon r est :

${\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}\,}$, soit pour le cercle unité ou cercle trigonométrique (le cercle dont le centre est l'origine du repère et dont le rayon vaut 1) :

${\displaystyle x^{2}+y^{2}=1.}$

Cette équation est en fait une application du théorème de Pythagore pour le triangle rectangle formé par le point du cercle et sa projection sur les deux rayons parallèles aux axes.

En mettant y en évidence, on obtient la double équation cartésienne du cercle (en fait une équation pour chaque demi-cercle délimité par le diamètre horizontal) :

${\displaystyle y=b\pm {\sqrt {r^{2}-(x-a)^{2}}}\,}$.

Des équations paramétriques possibles du cercle (en fonction du paramètre θ qui exprime ici un angle orienté du vecteur joignant le centre du cercle à un de ses points par rapport au vecteur horizontal unité du repère) sont données par :

${\displaystyle x=a+r\cos \theta$ ;\qquad y=b+r\sin \theta }

soit, pour un cercle centré sur l'origine (0 ; 0) :

${\displaystyle x=r\cos \theta$ ;\qquad y=r\sin \theta }

et pour le cercle unité :

${\displaystyle x=\cos \theta$ ;\qquad y=\sin \theta } .

Grâce au théorème de l'angle inscrit dans un demi-cercle et à sa réciproque, on peut également déterminer une équation pour le cercle C de diamètre [AB] :

${\displaystyle {\begin{aligned}M\in C&\Leftrightarrow {\overrightarrow {MA}}\perp {\overrightarrow {MB}}\\&\Leftrightarrow {\overrightarrow {MA}}\cdot {\overrightarrow {MB}}=0\\&\Leftrightarrow {\binom {x-x_{A}}{y-y_{A}}}\cdot {\binom {x-x_{B}}{y-y_{B}}}=0\\&\Leftrightarrow \left(x-x_{A}\right)\left(x-x_{B}\right)+\left(y-y_{A}\right)\left(y-y_{B}\right)=0\\&\Leftrightarrow x^{2}+y^{2}-\left(x_{A}+x_{B}\right)x-\left(y_{A}+y_{B}\right)y+x_{A}x_{B}+y_{A}y_{B}=0.\end{aligned}}}$

Points d'intersection avec une droite

La géométrie analytique permet de déterminer l'intersection d'un cercle et d'une droite. Sans perte de généralité, l'origine du repère est le centre du cercle et l'axe des abscisses est parallèle à la droite. Il s'agit alors de résoudre un système de la forme :

${\displaystyle x^{2}+y^{2}=r^{2}\quad {\rm {et}}\quad y=y_{0}}$,

donc de chercher les solutions x de

${\displaystyle x^{2}=r^{2}-y_{0}^{2}}$.

Trois cas se présentent, selon que la distance entre le centre du cercle et la droite est plus grande que le rayon, égale, ou plus petite :

• si ${\displaystyle |y_{0}|>r}$, l'intersection est vide ;
• si ${\displaystyle |y_{0}|=r}$, la droite est tangente au cercle au point ${\displaystyle (0,y_{0})}$ ;
• si ${\displaystyle |y_{0}|<r}$, il existe deux points d'intersection : ${\displaystyle (+{\sqrt {r^{2}-y_{0}^{2}}},y_{0}){\text{ et }}(-{\sqrt {r^{2}-y_{0}^{2}}},y_{0})}$.

Le cercle vu comme section

Un cercle est une section droite d'un cône de révolution.

Représentation conventionnelle d'un cercle en dessin industriel.

Le cercle est une ellipse dont les foyers sont confondus au centre du cercle ; la longueur du grand axe est égale à la longueur du petit axe. C'est une conique dont l'excentricité e vaut 0. Elle peut être obtenue par l'intersection d'un plan avec un cône de révolution lorsque le plan est perpendiculaire à l'axe de révolution du cône (on parle parfois de « section droite » du cône).

En dessin industriel, un cercle est le plus souvent représenté avec son axe horizontal et son axe vertical (en traits d'axe : trait fin composé de tirets longs et courts), ou bien simplement avec son centre matérialisé par une croix droite « + » en traits fins. Une forme de révolution, pleine ou creuse (cylindre, cône, sphère) et vue selon l'axe de révolution est représentée par un cercle.

Propriétés géométriques

Mesures

La longueur d'un arc de rayon r sous-tendu par un angle au centre α, exprimé en radians, est égale à αr. Ainsi, pour un angle de 2π (un tour complet), la longueur du cercle vaut 2πr.

L'aire du disque délimité par un cercle de rayon r vaut πr² ; si l'on prend une corde de longueur l donnée et que l'on s'en sert pour délimiter une surface fermée, la surface ayant la plus grande aire est délimitée par un cercle.

Selon la légende de la fondation de Carthage, le souverain avait permis aux Phéniciens de fonder une ville dont le pourtour serait délimité par une peau de vache ; Didon en fit une grande lanière et choisit une forme circulaire pour avoir la plus grande surface.

Corde et flèche d'un arc

La longueur d'une corde sous-tendue par un angle α est égale à 2r sin(α/2).

On peut exprimer le rayon r d'un cercle, la corde c et la flèche f d'un quelconque de ses arcs, selon deux d'entre eux, en appliquant le théorème de Pythagore au triangle rectangle formé par r – f, c/2 et r qui est l'hypoténuse :

${\displaystyle c=2{\sqrt {(2r-f)f}};\qquad r={\frac {4f^{2}+c^{2}}{8f}};\qquad f=r-{\sqrt {r^{2}-{\tfrac {c^{2}}{4}}}}}$.

La sinuosité de deux arcs de cercle semblables opposés joints dans le même plan en continûment dérivable est indépendante du rayon du cercle.

Tangente

Trouver le point de tangence.

Tangente perpendiculaire au rayon.

La tangente en un point du cercle est la perpendiculaire au rayon en ce point.

Cette propriété a des applications en optique géométrique : un rayon lumineux passant par le centre d'un miroir sphérique repart en sens inverse selon la même direction (on a une réflexion perpendiculaire au miroir). Si l'on met une ampoule au centre d'un miroir sphérique, la lumière est renvoyée de l'autre côté, ce qui permet par exemple, de « rabattre » la lumière vers un miroir parabolique (principe du contre-miroir).

Considérons un cercle de centre O et un point A extérieur à ce cercle. On cherche une tangente à ce cercle passant par A ; le point de tangence est appelé T.

On utilise le fait que le triangle AOT est rectangle en T. Ce triangle rectangle est donc inscrit dans un cercle dont le centre est le milieu de [AO], ou encore, ce qui est équivalent, que l'hypoténuse a une longueur double de la médiane issue de l'angle droit.

On détermine donc le milieu I de [AO], puis on trace un arc de cercle de centre I et de rayon IO. Cet arc de cercle coupe le cercle aux points de tangence.

Médiatrice

La médiatrice d'une corde passe par le centre.

La médiatrice d'une corde passe par le centre du cercle. Ceci permet de trouver le centre d'un cercle : il suffit de tracer deux cordes non parallèles et de rechercher l'intersection de leurs médiatrices.

On peut aussi montrer que les trois médiatrices d'un triangle sont concourantes et que le point de concours est le centre du cercle passant par les trois sommets, appelé cercle circonscrit au triangle.

Cercle et triangle rectangle

Triangle rectangle inscrit dans un cercle.

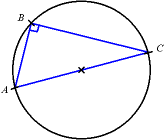
Prenons sur un cercle trois points A, B et C, dont deux — A et C — sont diamétralement opposés (c'est-à-dire que [AC] est un diamètre). Alors, le triangle ABC est rectangle en B.

Ceci découle du fait que la médiane issue de l'angle droit vaut la moitié de l'hypoténuse (on a un rayon et un diamètre) ; ceci est une propriété du triangle appelée le théorème de l'angle inscrit dans un demi-cercle, ou théorème de Thalès (en Allemagne et certains pays anglophones).

Réciproquement, soit A et C deux points diamétralement opposés d'un cercle. Soit B un point du plan tel que ABC soit rectangle en B. Alors B appartient au cercle^[6].

Angle inscrit, angle au centre

Illustration de la relation entre les secteurs angulaires interceptant un même arc.

Prenons deux points distincts A et B du cercle. O est le centre du cercle et C est un autre point du cercle. Alors, on a

${\displaystyle {\widehat {AOB}}=2\times {\widehat {ACB}}}$

Pour l'angle au centre ${\displaystyle {\widehat {AOB}}}$, il faut considérer le secteur angulaire qui intercepte l'arc opposé à l'arc contenant C.

Cette propriété est utilisée dans les appareils d'analyse spectrale par dispersion de longueur d'onde, c'est la notion de cercle de focalisation ou cercle de Rowland.

Puissance d'un point par rapport à un cercle

Puissance d'un point par rapport à un cercle.

Si M est un point et Γ est un cercle de centre O et de rayon R, alors, pour toute droite passant par M et rencontrant le cercle en A et B, on a

${\displaystyle MA\times MB=|OM^{2}-R^{2}|}$.

Cette valeur ne dépend pas de la droite choisie, mais seulement de la position de M par rapport au cercle.

On peut remarquer que

• si M est à l’extérieur du cercle,${\displaystyle MA\times MB=OM^{2}-R^{2}}$ ;
• si M est à l’intérieur du cercle, ${\displaystyle OM^{2}-R^{2}=-MA\times MB}$ ;ce produit correspond au produit des mesures algébriques MA et MB.

On appelle alors puissance du point M par rapport au cercle Γ le produit des mesures algébriques MA et MB. Ce produit est indépendant de la droite choisie et vaut toujours ${\displaystyle OM^{2}-R^{2}}$.

Lorsque le point M est à l'extérieur du cercle, il est possible de mener des tangentes au cercle. En appelant T le point de contact d'une de ces tangentes, d'après le théorème de Pythagore dans le triangle OMT, la puissance de M est MT².

L'égalité :

${\displaystyle MA\times MB=MT^{2}}$

est suffisante pour affirmer que la droite (MT) est tangente au cercle.

La puissance d'un point permet de vérifier que quatre points sont cocycliques : en effet, si

• A, B, C, D sont quatre points tels que (AB) et (CD) se coupent en M et
• MA×MB = MC×MD (en mesures algébriques),

alors les quatre points sont cocycliques.

Rapport des cercles inscrits

Illustration de l'unique disposition de N cercles inscrits, pour N de 2 à 7.

• Rayon ${\displaystyle R'}$ et surface ${\displaystyle S'}$ des 2 plus grands cercles inscrits dans le cercle de rayon R et de surface S :

  ${\displaystyle R'={\frac {R}{2}}\,;\qquad 2\,S'={\frac {S}{2}}}$

• Rayon ${\displaystyle R'}$ et surface ${\displaystyle S'}$ des 3 plus grands cercles inscrits :

  ${\displaystyle R'={\frac {R}{1+{\sqrt {\frac {4}{3}}}}}\,;\qquad 3\,S'={\frac {9\,S}{7+2{\sqrt {3}}}}}$

• Rayon ${\displaystyle R'}$ et surface ${\displaystyle S'}$ des 4 plus grands cercles inscrits :

  ${\displaystyle R'={\frac {R}{1+{\sqrt {2}}}}=({\sqrt {2}}-1)\,R\,;\qquad 4\,S'={\frac {4\,S}{3+{\sqrt {8}}}}}$

• Rayon ${\displaystyle R'}$ des 5 plus grands cercles inscrits :

  ${\displaystyle R'={\frac {R}{1+{\sqrt {2+{\sqrt {\frac {4}{5}}}}}}}}$

• Rayon ${\displaystyle R'}$ et surface ${\displaystyle S'}$ des 7 (ou 6) plus grands cercles inscrits (1 cercle au centre entouré de 6) :

  ${\displaystyle R'={\frac {R}{3}}\,;\qquad 7\,S'={\frac {7\,S}{9}}}$.

Inscription de cercles, de même rayon, dans un cercle, un triangle équilatéral, un carré^[7]

Notes et références

1. Voir la définition de l'adjectif rond sur le site du CNRTL.
2. Pierre de Ronsard, Réponse aux injures et calomnies de je ne sais quels prédicants et ministres de Genève, 1563.
3. « Les avancées grecques : Le cercle et la sphère », sur Les galeries virtuelles de la Bibliothèque nationale de France.
4. Johannes Kepler, Le Mystère cosmographique, 1596.
5. Dans l'encyclopédie de Diderot et d'Alembert, par exemple, le cercle est «l'espace renfermé par la circonférence» (s:L’Encyclopédie/1re édition/CERCLE) et le dictionnaire Robert édition 1993, donne, comme troisième sens au mot cercle : « par extension courante : surface plane limitée par un cercle ».
6. Jean Dieudonné, Algèbre linéaire et géométrie élémentaire, Paris, Hermann, 1964, ex.2p.96
7. Retrouver ces figures d'inscription de cercles dans la page empilements dans le plan.

Voir aussi

Sur les autres projets Wikimedia :

• Cercle, sur Wikimedia Commons
• cercle, sur le Wiktionnaire
• Cercle, sur Wikisource

• Cercle généralisé (en)
• Livre III des Éléments d'Euclide
• Disque — Sphère — Boule

• Portail de la géométrie