Rayon (géométrie)

Pour les articles homonymes, voir Rayon.

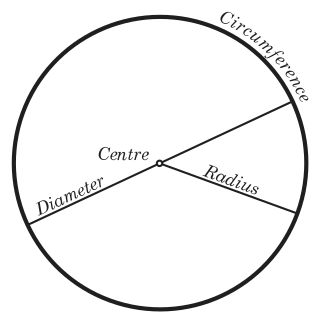
En géométrie, un rayon d'un cercle ou d'une sphère est un segment de droite quelconque reliant son centre à sa circonférence. Par extension, le rayon d'un cercle ou d'une sphère est la longueur de chacun de ces segments. Le rayon est la moitié du diamètre. En sciences et en ingénierie, le terme rayon de courbure est souvent utilisé comme synonyme de rayon.

Plus généralement — en géométrie, ingénierie, théorie des graphes et dans nombre d'autres contextes — le rayon d'un objet (par exemple un cylindre, un polygone, un graphe ou une pièce mécanique) est la distance de son centre ou axe de symétrie à ses points de surface les plus éloignés. Dans ce cas, le rayon peut être différent de la moitié du diamètre (dans le sens de plus grande distance entre deux points de l'objet)^[1].

Il peut aussi avoir plusieurs définitions spécifiques comme on le verra pour l'ellipse ci-dessous.

Rayon d'un cercle

La relation entre le rayon $R$ et la circonférence $L$ d'un cercle est $R={\frac {L}{2\pi }}$ .

Pour calculer le rayon $R$ d'un cercle passant par trois points $A,B,C$ on peut utiliser la formule suivante (voir Théorème de l'angle inscrit, Angle inscrit dans un demi-cercle et la figure ci-contre) : $R={\frac {a}{2\sin \alpha }}$ , où $a$ est la longueur $BC$ et $\alpha$ la mesure de l'angle ${\widehat {BAC}}$ .

Si les trois points sont donnés par leurs coordonnées $(x_{1},y_{1})$ , $(x_{2},y_{2})$ et $(x_{3},y_{3})$ , on peut aussi utiliser la formule suivante (voir Loi des sinus et Aire d'un triangle) :

$R={\frac {\sqrt {\left(\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}\right)\left(\left(x_{2}-x_{3}\right)^{2}+\left(y_{2}-y_{3}\right)^{2}\right)\left(\left(x_{3}-x_{1}\right)^{2}+\left(y_{3}-y_{1}\right)^{2}\right)}}{2\left|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3}-x_{2}y_{1}-x_{3}y_{2}\right|}}$ .

Rayons d'une ellipse

Résumé

Contexte

Article connexe : Ellipse (mathématiques).

Articles détaillés : Grand axe, Petit axe et Excentricité (mathématiques).

On peut définir plusieurs notions de rayon pour une ellipse, notions redonnant celle de rayon classique dans le cas du cercle.

Le demi grand axe $a$ de l'ellipse s'interprète comme le rayon du cercle circonscrit à l'ellipse, ou cercle principal , et le demi petit axe comme le rayon du cercle inscrit, ou cercle secondaire. On peut définir comme "rayon moyen", la moyenne arithmétique de ces deux rayons : $R_{1}=(a+b)/2$ .

Le rayon surfacique est le rayon d'un cercle d'aire (surface) égale à celle de l'ellipse.

Il est égal à la racine carrée du produit des deux demi-axes de l'ellipse :

R_{2}={\sqrt {ab}}=a{\sqrt[{4}]{1-e^{2}}}

où

e

est l'excentricité de l'ellipse

C'est donc la moyenne géométrique des demi-axes.

Un autre rayon remarquable de l'ellipse est la distance moyenne d'un point parcourant l'ellipse à vitesse constante au foyer de cette ellipse. Ce rayon, qui est par définition égal à $R_{3}={{\int _{0}^{2\pi }{{\sqrt {(a(\cos t-e)^{2}+b^{2}\sin ^{2}t}}\,{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,\mathrm {d} t}} \over {\int _{0}^{2\pi }{{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,\mathrm {d} t}}}$ se simplifie en la valeur $R_{3}=a$ du demi grand axe.

La distance moyenne à vitesse constante au centre de l'ellipse : $R_{4}={{\int _{0}^{2\pi }{{\sqrt {a^{2}\cos ^{2}t+b^{2}\sin ^{2}t}}\,{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,\mathrm {d} t}} \over {\int _{0}^{2\pi }{{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,\mathrm {d} t}}}$ ne donne pas, elle, une valeur simple.

La distance moyenne au centre de l'ellipse, à vitesse de l'anomalie excentrique t constante : $R_{5}={1 \over {2\pi }}{\int _{0}^{2\pi }{{\sqrt {a^{2}\cos ^{2}t+b^{2}\sin ^{2}t}}\,\mathrm {d} t}}$ est égale, elle, à $L \over {2\pi }$ où $L$ est la longueur de l'ellipse. C'est donc le rayon d'un cercle de longueur égale à celle de l'ellipse.
On peut aussi considérer l'écart-type de la distance entre deux points de l'intérieur de l'ellipse : ${\sqrt {\frac {\iint (M_{1}M_{2})^{2}dM_{1}dM_{2}}{\iint dM_{1}dM_{2}}}}$ , soit ${\sqrt {\frac {\int _{0}^{1}\int _{0}^{1}\int _{0}^{2\pi }\int _{0}^{2\pi }((ar_{1}\cos t_{1}-br_{2}\cos t_{2})^{2}+(ar_{1}\cos t_{1}-br_{2}\cos t_{2})^{2})r_{1}r_{2}dr_{1}dr_{2}dt_{1}dt_{2}}{\int _{0}^{1}\int _{0}^{1}\int _{0}^{2\pi }\int _{0}^{2\pi }r_{1}r_{2}dr_{1}dr_{2}dt_{1}dt_{2}}}}$ qui se simplifie en $R_{6}={\sqrt {\frac {a^{2}+b^{2}}{2}}}$ , moyenne quadratique des demi-axes.

Rayons d'un ellipsoïde

Résumé

Contexte

Rayon moyen

Le "rayon moyen" est égal à la moyenne arithmétique des 3 demi-axes :

R_{1}={\frac {a+b+c}{3}}

Rayon volumétrique

Le rayon volumétrique est le rayon d'une sphère fictive de volume égal à celui de l'ellipsoïde considéré.

Il est égal à la moyenne géométrique des demi-axes :

R_{2}={\sqrt[{3}]{abc}}

Rayon authalique

Le rayon authalique est le rayon d'une sphère fictive d'aire (surface) égale à l'aire $S$ de l'ellipsoïde considéré, donc $R_{3}={\sqrt {S/4\pi }}$ .

Par exemple dans le cas d'un ellipsoïde de révolution allongé (rotation d'une ellipse autour de son grand axe) $R_{3}={\sqrt {{\frac {b^{2}}{2}}+{\frac {ab}{2}}{\frac {\arcsin e}{e}}}}$ .

Rayon d'un polygone

Résumé

Contexte

Un rayon d'un polygone régulier est un segment reliant le centre de ce polygone à l'un de ses sommets. Sa longueur est par conséquent le rayon du cercle circonscrit à ce polygone.

Le rayon d'un polygone à $n$ côtés de longueur $c$ est donc égal à

${\sqrt {\frac {c^{2}}{2-2\cos(2\pi /n)}}}={\frac {c}{2\sin(\pi /n)}}$

ou encore, en fonction de la longueur de l'apothème $h$ , à

${\frac {h}{\cos(\pi /n)}}$ .

Rayons de la Terre

Résumé

Contexte

Données

Davantage d’informations Valeur en kilomètres, Commentaire ...

Rayon	Valeur en kilomètres	Commentaire
maximal	6 384,4	au sommet du Chimborazo
minimal	6 352,8
équatorial	6 378,8	demi-grand axe de l'ellipsoïde de référence
polaire	6 356,8	demi-petit axe de l'ellipsoïde de référence
moyen	6 371,009
authalique	6 371,007 2
volumétrique	6 371,000 8

Fermer

Historique

La première mesure du rayon de la Terre en astronomie a été effectuée par Ératosthène. Son calcul est le suivant : le Soleil est si éloigné que ses rayons arrivent parallèlement en tout point de la Terre. Il a lu qu'à Syène, les rayons tombent verticalement dans un puits le jour du solstice d'été. Cela veut dire que le Soleil passe par le zénith, il n'y a alors pas d'ombre. Plus au nord, au même instant, les rayons atteignent Alexandrie sous un angle non nul, qu'il mesure. L'angle mesuré est de un cinquantième de cercle. Cela signifie que la circonférence de la Terre est cinquante fois plus grande que la distance Syène-Alexandrie. Il avait lu également que les caravanes de chameaux partant de Syène mettaient cinquante jours pour arriver à Alexandrie en parcourant cent stades par jour. Il calcula que la distance entre les deux villes de la vallée du Nil était de 5 000 stades. Le stade équivaut à 158 m.

Par la mesure de l'ombre portée par ces objets de hauteur connue situés en deux points de latitude différente, il trouve la valeur de 250 000 stades pour la longueur du méridien, c'est-à-dire la circonférence terrestre. Cette mesure est exacte à 2 % près. Il en déduisit le rayon terrestre.

Utilisation

Le rayon terrestre est utilisé pour de nombreux calculs astronomiques comme le calcul de la parallaxe diurne d'un astre :

Parallaxe diurne : deux observateurs se placent en deux points A et B de la Terre les plus éloignés possible et notent la configuration des étoiles entourant l'astre observé. Ils peuvent ainsi calculer les angles

{\widehat {ABP}}

{\widehat {BAP}}

, puis en déduire la parallaxe qui permettra d'obtenir la distance TP.

Notes et références

[1]
Par exemple, un tronc de cylindre de révolution de hauteur h et de rayon r a un diamètre égal à h si h > 2r, et dans ce cas $r\neq h/2$ .

Voir aussi

Bibliographie

Michel Morin et Alain Roy, Géométrie 4 : les relations dans le cercle, Mont-Royal (Québec), Modulo, 1995 (OCLC 32548158)

Portail de la géométrie

Wikiwand in your browser!

Seamless Wikipedia browsing. On steroids.

Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.

Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.

Wikiwand for Chrome

Wikiwand for Edge

Wikiwand for Firefox

Rayon d'un cercle

La relation entre le rayon $R$ et la circonférence $L$ d'un cercle est $R={\frac {L}{2\pi }}$ .

Si les trois points sont donnés par leurs coordonnées $(x_{1},y_{1})$ , $(x_{2},y_{2})$ et $(x_{3},y_{3})$ , on peut aussi utiliser la formule suivante (voir Loi des sinus et Aire d'un triangle) :

Rayons d'une ellipse

Résumé

Contexte

Article connexe : Ellipse (mathématiques).

Articles détaillés : Grand axe, Petit axe et Excentricité (mathématiques).

On peut définir plusieurs notions de rayon pour une ellipse, notions redonnant celle de rayon classique dans le cas du cercle.

Le demi grand axe $a$ de l'ellipse s'interprète comme le rayon du cercle circonscrit à l'ellipse, ou cercle principal , et le demi petit axe comme le rayon du cercle inscrit, ou cercle secondaire. On peut définir comme "rayon moyen", la moyenne arithmétique de ces deux rayons : $R_{1}=(a+b)/2$ .

Le rayon surfacique est le rayon d'un cercle d'aire (surface) égale à celle de l'ellipse.

Il est égal à la racine carrée du produit des deux demi-axes de l'ellipse :

R_{2}={\sqrt {ab}}=a{\sqrt[{4}]{1-e^{2}}}

où

e

est l'excentricité de l'ellipse

C'est donc la moyenne géométrique des demi-axes.

Un autre rayon remarquable de l'ellipse est la distance moyenne d'un point parcourant l'ellipse à vitesse constante au foyer de cette ellipse. Ce rayon, qui est par définition égal à $R_{3}={{\int _{0}^{2\pi }{{\sqrt {(a(\cos t-e)^{2}+b^{2}\sin ^{2}t}}\,{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,\mathrm {d} t}} \over {\int _{0}^{2\pi }{{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,\mathrm {d} t}}}$ se simplifie en la valeur $R_{3}=a$ du demi grand axe.

La distance moyenne à vitesse constante au centre de l'ellipse : $R_{4}={{\int _{0}^{2\pi }{{\sqrt {a^{2}\cos ^{2}t+b^{2}\sin ^{2}t}}\,{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,\mathrm {d} t}} \over {\int _{0}^{2\pi }{{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,\mathrm {d} t}}}$ ne donne pas, elle, une valeur simple.

La distance moyenne au centre de l'ellipse, à vitesse de l'anomalie excentrique t constante : $R_{5}={1 \over {2\pi }}{\int _{0}^{2\pi }{{\sqrt {a^{2}\cos ^{2}t+b^{2}\sin ^{2}t}}\,\mathrm {d} t}}$ est égale, elle, à $L \over {2\pi }$ où $L$ est la longueur de l'ellipse. C'est donc le rayon d'un cercle de longueur égale à celle de l'ellipse.
On peut aussi considérer l'écart-type de la distance entre deux points de l'intérieur de l'ellipse : ${\sqrt {\frac {\iint (M_{1}M_{2})^{2}dM_{1}dM_{2}}{\iint dM_{1}dM_{2}}}}$ , soit ${\sqrt {\frac {\int _{0}^{1}\int _{0}^{1}\int _{0}^{2\pi }\int _{0}^{2\pi }((ar_{1}\cos t_{1}-br_{2}\cos t_{2})^{2}+(ar_{1}\cos t_{1}-br_{2}\cos t_{2})^{2})r_{1}r_{2}dr_{1}dr_{2}dt_{1}dt_{2}}{\int _{0}^{1}\int _{0}^{1}\int _{0}^{2\pi }\int _{0}^{2\pi }r_{1}r_{2}dr_{1}dr_{2}dt_{1}dt_{2}}}}$ qui se simplifie en $R_{6}={\sqrt {\frac {a^{2}+b^{2}}{2}}}$ , moyenne quadratique des demi-axes.

Rayons d'un ellipsoïde

Résumé

Contexte