在幾何學 中,菱形十二面體 (Rhombic dodecahedron )是一個由菱形 構成的十二面體 [ 2] 全等 的菱形 組成,具有24條邊 和14個頂點 ,其對偶多面體 為截半立方體 [ 3] 卡塔蘭立體 之一。
其具有面可遞 的性質,這意味著這個幾何形狀 的對稱性 可在各個面 上遞移。菱形十二面體是一種可以獨立堆砌 並無空隙且不重疊地填滿三維空間 的立體,因此是一種空間填充多面體 [ 4] 堆砌 結構可以對應到化學 中的體心立方晶格 ;此外,在礦物學 中,菱形十二面體也是部分礦物的晶體慣態 [ 5] 骰子 或被設計成魔術方塊 。菱形十二面體有數種拓樸同構體,即幾何上不同,但面的數量與每個面的邊數相同、頂點間連接方式也相同的立體,例如鳶形十二面體 。菱形十二面體也可以星形化 星形菱形十二面體 ,當中較知名的形狀是艾雪立體 。
菱形十二面體能獨立密鋪三維空間 菱形十二面體旋轉透視圖
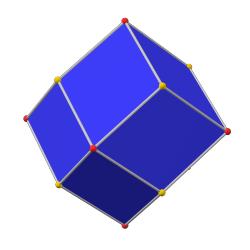
菱形十二面體是一個卡塔蘭立體 ,有12個面 、24條邊和14個頂點 [ 1] :3 ,其中12面為12個全等 的個菱形 ,且具有180度旋轉對稱性和點對稱性,因此是一個環帶多面體 [ 6] 對偶多面體 為截半立方體 。
菱形十二面體能獨立密鋪三維空間,因此是一種空間填充多面體 [ 4] 菱形十二面體堆砌 ,可以視為是面心立方晶格的沃罗诺伊鑲嵌 。這種堆砌體 是體心立方晶格 (bcc)的布里元區 ,部分礦物可以形成於菱形十二面體的晶體慣態 [ 5] 石榴石 。蜜蜂築巢時也是使用菱形十二面體空間填充的幾何結構來築巢,其每個蜂房皆是以半個菱形十二面體為上蓋之六角柱的空間填充構成[ 7] [ 8] 鑽石 和金剛石 的單位晶格中,但實際上少了4個頂點,而化學鍵 位於剩餘的稜上[ 9]
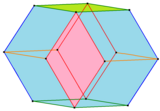
菱形十二面體可以從中心分割成4個三方偏方面體 ,若將菱形十二面體空間填充的每一個菱形十二面體都分割成三方偏方面體則可以形成三方偏方面體的空間填充[ 10] [ 11] 正六邊形鑲嵌 的六邊形 切割成3個菱形而形成菱形鑲嵌 。
菱形十二面體
菱形十二面體的分割
正六邊形的分割
菱形十二面體可以透過將一個立方體切割成6個四角錐重新組合而成
[ 12] 。
菱形十二面體的對偶多面體 ——截半立方體 是一個阿基米德立體 ,具有點可遞 的性質,因此菱形十二面體具有面可遞的性質,這意味著這個幾何形狀的對稱群可在各個面上傳遞,換句話說,這立體上的任意兩個面A和B,若透過旋轉或鏡射這個立體,使A移動到B原來的位置時,而兩個面仍然佔據了相同的空間區域[ 13]
同理,菱形十二面體具有邊可遞的特性,這意味著,這立體上的任意兩條稜A和B,透過旋轉或鏡射這個立體,使A移動到B原來的位置時,其稜以及其二面角仍然佔據了相同的空間區域[ 14] [ 15] [ 16]
菱形十二面體由12個全等的菱形組成,這個菱形的長對角線都是短對角線 的√2 鋭角 的角度則為arccos (1 / 3 鈍角 的角度則為 109.47°[ 17] [ 1] :5 ,兩條對角線長度與一邊長的比為
2
:
1
:
3
/
2
{\displaystyle {\sqrt {2}}:1:{\sqrt {3}}/2}
[ 18]
若菱形十二面體的邊長為a 內切球 半徑為:[ 19] [ 註 2]
r
i
=
6
3
a
≈
0.816
496
5809
a
{\displaystyle r_{\mathrm {i} }={\frac {\sqrt {6}}{3}}a\approx 0.816\,496\,5809a\,}
OEIS 數列A157697 )邊心距 為:[ 19] [ 註 4]
r
m
=
2
2
3
a
≈
0.942
809
041
58
a
{\displaystyle r_{\mathrm {m} }={\frac {2{\sqrt {2}}}{3}}a\approx 0.942\,809\,041\,58a\,}
OEIS 數列A179587 )外接球 半徑為:
r
o
=
2
3
3
a
≈
1.154
700
538
a
{\displaystyle r_{\mathrm {o} }={\frac {2{\sqrt {3}}}{3}}a\approx 1.154\,700\,538a\,}
OEIS 數列A020832 )
若菱形十二面體的邊長為a 表面積 A 體積 V [ 19] [ 註 6]
A
=
8
2
a
2
≈
11.313
7085
a
2
V
=
16
3
9
a
3
≈
3.079
201
44
a
3
{\displaystyle {\begin{aligned}A&=8{\sqrt {2}}a^{2}\approx 11.313\,7085a^{2}\\V&={\frac {16{\sqrt {3}}}{9}}a^{3}\approx 3.079\,201\,44a^{3}\end{aligned}}}
若令其對偶多面體——截半立方體邊長為單位長,則菱形十二面體的邊長為
3
6
8
{\displaystyle {\frac {3{\sqrt {6}}}{8}}}
V 為[ 19]
V
=
27
2
16
≈
2.386
485
386
5
{\displaystyle V={\frac {27{\sqrt {2}}}{16}}\approx 2.386\,485\,386\,5}
[ 19]
五角十二面體 (Pyritohedron[ 20] 擴展
三個菱形之公共頂點(共8個)其頂點坐標 為[ 4]
(±1, ±1, ±1) 另外6個頂點為四個菱形之公共頂點,其頂點坐標為[ 4]
(±2, 0, 0), (0, ±2, 0) 和 (0, 0, ±2) 菱形十二面體可以是為五角十二面體的退化限制,其頂點坐標可表示為(±1, ±1, ±1) 與(0, 1 + h , 1 − h 2 ) ,其中h = 1。
菱形十二面體有4個特殊的正交投影,分別為於四個菱形的公共頂點投影、於三個菱形的公共頂點投影、於稜上投影和於面上投影,其中「於稜上投影」以及「於面上投影」其對稱性對應於B2 和 A2 的考克斯特平面[ 21]
亦有一些十二面體也是由菱形組成,例如比林斯基十二面體 [ 22]
菱形十二面體是一種平行多面體 ,具有可以獨立填滿三維空間的性質,其所形成的幾何結構稱為菱形十二面體堆砌 或平行十二面體堆砌[ 23]
常見的由菱形組成的平行十二面體有二面體群菱形十二面體 。
二面體群菱形十二面體 是一種具有與一般菱形十二面體不同對稱性的平行十二面體,同樣可以獨立填滿三維空間,其所形成的幾何結構類似於截角八面體堆砌 的一個變種[ 24]
其中一個二面體群菱形十二面體例子,例如由4個正方形和8個60度菱形所組成的平行十二面體,其具有D4h 二面體群 對稱,且階數為16,其外型看起來與頂面和底面擺入正四角錐的截半立方體類似。
頂點座標
(0, 0, ±2)
(±1, ±1, 0)
(±1, 0, ±1)
(0, ±1, ±1)
主条目:比林斯基十二面體
比林斯基十二面體 (Bilinski dodecahedron )又稱為第二種菱形十二面體 (菱形十二面体第2種 [ 25] [ 26] 斯坦科·比林斯基
比林斯基十二面體同樣由12個菱形組成,但構成此幾何體的菱形有兩種:其中一種菱形對角線比為2個平方根,另一種菱形對角線比為黃金比例 [ 27] [ 28]
更多信息 第一種, 第二種 ...
面的種類
第一種
第二種
√2 :1
√5 + 1/ 2
关闭
菱形十二面體形狀的骰子 。 由於菱形十二面體每個面全等,且十分均勻,因此有時會被拿來做成骰子 (但大多数都会使用正十二面体 作为骰子)。亦有部分的魔術方塊 是設計成菱形十二面體的形狀[ 29]
菱形十二面體可以經由立方體透過會合變換構造,即將立方體每個面貼上角錐,並用適當的錐高,使角錐側面與鄰近面上貼的角錐之測面共面來獲得。其他也是由立方體透過康威變換得到的多面體有:
更多信息 对称性: [4,3], (*432), [4,3]+, (432) ...
半正正八面体家族多面体
对称性 : [4,3] , (*432)
[4,3]+ , (432)
[1+ ,4,3], (*332)
[4,3+ ], (3*2)
{4,3}
t0,1 {4,3}
t1 {4,3}
t1,2 {4,3}
{3,4}
t0,2 {4,3}
t0,1,2 {4,3}
s{4,3}
h{4,3}
h1,2 {4,3}
半正多面体的对偶
V4.4.4
V3.8.8
V3.4.3.4
V4.6.6
V3.3.3.3
V3.4.4.4
V4.6.8
V3.3.3.3.4
V3.3.3
V3.3.3.3.3
关闭
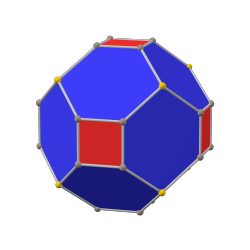
菱形十二面體可以切割成截半立方體 。在切割過程可以得到一些不同的多面體,例如:
更多信息 (可能的來源), 倒角立方體 (截邊立方體) ...
关闭
菱形十二面體與小斜方截半四面體(等價於截半立方體 )的對偶多面體等價,其他與正四面體相關的多面體為:
更多信息 对称性: [3,3], (*332), [3,3]+, (332) ...
正四面体家族半正多面体
对称性 : [3,3] , (*332)
[3,3]+ , (332)
{3,3}
t0,1 {3,3}
t1 {3,3}
t1,2 {3,3}
t2 {3,3}
t0,2 {3,3}
t0,1,2 {3,3}
s{3,3}
半正多面体对偶
V3.3.3
V3.6.6
V3.3.3.3
V3.6.6
V3.3.3
V3.4.3.4
V4.6.6
V3.3.3.3.3
关闭
菱形十二面體可以視為由菱形組成的球面鑲嵌圖,一般菱形鑲嵌 的菱形銳角頂點是3個菱形的公共頂點,有這種性質的相關多面體與鑲嵌包括:
另一種菱形鑲嵌的菱形銳角頂點是4個菱形的公共頂點,而菱形十二面體也屬於這類鑲嵌。有這種性質的相關多面體與鑲嵌包括:
更多信息 *n42 擬正對偶鑲嵌對稱性 V(4.n)2 的變種:, 對稱性*4n2 [n,4] ...
*n 42 擬正對偶鑲嵌對稱性 V(4.n)2 的變種:
對稱性
球面鑲嵌 歐氏鑲嵌 緊湊鑲嵌
仿緊鑲嵌
非緊鑲嵌
*342
*442
*542
*642
*742
*842
*∞42
鑲嵌圖布局
V4.3.4.3
V4.4.4.4
V4.5.4.5 V4.∞.4.∞
关闭
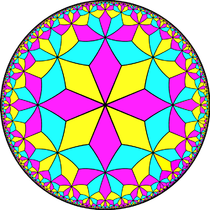
此外,菱形十二面體也可以對應到面布局為V3.2n.3.2n的鑲嵌圖系列中。這個系列的第一種形狀時平面鑲嵌,其餘皆為雙曲鑲嵌:
部分多面體與菱形十二面體拓樸同構,例如平行十二面體 ,亦有一些非菱形組成的十二面體與菱形十二面體拓樸同構,例如鳶形十二面體。
數組(a,b)為(3 / 4 3 / 2 鳶形十二面體 [ 30] [ 31] [ 32] 鳶形 組成的十二面體 ,具有面可遞的性質,並具24階四面體群對稱性。
鳶形十二面體可以視為將菱形十二面體的菱形面變形成鳶形的結果。形變的方式是透過調整菱形十二面體的8個頂點,另外四個頂點保持正四面體的布局位置。其形變量可透過一個數組(a,b)來表示,當a和b皆為1時則為菱形十二面體,a表示保持著正四面體的布局位置的頂點,可以逐漸向1 / 2 1 / 2 扭歪多邊形 ,其值會向正無窮大逼近。這種情形下,其頂點坐標可以表示為:
(±2, 0, 0), (0, ±2, 0), (0, 0, ±2)
(a , a , a ), (−a , −a , a ), (−a , a , −a ), (a , −a , −a )
(−b , −b , −b ), (−b , b , b ), (b , −b , b ), (b , b , −b ) 下表列出部分數組(a,b)所形成的鳶形十二面體圖像:
更多信息 數組(a,b), (1,1) ...
數組(a,b)
(1,1)
(7 / 8 7 / 6
(3 / 4 3 / 2
(2 / 3
(5 / 8 5 / 2
(9 / 16 9 / 2
圖像
关闭
透過將菱形十二面體切割為12個菱形錐可以重新組合成第一種星形菱形十二面體。 如同其他的凸多面體,菱形十二面體也可以透過延伸面或邊,直到它們相遇形成新的多面體來進行星形化。多爾曼·露可(Dorman Luke)在他的論文中描述了一些菱形十二面體的星形化體[ 33]
第一種星形菱形十二面體
第一種星形菱形十二面體的三維模型
對偶複合體是由一個多面體 與其對偶多面體 組合成的複合圖形。菱形十二面體與其對偶的複合體為複合截半立方體菱形十二面體 。其共有26個面、48條邊和26個頂點,其尤拉示性數 為4,虧格 為-1[ 34]
菱形十二面體可以獨立填滿三維空間,其所形成的幾何結構稱為菱形十二面體堆砌 。[ 23]
在圖論 的數學領域中,與菱形十二面體相關的圖為菱形十二面體圖 ,是菱形十二面體之邊與頂點的圖 非哈密顿图 [ 37]
菱形十二面體圖有24條邊和14個頂點 ,其中度 為3的頂點有8個;度 為4的頂點有6個。
菱形十二面體圖的特徵多項式 為[ 37]
(
x
−
2
)
3
x
6
(
x
+
2
)
3
(
x
2
−
12
)
{\displaystyle (x-2)^{3}x^{6}(x+2)^{3}(x^{2}-12)}
色多項式 為[ 37] (x-1) x (x12 -23 x11 +253 x10 -1759 x9 +8615 x8 -31361 x7 +87205 x6 -187127 x5 +308232 x4 -380364 x3 +333138 x2 -184963 x+48831)
此文獻[ 19]
3
6
8
{\displaystyle {\frac {3{\sqrt {6}}}{8}}}
內切球 半徑=
3
4
{\displaystyle {\frac {3}{4}}}
a 內切球 半徑為
3
4
3
6
8
a
=
2
2
3
a
{\displaystyle {\frac {\frac {3}{4}}{\frac {3{\sqrt {6}}}{8}}}a={\frac {2{\sqrt {2}}}{3}}a}
[ 註 1] 此文獻[ 19]
3
6
8
{\displaystyle {\frac {3{\sqrt {6}}}{8}}}
邊心距 =
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
a 邊心距 為
3
2
3
6
8
a
=
2
2
3
a
{\displaystyle {\frac {\frac {\sqrt {3}}{2}}{\frac {3{\sqrt {6}}}{8}}}a={\frac {2{\sqrt {2}}}{3}}a}
[ 註 3] 此文獻[ 19]
3
6
8
{\displaystyle {\frac {3{\sqrt {6}}}{8}}}
體積 =
27
2
16
{\displaystyle {\frac {27{\sqrt {2}}}{16}}}
a 體積 為
27
2
16
(
3
6
8
)
3
a
3
=
16
3
9
a
3
{\displaystyle {\frac {\frac {27{\sqrt {2}}}{16}}{\left({\frac {3{\sqrt {6}}}{8}}\right)^{3}}}a^{3}={\frac {16{\sqrt {3}}}{9}}a^{3}}
[ 註 5]
Cromwell, P. Polyhedra . United Kingdom: Cambridge. 1997: 79 –86 Archimedean solids . ISBN 0-521-55432-2
Stewart, Ian . What Shape is a Snowflake? Magical Numbers in Nature. Weidenfeld & Nicolson. 2001.George W. Hart. Zonohedrification . The Mathematica Journal. 1999, vol. 7 (no. 3) [2018-08-29 ] . (原始内容存档 于2018-11-14). Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things , ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)李政憲、翁條雄、連崇馨. 從立方體切割看菱形12面體與填充空間 . 科學研習. 2017年5月, (No.56-05): 24-32 [2018-08-29 ] . (原始内容存档 于2018-08-29). McLean, K. Robin, Dungeons, dragons, and dice, The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822 .Peter R. Cromwell, Polyhedra , Cambridge University Press 1997, ISBN 0-521-55432-2 , p. 371 Transitivity Coxeter, Harold Scott MacDonald ; Longuet-Higgins, M. S.; Miller, J. C. P., Uniform polyhedra, Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1954, 246 : 401–450, ISSN 0080-4614 JSTOR 91532 MR 0062446 doi:10.1098/rsta.1954.0003 Order in Space: A design source book, Keith Critchlow, p.56–57
P.R. クロムウェル『 多面体』シュプリンガー・フェアラーク東京
H.S.M Coxeter, "Regular polytopes", Dover publications, 1973.
郭君逸. Skewb系列方塊探討 . davidguo.idv.tw. 2018-01-23 [2018-08-29 ] . (原始内容存档 于2016-10-04).
Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X (Section 3-9)Wenninger, Magnus Dual Models . Cambridge University Press. 1983 [2018-08-26 ] . ISBN 978-0-521-54325-5MR 0730208 doi:10.1017/CBO9780511569371 原始内容 存档于2021-04-30).The Symmetries of Things 页面存档备份 ,存于互联网档案馆 ) 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, p. 285, Rhombic dodecahedron )