倒角立方体

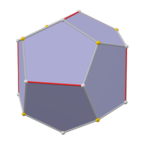
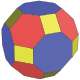
在幾何學中，倒角立方體又稱切稜立方体或裁邊立方體（英語：Chamfered Cube）是一種凸十八面體，共有18個面、48個邊和32個頂點^[1]，是四角化截半立方體的對偶多面體，是由立方體經過倒角變換所產生的多面體，是一種方富勒烯^[3]。

倒角立方體

類別	戈德堡多面體 環帶多面體 擬詹森多面體
對偶多面體	四角化截半立方體
數學表示法
康威表示法	cC hjC t4jC t4daC
性質
面	18
邊	48
頂點	32
歐拉特徵數	F=18, E=48, V=32 （χ=2）
組成與佈局
面的種類	6個正方形[1] 12個六邊形[2]
頂點佈局 （英语：Vertex_configuration）	(24) 4.6.6 (8) 6.6.6
對稱性
對稱群	Oh（英语：octahedral symmetry）, [4,3], (*432)
旋轉對稱群 （英語：Rotation_groups）	Oh群
特性
凸
圖像
四角化截半立方體 （對偶多面體） （展開圖）
查 论 编

性質

倒角立方體具有偶數邊數的面且180度旋轉對稱的邊，因此可以算作一種環帶多面體，也是一個從立方體不使用膨脹變換構造的一個環帶多面體之一^[4] ，然後又因由正方形和六邊形的面組成，因此也屬於一種八面體對稱的^[5]戈德堡多面體，符號為G_IV(0,2)。此外由於倒角立方體擁有接近正多邊形的面，且有很多面都是正多邊形（六個正方形），因此也是一種擬詹森多面體。

結構

倒角立方體具有18個面、48個邊和32個頂點，由6個正方形和12個六邊形組成^[2]。其結構可視為部分頂點被截去的菱形十二面體，共截去了6個頂點，原本的十二個菱形變為十二個六邊形，截去的頂點變為六個正方形。

由於六邊形是因為切割而產生的，因此是全等，每個邊皆等邊，但不是正六邊形，兩個內角的角度跟原來的菱形十二面體相同，為arccos(-1/3)，約109.47度，而新截出來的四個內角約為125.26度，而正六邊形內角是120度^[6]。

另外一種構造出倒角立方體的方式是由正方體出發，將原本的面擴張，原本的角倒過來，剩下的空隙用六邊形填滿

此外，也可以看作是一種截邊的立方體，即將立方體的十二條邊切去^[7]，切面即變成六邊形，或者是看成將邊以六邊形替代。

倒角立方體可以視為切去所有四階頂點的菱形十二面體，即切去切去相鄰四個面的頂點，因此也稱為截四階角菱形十二面體，有時會簡稱為截角菱形十二面體^[8]，但這種簡稱不合適，因為可能是指倒角八面體^[9]。

另外，倒角立方體也可以視為經過交錯截角的菱形十二面體，即交錯地切除菱形十二面體的頂點，但不是完全切除，因為完全切除會導致原有的菱形面退化成二邊形，即退化為邊，造成結果變為立方體，因此，倒角立方體也可以稱為交錯截角菱形十二面體，同樣，這稱呼存在歧義，因為也可能是指倒角八面體^[9]，不同於交錯的扭稜立方體，其結果僅是兩種手性鏡像，而此例中的結果是倒角八面體以及倒角立方體。

頂點坐標

倒角立方體是菱形十二面體的閔可夫斯基和^[10]，若立方體邊長為一的時候，原本菱形十二面體的八個頂點是位在${\displaystyle (\pm 1,\pm 1,\pm 1)}$，剩餘六個頂點是${\displaystyle (\pm 2,0,0)}$的所有排列組合。

體積與表面積

邊長為a的倒角立方體，其體積為：

${\displaystyle V=a^{3}\times {\biggr (}8+{\frac {40{\sqrt {3}}}{9}}+{\sqrt {\frac {19+8{\sqrt {3}}}{3}}}{\biggr )}\approx 19.0074a^{3}}$.

表面積為：

${\displaystyle A=a^{2}\times {\biggr (}6+8{\sqrt {2}}(1+{\sqrt {3}}){\biggr )}\approx 36.9096a^{2}}$

正方形面的內切球半徑為：

${\displaystyle r_{4}=a\times {\sqrt {\frac {{\frac {19}{2}}+4{\sqrt {3}}}{6}}}\approx 1.6547a}$

六邊形面的內切球半徑為：

${\displaystyle r_{6}=a\times {\biggr (}{\frac {{\sqrt {\frac {8}{3}}}+{\sqrt {2}}}{2}}{\biggr )}\approx 1.5236a}$

倒角倒角立方體

倒角倒角立方體或二次倒角立方體，即進行兩次倒角的立方體，亦可以稱為倒角交錯截角菱形十二面體。

高次倒角立方體

下表列出立方體倒角四次以下的多面體。藍色代表來自於正方體的面、綠色代表經過一次倒角後產生的面、紅色是兩次、紫色是三次、黃色是四次。前幾個的面數是6, 18, 66, 258, 1026, 4098,...... （OEIS數列A178789）、邊數是12, 48, 192, 768, 3072, 12288,...... （OEIS數列A164346）、頂點數是2, 8, 32, 128, 512, 2048, 8192,...... （OEIS數列A004171）。其頂點數皆為二次冪，因此對偶多面體也是2ⁿ面體。此外，這些多面體全部都是戈德堡多面體^[11]。

倒角次數	-1	0	1	2	3	4	n
圖像	多面形	正方體	倒角立方體	倒角倒角立方體	三次倒角立方體	四次倒角立方體	n次倒角立方體
面數	3	6	18	66	258	1026	4n+2
邊數	3	12	48	192	768	3072	3·4n+1
頂點數	2	8	32	128	512	2048	22n+3
戈德堡符號		GIV(0,1)	GIV(0,2)	GIV(0,4)	GIV(0,8)	GIV(0,16)	GIV(0,2n)
對偶多面體	三角形 多邊型二面體	正八面體	四角化截半立方體

相關多面體

拓樸同構體

主条目：立方五角十二面體

倒角立方体有一個對稱性為五角十二面體群的拓樸同構體，其可以透過截去五角十二面體中與座標軸平行的棱構造。這種立體為黃鐵礦的晶形之一。

五角十二面體和其截去與座標軸平行的棱之結果

礦石晶形模型

這種立體也可以視為特殊的切稜立方體，其可以透過切角小於45度且深度大於零的方式切去立方體的稜來構造^[12]。

截角八面體

利用24個倒角立方體堆砌出的截角八面體模型

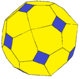
倒角立方體與截角八面體十分類似。

倒角立方體	截角八面體

可以利用24個倒角立方體堆砌出一個截角八面體的模型^[13][14]。

截邊多面體

倒角立方體是立方體透過一種截邊的變換產生的，截邊也可以產生一些不同的多面體，例如：

	（可能的來源）	倒角立方體 （截邊立方體）	截角倒角立方體 （截邊截角立方體）	截半倒角立方體 （截邊截半立方體）	截半立方體
圖像	菱形十二面體	倒角立方體	小斜方截半立方体	大斜方截半立方体	截半立方體
考克斯特符號（英语：Coxeter–Dynkin diagram）
對偶多面體
對偶	截半立方體	四角化截半立方體	鳶形二十四面體	四角化菱形十二面體	菱形十二面體
考克斯特符號（英语：Coxeter–Dynkin diagram）

倒角多面體

倒角立方體是一種正多面體倒角變換結果，其他正多面體或卡塔蘭立體也可以透過倒角變換得到一系列的多面體：

類別	柏拉圖立體					卡塔蘭立體
種子	{3,3}	{4,3}	{3,4}	{5,3}	{3,5}	菱形十二面體	菱形三十面體
倒角	cT	cC	cO（英语：Chamfered octahedron）	cD	cI	caC	caD

多邊形-六邊形鑲嵌

倒角立方體也是一種多邊形-六邊形鑲嵌。

多面體			歐氏鑲嵌	雙曲鑲嵌
三角形-六邊形	四邊形-六邊形	五邊形-六邊形	六邊形-六邊形	七邊形-六邊形
倒角四面體	倒角立方體	倒角十二面體	倒角六邊形鑲嵌	倒角七邊形鑲嵌
截角四面體	截角八面體	截角二十面體	截角六階三角形鑲嵌	截角七階三角形鑲嵌	截角八階三角形鑲嵌

參見

• 立方體
• 菱形十二面體
• 截角菱形十二面體
• 交錯 (幾何)

參考文獻

1. Chamfered Cube Data （页面存档备份，存于互联网档案馆） dmccooey.com [2016-1-17]
2. Sie-Chin Tjong. Nanocrystalline Materials: Their Synthesis-Structure-Property Relationships and Applications. Elsevier. 2006: 117. ISBN 9780080479606. ISBN 008047960X [2016-1-17]
3. Deza, A.; Deza, M.; Grishukhin, V., Fullerenes and coordination polyhedra versus half-cube embeddings, Discrete Mathematics（英语：Discrete Mathematics (journal)）, 1998, 192 (1): 41–80 [2013-03-18], doi:10.1016/S0012-365X(98)00065-X, （原始内容存档于2007-02-06）.
4. 0xDE(11011110) Zonohedra and cubic partial cubes （页面存档备份，存于互联网档案馆） 11011110.livejournal.com 2005-9-6 [2016-1-7]
5. Clinton’s Equal Central Angle Conjecture, JOSEPH D. CLINTON
6. V.A. Zalgaller Convex polyhedra with regular faces Seminar in Mathematics of V. A. Steklov Math. Institute, Leningrad 2 Consultants Bureau, New York (1969)
7. chamferedcube （页面存档备份，存于互联网档案馆） matematicasvisuales.com [2016-1-17]
8. Eppstein, David. The Geometry Junkyard: Zonohedra and Zonotopes. [2016-01-16]. （原始内容存档于2020-03-16）.
9. a truncated form of the rhombic dodecahedron （页面存档备份，存于互联网档案馆） robertlovespi.net 2014-6-9 [2016-1-17]
10. Hazewinkel, Michiel (编), Minkowski addition, 数学百科全书, 施普林格科学+商业媒体, 2001, ISBN 978-1-55608-010-4^{[失效連結]}
11. Hart, George. Goldberg Polyhedra. Senechal, Marjorie (编). Shaping Space 2nd. Springer. 2012: 125–138. doi:10.1007/978-0-387-92714-5_9.
12. 多面体木工. 特定非営利活動法人 科学協力学際センター. 2006-08-01.
13. Gallery of Wooden Polyhedra （页面存档备份，存于互联网档案馆） woodenpolyhedra.web.fc2.com
14. "Wooden polyhedra(English edition)" （页面存档备份，存于互联网档案馆） woodenpolyhedra.web.fc2.com

外部連結

• VTML polyhedral generator（页面存档备份，存于互联网档案馆） Try "t4daC" (康威多面體表示法)
• Zometool model