Комплексная плоскость

Ко́мпле́ксная^[1] пло́скость — геометрическое представление множества комплексных чисел ${\displaystyle \mathbb {C} }$.

Геометрическое представление комплексного числа

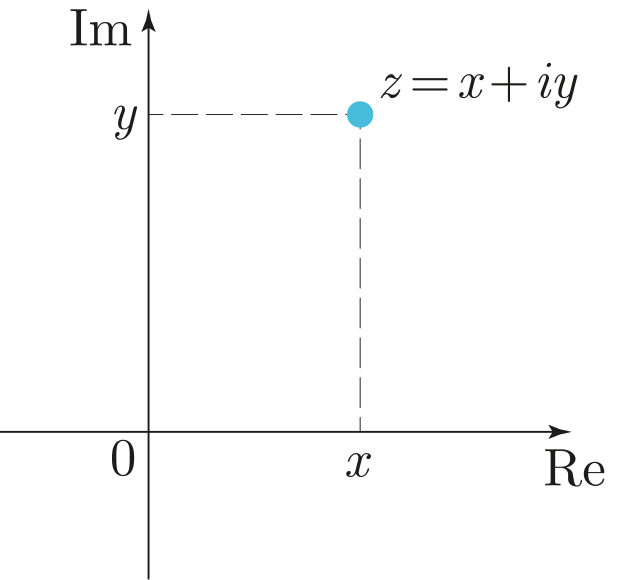
Точка двумерной вещественной плоскости ${\displaystyle \mathbb {R} ^{2}}$, имеющая координаты ${\displaystyle (x,y)}$, изображает комплексное число ${\displaystyle z=x+iy}$, где:

${\displaystyle x=\mathrm {Re} \,z}$ — действительная (вещественная) часть комплексного числа,

${\displaystyle y=\mathrm {Im} \,z}$ — его мнимая часть.

Другими словами, комплексному числу ${\displaystyle z=x+iy}$ соответствует радиус-вектор с координатами ${\displaystyle (x,y).}$ Алгебраическим операциям над комплексными числами соответствуют операции над соответствующими им точками или векторами. Тем самым различные соотношения между комплексными числами получают наглядное изображение на комплексной плоскости:

• сложению комплексных чисел соответствует сложение радиус-векторов;
• умножению на комплексное число ${\displaystyle re^{i\varphi }}$ соответствует поворот радиус-вектора на угол ${\displaystyle \varphi }$ и растяжение радиус-вектора в ${\displaystyle r}$ раз;
• корни n-й степени из числа располагаются в вершинах правильного n-угольника с центром в начале координат.

Комплекснозначные функции комплексного переменного интерпретируются как отображения комплексной плоскости в себя. Особую роль в комплексном анализе играют конформные отображения.

Множества на комплексной плоскости

Открытые множества

Фундаментальное понятие окрестности вводится на комплексной плоскости очень просто — окрестностью ${\displaystyle {\mathcal {U}}_{z_{0}}}$ точки ${\displaystyle z_{0}\in \mathbb {C} }$ называется множество вида ${\displaystyle {\mathcal {U}}_{z_{0}}=\{z\colon |z-z_{0}|<r\},\,r>0}$. Геометрически на комплексной плоскости окрестности имеют очень простой вид — это просто окружности с центром в определенных точках комплексной плоскости. Иногда для удобства требуется рассматривать проколотые окрестности ${\displaystyle {\dot {\mathcal {U}}}_{z_{0}}={\mathcal {U}}_{z_{0}}\setminus \{z_{0}\}}$.

Теперь определим открытое множество — согласно одному из вариантов классического определения из общей топологии, открытым множество будет, если оно для любой своей точки содержит некоторую её окрестность. Определение окрестности у нас уже есть, соответственно, открытое множество на ${\displaystyle \mathbb {C} }$ полностью определено.

Предельная точка и замкнутое множество

Определить предельную точку тоже будет нетрудно — точка ${\displaystyle z_{0}\in \mathbb {C} }$ будет предельной для множества ${\displaystyle G\subset \mathbb {C} }$, если для произвольной окрестности ${\displaystyle {\mathcal {U}}_{z_{0}}}$ пересечение ${\displaystyle {\mathcal {U}}_{z_{0}}\cap G}$ будет не пусто. Другими словами, точка является предельной, если в произвольной «близости» к ней всегда можно будет найти точки множества. Множество предельных точек иногда называется производным и обозначается ${\displaystyle G'}$.

Множество ${\displaystyle G\subset \mathbb {C} }$ будет называться замкнутым, если для него справедливо включение ${\displaystyle G'\subset G}$. Ясно видно, что для произвольного множества ${\displaystyle G}$ множество ${\displaystyle {\overline {G}}=G\cup G'}$ будет замкнуто; оно называется замыканием множества ${\displaystyle G}$.

Граница

Точка ${\displaystyle z_{0}\in \mathbb {C} }$ будет называться граничной для множества ${\displaystyle G\subset \mathbb {C} }$, если для произвольной окрестности ${\displaystyle {\mathcal {U}}_{z_{0}}}$ пересечения ${\displaystyle {\mathcal {U}}_{z_{0}}\cap G}$ и ${\displaystyle {\mathcal {U}}_{z_{0}}\cap ({\mathbb {C} }\setminus G)}$ будут не пусты. Множество всех граничных точек называется граничным множеством ${\displaystyle \partial G}$ или просто границей.

Всюду плотные множества

Множество ${\displaystyle E\subset \mathbb {C} }$ будет называться всюду плотным в ином множестве ${\displaystyle G\subset \mathbb {C} }$, если для произвольной точки ${\displaystyle z_{0}\in G}$ и любой окрестности ${\displaystyle {\mathcal {U}}_{z_{0}}}$ пересечение ${\displaystyle {\mathcal {U}}_{z_{0}}\cap E}$ не пусто.

Связность

Расстояние между множествами

Как известно из элементарной математики, на комплексной плоскости расстояние между двумя точками равно модулю их разности. Теперь определим расстояние между точкой ${\displaystyle z_{0}}$ и некоторым множеством ${\displaystyle G\subset \mathbb {C} }$ как величину ${\displaystyle \mathrm {dist} \,(z_{0},G)=\inf _{z\in G}|z-z_{0}|}$.

На базе этого понятия уже можно определить расстояние между двумя произвольными множествами в ${\displaystyle \mathbb {C} }$: ${\displaystyle \mathrm {dist} \,(G_{1},G_{2})=\inf _{z\in G_{1}}\mathrm {dist} \,(z,G_{2})=\inf _{z\in G_{2}}\mathrm {dist} \,(z,G_{1})}$.

Связность

Множество ${\displaystyle G\subset \mathbb {C} }$ называется связным, если для него выполнено соотношение ${\displaystyle \inf _{z_{1},z_{2}\in G}|z_{1}-z_{2}|=0}$. Если данная величина не равна нулю, то множество называется несвязным. Можно показать, что несвязное множество ${\displaystyle G}$ можно представить в виде объединения (конечного или счетного) ${\displaystyle \sum G_{n}}$, где ${\displaystyle G_{n}}$ — непересекающиеся связные множества, называемые связными компонентами множества ${\displaystyle G}$. Мощность множества связных компонент называется порядком связности.

Выпуклые, звёздные и линейно связные множества

Множество ${\displaystyle G\subset \mathbb {C} }$ называется звёздным относительно точки ${\displaystyle z_{0}\in G}$, если для произвольной точки ${\displaystyle z\in G}$ выполняется включение ${\displaystyle {\overline {z_{0}z}}\subset G}$.

Множество ${\displaystyle G\subset \mathbb {C} }$ называется выпуклым, если оно звёздно относительно любой своей точки. Множество ${\displaystyle G^{*}}$ называется выпуклой оболочкой множества ${\displaystyle G}$, если оно выпукло, ${\displaystyle G\subset G^{*}}$ и для любого выпуклого множества ${\displaystyle G^{**}}$, содержащего множество ${\displaystyle G}$ выполняется включение ${\displaystyle G^{*}\subset G^{**}}$.

Ломаной ${\displaystyle \Gamma }$ называется множество точек комплексной плоскости, представимое в виде объединения отрезков. Множество ${\displaystyle G}$ называется линейно связным, если для двух произвольных точек ${\displaystyle z_{1},z_{2}\in G}$ существует ломаная ${\displaystyle \Gamma \subset G}$ такая, что выполняется ${\displaystyle z_{1},z_{2}\in \Gamma }$.

Можно доказать, что любое линейно связное множество будет связным. Отсюда немедленно следует, что связны все выпуклые и звёздные множества.

Кривые на ℂ

Кривые и пути

Кривой или путём на комплексной плоскости ${\displaystyle \mathbb {C} }$ называется отображение вида ${\displaystyle \varphi (t)\colon [0;1]\to \mathbb {C} }$. Особо стоит отметить, что при таком определении можно конкретизировать не только вид кривой, который будет зависеть от аналитических свойств функции ${\displaystyle \varphi (t)}$, но и её направление. Для примера, функции ${\displaystyle \varphi (t)}$ и ${\displaystyle \eta (t)=\varphi (1-t)}$ будут определять одинаковую по виду кривую, но проходимую в противоположных направлениях.

Гомотопия кривых

Кривые ${\displaystyle \varphi _{0}(t)\colon [0;1]\to \mathbb {C} }$ и ${\displaystyle \varphi _{1}(t)\colon [0;1]\to \mathbb {C} }$ называются гомотопными, если существует кривая ${\displaystyle \xi (t,q)\colon [0;1]\times [0;1]\to \mathbb {C} }$, зависящая от параметра ${\displaystyle q}$ таким образом, что ${\displaystyle \xi (t,0)\equiv \varphi _{0}}$ и ${\displaystyle \xi (t,1)\equiv \varphi _{1}}$.

Аналитическая геометрия на комплексной плоскости

Исследование плоских фигур нередко облегчается, если перенести их на комплексную плоскость. Многие теоремы планиметрии допускают наглядную и компактную запись с помощью комплексных чисел, например^[2]:

• Три (различные) точки ${\displaystyle z_{1},z_{2},z_{3}}$ лежат на одной прямой тогда и только тогда, когда выполняется условие:

${\displaystyle {\frac {z_{1}-z_{3}}{z_{2}-z_{3}}}}$ является вещественным числом.

• Четыре (различные) точки ${\displaystyle z_{1},z_{2},z_{3},z_{4}}$ лежат на одной окружности (или на одной прямой) тогда и только тогда, когда выполняется условие:

отношение ${\displaystyle {\frac {z_{1}-z_{3}}{z_{2}-z_{3}}}:{\frac {z_{1}-z_{4}}{z_{2}-z_{4}}}}$ является вещественным числом.

• Если даны три вершины параллелограмма: ${\displaystyle z_{1},z_{2},z_{3},}$ то четвёртая определяется равенством^[3]: ${\displaystyle z_{4}=z_{1}-z_{2}+z_{3}.}$

Параметрическое уравнение прямой на комплексной плоскости имеет вид^[4]:

${\displaystyle z=ut+v,}$ где ${\displaystyle u,v}$ — комплексные числа, ${\displaystyle u\neq 0,t}$ — произвольный вещественный параметр.

Угол между двумя прямыми ${\displaystyle z=ut+v}$ и ${\displaystyle z=u't+v'}$ равен ${\displaystyle \operatorname {arg} (u'/u).}$ В частности, прямые перпендикулярны, когда ${\displaystyle u'/u}$ — чисто мнимое число. Две прямые параллельны тогда и только тогда, когда ${\displaystyle u'/u}$ есть вещественное число; если при этом ${\displaystyle (v'-v)/u}$ также вещественно, то обе прямые совпадают. Каждая прямая ${\displaystyle z=ut+v}$ рассекает комплексную плоскость на две полуплоскости: на одной из них выражение ${\displaystyle t=\operatorname {Im} {\frac {z-v}{u}}}$ положительно, на другой — отрицательно^[4].

Уравнение окружности с центром ${\displaystyle c}$ и радиусом ${\displaystyle r}$ имеет чрезвычайно простой вид: ${\displaystyle |z-c|=r.}$ Неравенство ${\displaystyle |z-c|<r}$ описывает внутренность окружности^[4]. Часто удобна параметрическая форма уравнения окружности^[5]: ${\displaystyle z=c+e^{i\varphi }.}$

Расширенная комплексная плоскость и бесконечно удалённая точка

В комплексном анализе часто полезно рассматривать расширенную комплексную плоскость^[6], дополненную по сравнению с обычной бесконечно удалённой точкой ${\displaystyle (z=\infty )}$:

${\displaystyle {\widehat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}}$

Геометрически точка ${\displaystyle \infty }$ изображается точкой сферы Римана (её «северный полюс»).

При таком подходе неограниченно возрастающая (по модулю) последовательность считается сходящейся к бесконечно удалённой точке. Алгебраические операции с бесконечностью не производятся, хотя несколько алгебраических соотношений имеют место^[6]:

• ${\displaystyle {\frac {z}{\infty }}=0;\ \ z+\infty =\infty \ (z\neq \infty )}$
• ${\displaystyle z\cdot \infty =\infty$ ;\ \ {\frac {z}{0}}=\infty \ (z\neq 0)}

${\displaystyle \varepsilon }$-окрестностью бесконечно удалённой точки считается множество точек ${\displaystyle z}$, модуль которых больше, чем ${\displaystyle 1 \over \varepsilon }$, то есть внешняя часть ${\displaystyle 1 \over \varepsilon }$-окрестностей начала координат.

Расширенная комплексная плоскость называется также сферой Римана, так как она изоморфна обычной сфере ${\displaystyle S^{2}}$ (изоморфизм можно установить, например, при помощи стереографической проекции). Комплекснозначные функции в некоторых случаях могут быть продолжены на сферу Римана. Поскольку прямые на плоскости (при стереографической проекции) переходят в окружности на сфере, содержащие бесконечно удалённую точку, комплексные функции удобнее рассматривать на сфере.^{[уточнить]}

Преобразования комплексной плоскости

Всякая комплексная функция может рассматриваться как преобразование комплексной плоскости (или как преобразование одной комплексной плоскости в другую). Примеры:

• ${\displaystyle w=z+c}$ — параллельный перенос, определяемый радиус-вектором точки ${\displaystyle c.}$
• ${\displaystyle w=uz,}$ где ${\displaystyle u}$ — комплексное число с единичным модулем, — это поворот вокруг начала координат на угол, равный аргументу ${\displaystyle u;}$
• ${\displaystyle w={\bar {z}}}$ — зеркальное отражение относительно вещественной оси.

Поскольку любое движение на плоскости есть комбинация перечисленных трёх преобразований, функции ${\displaystyle w=uz+c}$ и ${\displaystyle w=u{\bar {z}}+c}$ дают общее выражение для движения на комплексной плоскости^[7].

Другие линейные преобразования^[7]:

• ${\displaystyle w=rz}$, где ${\displaystyle r}$ — положительное вещественное число, задаёт растяжение с коэффициентом ${\displaystyle r}$, если ${\displaystyle r>1,}$ или сжатие в ${\displaystyle {\tfrac {1}{r}}}$ раз, если ${\displaystyle r<1;}$
• преобразования ${\displaystyle w=az+b}$ и ${\displaystyle w=a{\bar {z}}+b,}$ где ${\displaystyle a,b}$ — произвольные комплексные числа, задают преобразование подобия;
• преобразование ${\displaystyle w=az+b{\bar {z}}+c,}$ где ${\displaystyle |a|\neq |b|,}$ — общий вид аффинного преобразования комплексной плоскости (при ${\displaystyle |a|=|b|}$ преобразование не будет аффинным, так как оно будет вырождать плоскость в прямую).

Важную роль в комплексном анализе играют дробно-линейные преобразования^[8]:

${\displaystyle w={\frac {az+b}{cz+d}}.}$

При этом ${\displaystyle ad\neq bc}$ (иначе функция ${\displaystyle w(z)}$ вырождается в константу). Дробно­‑линейные преобразования образуют не­‑абелеву группу. Характеристическое свойство дробно-линейного преобразования: оно переводит окружности и прямые в окружности и прямые (то есть в так называемые обобщённые окружности^[9][10], в число которых входят «окружности бесконечного радиуса» — прямые). При этом образом окружности может оказаться прямая, и наоборот^[8].

Среди других практически полезных функций преобразования: инверсия ${\displaystyle w=1/{\bar {z}},}$ функция Жуковского. Инверсия, как и дробно-линейное преобразование, переводит обобщённые окружности в обобщённые окружности.

В связи с этим плоскость, на которой определены такие преобразования, например, комплексная плоскость в контексте дробно­‑линейных преобразований и инверсий (или комплексных сопряжений) называется круговой плоскостью, а данные преобразования — движениями круговой плоскости (группа движений круговой плоскости). Обычно круговая плоскость рассматривается, будучи расширенной точкой «бесконечность» и топологически представляя собой двумерную сферу, как полярная проекция двумерной сферы на плоскость, расположенную нормально диаметру, на котором лежит полюс сферы, которому ставится в соответствие «бесконечно­‑удалённая точка». Полюс сферы находится вне плоскости. Обобщённым окружностям круговой плоскости при этом взаимно­‑однозначно соответствуют окружности на сфере: прямым — проходящие, окружностям — не проходящие через полюс. Движениям круговой плоскости при таком проецировании соответствуют вращения круговой сферы (группа вращений круговой сферы).

Дробно­‑линейные преобразования при этом соответствуют вращениям (полюс остаётся на месте относительно плоскости, но в него могут попадать другие точки сферы) и сдвигам (горизонтальным и вертикальным) проецируемой сферы (вместе с полюсом), а инверсия — её зеркальному отражению относительно экваториальной плоскости сферы при нахождении полюса сферы на высоте 1 над точкой 0 плоскости (при отражении сферы относительно её экваториальной плоскости происходит инверсия круговой плоскости относительно окружности с центром в проекции полюса на плоскость и радиусом, равным высоте полюса над плоскостью), а так же комбинациям данных простых движений. При этом могут комбинироваться движения, соответствующие разным положениям сферы относительно плоскости, например две последовательные инверсии относительно двух разных окружностей могут быть выполнены путём расположения сферы над центром первой окружности с полюсом на высоте её радиуса, проецированием плоскости на сферу, отражением сферы относительно её экваториальной плоскости, проецированием сферы обратно на плоскость, расположением другой сферы соответственно второй окружности и повторением соответствующих действий уже относительно неё. Уместно заметить, что все описанные действия не зависят от радиуса сферы.

Движения круговой плоскости суть в точности набор всех её автогомеоморфизмов, сохраняющих обобщённые окружности обобщёнными окружностями. Вращения круговой сферы, аналогично, суть в точности набор всех её автогомеоморфизмов, сохраняющих окружности окружностями.

Примечания

1. Двойное ударение указано согласно следующим источникам.

   • Большая советская энциклопедия, 3-е изд. (1973), том 12, стр. 588, статья Ко́мпле́ксные числа.
   • Советский энциклопедический словарь (1982), стр. 613, статья Ко́мпле́ксное число.
   • Последнее издание «Словаря трудностей русского языка» (Розенталь Д. Э., Теленкова М. А., Айрис-пресс, 2005, стр. 273) указывает оба варианта: «ко́мплексные (компле́ксные) числа».
   • В Большой российской энциклопедии (том 14, 2010 год) по необъяснённым причинам предлагаются одновременно ударения Компле́ксное число (стр. 691), но Ко́мплексный анализ (стр. 695).
2. Привалов И. И., 1984, с. 43.
3. Соломенцев Е. Д., 1988, с. 10.
4. Ahlfors Lars V., 1979, с. 17—18.
5. Соломенцев Е. Д., 1988, с. 12.
6. Свешников А. Г., Тихонов А. Н., 1967, с. 20—21.
7. Заславский А. А. Геометрические преобразования. — 2-е изд.. — М.: МЦНМО, 2004. — С. 58. — 86 с. — ISBN 5-94057-094-1.
8. Евграфов М. А., 1968, с. 180—186.
9. MAXimal :: algo :: Преобразование геометрической инверсии  (неопр.). e-maxx.ru. Дата обращения: 9 мая 2021. Архивировано 7 мая 2021 года.
10. Е. А. Морозов, “Обобщённая задача Аполлония”, Матем. просв., сер. 3, 23, Изд-во МЦНМО, М., 2019, 80–111  (неопр.). www.mathnet.ru. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.

Литература

• Арнольд В. И. Геометрия комплексных чисел, кватернионов и спинов, МЦНМО, 2002.
• Евграфов М. А. Аналитические функции. — 2-е изд., перераб. и дополн. — М.: Наука, 1968. — 472 с.
• Понтрягин Л. Комплексные числа, Квант, № 3, 1982.
• Привалов И. И. Введение в теорию функций комплексного переменного. — 13-е изд.. — М.: Физматлит, 1984. — 432 с.
• Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной.. — М.: Наука, 1967. — 304 с.
• Соломенцев Е. Д. Функции комплексного переменногои их применения. — М.: Высшая школа, 1988. — 167 с. — ISBN 5-06-003145-6.
• Шабат Б. В. Введение в комплексный анализ: учебник для студентов механико-математических специальностей университетов, СПб.: 2004.
• Ahlfors Lars V. Complex analysis. An introduction to the theory of analytic functions of one complex variable. — Third edition. — Harvard University: McGraw-Hill Book Company, 1979. — 317 с. — ISBN 0-07-000657-1.