24-celule

În geometrie 24-celule^{[lower-alpha 1]} este un obiect cvadridimensional, un 4-politop convex regulat^[1] (analog cvadridimensional al poliedrelor platonice), cu simbolul Schläfli {3,4,3}. Mai este cunoscut drept octaplex, C₂₄^[2] sau alte denumiri întâlnite în literatura în limba engleză.

24-celule (octaplex)
Diagramă Schlegel (vârfuri și laturi)
Tip	4-politop regulat convex
Simbol Schläfli	{3,4,3} r{3,3,4} = ${\displaystyle \left\{{\begin{array}{l}3\\3,4\end{array}}\right\}}$ {31,1,1} = ${\displaystyle \left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}}$
Diagramă Coxeter	or or
Celule	24 {3,4}
Fețe	96 {3}
Laturi	96
Vârfuri	24
Figura vârfului	Cub
Poligon Petrie	dodecagon
Grup Coxeter	F4, [3,4,3], order 1152 B4, [4,3,3], order 384 D4, [31,1,1], ordinul 192
Dual	autodual
Proprietăți	convex, izogonal, izotoxal, izoedric
Index uniform	22

Desfășurată

Este format din celule octaedrice dintre care câte 6 se întâlnesc în fiecare vârf și câte 3 în fiecare latură. Împreună celulele au 96 de fețe triunghiulare, 96 de laturi și 24 de vârfuri. Figura vârfului este un cub. 24-celule este autodual.^{[lower-alpha 2]} Acesta și tesseractul sunt singurele 4-politopuri convexe regulate la care lungimea muchiei este egală cu raza sferei circumscrise.

24-celule nu are un analog regulat tridimensional. Este singurul dintre cele șase 4-politopuri convexe regulate, care nu este analogul în patru dimensiuni al unuia dintre cele cinci poliedre platonice. Totuși, poate fi văzut ca analogul unei perechi de poliedre neregulate: cuboctaedrul și dualul său, dodecaedrul rombic.

24-celule identice fiind în contact la nivel de fețe pot umple spațiul cvadridimensional, formând fagurele 24-celule. Ca un politop care poate pava prin translație, 24-celule este un exemplu de paralelotop, cel mai simplu care nu este și un zonotop.

Geometrie

24-celule încorporează geometriile fiecărui politop regulat convex din primele patru dimensiuni, cu excepția 5-celule, a celor cu un 5 în simbolul lor Schlӓfli^{[lower-alpha 3]} și a poligoanelor {7} și cu mai multe laturi. Explorarea unui 24-celule este deosebit de utilă deoarece se pot vedea relațiile geometrice dintre toate aceste politopuri regulate într-un singur 24-celule sau fagurele său.

24-celule este al patrulea din secvența de 6 politopuri regulate convexe (în ordinea mărimii și complexității). Politopurile regulate convexe pot fi ordonate după dimensiune ca măsură a conținutului 4-dimensional (hipervolum) pentru aceeași rază. Fiecare politop mai mare din secvență este „mai rotund” decât predecesorul său, cuprinzând mai mult conținut în aceeași rază.^[3] 5-celule (4-simplexul) este cel mai mic, iar 120-celule este cel mai mare. Complexitatea poate fi apreciată comparând matricele configurațiilor lor, sau chiar doar numerele vârfurilor lor.^[4]

Articol principal: 4-politop regulat.

Coordonate

Pătrate

24-celule este anvelopa convexă a vârfurilor sale, care poate fi descrisă de permutările celor 24 de coordonate:

${\displaystyle (\pm 1,\pm 1,0,0)\in \mathbb {R} ^{4}}$.

Aceste coordonate^[5] pot fi generate ca , rectificând 16-celule, , cu permutările a 8 vârfuri (±2,0,0,0). Figura vârfului a 16-celule este octaedrul; astfel, tăierea vârfurilor unui 16-celule la mijlocul laturilor incidente în vârf produce 8 celule octaedrice. Acest proces^[6] produce și rectificarea celulelor tetraedrice ale 16-celule, care devin 16 octaedre, dând cele 24 de celule octaedrice ale 24-celule.

În acest cadru, 24-celule are laturi de lungime √2 și este înscris într-o 3-sferă de rază √2. În mod remarcabil, lungimea muchiei este egală cu raza sferei circumscrise, ca la hexagon, sau cuboctaedru. Astfel de politopuri sunt echilaterale radial.^{[lower-alpha 4]}

Cele 24 de vârfuri formează 18 pătrate mari^{[lower-alpha 5]} (3 seturi de 6 plane ortogonale^{[lower-alpha 6]}), dintre care câte 3 se întâlnesc în fiecare vârf. În fiecare vârf ajunge unul dintre aceste pătrate, astfel că 24-celule poate fi văzut ca vârfurile a 3 perechi de pătrate complet ortogonale^{[lower-alpha 7]} care nu se întâlnesc în niciun vârf^{[lower-alpha 8]}, doar în centrul comun.

Hexagoane

24-celule este autodual, având același număr de vârfuri (24) ca și celulele și același număr de laturi (96) ca și fețele.

Dacă dualul 24-celule cu lungimea laturii √2 este generat pe baza sferei încrise, se obține un alt 24-celule, care are lungimea laturii și raza sferei circumscrise 1, iar coordonatele sale descriu mai bine structura. În acest cadru, 24-celule este poziționat cu un vârf în sus, iar vârfurile sale pot fi obținute după cum urmează:

8 vârfuri obținute prin permutarea coordonatelor întregi:

(±1, 0, 0, 0)

și 16 vârfuri cu coordonate la jumătate de întreg, de forma:

(±1/2, ±1/2, ±1/2, ±1/2)

toate 24 aflându-se la distanța 1 de origine. Aceștia sunt cuaternioni Hurwitz.

În acest sistem de coordonate 24-celule are raza și lungimea laturilor egale cu unitatea^{[lower-alpha 4]}. Acesta diferă de cel cu raza √2 folosit mai sus^{[lower-alpha 9]}

Cele 24 de vârfuri și 96 de laturi formează 16 mari hexagoane neortogonale,^{[lower-alpha 10]} care se intersectează numai în centrul lor comun.^{[lower-alpha 12]} Observând doar un hexagon la fiecare vârf, cele 24-celule poate fi văzut drept cele 24 de vârfuri ale 4 cercurilor mari hexagonale, care nu se intersectează, fiind paralele Clifford unul față de altul.^{[lower-alpha 13]}

Cele 12 axe și 16 hexagoane ale 24-celule constituie o configurație Reye, care în limbajul configurațiilor este scrisă ca 12₄16₃ pentru a indica faptul că fiecare axă aparține a 4 hexagoane și fiecare hexagon conține 3 axe.

Triunghiuri

Cele 24 de vârfuri pot fi văzute ca vârfurile a 8 triunghiuri echilaterale situate^{[lower-alpha 14]} în 4 plane ecuatoriale ortogonale^{[lower-alpha 15]} care se intersectează doar în centrul lor comun.

Coarde hipercubice

Geometria vârfului 24-celulei ehilaterală radial^{[lower-alpha 4]}, care arată cele 3 poligoane înscrise într-un cerc mare și cele 4 lungimi ale coardelor de la vârf la vârf

Cele 24 de vârfuri ale 24-celulei sunt distribuite^[7] la patru diagonale cu lungimi diferite: √1, √2, √3 și √4.

Fiecare vârf este conectat la alte 8. Acestea înconjoară vârful (în spațiul tridimensional al anvelopei 24-celulei), la o distanță de 1, și care subîntind un unghi de 60° = ${\displaystyle {\frac {\pi }{3}}}$, în felul în care cele 8 vârfuri ale unui cub îi înconjoară centrul, figura vârfului 24-celulei fiind un cub.

Următoarele ca distanță sunt 6 vârfuri care înconjoară vârful (în spațiul tridimensional) la o distanță de √2, și care subîntind un unghi de 90° = ${\displaystyle {\frac {\pi }{2}}}$, în felul în care cele 6 vârfuri ale unui octaedru îi înconjoară centrul. Alte 8 vârfuri se află la 120° = ${\displaystyle {\frac {2\pi }{3}}}$, la distanța de √3 pe coarde interioare. Vârful opus este la 180° = ${\displaystyle \pi }$, la distanța de 2, pe diametru. Final, deoarece 24-celule este ehilateral radial, centrul său poate fi considerat^{[lower-alpha 16]} drept un al 25-lea vârf canonic (apex),^{[lower-alpha 17]} fiind la distanța 1 de toate celelalte.

Pentru a vizualiza modul în care sunt aranjate politopurile interioare ale 24-celulei, se observă că cele patru lungimi ale coardelor (√1, √2, √3, √4) sunt diagonalele hipercuburilor din dimensiunile 1 până la 4: diagonala pătratului este √2; cea a cubului este √3; iar cea a tesseractului este √4. Mai mult, diagonala octaedrului este √2 ca a pătratului; iar diagonala 24-celulei este √4 ca a tesseractului. În 24-celule coardele √2 sunt laturile pătratelor centrale, iar coardele √4 sunt diagonalele pătratelor centrale.

Geodezice

Proiecție stereografică a celor 16 hexagoane centrale pe cercurile lor mari. Fiecare cerc mare este divizat de intersecții în 6 laturi arcuite.

Coardele unui 24-celule formează poligoane în cercuri mari geodezice.^{[lower-alpha 19]} Distanța geodezică dintre două vârfuri ale unui 24-celule de-a lungul unei căi cu laturi de √1 este întotdeauna 1, 2 sau 3 și este 3 numai pentru vârfurile opuse.^{[lower-alpha 20]}

Laturile √1 apar în 16 cercuri mari cu hexagoane (în plane înclinate la 60°) din care câte 4 se intersectează^{[lower-alpha 12]}) în fiecare vârf.^{[lower-alpha 11]} Cele 96 de laturi distincte √1 împart suprafața în 96 de fețe triunghiulare și 24 de celule octaedrice: un 24-celule. Cele 16 cercuri mari hexagonale pot fi împărțite în 4 seturi de 4 paralele Clifford care nu se intersectează, astfel încât doar un cerc mare hexagonal din fiecare set să treacă prin fiecare vârf, iar cele 4 hexagoane din fiecare set să atingă toate cele 24 de vârfuri.^{[lower-alpha 13]}

Coardele √2 apar în 18 cercuri mari cu pătrate ^{[lower-alpha 23]} Cele 72 de coardei distincte √2 nu sunt situate în aceleași plane ca cercurile mari cu hexagoane; nu sunt situate pe laturile 24-celulei, trec prin centrele celulelor sale octogonale.^{[lower-alpha 24]} Cele 18 cercuri mari pătratice pot fi împărțite în 3 seturi de 6 geodezice paralele Clifford, ^{[lower-alpha 18]} care nu se intersectează, astfel încât doar un cerc mare pătratic din fiecare set să treacă prin fiecare vârf, iar cele 6 pătrate din fiecare set să ajungă la toate cele 24 de vârfuri.

Coardele √3 apar în 32 de cercuri mari cu triunghiuri în 16 plane (4 seturi de 4 plane ortogonale),^{[lower-alpha 15]} dintre care 4 se intersectează în fiecare vârf.^{[lower-alpha 26]} Cele 96 de coarde distincte √3 merg de la un vârf la oricare alt vârf din aceleași plan al cercurilor mari cu hexagoane.^{[lower-alpha 14]}

Coardele √4 apar ca 12 diametre de la vârf la vârf (3 seturi de 4 axe ortogonale), fiind formate din cele 24 de raze din jurul celui de-al 25-lea vârf central.^{[lower-alpha 17]}

Suma pătratelor lungimilor^{[lower-alpha 27]} tuturor acestor coarde distincte ale 24-celule este 576 = 24^{2/sup>.[lower-alpha 28] Acestea sunt toate poligoanele centrale prin vârfuri, dar în spațiul cvadridimensional există geodezice pe 3-sferă care nu se află deloc în planele centrale. Există căi geodezice cele mai scurte între două vârfuri ale 24-celule care sunt elicoidale, nu circulare; ele corespund unor rotații izoclinice în diagonală, nu rotațiilor simple.[lower-alpha 29]}

Laturile √1 apar în 48 de perechi paralele, la capetele perechilor √3. Coardele √2 apar în 36 de perechi paralele, la capetele perechilor √2. Coardele √3 apar în 48 de perechi paralele, la capetele perechilor √1.^{[lower-alpha 30]}

Planele centrale ale 24-celule pot fi împărțite în 4 hiperplane (tridimensionale) centrale formând fiecare câte un cuboctaedru. Hexagoanele mari sunt la 60° unul de altul; pătratele mari sunt la 90° sau 60° unul de altul; un pătrat mare și un hexagon mare sunt la 90° și 60° unul de altul^{[lower-alpha 33]} Fiecare set de poligoane centrale similare (pătrate sau hexagoane) poate fi împărțit în 4 seturi de poligoane paralele Clifford (din câte 6 pătrate sau 4 hexagoane) care nu se intersectează.^{[lower-alpha 34]} Fiecare set de cercuri mari paralele Clifford este un mănunchi de fibre paralel care trece prin fiecare din cele 24 de vârfuri o singură dată.

Fiecare cerc mare se intersectează^{[lower-alpha 8]} cu celelalte cercuri mari cu care nu sunt paralele Clifford într-un diametru (√4) al 24-celule.{Efn]]^⁠(d) Cercurile mari care sunt complet ortogonale^{[lower-alpha 7]} sau paralele Clifford ^{[lower-alpha 18]} nu se intersectează: ele trec prin seturi de vârfuri disjuncte.^{[lower-alpha 35]}

Construcții

Triunghiurile și pătratele se reunesc în mod unic în 24-celule pentru a genera sub formă de caracteristici interioare ^{[lower-alpha 16]} toate politopurile convexe regulate cu fețe triunghiulare sau pătrate din primele patru dimensiuni, cu excepția a 5-celule și 600-celule.^{[lower-alpha 36]} În consecință, există numeroase moduri de a construi sau descompune un 24-celule.

Construcții alternative din 8-celule și 16-celule

Cele 8 vârfuri întregi (±1, 0, 0, 0) sunt vârfurile unui 16-celule regulat, iar cele 16 vârfuri la jumătate de întreg (±1/2, ±1/2, ±1/2, ±1/2) sunt vârfurile dualului său, tesseractul (8-celule). Tesseractul oferă construcția lui Gosset a 24-celule,^[15] echivalentă cu divizarea tesseractului în 8 piramide cubice, și apoi atașarea acestora la fațetele unui al doilea tesseract. O construcție analoagă în spațiul tridimensional dă dodecaedrul rombic care, totuși, nu este regulat. 16-celule oferă construcția alternativă a 24-celule, construcția lui Cesaro,^[16] echivalentă cu rectificarea unui 16-celule (trunchierea colțurilor sale la mijlocul laturilor, așa cum este descris mai sus). Construcția analogă în 3-spațiu dă cuboctaedrul (dual al dodecaedrului rombic) care nici el nu este regulat. Tesseractul și 16-celule sunt singurele 4-politopuri regulate din 24-celule.^[17]

Se pot împărți în continuare cele 16 vârfuri la jumătate de întreg în două grupuri: cele ale căror coordonate conțin un număr par de semne minus (−) și cele cu un număr impar. Fiecare dintre aceste grupuri de 8 vârfuri definește un 16-celule regulat. Acest lucru arată că vârfurile a 24-celule pot fi grupate în trei seturi disjuncte de opt, fiecare set definind un 16-celule regulat și complementul care definește tesseractul dual.^[18] Acest lucru arată și că simetriile unui 16-celule formează un subgrup cu indice 3 al grupului de simetrie al 24-celule.

Dimininuări

Se poate fațeta 24-celule prin tăierea prin celulele interioare delimitate de coardele dintre vârfuri pentru a îndepărta vârfurile, expunând fațete ale 4-politopurilor interioare înscrise în 24-celule.

Se poate tăia un 24-celule în două părți prin planele oricărui hexagon plan prin 6 vârfuri, a oricărui dreptunghi plan prin 4 vârfuri sau a oricărui triunghi prin 3 vârfuri. Planele cercurilor mari (v. mai sus) sunt doar câteva dintre acele plane. Aici se vor expune unele dintre celelalte: planele fețelor ^{[lower-alpha 37]} politopurilor interioare.^{[lower-alpha 38]}

8-celule

Pornind de la un 24-celule complet, se elimină 8 vârfuri ortogonale (4 perechi opuse pe 4 axe perpendiculare) și cele câte 8 laturi care radiază din fiecare, prin tăierea a 8 celule cubice cu laturi √1, pentru a elimina 8 piramide cubice ale căror apexuri sunt vârfurile care trebuie eliminate. Aceasta elimină câte 4 laturi din fiecare cerc mare cu hexagon (reținând doar o pereche opusă de laturi), astfel încât să nu rămână cercuri mari cu hexagoane continue. Acum, 3 laturi perpendiculare se întâlnesc și formează colțul unui cub în fiecare dintre cele 16 vârfuri rămase,^{[lower-alpha 39]} iar cele 32 de laturi rămase împart suprafața în 24 de fețe pătrate și 8 celule cubice: un tesseract. Există trei moduri în care se poate face acest lucru (se alege câte un set de 8 vârfuri ortogonale din 24), deci există trei astfel de tesseracte înscrise în 24-celule. Se suprapun între ele, dar majoritatea seturilor lor de elemente sunt disjuncte: au în comun un număr de vârfuri, dar nu au lungimea laturii, fețele sau volumul 24-celulei. Ele au în comun 4-nucleul lor comun.^{[lower-alpha 40]}

16-celule

Pornind de la un 24-celule complet, se elimină 16 vârfuri ale unui teseract (reținând cele 8 vârfuri eliminate în cazul de mai sus), prin tăierea a 16 celule tetraedrice mărginite de coarde √2 pentru a elimina 16 piramide tetraedrice ale căror apexuri sunt vârfurile care trebuie eliminate. Aceasta elimină 12 pătrate mari (păstrând doar un set ortogonal) și toate laturile √1, expunând coardele √2 ca noile laturi. Acum restul de 6 pătrate mari se intersectează perpendicular, câte 3 în fiecare dintre cele 8 vârfuri rămase,^{[lower-alpha 41]} iar cele 24 de laturi ale acestora împart suprafața în 32 de fețe triunghiulare și 16 celule tetraedrice: un 16-celule. Există trei moduri în care se poate face acest lucru (se elimină câte unul din seturile de 8 vârfuri ortogonale din 24), deci există trei astfel de 16-celule înscrise în 24-celule. Se suprapun între ele, dar toate seturile lor de elemente sunt disjuncte:^{[lower-alpha 42]} nu au în comun niciun vârf, latură sau față. Ele au în comun 4-nucleul lor comun.^{[lower-alpha 40]}

Construcții tetraedrice

24-celule poate fi construit radial din 96 de triunghiuri echilaterale cu lungimea laturii √1 care se întâlnesc în centrul politopului, fiecare contribuind cu două raze și o latură.^{[lower-alpha 4]} Ele formează 96 de tetraedre (fiecare contribuind cu o față a 24-celulei), toate având în comun al 25-lea vârf central. Acestea formează 24 de piramide octaedrice (semi-16-celule) cu apexurile lor în centru.

24-celule pot fi construite din 96 de triunghiuri echilaterale cu lungimea laturii √2, unde cele trei vârfuri ale fiecărui triunghi sunt situate la 90° = ${\displaystyle {\frac {\pi }{2}}\,}$ departe unul de celălalt. Ele formează 48 de tetraedre √2 (celulele a trei 16-celule).

Relațiile dintre politopurile interioare

24-celule, trei tesseracte și trei 16-celule sunt strâns legate prin centrul lor comun și se intersectează într-un nucleu comun.^{[lower-alpha 40]} Tesseractele sunt înscrise în 24-celule (cele 24 de vârfuri ale 24-celulei, care sunt utilizate fiecare de câte două ori, sunt cele 16 vârfuri a trei tesseracte), astfel încât vârfurile și marginile lor sunt elemente exterioare ale celor 24 de celule, dar fețele pătrate și celulele cubice se află în interiorul 24-celulei (nu sunt elemente ale 24-celulei). Cele trei 16-celule sunt înscrise în 24-celule (cele 24 de vârfuri ale 24-celulei, utilizate fiecare câte o dată, sunt cele 8 vârfuri ale celor trei 16-celule), astfel încât doar vârfurile lor sunt elemente exterioare ale 24-celule: laturile lor, fețele triunghiulare și celulele tetraedrice se află în interiorul 24-celulei. Laturile interioare ale 16-celulelor (laturile 16-celulelor nu sunt afișate în niciuna dintre imaginile din acest articol; dacă s-ar dori prezentarea laturilor interioare, acestea ar putea fi desenate ca linii punctate. Laturile tesseractelor înscrise sunt întotdeauna vizibile, deoarece sunt și laturi ale 24-celulei) au lungimea √2.

Desene ale lui Kepler cu tetraedre înscrise în cub.^[19]

16-celulele sunt înscrise în tesseracte: laturile lor √2 sunt diagonalele fețelor tesseractelor, iar cele 8 vârfuri ale acestora sunt și vârfuri al tesseractelor. Fiecare tesseract are două 16-celule înscrise în el (care ocupă vârfurile și diagonalele opuse), deci fiecare 16-celule este înscris în două dintre cele trei 8-celule.^[20] Acest lucru amintește de modul în care, în 3 dimensiuni, două tetraedre pot fi înscrise într-un cub, așa cum a fost descoperit de Kepler.^[19] De fapt, este analogia dimensională exactă (semihipercuburile), iar cele 48 de celule tetraedrice sunt înscrise în cele 24 de celule cubice exact în acest fel.^[21]

24-celule conține cele trei tesseracte în anvelopa sa de fațete octaedrice, lăsând un spațiu cvadridimensional în unele locuri între anvelopa sa și anvelopele de cuburi al fiecărui tesseract. Fiecare tesseract cuprinde două dintre cele trei 16-celule, lăsând spațiu cvadridimensional în unele locuri între anvelopa sa și anvelopa de tetraedre a fiecărui 16-celule. Astfel există măsurabile:^[22] interstiții cvadridimensionale ^{[lower-alpha 43]} între anvelopele 24-celulei, 8-celulelor și 16-celulelor. Formele care umplu aceste goluri sunt 4-piramide, menționate mai sus.^{[lower-alpha 44]}

Celule de frontieră

În ciuda interstițiilor cvadridimensionale dintre anvelopele 24-celulei, 8-celulelor și 16-celulelor, volumele lor tridimensionale se suprapun. Diferitele anvelope sunt separate în unele locuri și în contact în alte locuri (unde nu există 4-piramide între ele). Unde ele sunt în contact, se îmbină și divizează volumul celulei: sunt aceleași 3-membrane în acele locuri, nu două straturi tridimensionale separate, ci adiacente.^{[lower-alpha 46]} Deoarece există în total 7 anvelope, există locuri în care mai multe anvelope se reunesc și au volume în comun și au locuri în care anvelopele se întrepătrund (se intersectează de la interior la exterior fiecare cu celelalte).

Unele caracteristici interioare se află în spațiul tridimensional (exterior) al anvelopei 24-celulei: fiecare celulă octaedrică este divizată de trei pătrate perpendiculare (câte unul din fiecare tesseract) și diagonalele acelor pătrate (care se intersectează perpendicular unul pe altul în centrul octaedrului) sunt laturi ale 16-celulelor (câte una din fiecare 16-celule). Fiecare pătrat divizează un octaedru în două piramide pătrate și mărginește două celule cubice adiacente ale unui tesseract ca față comună a lor.^{[lower-alpha 45]}

După cum s-a spus mai sus, celulele tetraedrice √2 ale 16-celulelor sunt înscrise în celulele cubice ale tesseractelor √1, având în comun același volum. Celulele octaedrice ale 24-celulei √1 se suprapun în același volum cu celulele cubice √1: sunt divizate de o față pătrată în două piramide pătrate,^[24] apexurile lor fiind în vârfurile cuburilor.^{[lower-alpha 47]} Octaedrele au în comun volumul nu numai cu cuburile, ci și cu tetraedrul înscris în ele; astfel 24-celulele, tesseractele și 16-celulele au toate în comun părți din volumele care le mărginesc.^{[lower-alpha 46]}

Configurație

Matricea de configurație^[25] de mai jos reprezintă un 24-celule. Rândurile și coloanele corespund vârfurilor, laturilor, fețelor și celulelor. Numerele de pe diagonala principală arată câte din fiecare element apar în întregul 24-celule. Celelalte numere arată câte dintre elementele coloanei apar în sau la elementul rândului.

${\displaystyle {\begin{bmatrix}{\begin{matrix}24&8&12&6\\2&96&3&3\\3&3&96&2\\6&12&8&24\end{matrix}}\end{bmatrix}}}$

Deoarece 24-celule este autodual, matricea sa este identică cu cea rotită cu 180°.

Simetriile, sistemele de vectori generatori și teselările

Compusul cu 24 de vârfuri ale 24-celule (nodurile roșii) și dualul său nescalat (nodurile galbene), reprezintă cei 48 de vectori generatori ai grupului F₄, așa cum se arată în această proiecție în planul Coxeter a F₄

Cei 24 de vectori generatori ai sistemului de generatori ai D₄ din grupul Lie simplu SO(8) formează vârfurile unui 24-celule. Vârfurile pot fi văzute în 3 hiperplane,^{[lower-alpha 31]} câte 6 vârfuri ale celor două celule octaedrice, câte una pe fiecare dintre hiperplanele exterioare și cele 12 vârfuri ale unui cuboctaedru pe un hiperplan central. Aceste vârfuri, combinate cu cele 8 vârfuri ale 16-celule, reprezintă cei 32 de vectori generatori ai grupurilor Lie simple B₄ și C₄.

Cele 48 de vârfuri (sau strict vorbind vectorii razelor lor) ale reuniunii 24-celulei și a dualului său formează sistemul de generatori de tipul F₄.^[27] Cele 24 de vârfuri ale 24-celule inițial formează un sistem de generatori de tip D₄; dimensiunea sa are raportul √2:1. Acest lucru este valabil și pentru cele 24 de vârfuri ale dualului său. Grupul de simetrie complet al 24-celule este grupul Weyl al lui F₄, care este generat de reflexiile pe hiperplanele ortogonale ale generatorilor F₄. Acesta este un grup rezolvabil de ordinul 1152. Grupul de simetrie de rotație al 24-celule este de ordinul 576.

Interpretare cuaternionică

Cele 24 de elemente ale cuaternionilor grupului tetraedric binar, 2T, corespund vârfurilor 24-celulei.
În proiecția simetriilor 4-pliabile există:
* 1 de ordinul 1:   1
* 1 de ordinul 2: −1
* 6 de ordinul 4: ±i, ±j, ±k
* 8 de ordinul 6: (+1, ±i, ±j, ±k)/2
* 8 de ordinul 3: (−1, ±i, ±j, ±k)/2.

Când este interpretat prin cuaternioni, laticea generatorilor F₄ (care este generarea integrală a vârfurilor unui 24-celule) este un inel. Acesta este inelul cuaternionilor Hurwitz. Vârfurile unui 24-celule formează grupul de unități (adică grupul de elemente inversabile) din inelul de cuaternioni Hurwitz (acest grup este, de asemenea, cunoscut sub numele de grupul tetraedric binar). Vârfurile unui 24-celule sunt tocmai cei 24 de cuaternioni Hurwitz cu norma pătrată 1, iar vârfurile unui 24-celule sunt cele cu norma pătrată 2. Laticea generatorilor D₄ este duala celei a F₄ și este dată de subinelul cuaternionilor Hurwitz cu normă pătrată.

Privite ca cei 24 de cuaternioni Hurwitz unitate, coordonatele razei unitare ale 24-celule reprezintă (în perechi de antipode) cele 12 rotații ale unui tetraedru regualt.^[28]

Vârfurile altor 4-politopuri regulate convexe formează, de asemenea, grupuri multiplicative de cuaternioni, dar puține dintre ele generează o latice de generatori.

Celule Voronoi

Celulele Voronoi ale laticei generatorilor D₄ sunt 24-celule regulate. Teselarea Voronoi corespunzătoare dă teselarea 4-dimensională a spațiului euclidian cu 24-celule regulate, fagurele 24-celule. 24-celulele sunt centrate în punctele laticei D₄ (cuaternionii Hurwitz cu normă pătrată pară) în timp ce vârfurile sunt în punctele laticei F₄ cu normă pătrată impară. Fiecare 24-celule ale acestei teselări are 24 de vecini. Cu fiecare dintre aceștia are în comun un octaedru. De asemenea, are alți 24 de vecini cu care are în comun doar un singur vârf. Opt 24-celule se întâlnesc în orice vârf din această teselare. Simbolul Schläfli pentru această teselare este {3,4,3,3}. Este una dintre cele trei teselări regulate ale R⁴.

Bila unitate înscrisă în 24-celule ale acestei teselări dă naștere celei mai dense împachetări a hipersferelor din 4 dimensiuni. De asemenea, s-a arătat că configurația vârfului 24-celulei dă cel mai mare număr de contacte în 4 dimensiuni.

Fagure radial echilateral

Duala teselării fagurelui 24-celule {3,4,3,3} este fagurele 16-celule {3,3,4,3}. A treia teselare regulată a spațiului cvadridimensional este fagurele tesseractic {4,3,3,4}, ale cărui vârfuri pot fi descrise prin coordonate carteziene cu 4 numere întregi. Relațiile congruente dintre aceste trei teselări pot fi utile în vizualizarea unui 24-celule, în special a simetriei echilaterale radiale pe care are în comun cu tesseractul.^{[lower-alpha 4]}

Un fagure 24-celule cu lungimea laturii unitate poate fi suprapus pe un fagure tesseractic cu lungimea laturii unitate astfel încât fiecare vârf al unui tesseract (fiecare coordonată de 4 numere întregi) să fie, de asemenea, un vârf al unui 24-celule (laturile tesseractelor sunt și laturile 24-celuleilor) și fiecare centru al unui 24-celule este, de asemenea, centrul unui tesseract.^[29] 24-celulele au în 4 dimensiuni un hipervolum de două ori mai mare ca tesseractele, deci în general există două tesseracte pentru fiecare 24-celule, dintre care doar jumătate sunt înscrise într-un 24-celule. Dacă tesseractele respective sunt colorate în negru, iar tesseractele lor adiacente (cu care împart o fațetă cubică) sunt colorate în roșu, rezultă o tablă de șah 4-dimensională.^[30] Dintre razele fiecărui 24-celule^{[lower-alpha 48]} 16 sunt șirazele unui tesseract negru înscris în 24-celule. Celelalte 8 raze se extind în afara tesseractului negru (prin centrele fațetelor sale cubice) până la centrele celor 8 tesseracte roșii adiacente. Astfel fagurele 24-celule și fagurele tesseractic coincid într-un mod special: 8 din cele 24 de vârfuri ale fiecărui 24-celule nu apar ca vârfuri al unui tesseract (ele apar în schimb în centrul unui tesseract). Fiecare tesseract negru este tăiat dintr-un 24-celule prin trunchierea acestuia la aceste 8 vârfuri, fiind tăiate 8 piramide cubice (ca în cazul inversării construcției lui Gosset,^[15] dar în loc să fie eliminate, piramidele sunt pur și simplu colorate în roșu și lăsate la locul lor). Opt 24-celule se întâlnesc în centrul fiecărui tesseract roșu: fiecare își întâlnește opusul în acel vârf comun, iar celelalte șase într-o celulă octaedrică comună.

Tesseractele roșii sunt celule umplute (conțin un vârf central și raze); tesseractele negre sunt celule goale. Setul de vârfuri al acestei reuniuni de doi faguri include vârfurile tuturor acelor 24-celule și tesseracte, plus centrele tesseractelor roșii. Adăugarea centrelor 24-celulelor (care sunt, de asemenea, centrele tesseractelor negre) la acest fagure produce un fagure 16-celule, al cărui set de vârfuri include toate vârfurile și centrele tuturor acelor 24-celule și tesseracte. Fostele centre goale al 24-celulelor adiacente devin vârfurile opuse ale 16-celulelor cu latura unitate. 24 de semi-16-celule (piramide octaedrice) se întâlnesc în fiecare centru anterior gol pentru a umple fiecare 24- celule, iar bazele lor octaedrice sunt fațetele octaedrice cu 6 vârfuri ale 24-celulei (partajate cu un 24-celule adiacent).^{[lower-alpha 49]}

De observat absența completă a pentagoanelor oriunde în această reuniune de trei faguri. La fel ca 24-celule, spațiul euclidian cvadridimensional este umplut el însuși în întregime de un complex de toate politopurile care pot fi construite din triunghiuri regulate și pătrate (cu excepția 5-celule), dar acel complex nu necesită (sau permite) niciunul dintre politopurile pentagonale.^{[lower-alpha 3]}

Rotații

4-politopurile convexe regulate sunt o expresie a simetriei care este cunoscută sub numele de grup de rotații SO(4) în jurul unui punct fix în spațiul euclidian cvadridimensional.^{[lower-alpha 50]}

Cele 3 baze carteziene ale 24-celule

Există trei orientări diferite ale fagurelui tesseractic care ar putea fi făcut să coincidă cu fagurele 24-celule în funcție de care dintre cele trei seturi disjuncte de 24-celule de 8 vârfuri ortogonale (care setează 4 axe perpendiculare, sau, echivalent, cu 16-celule înscrise) a fost ales pentru a-l alinia, la fel cum se pot înscrie trei tesseracte în 24-celule, rotite unul față de celălalt. Distanța de la una dintre aceste orientări la alta este o rotație izoclinică de 60° (o rotație dublă de 60° de grade în fiecare pereche de plane ortogonale invariante, în jurul unui singur punct fix).^{[lower-alpha 50]} Această rotație poate fi văzută cel mai clar în planele centrale cu hexagoane, unde hexagonul se rotește pentru a schimba care dintre cele trei diametre ale sale este aliniat cu o axă a sistemului de coordonate.^{[lower-alpha 10]}

Setul de vârfuri al 24-celule este grupul tetraedric binar. Privite ca cei 24 de cuaternioni Hurwitz unitate, [#Hexagoane|coordonatele razei unitate]] a 24-celule reprezintă (în perechi antipodale) cele 12 rotații ale unui tetraedru regulat.^[28]

Plane de rotație

Rotațiile în spațiul euclidian cvadridimensional pot fi văzute drept compunerea a două rotații bidimensionale în plane complet ortogonale.^[32] Astfel, rotația generală în spații cvadridimensionale este o rotație dublă. Există două cazuri particulare importante, numite rotație simplă și rotație izoclinică.^{[lower-alpha 56]}

Rotații simple

Proiecție 3D a unui 24-celule executând o rotație simplă

În spațiul tridimensional, un poliedru care se învârte are un singur plan de rotație, central, invariant. Se spune că planul este invariant deoarece fiecare punct din plan se mișcă pe un cerc dar rămân în plan. Doar unul din planele centrale ale poliedrului poate fi invariant în timpul unei anumite rotații. Alegerea planului central invariant și unghiul cu care este rotit definește complet rotația. Punctele din afara planului invariant se mișcă, de asemenea, în cercuri (cu excepția cazului în care sunt pe axa de rotație fixă perpendiculară pe planul invariant), dar cercurile nu se află într-un plan central.

Când un 4-politop se rotește cu un singur plan central invariant, se efectuează o rotație simplă care are loc în spațiul tridimensional. Singura diferență este că în loc de o axă fixă de rotație, există un întreg plan central fix în care punctele nu se mișcă. Planul fix este singurul plan central care este complet ortogonal^{[lower-alpha 7]} cu planul invariant de rotație. 24-celule va efectua o rotație simplă care va duce orice vârf la orice alt vârf, deplasând și majoritatea celorlalte vârfuri, dar lăsând cel puțin 2 și cel mult 6 vârfuri fixe (vârfurile pe care le intersectează planul central fix). Vârful se mișcă de-a lungul unui cerc mare în planul invariant de rotație, prin vârfurile adiacente ale unui hexagon mare, a unui pătrat mare sau a unui digon mare, iar planul fix complet ortogonal este un digon, un pătrat, respectiv un hexagon.^{[lower-alpha 35]}

Rotații duble

Proiecție 3D a unui 24-celule executând o rotație dublă

Punctele din planul central complet ortogonal nu sunt constrânse să fie fixe. De asemenea, este posibil ca acestea să se rotească în cercuri dintr-un al doilea plan invariant, cu o viteză de rotație independentă de viteza rotației în primul plan invariant: o rotație dublă simultană.^{[lower-alpha 54]} Într-o rotație dublă nu există un plan sau o axă fixă: fiecare punct se mișcă, cu excepția punctului central. Unghiul de rotație poate fi diferit în cele două plane centrale complet ortogonale, dar ambele sunt întotdeauna invariante: punctele lor care se mișcă în cerc rămân în plan pe măsură ce întregul plan se înclină lateral în rotația complet ortogonală. O rotație în 4-spațiu are întotdeauna (cel puțin) două plane de rotație invariante complet ortogonale, deși într-o rotație simplă unghiul de rotație într-unul din ele este 0.

Rotațiile duble au două forme chirale: rotații la stânga și la dreapta. Într-o rotație dublă, fiecare vârf se mișcă în spirală simultan de-a lungul a două cercuri mari complet ortogonale.^{[lower-alpha 53]} Fie calea este pe dreapta (în sensul unui filet, ca majoritatea șuruburilor), deplasându-se de-a lungul cercurilor în aceleași direcții, fie este pe stânga (ca la un șurub cu filet pe stânga), deplasându-se de-a lungul cercurilor în ceea ce spunem în mod convențional că sunt direcții opuse (conform regulii mâinii drepte prin care în mod convențional se spune ce direcție este în sus pe fiecare dintre cele 4 axe de coordonate).

Rotații izoclinice

Când unghiurile de rotație în cele două plane invariante sunt exact aceleași, apare o transformare geometrică remarcabil de simetrică: toate planele cercurilor mari paralele Clifford^{[lower-alpha 18]} cu planele invariante devin ele însele plane de rotație invariante cu același unghi, iar 4-politopul se rotește izoclinic în mai multe direcții simultan.^[34] Fiecare vârf se mișcă la o distanță egală în două direcții ortogonle simultan.^{[lower-alpha 57]} Într-un 24-celule orice rotație izoclinică de 60° într-un plan hexagonal mută fiecare vârf în poziția unui vârf învecinat, rotește toate cele 16 hexagoane cu 60° și mută fiecare cerc mare poligonal (pătrat,^{[lower-alpha 32]} hexagon sau triunghi) la un cerc mare poligonal paralel Clifford de același fel la 60° distanță. O rotație izoclinică mai este numită și deplasare Clifford, după descoperitor.^{[lower-alpha 55]}

În animația de rotație dublă 24-celule pare să se întoarcă pe dos.{Efn|Că o rotație dublă poate întoarce un 4-politop pe dos este foarte vizibil într-o dublă rotație a unui tesseract.}} Se pare că, pentru că de fapt o face, inversează chiralitatea întregului 4-politop exact așa cum o oglindă inversează chiralitatea unei imagini printr-o reflexie la 180°. Fiecare rotație izoclinică de 360° este de parcă suprafața 24-celule ar fi fost scoasă ca o mănușă și pusă pe dos, făcând dintr-o mănușă „dreapta” o mănușă „stânga” (sau invers, în funcție de faptul că a fost o rotație izoclinică de 360° la stânga sau la dreapta).

Într-o rotație simplă a 24-celule într-un plan hexagonal, fiecare vârf din plan se rotește mai întâi de-a lungul unei laturi până la un vârf adiacent aflat la 60° distanță. Dar într-o rotație izoclinică în două plane complet ortogonale, dintre care unul este hexagonal mare,^{[lower-alpha 35]} fiecare vârf se rotește mai întâi la un vârf la două lungimi de latură distanță (diagonală) într-un plan hexagonal diferit.^{[lower-alpha 58]} Geodezicele elicoidale dublu rotite cu 60° trec prin fiecare alt vârf, oscilând între planele centrale hexagonale.^{[lower-alpha 53]} Chiar dacă toate vârfurile și toate hexagoanele se rotesc deodată, rotația izoclinică de 360° afectează doar jumătate din vârfurile unei 24-celule. După 360° fiecare elice a trecut prin 6 vârfuri, dar nu a ajuns înapoi la vârful din care a plecat pentru a forma un hexagon închis. Fiecare plan central (fiecare hexagon sau pătrat al 24-celule) s-a rotit cu 360° și până la poziția inițială a fost înclinat lateral înapoi cu 360°, orientarea 24-celule în spațiul cvadridimensional în care este încorporat este acum diferită. De observat cum 24-celule din animația cu rotația dublă pare să se întoarcă pe dos. Deoarece 24-celule este acum cu interiorul spre exterior, dacă rotația izoclinică este continuată în aceeași direcție cu alte 360°, vârfurile în mișcare vor trece prin cealaltă jumătate de vârfuri pe care le-au omis la prima revoluție (vârfurile antipodale celor prin care au trecut la prima rotație) și fiecare geodezică izoclinică va ajunge înapoi la vârful din care a plecat, formând un dodecagon închis.^{[lower-alpha 59]} Este nevoie de o rotație izoclinică de 720° pentru ca fiecare geodezică izoclinică dodecagonală să finalizeze prin două înconjurări a politopului 24-celule un circuit prin toate cele 12 vârfuri aflate pe ea și a readuce 24-celule la orientarea chirală inițială.^[35]

Calea de înfășurare dodecagonală pe care o urmează fiecare vârf în timp ce se învârte de două ori în jurul 24-celule formează o spirală dublă răsucită într-un Inel Möbius, astfel încât cele două fire ale elicei duble formează un singur fir continuu într-un buclă închisă. În prima revoluție vârful parcurge un fir al dublei elice prin 6 vârfuri; în a doua revoluție îl parcurge pe al doilea, paralel Clifford,^{[lower-alpha 18]} mișcându-se în aceeași direcție de rotație și în aceeași manieră (îndoindu-se fie la stânga, fie la dreapta) peste tot. Deși această cale izoclinică este o spirală închisă, nu un cerc mare bidimensional, este o geodezică, deoarece este cea mai scurtă cale de la un vârf la altul.^{[lower-alpha 29]}

Două plane se mai numesc izoclinice dacă o rotație izoclinică le va aduce împreună.^{[lower-alpha 33]} Planele izoclinice sunt tocmai acele planuri centrale cu geodezice cercuri mari paralele Clifford.^[36] Cercurile mari paralele Clifford nu se intersectează, astfel încât poligoanele cercurilor mari izoclinice au vârfuri disjuncte. În 24-celule, fiecare plan central hexagonal este izoclinic cu alte trei, iar fiecare plan central pătratic este izoclinic cu alte cinci. ^{[lower-alpha 25]} Se pot alege 4 hexagoane mari reciproc izoclinice (paralele Clifford, patru moduri diferite) care acoperă toate cele 24 de vârfuri ale 24-celule o singură dată. Se pot alege 6 pătrate mari reciproc izoclinice (paralele Clifford, trei moduri diferite) care acoperă toate cele 24 de vârfuri ale 24-celule o singură dată. ^{[lower-alpha 13]}

Politopuri paralele Clifford

Poligoanele bidimensionale dintr-un cerc mare nu sunt singurele politopuri din 24-celule care sunt paralele în sens Clifford.^[37] Politopurile congruente din 2, 3 sau 4 dimensiuni se poate spune că sunt paralele Clifford în 4 dimensiuni dacă vârfurile lor corespunzătoare sunt toate la aceeași distanță. Cele trei 16-celule înscrise în 24-celule sunt paralele Clifford. Politopurile paralele Clifford sunt complet disjuncte.^{[lower-alpha 42]} O rotație izoclinică de 60° în planele hexagonale duce fiecare 16-celule la un 16-celule disjunct. Ca toate rotațiile duble, rotațiile izoclinice au două forme chirale: există câte un 16-celule disjunct la stânga fiecărui 16-celule și altul la dreapta acestuia.

Toate 4-politopurile paralele Clifford sunt legate printr-o rotație izoclinică,^{[lower-alpha 55]} dar nu toate politopurile izoclinice sunt paralele Clifford (complet disjuncte). ^{[lower-alpha 60]} Cele trei 8-celule din 24-celule sunt izoclinice, dar nu paralele Clifford. Ca și la 16-celule, ele sunt rotite izoclinic la 60° unele față de altele, dar vârfurile lor nu sunt toate disjuncte (prin urmare nu sunt toate echidistante). Fiecare vârf apare în două dintre cele trei 8-celule (deoarece fiecare 16-celule apare în două dintre cele trei 8-celule).

Rotațiile izoclinice leagă 4-politopurile regulate convexe între ele. O rotație izoclinică a unui singur 16-celule va genera^{[lower-alpha 61]} un 24-celule. O rotație simplă a unui singur 16-celule nu va genera, deoarece vârfurile sale nu vor atinge niciunul dintre vârfurile celorlalte două 16-celule în cursul rotației. O rotație izoclinică a unui 24-celule va genera un 600-celule, iar o rotație izoclinică a unui 600-celule va genera un 120 de celule. (Sau toate pot fi generate direct de rotațiile izoclinice ale 16-celule, generând copii izoclinice ale lui însuși.) 4-politopurile regulate convexe se imbrică unul în altul și se ascund unul lângă altul, în spațiile paralele Clifford, inclusiv 3-sfera. Pentru un obiect cu mai mult de o singură dimensiune, singura modalitate de a ajunge direct în aceste subspații paralele este prin rotație izoclinică.^{[lower-alpha 62]}

Proiecții

Proiecții paralele

Proiecții ale anvelopei unui 24-celule; fiecare celulă are fețele colorate diferit, celulele inversate nu sunt redate

Proiecția paralelă cu un vârf în față a anvelopei unui 24-celule în spațiul tridimensional este un dodecaedru rombic. Douăsprezece din cele 24 de celule octaedrice se proiectează în perechi pe șase dipiramide pătrate care se întâlnesc în centrul dodecaedrului rombic. Celelalte 12 celule octaedrice se proiectează pe cele 12 fețe rombice ale dodecaedrului rombic.

Proiecția paralelă cu o celulă în față a anvelopei unui 24-celule este un cuboctaedru. Două dintre celulele octaedrice, cea mai apropiată și mai îndepărtată de-a lungul axei w, se proiectează pe un octaedru ale cărui vârfuri se află în centrul fețelor pătrate ale cuboctaedrului. În jurul acestui octaedru central se află proiecțiile altor 16 celule, formând 8 perechi care se proiectează pe unul dintre cele 8 volume situate între o față triunghiulară a octaedrului central și cea mai apropiată față triunghiulară a cuboctaedrului. Restul de 6 celule se proiectează pe fețele pătrate ale cuboctaedrului. Acest lucru corespunde descompunerii cuboctaedrului într-un octaedru regulat și 8 octaedre neregulate, dar egale, fiecare dintre acestea având forma anvelopei convexe a unui cub cu două vârfuri opuse îndepărtate.

Proiecția paralelă cu o latură în față a anvelopei unui 24-celule este o bipiramidă hexagonală alungită, iar proiecția paralelă cu o față în față a anvelopei unui 24-celule este o biantiprismă hexagonală.

Proiecții în perspectivă

Proiecția în perspectivă cu un vârf în față a anvelopei unui 24-celule în spațiul tridimensional este un hexaedru tetrakis. Aspectul celulelor din această imagine este similar cu imaginea în proiecție paralelă.

Următoarele imagini arată structura proiecției tridimensionale în perspectivă cu o celulă în față a unui 24-celule. Punctul de vedere 4D este amplasat la o distanță de cinci ori mai mare decât raza centrului vârfului 24-celulei.

Proiecție în perspectivă cu o celulă în față
În această imagine, cea mai apropiată celulă este cea colorată roșu, iar celelalte celule sunt pe contur. Pentru claritate, celulele care se îndreaptă în altă direcție decât punctul de vedere 4D au fost eliminate.	În această imagine, patru dintre cele 8 celule care înconjoară cea mai apropiată celulă sunt colorate verde. Văzută din punctul de vedere a patra celulă se află în spatele celulei centrale (ușor sesizabilă, deoarece celula roșie este semitransparentă).	Aici sunt afișate toate cele 8 celule care înconjoară cea mai apropiată celulă, ultimele patru fiind colorate violet.
Aceste imagini nu redau celulele care se îndreaptă în altă direcție decât spre punctul de vedere 4D. Prin urmare, aici sunt afișate doar 9 celule. Pe partea îndepărtată a 24-celulei sunt alte 9 celule într-un aranjament identic. Restul de 6 celule se află pe ecuatorul 24-celulei, fiind în contact cu cele două seturi de celule.

Alte proiecții

Proiecție stereoscopică 3D a unui 24-celule

Secțiune animată printr-un 24-celule

Proiecții ortogonale

Proiecții ortogonale

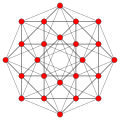
Plan Coxeter	F4	B3 / A2 (a)	B3 / A2 (b)	B4	B2 / A3
Graf
Simetrie diedrală	[12]	[6]	[6]	[8]	[4]

Vizualizări

Octacube, sculptură din oțel de Adrian Ocneanu, la Pennsylvania State University, o poiecție în 3D a 24-celule

Un 24-celule este delimitat de 24 de celule octaedrice. În scopul vizualizării, este convenabil ca octaedrul să aibă fețele opuse paralele (elemente pe care le are în comun cu celulele tesseractelor și ale 120-celule). Se pot stivui octaedre față în față într-o linie dreaptă îndoită în a 4-a direcție într-un cerc mare cu o circumferință de 6 celule. Pozițiile celulelor corespund unei descrieri hipersferice. Fie o celulă arbitrară etichetată „polul nord”. Opt cercuri mari meridiane (lungi de două celule) se desfășoară în 3 dimensiuni radial, convergând spre o a 3-a celulă „polul sud”. Acest schelet reprezintă 18 din cele 24 de celule (2 + 8×2). Vezi tabelul de mai jos.

Într-un 24-celule există un alt cerc mare, dualul celui de mai sus. O cale care traversează 6 vârfuri numai de-a lungul laturilor se află în dualul acestui politop, care este el însuși, deoarece este autodual. Acestea sunt geodezice hexagonale descrise mai sus.^{[lower-alpha 13]} Se poate urmări cu ușurință această cale într-o redare a secțiunii ecuatoriale cuboctaedrice.

Începând de la polul nord, un 24-celule poate fi construit în 5 straturi pe latitudine. Cu excepția polilor, fiecare strat reprezintă o 2-sferă separată, ecuatorul fiind o mare 2-sferă. Celulele etichetate ecuatorial în tabelul următor se află în interstițiile dintre celulele cercurilor mari meridiane. Celulele „ecuatoriale” ating celulele meridiane cu care sunt în contact pe fețele lor. Se ating unele pe celelalte, iar celulele polare le ating în vârfurile lor. Acest ultim subset de opt celule polare și nemeridiane are aceeași poziție relativă ca și celulele dintr-un tesseract, deși se ating doar la vârfuri în loc de fețe.

O proiecție în perspectivă cu o latură în față, care arată unul din cele patru inele de 6 octaedre din jurul ecuatorului

Nr. stratului	Nr. celulelor	Descriere	Latitudine	Regiune
1	1 celulă	„Polul nord”	0°	Emisfera nordică
2	8 celule	Primul strat de celule meridiane	60°
3	6 celule	Nemeridian / interstițial	90°	Ecuator
4	8 celule	Al doilea strat de celule meridiane	120°	Emisfera sudică
5	1 celulă	Polul sud	180°
Total	24 celule

Cele 24 de celule pot fi împărțite în patru seturi disjuncte de inele din 6 celule aflate în cercuri mari, formând o fibrare Hopf discretă din patru inele interconectate.^[38] Un inel este „vertical”, cuprinzând celulele pol și patru celule meridiane. Celelalte trei inele cuprind fiecare două celule ecuatoriale și patru celule meridiane, două din emisfera nordică și două din cea sudică.

De reținut că această cale hexagonală a cercului mare implică un unghiul interior/diedru dintre celulele adiacente de 180 – 360/6 = 120°. Acest lucru sugerează că se pot plasa adiacent exact trei 24-celule într-un plan și se poate forma un fagure cvadridimensional din 24-celule, așa cum a fost descris anterior.

Se poate urmări, de asemenea, o cale pe un cerc mare prin vârfurile opuse ale octaedrelor, cale care are o lungime de patru celule. Acestea sunt geodezicele pătrate de-a lungul a patru coarde √2. Această cale corespunde traversării diagonale prin pătratele din secțiunea transversală a cuboctaedrului. 24-celule este singurul politop regulat în mai mult de două dimensiuni în care se poate traversa un cerc mare doar prin vârfurile opuse (și interiorul) fiecărei celule. Acest cerc mare este autodual. Această cale a fost urmată mai sus prin setul de 8 celule nemeridiane (ecuatoriale) și polare. 24-celule poate divizat în trei subseturi de 8 celule, fiecare având organizarea unui tesseract. Fiecare dintre aceste subseturi poate fi divizat în continuare în două lanțuri de cercuri mari de patru celule, care se întrepătrund. Împreună, aceste trei subseturi produc acum o altă fibrare Hopf discretă cu șase inele.

Construcția a trei grupuri Coxeter

Există două forme inferioare de simetrie ale 24-celulei: simetria B₄ sau [3,3,4], obținută prin rectificarea unui 16-celule, simetrie cu 8 și 16 celule octaedrice, colorate în două culori, și simetria D₄ sau [3^1,1,1] obținută prin rectificarea unui semitesseract, simetrie cu câte 8 octaedre, colorate în trei culori.

Trei desfășurate ale 24-celule cu celulele colorate conform simetriilor D4, B4 și F4
Semitesseract rectificat	16-celule rectificat	24-celule regulat
D4, [31,1,1], ordin 192	B4, [3,3,4], ordin 384	F4, [3,4,3], ordin 1152
Trei seturi de 8 celule tetraedrice rectificate	Un set de 16 celule tetraedrice rectificate și unul de 8 celule octaedrice	Un set de 24 celule octaedrice
Figura vârfului (Fiecare latură corespunde unei fețe triunghiulare, colorate după simetrii)

Poligoane complexe asociate

Poligonul complex regulat ₄{3}₄, sau conține cele 24 de vârfuri ale unui 24-celule, și 24 de 4-laturi care corespund pătratelor din centrele a 24 din cele 48 de celule octaedrice. Simetria sa este ₄[3]₄, ordinul 96.^[39]

Politopul complex regulat ₃{4}₃, sau , în ${\displaystyle \mathbb {C} ^{2}}$ are o reprezentare reală un 24-celule în spațiul cvadridimensional. ₃{4}₃ are 24 de vârfuri și 24 de 3-laturi. Simetria sa este ₃[4]₃, ordinul 72.

Figuri asociate în proiecție ortogonală

Nume	{3,4,3},	4{3}4,	3{4}3,
Simetrie	[3,4,3], , ordin 1152	4[3]4, , ordin 96	3[4]3, , ordin 72
Vârfuri	24	24	24
Laturi	96 2-laturi	24 4-laturi	24 3-laturi
Imagine	24-celule în planul Coxeter F4, cu 24 de vârfuri în două inele de 12 și 96 de laturi	4{3}4, are 24 de vârfuri și 32 de 4-laturi în pătrate, câte 8 colorate aici cu roșu, verde, albastru și galben.	3{4}3 sau are 24 de vârfuri și 24 de 3-laturi, câte 8 colorate aici roșu, verde și albastru, cu laturile albastre colorate complet.

4-politopuri asociate

Mai multe 4-politopuri uniforme pot fi obținute din 24-celule prin trunchiere:

• trunchierea la 1/3 din lungimea laturilor produce 24-celule trunchiat;
• trunchierea la 1/2 din lungimea laturilor produce 24-celule rectificat;
• trunchierea la jumătate a dualului 24-celule produce 24-cell bitrunchiat, care este izotop.

Pe cele 96 de laturi ale 24-celulelor se pot amplasa la secțiunea de aur cele 96 de vârfuri ale unui 24-celule snub. O modificare analogă a unui octaedru produce un icosaedru, sau „octaedru snub”.

24-celule este unicul politop euclidian regulat convex autodual, care nu este nici un poligon, nici un simplex. Relaxarea condiției de convexitate permite alte două figuri: marele 120-celule și marele 120-celule stelat. Împreună cu el însuși poate forma un compus politopic: compus din două 24-celule (v. mai sus).

Politopuri uniforme asociate

4-politopuri uniforme cu simetrie D4
{3,31,1} h{4,3,3}	2r{3,31,1} h3{4,3,3}	t{3,31,1} h2{4,3,3}	2t{3,31,1} h2,3{4,3,3}	r{3,31,1} {31,1,1}={3,4,3}	rr{3,31,1} r{31,1,1}=r{3,4,3}	tr{3,31,1} t{31,1,1}=t{3,4,3}	sr{3,31,1} s{31,1,1}=s{3,4,3}

Familia politopurilor 24-celule
Nume	24-celule	24-celule trunchiat	24-celule snub	24-celule rectificat	24-celule cantelat	24-celule bitrunchiat	24-celule cantitrunchiat	24-celule runcinat	24-celule runcitrunchiat	24-celule omnitrunchiat
Simbol Schläfli	{3,4,3}	t0,1{3,4,3} t{3,4,3}	s{3,4,3}	t1{3,4,3} r{3,4,3}	t0,2{3,4,3} rr{3,4,3}	t1,2{3,4,3} 2t{3,4,3}	t0,1,2{3,4,3} tr{3,4,3}	t0,3{3,4,3}	t0,1,3{3,4,3}	t0,1,2,3{3,4,3}
Diagramă Coxeter
Diagramă Schlegel
F4
B4
B3(a)
B3(b)
B2

24-celule poate fi obținut și ca 16-celule rectificat:

Politopuri cu simetrie B4
Nume	Tesseract	Tesseract rectificat	Tesseract trunchiat	Tesseract cantelat	Tesseract runcinat	Tesseract bitrunchiat	Tesseract cantitrunchiat	Tesseract runcitrunchiat	Tesseract omnitrunchiat
Diagramă Coxeter		=				=
Simbol Schläfli	{4,3,3}	t1{4,3,3} r{4,3,3}	t0,1{4,3,3} t{4,3,3}	t0,2{4,3,3} rr{4,3,3}	t0,3{4,3,3}	t1,2{4,3,3} 2t{4,3,3}	t0,1,2{4,3,3} tr{4,3,3}	t0,1,3{4,3,3}	t0,1,2,3{4,3,3}
Diagramă Schlegel
B4
Nume	16-celule	16-celule rectificat	16-celule trunchiat	16-celule cantelat	16-celule runcinat	16-celule bitrunchiat	16-celule cantitrunchiat	16-celule runcitrunchiat	16-celule omnitrunchiat
Diagramă Coxeter	=	=	=	=		=	=
Simbol Schläfli	{3,3,4}	t1{3,3,4} r{3,3,4}	t0,1{3,3,4} t{3,3,4}	t0,2{3,3,4} rr{3,3,4}	t0,3{3,3,4}	t1,2{3,3,4} 2t{3,3,4}	t0,1,2{3,3,4} tr{3,3,4}	t0,1,3{3,3,4}	t0,1,2,3{3,3,4}
Diagramă Schlegel
B4

Teselări simetrice:

Politopuri {3,p,3}
Spațiu	S3		H3
Formă	Finit		Compact	Paracompact	Necompact
{3,p,3}	{3,3,3}	{3,4,3}	{3,5,3}	{3,6,3}	{3,7,3}	{3,8,3}	... {3,∞,3}
Imagine
Celule	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	[[{3,∞}
Figura vârfului	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Note explicative

1. „24-celule” este o prescurtare a expresiei din limba română „un politop cvadridimensional format din 24 de celule”, plural „două sau mai multe politopuri cvadridimesnsionale formate din câte 24 de celule”, expresii care se acordă corespunzător, deci se vorbește despre „un/acel 24-celule”, nu „o/acea 24-celule”, respectiv „unele/acele 24-celule”', nu „unii/acei 24-celule”. La fel la celelalte politopuri ale căror nume este de forma „n-celule”.
2. 24-celule este unul dintre cele trei politopuri euclidiene regulate care nu sunt nici poligon, nici simplex. Celelalte două sunt și ele 4-politopuri, dar nu convexe: marele 120-celule stelat și marele 120-celule.
3. Politopurile regulate convexe din primele patru dimensiuni cu un 5 în simbolul lor Schlӓfli sunt pentagonul {5}, dodecaedrul {5,3}, 600-celule {3,3,5} și 120-celule {5,3,3}. Cu alte cuvinte, 24-celule posedă toate caracteristicile triunghiulare și pătrate care există în patru dimensiuni, cu excepția 5-celule regulat, dar niciuna dintre caracteristicile pentagonale. (5-celule este, de asemenea, pentagonală în sensul că poligonul său Petrie este pentagonul.)
4. Doar câteva politopuri uniforme au această proprietate: în 4 dimensiuni 24-celule și tesseractul, în 3 dimensiuni cuboctaedrul, iar în 2 dimensiuni hexagonul. (Cuboctaedrul este secțiunea transversală ecuatorială a 24-celule, iar hexagonul este secțiunea transversală ecuatorială a cuboctaedrului.) Politopurile echilaterale radial sunt cele care pot fi construite din triunghiuri echilaterale care se întâlnesc în centrul politopului, fiecare contribuind cu două raze și o latură.
5. laturile pătratelor sunt aliniate cu direcțiile axelor de coordonate. De exemplu:

   (  0,–1,  1,  0)   (  0,  1,  1,  0)

   (  0,–1,–1,  0)   (  0,  1,–1,  0)
   

   este pătratul din planul xy. Laturile pătratelor nu sunt laturi ale 24-celulei, ele sunt coarde între două vârfuri aflate la 90° distanță unul de altul, astfel că pătratele sunt doar configurații invizibile între 4 din vârfurile 24-celulei.
6. În 4 dimensiuni pot fi reciproc ortogonale până la 6 plane. Spațiul tridimensional are doar 3 axe perpendiculare și 3 plane perpendiculare într-un singur punct. În spațiul cvadridimensional există 4 axe perpendiculare și 6 plane perpendiculare într-un punct (din același motiv pentru care tetraedrul are 6 muchii, nu 4): există 6 combinări de câte 2 dimensiuni din cele 4. Trei astfel de perechi (perechi de axe) se întâlnesc în fiecare vârf al unui 24-celule (din același motiv pentru care trei laturi ale tetraedrului se întâlnesc la fiecare vârf al tetraedrului). Fiecare din cele 6 plane este ortogonal pe fiecare dintre celelalte, singurul cu care nu are în comun o latură (din același motiv pentru care fiecare latură a tetraedrului este ortogonală doar pe una dintre celelalte laturi: singura cu care nu are în comun niciun punct). Două plane complet ortogonale sunt perpendiculare și opuse unul altuia, la fel cum două muchii ale tetraedrului sunt perpendiculare și opuse.
7. Despre două plane plate A și B ale unui spațiu euclidian cvadridimensional se spune că sunt complet ortogonale dacă și numai dacă fiecare dreaptă din A este ortogonală cu fiecare linie din B. În acest caz, planele A și B se intersectează într-un singur punct O, astfel încât dacă o dreaptă din A se intersectează cu o dreaptă din B, acestea se intersectează în O.^{[lower-alpha 6]}
8. Două plane în spațiul cvadridimensional pot avea patru poziții reciproce posibile: (1) pot coincide (să fie exact același plan); (2) pot fi paralele (singurul mod în care reușesc să nu se intersecteze deloc); (3) se pot intersecta pe o singură dreaptă, la fel ca două plane neparalele în spațiul tridimensional; sau (4) se pot intersecta într-un singur punct dacă sunt complet ortogonale^{[lower-alpha 7]}.
9. Laturile pătratelor ortogonale ecuatoriale nu sunt aliniate cu planele sistemului de coordonate. Șase dintre pătrate se află în cele 6 plane ortogonale ale sistemului de coordonate, dar muchiile lor sunt coarde (√2) ale pătratelor unitare ale rețelei de coordonate. De exemplu:

   (  0,  0,  1,  0)

   (  0,–1,  0,  0)   (  0,  1,  0,  0)

   (  0,  0,–1,  0)
   

   este pătratul din planul xy. Se observă că cele 8 coordonate întregi sunt ale vârfurilor celor 6 pătrate ortogonale.
10. Hexagoanele sunt înclinate în raport cu planele ortogonale ale sistemului de coordonate. Fiecare plan conține doar una din cele 4 axe ale sistemului de coordonate. Hexagonul este format din 3 perechi de vârfuri opuse (trei diametre ale 24 de celule): o pereche opusă de vârfuri cu coordonate întregi (una dintre cele patru axe de coordonate) și două perechi de vârfuri opuse cu coordonate jumătate de întreg (nu pe axele de coordonate). De exemplu:

    (  0,  0,  1,  0)

    (  1/2,–1/2,  1/2,–1/2)   (  1/2,  1/2,  1/2,  1/2)

    (–1/2,–1/2,–1/2,–1/2)   (–1/2,  1/2,–1/2,  1/2)

    (  0,  0,–1,  0)
    

    este un hexagon pe axa „y”. Spre deosebire de pătratele √2, hexagoanele sunt de fapt formate din laturi ale 24-celulei, deci sunt caracteristici vizibile ale 24-celulei.
11. Câte opt laturi √1 converg în spațiul tridimensional al vârfurilor figurilor cubice ale vârfurilor 24-celulei^{[lower-alpha 21]} și se întâlnesc în centrul vârfului, unde formează 4 drepte care se intersectează acolo. Cele 8 vârfuri ale cubului sunt cele opt cele mai apropiate vârfuri ale 24-celulei. Dreptele sunt geodezice: două segmente de lungime √1 ale unei linii aparent drepte (în spațiul tridimensional al frontierei curbate a 24-celulei) care sunt îndoite în cea de-a 4-a dimensiune într-un cerc mare cu hexagon (în 4-spațiu). Văzut din interiorul acestui 3-spațiu curbat, coturile din hexagoane sunt invizibile. Din exterior (dacă s-ar putea vizualiza 24-celule în 4-spațiu), liniile drepte ar fi văzute îndoindu-se în a 4-a dimensiune în centrele cuburilor, deoarece centrul 24-celulei este deplasat în a 4-a dimensiune, în afara hiperplanului definit de vârfurile cubului. Astfel, cubul vârfului este de fapt o piramidă cubică. Spre deosebire de un cub, pare a fi echilateral radial (ca și tesseractul și 24-celule însuși): raza sa este egală cu lungimea laturii.^{[lower-alpha 22]}
12. Nu este dificil de vizualizat chiar și în 3 dimensiuni patru plane hexagonale care se intersectează la 60° unul față de celălalt. patru dintre cele 16 plane centrale hexagonale (care se află în același hiperplan tridimensional) se intersectează în fiecare dintre vârfurile 24-celule exact așa cum o fac în centrul unui cuboctaedru. Dar laturile din jurul vârfului nu se întâlnesc așa cum se întâlnesc razele în centrul unui cuboctaedru; 24-celule are 8 laturi în jurul fiecărui vârf, nu 12, deci figura sa a vârfului este cubul, nu cuboctaedrul. Cele 8 laturi se întâlnesc exact așa cum se întâlnesc 8 laturi în apexul unei piramide cubice canonice.^{[lower-alpha 11]}
13. 24-celule are 4 seturi de 4 cercuri mari paralele Clifford^{[lower-alpha 18]} care nu se intersectează, fiecare trecând prin 6 vârfuri (un hexagon mare), cu un singur hexagon mare în fiecare set care trece prin fiecare vârf și cele 4 hexagoane din fiecare set atingând toate cele 24 de vârfuri. Astfel, fiecare mulțime constituie un fibrat Hopf discret de cercuri mari interconectate. Fiecare dintre cele 4 fibrate poate fi, de asemenea, împărțit (în trei moduri diferite) în 2 subseturi disjuncte a câte 12 vârfuri, fiecare formând un dodecagon strâmb care se află pe o geodezică izoclinică elicoidală sau izoclină care este calea urmată de acele 12 vârfuri într-o anumită rotație izoclinică.^{[lower-alpha 29]} O spirală dodecagonală spiralează într-o rotație izoclinică la dreapta, iar cealaltă spirală de dodecagon spiralează într-o rotație izoclinică la stângă. Deși aceste 2 elice dodecagonale disjuncte au o chiralitate opusă, ele sunt jumătăți paralele Clifford ale aceluiași fibrat. Fiecare dodecagon spirală include jumătate din vârfurile 24-celule: jumătate din vârfurile fiecăreia dintre cele 4 fibrate hexagonale paralele Clifford (3 vârfuri ale unui √3 triunghi înscris în fiecare hexagon) și jumătate din vârfurile fiecăruia dintre cele 12 diametre √4 (1 capăt al fiecărui diametru).
14. Aceste triunghiuri se află în aceleași plane ortogonale care conțin hexagoanele;^{[lower-alpha 10]} două triunghiuri cu lungimea laturii √3 sunt înscrise în fiecare hexagon. De exemplu, în coordonatele cu rază unitară:

    (  0,  0,  1,  0)

    (  1/2,–1/2,  1/2,–1/2)   (  1/2,  1/2,  1/2,  1/2)

    (–1/2,–1/2,–1/2,–1/2)   (–1/2,  1/2,–1/2,  1/2)

    (  0,  0,–1,  0)
    

    sunt două triunghiuri centrale opuse pe axa y, cu fiecare triunghi format de vârfuri alternate. Spre deosebire de hexagoane, triunghiurile √3 nu sunt formate din laturi reale ale 24-celulei, deci sunt caracteristici invizibile ale 24-celulei, cum ar fi pătratele √2.
15. Acestea nu sunt planele ortogonale ale sistemului de coordonate; laturile de lungime √3 ale acestor triunghiuri sunt diagonalele celulelor cubice din 24-celule, dar acele celule cubice (tesseracte) nu sunt aliniate cu rețeaua coordonatelor.
16. Caracteristicile interioare nu sunt considerate elemente ale politopului. De exemplu, centrul unei celule de 24 de celule este o caracteristică demnă de remarcat (la fel ca și razele sale lungi), dar aceste caracteristici interioare nu sunt luate în considerare ca elemente în matricea sa de configurare, care numără doar caracteristicile elementare (care nu sunt în interiorul niciunei alte caracteristici, inclusiv politopului însuși). Caracteristicile interioare nu sunt redate în majoritatea diagramelor și ilustrațiilor din acest articol (în mod normal sunt invizibile). În ilustrațiile care prezintă caracteristici interioare, desenăm întotdeauna marginile interioare ca linii întrerupte, pentru a le distinge de marginile elementare.
17. Vârful central este un vârf canonic, deoarece este echidistant de celelalte vârfuri din a 4-a dimensiune, la fel cum vârful (apexul) unei piramide canonice este echidistant față de celelalte vârfuri ale sale.
18. Paralelele Clifford sunt linii curbe care nu se intersectează, sunt paralele în sensul că distanța perpendiculară (cea mai mică) dintre ele este aceeași în fiecare punct.^[9] În spațiul tridimensional euclidian obișnuit un exemplu de paralelism Clifford este o elice dublă. În spațiul euclidian cvadridimensional, paralelele Clifford apar ca cercuri mari geodezice pe 3-sferă.^[10] În timp ce în spațiul tridimensional, oricare două cercuri mari geodezice de pe o 2-sferă se vor intersecta întotdeauna în două puncte antipodale, în spațiul cvadridimensional nu toate cercurile mari se intersectează: pe o 3-sferă pot fi găsite diferite seturi de cercuri mari geodezice paralele Clifford neintersectate. Poate cel mai simplu exemplu este că șase cercuri mari reciproc ortogonale pot fi desenate pe o 3-sferă ca trei perechi de cercuri mari complet ortogonale.^{[lower-alpha 6]} Fiecare pereche complet ortogonală este paralelă Clifford. Cele două cercuri nu se pot intersecta deloc, deoarece se află în plane care se intersectează doar într-un singur punct: centrul 3-sferei.^{[lower-alpha 25]} Deoarece sunt perpendiculare și au un centru comun, cele două cercuri nu sunt în mod evident paralele și separate în modul obișnuit al cercurilor paralele din spațiul tridimensional. Ele sunt conectate ca niște zale adiacente dintr-un lanț, fiecare trecând prin altul (fără să se intersecteze în niciun punct), formând o verigă Hopf.
19. Un cerc mare geodezic se află într-un plan bidimensional care trece prin centrul politopului. În spațiul cvadridimensional acest plan central nu divide politopul în două părți egale, așa cum ar face în spațiul tridimensional, la fel cum un diametru divide un cerc, dar nu și o sferă. O altă diferență este că în cvadridimensional nu toate perechile de cercuri mari se intersectează în două puncte, așa cum se întâmplă în tridimensional; unele perechi o fac, dar unele perechi de cercuri mari sunt paralele Clifford, care nu se intersectează.^{[lower-alpha 18]}
20. Dacă distanța euclidiană dintre oricare două vârfuri este √1, distanța lor geodezică este 1; pot fi două vârfuri adiacente (în 3-spațiul curbat al frontierei) sau un vârf și centrul (în 4-spațiu). Dacă distanța lor euclidiană este √2, distanța lor geodezică este 2 (fie prin 3-spații sau 4-spații, deoarece calea de-a lungul laturilor este aceeași linie dreaptă cu o îndoire de 90° pe drumul prin centru). Dacă distanța lor euclidiană este √3, distanța lor geodezică este tot 2 (fie pe un cerc mare hexagonal îndoit la 60° la trecerea prin centru, fie ca o linie dreaptă îndoită cu 60° la trecerea prin centru). În cele din urmă, dacă distanța lor euclidiană este √4, distanța lor geodezică este totuși 2 în 4-spațiu (direct prin centru), dar ajunge la 3 în 3-spațiu (făcând jumătate de drum pe un cerc mare hexagonal)
21. Figura vârfului este fațeta care se realizează prin trunchierea unui vârf; canonic, la mijlocul laturilor incidente la vârf. Dar se pot face figuri similare de vârfuri de raze diferite prin trunchierea în orice punct de-a lungul acelor laturi, până la trunchierea la vârfurile adiacente inclusiv aceste vârfuri, pentru a face o figură a vârfului de dimensiune completă. Stillwell definește figura vârfului ca „anvelopa convexă al vârfurilor învecinate unui vârf dat”.^[8]
22. Piramida cubică a vârfului nu este de fapt echilaterală radial,^{[lower-alpha 4]} deoarece laturile care radiază din apexul său nu sunt de fapt razele sale: apexul piramidei cubice nu este de fapt centrul său, ci doar unul dintre vârfurile sale.
23. Șase coarde √2 converg în spațiul tridimensional al vârfurilor figurilor cubice ale vârfurilor 24-celulei și se întâlnesc în centrul vârfului, unde formează 3 drepte care se intersectează acolo perpendicular. Cele 8 vârfuri ale cubului sunt cele opt cele mai apropiate vârfuri ale 24-celulei, iar opt laturi √1 converg acolo, dar momentan vor fi ignorate pentru a simplifica vizualizarea. Fiecare dintre cele șase coarde √2 pleacă din centrul acestui cub (vârful 4-dimensional) și trece printr-un centru al unei feței până la centrul cubului adiacent feței, care este un alt vârf al 24-celulei: nu un cel mai apropiat vârf (cele din colțurile cubului), dar unul situat la 90° distanță într-un al doilea strat concentric de șase vârfuri la distanța de √2 care înconjoară primul strat de opt vârfuri de la distanța de √1. Centrul feței prin care trece coarda √2 este punctul median al coardei √2, deci se află în interiorul 24-celulei.
24. Un 24-celule poate fi divizat în două părți egale prin 6 vârfuri (în orice plan al unui cerc mare cu hexagon) sau prin 4 vârfuri (în orice plan al unui cerc mare cu pătrat). Se poate vedea acest lucru la cuboctaedru (hiperplanul central al 24-celulei), unde există patru cercuri mari cu hexagoane (de-a lungul laturilor) și șase cercuri mari cu pătrate (peste fețele pătrate în diagonală).
25. Fiecare plan pătratic este izoclinic (paralel Clifford) cu alte cinci plane pătratice, dar complet ortogonal^{[lower-alpha 7]} cu doar unul din ele.^{[lower-alpha 32]} Fiecare pereche de plane complet ortogonale are cercuri mari paralele Clifford, dar nu toate cercurile mari paralele Clifford sunt ortogonale (de exemplu, niciuna dintre geodezicele hexagonale din 24-celule nu sunt reciproc ortogonale).
26. Opt coarde √3 converg din colțurile figurii vârfului cubic al 24-celulei și se întâlnesc în centrul acestuia (vârful 24-celulei), unde formează 4 drepte care se intersectează acolo. Fiecare dintre cele opt √3 coarde merge din centrul acestui cub până la centrul unui cub adiacent diagonal (la un vârf), care este un alt vârf al 24-celulei: unul situat la 120° distanță într-un al treilea strat concentric de opt vârfuri la distanța √3, care înconjoară al doilea strat de șase vârfuri, de la distanța √2.
27. Suma 1・96 + 2・72 + 3・96 + 4・12 este 576.
28. Suma pătratelor lungimilor tuturor acestor coarde distincte ale oricărui n-politop convex regulat de rază unitate este pătratul numărului de vârfuri.^[11]
29. Într-o rotație izoclinică, cunoscută și ca deplasare Clifford, un punct traversează în diagonală^{[lower-alpha 57]} dreapta unei singure geodezice izoclinice, ajungând direct la destinație, în locul liniei îndoite a două geodezice simple succesive. O geodezică este cea mai scurtă cale printr-un spațiu (în mod intuitiv, o sfoară întinsă între două puncte). Geodezice simple sunt cercuri mari situate într-un plan central (singurul tip de geodezice care apar în spațiul tridimensional pe o sferă bidimensională). Geodezicele izoclinice sunt diferite: ele nu se află într-un singur plan; sunt mai degrabă un fel de spirale tridimensionale decât cercuri bidimensionale.^{[lower-alpha 53]} Dar nici ele nu sunt ca filetele, pentru că în cele din urmă formează o buclă închisă ca orice cerc (după două revoluții), ca orice cerc.^{[lower-alpha 59]} Geodezice izoclinice sau „izoclinele” sunt cercuri mari tridimensionale și sunt la fel de „cercuri” ca și cercurile bidimensionale: de fapt, de două ori mai circulare, deoarece se curbează într-un cerc în două direcții complet ortogonale simultan. Ele apar întotdeauna în perechi chirale și formează o pereche de cercuri Villarceau pe un tor Clifford, căile rotației izoclinice pe stânga și pe dreapta. Ele sunt elice îndoite într-un buclă Möbius în a patra dimensiune, urmând un traseu dublu de înconjurare în diagonală în jurul 3-sferei prin vârfurile neadiacente ale unui poligon stelat strâmb al 4-politopului.
30. Fiecare pereche de laturi paralele √1 formează cu o pereche de coarde paralele √3 unul din cele 48 de dreptunghiuri (înscrise în cele 16 hexagoane centrale), iar fiecare pereche de coarde paralele √2 formează împreună cu altă pereche de coarde paralele √2 unul din cele 18 pătrate centrale.
31. O modalitate de a vizualiza hiperplanul n-dimensional este ca n-spațiile care pot fi definite prin n + 1 puncte. Un punct este 0-spațiul care este definit de 1 punct. O linie este 1-spațiul care este definit de 2 puncte care nu sunt coincidente. Un plan este 2-spațiul care este definit de 3 puncte care nu sunt coliniare (orice triunghi). În 4-spațiu, un hiperplan tridimensional este 3-spațiul care este definit de 4 puncte care nu sunt coplanare (orice tetraedru). În 5-spațiu, un hiperplan cvadridimensional este 4-spațiul care este definit de 5 puncte care nu sunt cocelulare (orice 5-celule). Aceste simplexuri înpart hiperplanul în două părți (în interiorul și în exteriorul figurii), dar în plus, împart universul (spațiul închizător) în două părți („deasupra” și „dedesubtul” hiperplanului). Cele n puncte mărginesc un simplex finit (față de exterior) și definesc un hiperplan infinit (față de interior).^[26] Aceste două diviziuni sunt ortogonale, deci simplexul definitoriu împarte spațiul în șase regiuni: în interiorul simplexului și în hiperplan, în interiorul simplexului dar deasupra sau dedesubtul hiperplanului, în afara simplexului dar în hiperplan și în afara simplexului dar deasupra sau dedesubtul hiperplanului.
32. Într-un 16-celule cele 6 pătrate mari ortogonale formează 3 perechi de cercuri mari complet ortogonale; fiecare pereche este paralelă Clifford. În 24-celule, cele 3 16-celule se află rotite izoclinic la 60° una față de alta, prin urmare vârfurile lor sunt toate la 60° pe un cerc mare hexagonal. Împerecherea vârfurilor lor, care sunt la 90° unul față de altul, indică cercul mare corespondent, paralel Clifford. Fiecare dintre cele 18 cercuri mari pătratice sunt paralele Clifford nu numai cu un alt cerc mare pătratic din același 16-celule (cel complet ortogonal), ci și cu două cercuri mari pătratice (care sunt complet ortogonale între ele) din fiecare dintre celelalte două 16-celule. (Cercurile mari complet ortogonale sunt paralele Clifford, dar nu toate paralelele Clifford sunt ortogonale.^{[lower-alpha 25]}) O rotație izoclinică de 60° a unei 24-celule în planele hexagonale invariante duce fiecare cerc mare pătratic la un cerc mare pătratic paralel Clifford (dar nu ortogonal) într-o altă 16-celule.
33. Pentru a fixa pozițiile relative a două plane în spațiulcvadridimensional sunt necesare două unghiuri.^[12] Deoarece toate planele din același hiperplan^{[lower-alpha 31]} unul dintre unghiuri este de 0°, în spațiul tridimensional mai este necesar un singur unghi. Două hexagoane mari din hiperplane diferite sunt la 90° unul de altul în ambele unghiuri. Două pătrate mari din hiperplane diferite sunt la 90° unul de altul în ambele unghiuri (sunt complet ortogonale).^{[lower-alpha 7]}sau la 60° unul de altul în ambele unghiuri.^{[lower-alpha 32]} Planele care sunt separate de două unghiuri egale se numesc izoclinice. Planele care sunt izoclinice au cercuri mari paralele Clifford.^{[lower-alpha 18]} Un pătrat mare și un hexagon mare aflate în hiperplane diferite nu sunt nici izoclinice, nici paralele Clifford; sunt separate printr-un unghi de 90° și un unghi de 60°.
34. Fiecare pereche de poligoane paralele Clifford se află în două hiperplane (cuboctaedre) diferite. Cele 4 hexagoane paralele Clifford se află în 4 cuboctaedre diferite.
35. În cele 24 de celule, fiecare plan pătrat mare este complet ortogonal^{[lower-alpha 7]} cu un alt plan pătrat mare, iar fiecare plan hexagonal mare este complet ortogonal cu un plan care intersectează doar două vârfuri: un plan mare digonal.
36. 600-celule este mai mare decât 24-celule și conține pe 24-celule drept caracteristică interioară.^[13] 5-celule regulat nu se găsește în interiorul niciunui 4-politop regulat convex, cu excepția a 120-celule,^[14] deși fiecare 4-politop poate fi descompus radial în 5-celule neregulate.
37. Fiecare plan al unei fețe a celulei se intersectează cu celelalte plane ale feței de acest tip care nu este complet ortogonal sau paralel cu o coardă a vârfului său caracteristic. Planele fețelor adiacente ale celulelor cu fețe ortogonale (cum ar fi cuburile) se intersectează pe o latură deoarece nu sunt complet ortogonale.^{[lower-alpha 8]} Deși unghiul lor diedru este de 90° în 3-spațiu, ele se află în același hiperplan ^{[lower-alpha 31]} (în a patra dimensiune sunt mai degrabă coincidente decât perpendiculare); astfel se intersectează într-o dreaptă, așa cum fac planele neparalele în orice 3-spațiu.
38. Singurele plane prin exact 6 vârfuri ale 24-celulei (fără a lua în considerare vârful central) sunt cele ale celor 16 cercuri mari cu hexagoane. Nu există plane prin exact 5 vârfuri. Există mai multe tipuri de plane prin exact 4 vârfuri: cele 18 √2 ale cercurilor mari cu pătrate, cele ale celor 72 √1 de fețe pătrate (ale tesseractelor) și 144 √1 pe √2 dreptunghiuri. Planele prin exact 3 vârfuri sunt cele ale celor 96 de fețe triunghiulare echilaterale √2 ale 16-celulelor și ale color 96 de fețe triunghiulare echilaterale √1 ale 24-celulei. Există un număr infinit de plane centrale prin exact două vârfuri (cercuri mari digonale); 16 se disting deoarece fiecare este complet ortogonal^{[lower-alpha 7]} cu unul dintre cele 16 cercuri mari hexagonale.
39. Figurile cubice ale vârfurilor 24-celulei au fost trunchiate la figuri ale vârfului tetraedrice (v. desenele lui Kepler). Cubul vârfului a dispărut și acum există doar 4 colțuri ale figurii vârfului care înainte avea 8. Patru laturi de teseract converg de la vârfurile tetraedrului și se întâlnesc în centrul acestuia, unde nu se intersectează, deoarece tetraedrul nu are vârfuri opuse.
40. Nucleul comun este cel din sfera înscrisă a 24-celulei, cu raza 1/2. Rectificarea oricăreia dintre cele trei 16-celule relevă acest 24-celule mai mic, care are un 4-conținut de doar 1/8 (1/16 din cel al 24-celulei). Vârfurile sale se află în centrele celulelor octaedrice ale 24-celulei inițiale, care sunt și centrele fețelor pătrate ale tesseractelor și sunt și centrele laturilor 16-celulelor.
41. Figura cubică a vârfului a 24-celulei a fost trunchiată la o figură a vârfului octaedrică. Cubul vârfului a dispărut și acum există doar 6 colțuri ale figurii vârfului care înainte avea 8. Cele 6 coarde √2 care anterior convergeau din centrele feței cubului converg acum din vârfurile octaedrului; dar, la fel ca înainte, se întâlnesc în centru, unde 3 drepte se intersectează perpendicular. Vârfurile octaedrului sunt situate la 90° în afara cubului dispărut, în noile vârfuri cele mai apropiate; înainte de tăiere, acestea erau vârfuri ale 24-celulei din al doilea strat al vârfurilor înconjurătoare.
42. Politopurile sunt complet disjuncte dacă toate seturile lor de elemente sunt disjuncte: nu au în comun vârfuri, muchii, fețe sau celule. Ele se pot suprapune în continuare în spațiu, având în comun 4-conținut, volum, arie sau laturi.
43. Conținutul în 4 dimensiuni al tesseractului a cărui lungime a laturii este √1 este de 1 (prin definiție). Conținutul 24-celulei cu lungimea laturii √1 este de 2, deci jumătate din conținutul său se află în interiorul tesseractelor, iar jumătate se află între anvelopele lor. Fiecare 16-celule (având lungimea laturii √2) cuprinde un conținut de 2/3, lăsând 1/3 între avelopele tesseractelor și cele ale lor.
44. Între anvelopa 24-celulei și anvelopele a 8-celule sunt cele 8 piramide cubice ale construcției lui Gosset. Între anvelopele 8-celulelor și anvelopele 16-celulelor sunt 16 5-celule, cu vârfurile lor umplând colțurile tesseractului.
45. Dintre cele trei diametre lungi perpendiculare √2 ale celulei octaedrice^[23] două dintre ele sunt diagonalele feței pătrate dintre două cuburi; fiecare este o coardă √2 care conectează două vârfuri ale acestor cuburi ale 8-celulei pe o față pătrată, conectează două vârfuri opuse a două tetraedre ale 16-celulelor (înscrise în cuburi) și conectează două vârfuri opuse ale unui octaedru al 24-celulei (diagonal pe două dintre cele trei secțiuni centrale pătrate ortogonale). Al treilea diametru lung perpendicular al octaedrului face exact același lucru (prin simetrie); deci și el conectează două vârfuri ale unei perechi de cuburi pe fața lor pătrată comună (dar o pereche diferită de cuburi, din alt tesseract din acel 24-celule).
46. Deoarece există trei tesseracte suprapuse înscrise în 24-celule, fiecare celulă octaedrică se află pe o celulă cubică dintr-un tesseract (în piramida cubică bazată pe cub, dar nu în volumul cubului) și în două celule cubice, fiecare dintre ele în altul din cele două tesseracte (celule cubice care au în comun volumul lor).^{[lower-alpha 45]}
47. Acest lucru ar putea părea la început imposibil din punct de vedere al unghiurilor și, într-adevăr, ar fi într-un spațiu tridimensional. Dacă două cuburi stau unul lângă altul într-un spațiu obișnuit tridimensional (de exemplu pe suprafața unei mese într-o cameră obișnuită tridimensională), un octaedru se va potrivi în interiorul lor astfel încât patru din cele șase vârfuri ale sale să fie în cele patru colțuri ale feței pătrate dintre cele două cuburi; dar celelalte două vârfuri octaedrice nu vor fi în alte vârfuri ale cuburilor (vor fi în interiorul volumelor celor două cuburi). În patru dimensiuni, acest lucru nu este mai puțin adevărat! Celelalte două vârfuri ale octaedrului nu se află în vreun vârf al unui cub adiacent unei fețe în același tesseract. Însă în 24-celule nu există doar un singur tesseract (din 8 cuburi) înscris, există trei tesseracte suprapuse (din câte 8 cuburi fiecare). Celelalte două vârfuri octaedrice se află în vârfurile altui cub: dar un cub din alt tesseract, suprapus.^{[lower-alpha 46]}
48. Este important să se vizualizeze razele doar ca caracteristici interioare invizibile ale 24-celulei (linii punctate), deoarece acestea nu sunt laturi ale fagurelui. În mod similar, centrul 24-celulei este gol (nu un vârf al fagurelui).
49. Spre deosebire de 24-celule și tesseract, 16-celule nu este radial echilateral; prin urmare, 16-celule de două mărimi diferite (lungimea unității muchiei versus raza unității) apar în fagurele cu lungimea laturii o unitate. Cei 24 de 16-celule care se întâlnesc în centrul fiecărui 24-celule au lungimea laturii o unitate și raza √2/2. Cei trei 16-celule înscriși în fiecare 24-celule au lungimea laturii √2 și raza o unitate.
50. Rotațiile în patru dimensiuni pot apărea în jurul unui plan, ca atunci când celulele adiacente sunt pliate în jurul planului lor de intersectare (prin analogie cu felul în care fețele adiacente sunt pliate în jurul liniei lor de intersectare).^{[lower-alpha 51]} Dar în patru dimensiuni există încă un alt mod în care pot apărea rotații, numit rotație dublă. Rotațiile duble sunt un fenomen emergent în a patra dimensiune și nu au analogie în trei dimensiuni: plierea fețelor pătrate și plierea celulelor cubice sunt ambele exemple de rotații simple, singurul tip care are loc în mai puțin de patru dimensiuni. În rotațiile tridimensionale, punctele dintr-o linie rămân fixe în timpul rotației, în timp ce orice alt punct se mișcă. În rotațiile simple 4-dimensionale, punctele dintr-un plan rămân fixe în timpul rotației, în timp ce orice alt punct se mișcă. În rotațiile duble 4-dimensionale un punct rămâne fix în timpul rotației și orice alt punct se mișcă (ca într-o rotație bidimensională!).^{[lower-alpha 52]}
51. Rotațiile tridimensionale apar în jurul unei axe. Rotațiile în spațiul cvadridimensional pot apărea în jurul unui plan. Deci, în trei dimensiuni se pot plia plane în jurul unei drepte comune (ca atunci când se pliază o desfășurată de 6 pătrate din plan într-un cub), iar în patru dimensiuni se pot plia celule în jurul unui plan comun (ca atunci când se pliază desfășurata de 8 cuburi într-un tesseract). Plierea în jurul unei fețe pătrate înseamnă doar plierea simultană în jurul a două din laturile sale ortogonale; nu există suficient spațiu în trei dimensiuni pentru a face acest lucru, la fel cum nu există suficient spațiu în două dimensiuni pentru a se plia în jurul unei linii (doar suficient pentru a se plia în jurul unui punct).
52. Există (cel puțin) două tipuri de analogii dimensionale corecte: tipul obișnuit între dimensiunea n și dimensiunea n+1, și tipul mult mai rar și mai puțin evident între dimensiunea n și dimensiunea n+2. Un exemplu al acestuia din urmă este că rotațiile în 4-spații pot avea loc în jurul unui singur punct, la fel cu rotațiile în 2-spații. Altul este regula n-sferei că aria suprafeței sferei din dimensiunea n+2 este exact de ${\displaystyle 2\pi r}$ ori volumul închis de sfera din dimensiunea n, cele mai cunoscute exemple fiind că circumferința unui cerc este de ${\displaystyle 2\pi r}$ ori 1 și suprafața sferei obișnuite este de ${\displaystyle 2\pi r}$ ori 2r . Coxeter citează^[31] aceasta ca un exemplu în care analogia dimensională pare a eșua ca metodă, dar este de fapt eșecul nostru de a recunoaște dacă o analogie unidimensională sau bidimensională este metoda potrivită.
53. Într-o rotație dublă se poate spune că fiecare vârf se mișcă simultan de-a lungul a două cercuri mari complet ortogonale, dar nu rămâne în planul central al vreuneia dintre acele cercuri mari originale; mai degrabă, se mișcă de-a lungul unei geodezice elicoidale care traversează în diagonală între cercurile mari. Rotațiile duble au două forme chirale: rotații la stânga și la dreapta. Într-o rotație dublă, fiecare vârf se mișcă în spirală de-a lungul a două plane mari complet ortogonale. Cele două plane de rotație complet ortogonale se spune că sunt invariante deoarece punctele din fiecare stau în plan pe măsură ce planul se mișcă, înclinând lateral cu același unghi cu care se rotește celălalt plan.
54. Orice rotație dublă (inclusiv una izoclinică) poate fi văzută ca doua rotații simple a și b: dubla rotație la stânga ca a apoi b, iar dubla rotație la dreapta ca b apoi a. Rotațiile simple nu sunt comutative; rotațiile la stânga și la dreapta (în general) ajung la destinații diferite. Diferența dintre o rotație dublă și cele două rotații simple care o compun este că rotația dublă este o diagonală cvadridimensională: ajunge la destinație direct fără a trece prin punctul intermediar atins de a apoi b, sau celălalt punct intermediar atins de b apoi de a, prin rotirea pe o singură geodezică elicoidală (deci este calea cea mai scurtă).^{[lower-alpha 53]} Invers, orice rotație simplă poate fi văzută ca o compunere a două rotații duble „cu unghiuri egale” (o rotație izoclinică la stânga și o rotație izoclinică la dreapta), așa cum a descoperit Cayley; Poate surprinzător, această compunere este comutativă și este posibilă și pentru orice rotație dublă.^[33]
55. Într-o rotație izoclinică, toate planele invariante paralele Clifford^{[lower-alpha 18]} sunt deplasate simultan în patru direcții ortogonale (două plane complet ortogonale): sunt rotite cu același unghi și, în același timp, sunt înclinate în lateral cu același unghi. O deplasare Clifford este o diagonală 4-dimensională.^{[lower-alpha 55]} Fiecare plan care este paralel Clifford cu unul dintre planele complet ortogonale (inclusiv în acest caz un întreg pachet paralel Clifford de 4 hexagoane, dar nu toate cele 16 hexagoane) este invariant în cazul rotației izoclinice: toate punctele din plan se rotesc în cercuri, dar rămân în plan, chiar dacă întregul plan se mișcă lateral. Toate cele 16 hexagoane se rotesc cu același unghi (deși doar 4 din ele o fac invariabil). Toate cele 16 hexagoane sunt rotite cu 60° și deplasate și lateral cu 60° către un hexagon paralel Clifford. Toate celelalte poligoane centrale (de exemplu, pătratele) sunt, de asemenea, mutate într-un poligon paralel Clifford la 60° distanță.
56. O rotație în spațiul euclidian cvadridimensional este caracterizată complet prin alegerea unui plan invariant, al unui unghi și direcție (stânga sau dreapta) cu care se rotește și a unui alt unghi și direcție cu care se rotește planul invariant complet ortogonal. Două deplasări prin rotație sunt identice dacă au aceeași pereche de plane invariante de rotație, cu aceleași unghiuri în aceleași direcții (și deci și aceeași pereche chirală). Astfel, rotația generală în spațiile cvadridimensionale este o rotație dublă. O rotație simplă este un caz particular în care un unghi de rotație este de 0°.^{[lower-alpha 54]} O rotație izoclinică este un caz particular diferit, asemănător dar nu identic cu doua rotații simple cu același unghi, una la stânga și alta la dreapta.^{[lower-alpha 55]}
57. Într-o rotație izoclinică fiecare punct al 4-politopului se deplasează la o distanță egală în două direcții ortogonale simultan, pe o diagonală 4-dimensională.^{[lower-alpha 29]} Punctul este deplasat o distanță euclidiană totală egală cu rădăcina pătrată a de două ori acea distanță. De exemplu, atunci când raza unitate a 24-celule se rotește izoclinic cu 60° în planele invariante hexagonale și 60° în planul său invariant complet ortogonal,^{[lower-alpha 35]} fiecare vârf este deplasat la un alt vârf la distanța de √2 raze (90°) în două coordonate ortogonale.
58. Acest prim vârf atins este la 90° de-a lungul unei coarde √2, dar nici rotația izoclinică nu se limitează la un plan pătratic: al doilea vârf atins va fi la 90° de grade într-un alt plan pătrat.
59. Deoarece geodezica elicoidală dodecagramică₂ a 24-celule este îndoită în a patra dimensiune într-un inel răsucit ca o bandă Möbius, filetul său revine înapoi după fiecare rotație, fără a-și inversa direcția de rotație (stânga sau dreapta). Calea izoclinică prin 12 vârfuri formează o spirală dublă Möbius (ca o spirală dublă tridimensională, dar cu capetele opuse ale celor două elice prin 6 vârfuri unite). Ea trece prin vârfurile neadiacente ale dodecagonului Petrie strâmb (în zigzag) al 24-celule așa cum trece și poligonul, dar, spre deosebire de poligonul Petrie, ea nu merge în zigzag, ci se îndoaie întotdeauna fie la dreapta, fie la stânga, de-a lungul unei „drepte” geodezice elicoidale chirale sau a unei izocline.^{[lower-alpha 29]} Poligonul strâmb ale cărui vârfuri se află pe această geodezică izoclinică este un dodecagon strâmb cu frecvență mai mică (lungime de undă mai mare) decât poligonul Petrie: vârfurile sale sunt cele al unei dodecagrame compuse {12/2} = 2{6}, nu al unui dodecagon regulat strâmb în zigzag. Dodecagonul Petrie are laturi √1 care merg în zigzag; dodecagrama₂ izoclinică are laturi √2 de-a lungul unei spirale geodezice (fie pe stânga, fie pe dreapta) conectând vârfurile distanțate la 2 ale dodecagramei₂ strâmbe care merge fie în zig, fie în zag (de-a lungul unei spirale geodezice pe stânga sau pe dreapta). Cele două fire elicolidale ale dublei elice continue în buclă sunt separate la √1 pentru fiecare pereche de vârfuri proxime: sunt paralele Clifford.^{[lower-alpha 18]} Fiecare latură √2 aparține unui pătrat mare diferit, iar laturile succesive √2 aparțin unor 16-celule diferite, așa cum rotația izoclinică duce pătrate la pătrate paralele Clifford și trece prin 16-celule paralele Clifford succesive.^{[lower-alpha 32]}
60. Toate planele izoclinice sunt paralele Clifford (complet disjuncte).^{[lower-alpha 42]} Celulele și 4-politopurile pot fi izoclinice și nedisjuncte dacă toate planele lor corespondente sunt fie paralele Clifford, sau cocelulare (în același hiperplan) sau coincidente.
61. Prin generare se înțelege pur și simplu că un vârf al primului politop va vizita fiecare vârf al politopului generat în cursul rotației.
62. Ca o cheie care acționează o încuietoare cvadridimensională, un obiect trebuie să se răsucească în doi cilindri complet perpendiculari pentru a deplasa distanța scurtă dintre subspațiile paralele Clifford.

Note

1. Coxeter 1973, p. 118, Chapter VII: Ordinary Polytopes in Higher Space.
2. Johnson 2018, p. 249, 11.5.
3. Coxeter 1973, pp. 292-293, Table I(ii): The sixteen regular polytopes {p,q,r} in four dimensions.
4. Coxeter 1973, p. 302, Table VI (ii): 𝐈𝐈 = {3,4,3}. : see Result column
5. Coxeter 1973, p. 156, §8.7. Cartesian Coordinates.
6. Coxeter 1973, pp. 145-146, §8.1 The simple truncations of the general regular polytope.
7. Coxeter 1973, p. 298, Table V: The Distribution of Vertices of Four-Dimensional Polytopes in Parallel Solid Sections (§13.1); (i) Sections of {3,4,3} (edge 2) beginning with a vertex; see column a.
8. Stillwell 2001, p. 17.
9. Tyrrell & Semple 1971, pp. 5-6, §3. Clifford's original definition of parallelism.
10. Kim & Rote 2016, pp. 8-10, Relations to Clifford Parallelism.
11. Copher 2019, p. 6, §3.2 Teorema 3.4.
12. Kim & Rote 2016, p. 7, §6 Angles between two Planes in 4-Space.
13. Coxeter 1973, p. 153, 8.5. Gosset's construction for {3,3,5}. : "In fact, the vertices of {3,3,5}, each taken 5 times, are the vertices of 25 {3,4,3}'s."
14. Coxeter 1973, p. 304, Table VI(iv) II={5,3,3}. : Faceting {5,3,3}[120𝛼₄]{3,3,5} of the 120-cell reveals 120 regular 5-cells.
15. Coxeter 1973, p. 150, Gosset.
16. Coxeter 1973, p. 148, §8.2. Cesaro's construction for {3, 4, 3}..
17. Coxeter 1973, p. 302, Table VI(ii) II={3,4,3}, Result column.
18. Coxeter 1973, pp. 149-150, §8.22. see illustrations Fig. 8.2A and Fig 8.2B.
19. Kepler 1619, p. 181.
20. van Ittersum 2020, pp. 73-79, §4.2.
21. Coxeter 1973, p. 269, §14.32. . "For instance, in the case of ${\displaystyle \gamma _{4}[2\beta _{4}]}$...."
22. Coxeter 1973, pp. 292-293, Table I(ii) The sixteen regular polytopes {p,q,r} in four dimensions. : [An invaluable table providing all 20 metrics of each 4-polytope in edge length units. They must be algebraically converted to compare polytopes of unit radius.]
23. van Ittersum 2020, p. 79.
24. Coxeter 1973, p. 150. : "Thus the 24 cells of the {3, 4, 3} are dipyramids based on the 24 squares of the ${\displaystyle \gamma _{4}}$. (Their centres are the mid-points of the 24 edges of the ${\displaystyle \beta _{4}}$.)"
25. Coxeter 1973, p. 12, §1.8. Configurations.
26. Coxeter 1973, p. 120, §7.2.. : "... any n+1 points which do not lie in an (n-1)-space are the vertices of an n-dimensional simplex.... Thus the general simplex may alternatively be defined as a finite region of n-space enclosed by n+1 hyperplanes or (n-1)-spaces."
27. van Ittersum 2020, p. 78, §4.2.5.
28. Stillwell 2001, p. 22.
29. Coxeter 1973, p. 163. : Coxeter notes that Gosset was apparently the first to see that the cells of the 24-cell honeycomb {3,4,3,3} are concentric with alternate cells of the tesseractic honeycomb {4,3,3,4}, and that this observation enabled Gosset's method of construction of the complete set of regular polytopes and honeycombs.
30. Coxeter 1973, p. 156. : "...the chess-board has an n-dimensional analogue."
31. Coxeter 1973, p. 119, §7.1. Dimensional Analogy. : "For instance, seeing that the circumference of a circle is 2π r, while the surface of a sphere is 4π r ², ... it is unlikely that the use of analogy, unaided by computation, would ever lead us to the correct expression, 2π ²r ³."
32. Kim & Rote 2016, p. 6, §5. Four-Dimensional Rotations.
33. en Perez-Gracia, Alba; Thomas, Federico (2017). „On Cayley's Factorization of 4D Rotations and Applications” (PDF). Adv. Appl. Clifford Algebras. 27: 523–538. doi:10.1007/s00006-016-0683-9. hdl:2117/113067 .
34. Kim & Rote 2016, pp. 7–10, §6. Angles between two Planes in 4-Space.
35. Coxeter 1995, (Paper 3) Two aspects of the regular 24-cell in four dimensions.
36. Kim & Rote 2016, pp. 8-9, Relations to Clifford parallelism.
37. Tyrrell & Semple1971, pp. 1-9, §1. Introduction.
38. Banchoff 2013, pp. 265–266.
39. Coxeter 1991.

Bibliografie

• la Kepler, Johannes (1619). Harmonices Mundi. Johann Planck.
• en Coxeter, H.S.M. (1973) [1948]. Regular Polytopes (ed. 3rd). New York: Dover.
• en Coxeter, H.S.M. (1991), Regular Complex Polytopes (ed. 2nd), Cambridge: Cambridge University Press
• en Coxeter, H.S.M. (1995), Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic, ed., Kaleidoscopes: Selected Writings of H.S.M. Coxeter (ed. 2nd), Wiley-Interscience Publication, ISBN 978-0-471-01003-6

• (Paper 3) H.S.M. Coxeter, Two aspects of the regular 24-cell in four dimensions
• (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
• (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
• (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]

• en Stillwell, John (ianuarie 2001). „The Story of the 120-Cell” (PDF). Notices of the AMS. 48 (1): 17–25.
• en Johnson, Norman (2018), Geometries and Transformations, Cambridge: Cambridge University Press, ISBN 978-1-107-10340-5
• en Johnson, Norman (1991), Uniform Polytopes (ed. Manuscript)
• en Johnson, Norman (1966), The Theory of Uniform Polytopes and Honeycombs (ed. Ph.D.)
• en Eric W. Weisstein, 24-Cell la MathWorld. (also under Icositetrachoron)
• en Klitzing, Richard. „4D uniform polytopes (polychora) x3o4o3o - ico”.
• en George Olshevsky. „Icositetrachoron”. Glossary for Hyperspace. Arhivat din original la 4 februarie 2007.

• [3,4,3]: Icositetrachoron (22)
• [4,3,3]: Rectified 16-cell (22)
• [3^1,1,1]: Icositetrachoron (22)

• Ghyka, Matila (1977). The Geometry of Art and Life. New York: Dover Publications. ISBN 978-0-486-23542-4.
• en Banchoff, Thomas F. (2013). „Torus Decompostions of Regular Polytopes in 4-space”. În Senechal, Marjorie. Shaping Space. Springer New York. pp. 257–266. doi:10.1007/978-0-387-92714-5_20. ISBN 978-0-387-92713-8.
• en van Ittersum, Clara (2020). Symmetry groups of regular polytopes in three and four dimensions (Teză). Delft University of Technology.
• en Davoust, Emmanuel. "A hundred years of science at the Pic du Midi Observatory". arXiv:astro-ph/9707201
• en Tyrrell, J. A.; Semple, J.G. (1971). Generalized Clifford parallelism. Cambridge University Press. ISBN 0-521-08042-8.
• de Der 24-Zeller (24-cell) Marco Möller's Regular polytopes in R⁴

Legături externe

• Materiale media legate de 24-celule la Wikimedia Commons
• en 24-cell animations
• en 24-cell in stereographic projections Arhivat în 13 septembrie 2020, la Wayback Machine.
• en 24-cell description and diagrams Arhivat în 15 iulie 2007, la Wayback Machine.
• en Petrie dodecagons in the 24-cell: mathematics and animation software

	Portal Matematică

v • d • m Politopuri regulate și uniforme convexe fundamentale în dimensiunile 2–10
An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Triunghi	Pătrat	p-gon	Hexagon	Pentagon
Tetraedru	Octaedru • Cub	Semicub		Dodecaedru • Icosaedru
5-celule	16-celule • Tesseract	Semitesseract	24-celule	120-celule • 600-celule
5-simplex	5-ortoplex • 5-cub	5-semicub
6-simplex	6-ortoplex • 6-cub	6-semicub	122 • 221
7-simplex	7-ortoplex • 7-cub	7-semicub	132 • 231 • 321
8-simplex	8-ortoplex • 8-cub	8-semicub	142 • 241 • 421
9-simplex	9-ortoplex • 9-cub	9-semicub
10-simplex	10-ortoplex • 10-cub	10-semicub
n-simplex	n-ortoplex • n-cub	n-semicub	1k2 • 2k1 • k21	n-politop pentagonal
Topicuri: Familii de politopuri • Politop regulat