Współrzędne krzywoliniowe

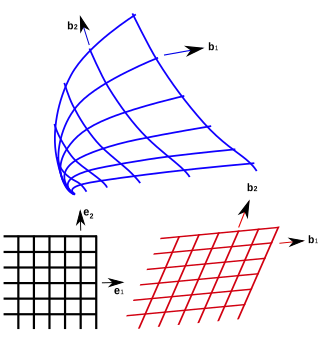
Współrzędne krzywoliniowe mogą być określone w przestrzeni euklidesowej ${\displaystyle E^{n}}$ o dowolnym, skończonym wymiarze ${\displaystyle n.}$ Tworzą one ${\displaystyle n}$ rodzin linii (w ogólnym przypadku linii krzywych) w postaci regularnych siatek przestrzennych (rys. 1).

Rys. 1. Układy współrzędnych w przestrzeni 2-wymiarowej: krzywoliniowy (u góry), afiniczny (z prawej), kartezjański (z lewej).

Najczęściej spotykanymi są współrzędne:

• prostokątne (kartezjańskie),
• ukośnokątne (afiniczne),
• biegunowe,
• cylindryczne,
• sferyczne.

Aby wprowadzić jakieś współrzędne krzywoliniowe, w danej przestrzeni euklidesowej, trzeba podać odpowiednie wzory transformacyjne opisujące sposób przejścia do tych nowych współrzędnych od starych współrzędnych kartezjańskich. Wymaga się przy tym:

(1) aby współrzędnym kartezjańskim punktów przestrzeni ${\displaystyle E^{n}}$ odpowiadały unikalne wartości ${\displaystyle n}$ współrzędnych krzywoliniowych. Dlatego wzory transformacyjne muszą być opisane funkcjami wzajemnie jednoznacznymi. Ta bijekcja nie zawsze jest możliwa w całej przestrzeni ${\displaystyle E^{n},}$

(2) aby funkcje transformujące były różniczkowalne dostateczną liczbę razy dzięki czemu staje się możliwe zdefiniowanie bogatszej struktury, np. wprowadzenie lokalnych baz wektorów w każdym punkcie dziedziny, co pozwala na definiowanie pól wektorowych czy też tensorowych i wykonywanie na nich operacji różniczkowania i całkowania.

Nazwa „współrzędne krzywoliniowe” została wprowadzona przez francuskiego matematyka Gabriela Lamé. Formalizm współrzędnych krzywoliniowych został uogólniony na przestrzenie nieeuklidesowe, m.in. przez Riemanna.

W tym artykule zagadnienie współrzędnych krzywoliniowych omówiono na przykładzie przestrzeni 3-wymiarowej, która jest dobrym modelem przestrzeni fizycznej (podobnie omawia to np. ^[1]). Zaletą takiego podejścia jest to, że podane w nim pojęcia i metody obliczeniowe w sposób naturalny dają się uogólnić na przestrzenie euklidesowe dowolnego wymiaru. Nieznaczne zaś rozszerzenie formalizmu poprzez dopuszczenie dowolnej postaci tensora metrycznego pozwala łatwo przejść do opisu geometrii nieeuklidesowych.

Zastosowania

Układy współrzędnych krzywoliniowych znajdują liczne zastosowania np.:

• w teoriach pól fizycznych (skalarnych, wektorowych i tensorowych); pojawiające się w analizie tych pól wielkości geometryczne, takie jak gradient, dywergencja, rotacja, laplasjan itp. wyraża się we współrzędnych krzywoliniowych, wychodząc od definicji tych wielkości we współrzędnych kartezjańskich i po wykorzystaniu wzorów transformacyjnych. Otrzymanym wyrażeniom nadaje się postać uniwersalną, obowiązującą w dowolnym układzie krzywoliniowym;
• w mechanice klasycznej i w mechanice kwantowej przy rozwiązywaniu zagadnień ruchu ciał poddanych działaniu sił centralnych użycie układu krzywoliniowego upraszcza opis ruchu (np. opis ruchu planet wokół gwiazdy centralnej, czy ruchu elektronu wokół jądra atomu – model atomu Bohra w układzie sferycznym);
• w ogólnej teorii względności – użycie współrzędnych krzywoliniowych jest niezbędne, gdyż efektem działania pól grawitacyjnych jest zakrzywienie czasoprzestrzeni. Nie da się ściśle opisać ani pól grawitacyjnych, ani trajektorii ciał poruszających się w tych polach, za pomocą współrzędnych prostokątnych; np. ciała w polach grawitacyjnych poruszają się po liniach geodezyjnych, które nie są prostymi euklidesowymi.

Współrzędne krzywoliniowe w przestrzeni euklidesowej 3D

(1) Niech w trójwymiarowej przestrzeni euklidesowej ${\displaystyle E^{3},}$ z wprowadzonym w niej układem kartezjańskim ${\displaystyle Ox^{1}x^{2}x^{3},}$ będzie dany punkt ${\displaystyle P}$ opisany jego wektorem wodzącym ${\displaystyle {\vec {r}}(x^{1},x^{2},x^{3})}$ zależnym od trzech parametrów ${\displaystyle q^{1},q^{2},q^{3},}$ tj.

${\displaystyle {\vec {r}}=x^{1}{\vec {e}}_{1}+x^{2}{\vec {e}}_{2}+x^{3}{\vec {e}}_{3},}$

gdzie: ${\displaystyle {\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3}}$ są wersorami bazy przyjętego układu współrzędnych kartezjańskich oraz

${\displaystyle x^{1}=x^{1}(q^{1},q^{2},q^{3}),}$ ${\displaystyle x^{2}=x^{2}(q^{1},q^{2},q^{3}),}$ ${\displaystyle x^{3}=x^{3}(q^{1},q^{2},q^{3}),}$

(1)

przy czym funkcje ${\displaystyle x^{i}=x^{i}(q^{1},q^{2},q^{3}),\;i=1,2,3}$ są klasy ${\displaystyle C_{1},}$ tj. mają ciągłe pierwsze pochodne cząstkowe.

(2) Definicja: Parametry ${\displaystyle q^{1},q^{2},q^{3}}$ nazywamy współrzędnymi krzywoliniowymi punktu ${\displaystyle P,}$ jeżeli istnieje wzajemnie jednoznaczna odpowiedniość (1) pomiędzy nimi, a współrzędnymi kartezjańskimi ${\displaystyle x^{1},x^{2},x^{3}}$ punktu ${\displaystyle P,}$ przy czym wymaga się, by poniższy jakobian był różny od zera dla punktów ${\displaystyle (q^{1},q^{2},q^{3})\in D,}$ gdzie ${\displaystyle D}$ – zbiór, na jakim chce się wprowadzić współrzędne krzywoliniowe, tj.^[2]

${\displaystyle \left|{\frac {\partial x^{i}}{\partial q^{\alpha }}}\right|\equiv \left|{\frac {\partial (x^{1},x^{2},x^{3})}{\partial (q^{1},q^{2},q^{3})}}\right|\equiv }$

${\displaystyle {}\qquad \equiv \left|{\begin{matrix}{\frac {\partial x^{1}}{\partial q^{1}}}&{\frac {\partial x^{1}}{\partial q^{2}}}&{\frac {\partial x^{1}}{\partial q^{3}}}\\{\frac {\partial x^{2}}{\partial q^{1}}}&{\frac {\partial x^{2}}{\partial q^{2}}}&{\frac {\partial x^{2}}{\partial q^{3}}}\\{\frac {\partial x^{3}}{\partial q^{1}}}&{\frac {\partial x^{3}}{\partial q^{2}}}&{\frac {\partial x^{3}}{\partial q^{3}}}\end{matrix}}\right|\neq 0\,\,{\text{dla}}\,\,(q^{1},q^{2},q^{3})\in D.}$

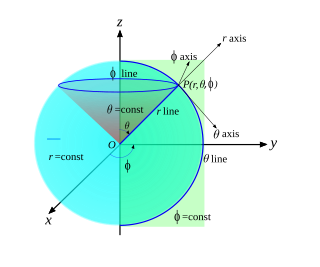
Warunek niezerowania się jakobianu oznacza, że w każdym punkcie rozważanego obszaru ${\displaystyle D}$ będzie można wprowadzić 3 osie lokalnego układu współrzędnych, styczne do linii współrzędnych i parami nierównoległe (por. rys. 2).

Rys. 2. Powierzchnie współrzędnych, krzywe współrzędnych, osie współrzędnych dowolnego układu współrzędnych krzywoliniowych.

(3) Warunek równoważny: Jakobian transformacji odwrotnej o składowych ${\displaystyle q^{\alpha }=q^{\alpha }(x^{1},x^{2},x^{3}),\,\,\alpha =1,2,3}$ musi być różny od zera dla punktów ${\displaystyle (x^{1},x^{2},x^{3})\in f(D),}$ gdzie ${\displaystyle f(D)}$ – obraz zbioru ${\displaystyle D}$ w transformacji ${\displaystyle f}$ dokonującej przejścia od współrzędnych krzywoliniowych do kartezjańskich.

(4) Definicja: Mówi się, że funkcje ${\displaystyle x^{i}=x^{i}(q^{1},q^{2},q^{3}),\;i=1,2,3}$ wprowadzają w przestrzeni krzywoliniowy układ współrzędnych.

(5) Definicja: Krzywe współrzędnych. Siatka współrzędnych krzywoliniowych

a) Ustalając wartości dwu nowych współrzędnych, a zmieniając wartość pozostałej, otrzymuje się krzywą w przestrzeni opisaną parametrycznie za pomocą zmieniającej się wartości współrzędnej, np.

${\displaystyle {\vec {r}}(q^{1},b,c)}$

przedstawia krzywą współrzędnych ${\displaystyle q^{1}}$ przy ustalonych wartościach współrzędnych ${\displaystyle q^{2}=b}$ oraz ${\displaystyle q^{3}=c.}$

b) Zmieniając wartości ${\displaystyle b,c}$ współrzędnych ${\displaystyle q^{2},\ q^{3},}$ otrzymuje się różne linie siatki współrzędnej ${\displaystyle q^{1}.}$

c) Postępując podobnie dla pozostałych współrzędnych, uzyskuje się wszystkie linie siatki współrzędnych krzywoliniowych.

d) Przez każdy punkt ${\displaystyle P(a,b,c)}$ przechodzą trzy przecinające się wzajemnie linie współrzędnych ${\displaystyle {\vec {r}}(q^{1},b,c),}$ ${\displaystyle {\vec {r}}(a,q^{2},c),}$ ${\displaystyle {\vec {r}}(a,b,q^{3}).}$

Przykład: Współrzędne sferyczne r , ϕ , θ {\displaystyle r,\phi ,\theta }

Rys. 3. Powierzchnie współrzędnych, krzywe współrzędnych i osie współrzędnych dla współrzędnych sferycznych. Powierzchnie: r – sfery, θ – stożki, φ – półpłaszczyzny. Krzywe: r – proste idące promieniście, θ – pionowe półokręgi, φ – poziome okręgi. Osie: r – proste idące promieniście, θ – styczne do pionowych półokręgów, φ – styczne do poziomych okręgów.

(1) Współrzędne sferyczne ${\displaystyle r,\phi ,\theta }$ są zdefiniowane przez następujące funkcje współrzędnych kartezjańskich ${\displaystyle x,y,z{:}}$

${\displaystyle r=r(x,y,z)\equiv {\sqrt {x^{2}+y^{2}+z^{2}}},}$

${\displaystyle \phi =\phi (x,y,z)\equiv \mathrm {arctg} {\frac {y}{x}},}$

${\displaystyle \theta =\theta (x,y,z)\equiv \mathrm {arctg} {\frac {\sqrt {x^{2}+y^{2}}}{z}},}$

przy czym: ${\displaystyle x\neq 0,\;y\neq 0,\;z\neq 0,}$

${\displaystyle r\in (0,+\infty ),\quad \phi \in [0,2\pi ),\quad \theta \in (0,\pi ).}$

(2) Konwersję ze współrzędnych sferycznych na współrzędne kartezjańskie ${\displaystyle x,y,z}$ określają wzory odwrotne:

${\displaystyle x=x(r,\theta ,\phi )\equiv r\,\sin \theta \,\cos \phi ,}$

${\displaystyle y=y(r,\theta ,\phi )\equiv r\,\sin \theta \,\sin \phi ,}$

${\displaystyle z=z(r,\theta ,\phi )\equiv r\,\cos \theta .}$

(3) Jakobian przejścia

${\displaystyle {\frac {\partial (x,y,z)}{\partial (r,\theta ,\phi )}}=\left|{\begin{array}{c}{\frac {\partial x}{\partial r}}&{\frac {\partial x}{\partial \theta }}&{\frac {\partial x}{\partial \phi }}\\{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \theta }}&{\frac {\partial y}{\partial \phi }}\\{\frac {\partial z}{\partial r}}&{\frac {\partial z}{\partial \theta }}&{\frac {\partial z}{\partial \phi }}\end{array}}\right|=}$

${\displaystyle =\left|{\begin{array}{c}\sin \theta \cos \phi &r\cos \theta \cos \phi &-r\sin \theta \sin \phi \\\sin \theta \sin \phi &r\cos \theta \sin \phi &r\sin \theta \cos \phi \\\cos \theta &-r\sin \theta &0\end{array}}\right|=r^{2}\sin \theta .}$

W punktach, gdzie jakobian jest różny od zera można wprowadzić lokalne układy wektorów bazowych, styczne do linii współrzędnych (por. rys. 4).

Współrzędne kontrawariantne i kowariantne

Rys. 4. Wektor v rozłożony w dwóch bazach:
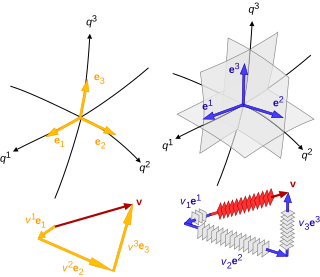
(1) baza wersorów ${\displaystyle {\hat {g}}_{1},{\hat {g}}_{2},{\hat {g}}_{3}}$ (żółta, z lewej) – stycznych do krzywych współrzędnych (czarne)
(2) kobaza wersorów ${\displaystyle {\hat {g}}^{1},{\hat {g}}^{2},{\hat {g}}^{3}}$ (niebieska, z prawej) – prostopadłych do powierzchni współrzędnych (szare).
Wersory bazy i kobazy nie są do siebie równoległe, chyba że współrzędne (q¹, q², q³) są ortogonalne.

Mając dany układ współrzędnych krzywoliniowych, można określić dla niego, w każdym punkcie przestrzeni, lokalne wersory osi, przy czym można to zrobić na dwa różne sposoby:

1. wersory bazy ${\displaystyle ({\hat {g}}_{1},{\hat {g}}_{2},{\hat {g}}_{3})}$ są styczne do linii współrzędnych, przechodzących przez dany punkt. Współrzędne ${\displaystyle r^{1},r^{2},r^{3}}$ wektora reprezentowanego w tej bazie nazywa się jego współrzędnymi kontrawariantnymi (przeciwzmienniczymi). Tę bazę nazywa się także bazą wektorów kontrawariantnych;
2. wersory kobazy ${\displaystyle ({\hat {g}}^{1},{\hat {g}}^{2},{\hat {g}}^{3}),}$ zwanej też bazą dualną, są normalne do płaszczyzn współrzędnych przechodzących przez dany punkt. Współrzędne ${\displaystyle r_{1},r_{2},r_{3}}$ wektora reprezentowanego w kobazie nazywa się jego współrzędnymi kowariantnymi (współzmienniczymi). Tę bazę nazywa się również bazą wektorów kowariantnych;
3. dowolny wektor w ${\displaystyle E^{3}}$ można zapisać dwojako
   

${\displaystyle {}\qquad \qquad {\vec {v}}=v^{\alpha }{\hat {g}}_{\alpha }=v_{\alpha }{\hat {g}}^{\alpha },\qquad \alpha =1,2,3.}$

W układzie współrzędnych kartezjańskich baza i kobaza są identyczne: ${\displaystyle ({\hat {e}}_{1},{\hat {e}}_{2},{\hat {e}}_{3})\equiv ({\hat {e}}^{1},{\hat {e}}^{2},{\hat {e}}^{3}).}$

Aby odróżnić współrzędne kontrawariantne od kowariantnych stosuje się umowę:

1. współrzędnym kontrawariantnym (liczonym względem bazy) przypisuje się wskaźniki górne,
2. współrzędnym kowariantnym (liczonym względem kobazy) przypisuje się wskaźniki dolne.

Własności bazy i kobazy

(1) Wektory bazy i kobazy dla dowolnego układu współrzędnych krzywoliniowych, pozwala obliczać uniwersalna procedura (patrz niżej).

(2) Współrzędne nazywa się ortogonalnymi, jeżeli linie współrzędnych przecinają się pod kątami prostymi. Np. współrzędne sferyczne, walcowe, biegunowe są ortogonalne.

(3) Wektory bazy (i kobazy) współrzędnych ortogonalnych są ortogonalne. W takim przypadku wektory bazy i kobazy są parami równoległe do siebie.

(4) Wybór bazy pozwala wykonywać w niej obliczenia, np.

• dowolne pole wektorowe ${\displaystyle {\vec {r}}(x^{1},x^{2},x^{3})}$ może być rozłożone na składowe przez rzutowanie:

• na wektory bazy – wtedy pole to ma współrzędne kontrawariantne – ${\displaystyle r^{1},r^{2},r^{3}}$ lub
• na wektory kobazy – wtedy pole ma współrzędne kowariantne – ${\displaystyle r_{1},r_{2},r_{3};}$

• współrzędne pola są zazwyczaj funkcjami różniczkowalnymi (zależnymi od punktów przestrzeni) – dzięki temu możliwe jest wykonywanie obliczeń, np. obliczanie zmian pola w zadanych warunkach, korzystając z równań pola (np. równań Maxwella, równań Einsteina).

Baza wektorów kontrawariantnych

Obliczanie bazy wektorów kontrawariantnych

(1) W każdym nieosobliwym punkcie ${\displaystyle {\vec {r}}(x^{1},x^{2},x^{3})}$ rozpatrywanego obszaru ${\displaystyle D}$ można zdefiniować trzy wektory bazowe ${\displaystyle {\vec {g}}_{1},{\vec {g}}_{2},{\vec {g}}_{3}}$ styczne odpowiednio do krzywych ${\displaystyle q^{1},q^{2},q^{3}}$ przy ustalonych wartościach dwóch pozostałych nowych współrzędnych ${\displaystyle {\vec {g}}_{1}={\tfrac {\partial {\vec {r}}}{\partial q^{1}}}=\left[{\tfrac {\partial x^{1}}{\partial q^{1}}},{\tfrac {\partial x^{2}}{\partial q^{1}}},{\tfrac {\partial x^{3}}{\partial q^{1}}}\right]={\tfrac {\partial x^{1}}{\partial q^{1}}}{\vec {e}}_{1}+{\tfrac {\partial x^{2}}{\partial q^{1}}}{\vec {e}}_{2}+{\tfrac {\partial x^{3}}{\partial q^{1}}}{\vec {e}}_{3},}$

${\displaystyle {\vec {g}}_{2}={\tfrac {\partial {\vec {r}}}{\partial q^{2}}}=\left[{\tfrac {\partial x^{1}}{\partial q^{2}}},{\tfrac {\partial x^{2}}{\partial q^{2}}},{\tfrac {\partial x^{3}}{\partial q^{2}}}\right]={\tfrac {\partial x^{1}}{\partial q^{2}}}{\vec {e}}_{1}+{\tfrac {\partial x^{2}}{\partial q^{2}}}{\vec {e}}_{2}+{\tfrac {\partial x^{3}}{\partial q^{2}}}{\vec {e}}_{3},}$

${\displaystyle {\vec {g}}_{3}={\tfrac {\partial {\vec {r}}}{\partial q^{3}}}=\left[{\tfrac {\partial x^{1}}{\partial q^{3}}},{\tfrac {\partial x^{2}}{\partial q^{3}}},{\tfrac {\partial x^{3}}{\partial q^{3}}}\right]={\tfrac {\partial x^{1}}{\partial q^{3}}}{\vec {e}}_{1}+{\tfrac {\partial x^{2}}{\partial q^{3}}}{\vec {e}}_{2}+{\tfrac {\partial x^{3}}{\partial q^{3}}}{\vec {e}}_{3},}$

gdzie:

${\displaystyle {\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3}}$ – wektory ortonormalne układu współrzędnych kartezjańskich.

(2) Z powyższych wzorów widać, że:

Baza układu kartezjańskiego transformuje się w bazę układu krzywoliniowego za pomocą macierzy transformacji

${\displaystyle \Lambda _{\alpha }^{i}(x^{i}\to q^{\alpha })=\left[{\frac {\partial x^{i}}{\partial q^{\alpha }}}\right],\qquad i,\alpha =1,2,3.}$

Elementami tej macierzy są pochodne współrzędnych kartezjańskich względem współrzędnych krzywoliniowych, obliczone w danym punkcie obszaru ${\displaystyle D.}$ Macierze transformacji obliczone w różnych punktach przestrzeni będą mieć więc na ogół różne elementy.

Macierz transformacji ma istotne znaczenie w określaniu własności transformacyjnych obiektów geometrycznych (wektorów, tensorów), określonych w danym punkcie obszaru ${\displaystyle D.}$

(3) Niezerowanie się jakobianu gwarantuje, że wektory ${\displaystyle {\vec {g}}_{1},{\vec {g}}_{2},{\vec {g}}_{3}}$ są nierównoległe do siebie, a więc tworzą bazę. W skrócie wektory te można zapisać jednym wyrażeniem ${\displaystyle {\vec {g}}_{\alpha }={\tfrac {\partial {\vec {r}}}{\partial q^{\alpha }}}=\left[{\tfrac {\partial x^{1}}{\partial q^{\alpha }}},{\tfrac {\partial x^{2}}{\partial q^{\alpha }}},{\tfrac {\partial x^{3}}{\partial q^{\alpha }}}\right]={\tfrac {\partial x^{1}}{\partial q^{\alpha }}}{\vec {e}}_{1}+{\tfrac {\partial x^{2}}{\partial q^{\alpha }}}{\vec {e}}_{2}+{\tfrac {\partial x^{3}}{\partial q^{\alpha }}}{\vec {e}}_{3},\quad \alpha =1,2,3}$

lub stosując konwencję sumacyjną Einsteina

${\displaystyle {\vec {g}}_{\alpha }={\frac {\partial x^{j}}{\partial q^{\alpha }}}{\vec {e}}_{j},\quad \alpha =1,2,3,}$

(2)

gdzie sumuje się po powtarzającym się wskaźniku ${\displaystyle j,}$ przyjmując ${\displaystyle j=1,2,3.}$

(4) Nieznikanie jakobianu w każdym punkcie gwarantuje też, że istnieje wzór odwrotny

${\displaystyle {\vec {e}}_{j}={\frac {\partial q^{\alpha }}{\partial x^{j}}}{\vec {g}}_{\alpha },\quad j=1,2,3}$

(3)

gdzie sumuje się po powtarzającym się wskaźniku ${\displaystyle \alpha ,}$ przyjmując ${\displaystyle \alpha =1,2,3.}$

(5) Wzory (2) i (3) realizują wzajemne transformacje pomiędzy bazami: ${\displaystyle ({\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3})}$ i ${\displaystyle ({\vec {g}}_{1},{\vec {g}}_{2},{\vec {g}}_{3}).}$

(6) Macierz ${\displaystyle \Lambda _{i}^{\alpha }=\left[{\frac {\partial q^{\alpha }}{\partial x^{i}}}\right]}$ jest odwrotna do macierzy ${\displaystyle \Lambda _{\alpha }^{i}=\left[{\frac {\partial x^{i}}{\partial q^{\alpha }}}\right],}$ co oznacza, że słuszna jest zależność

${\displaystyle {\frac {\partial x^{i}}{\partial q^{\alpha }}}{\frac {\partial q^{\alpha }}{\partial x^{j}}}=\delta _{j}^{\,i},\quad i,j=1,2,3}$

– sumujemy tu po wskaźniku ${\displaystyle \alpha .}$

(7) Podobnie, słuszna jest zależność odwrotna

${\displaystyle {\frac {\partial q^{\beta }}{\partial x^{j}}}{\frac {\partial x^{j}}{\partial q^{\alpha }}}=\delta _{\alpha }^{\beta },\quad \alpha ,\beta =1,2,3}$

– sumujemy tu po wskaźniku ${\displaystyle j.}$

Uwaga: Wektory bazy ${\displaystyle {\vec {g}}_{1},{\vec {g}}_{2},{\vec {g}}_{3}}$ są styczne odpowiednio do linii współrzędnych ${\displaystyle q^{1},q^{2},q^{3}}$ – nie są jednak ortogonalne jeśli linie współrzędnych w danym punkcie nie przecinają się pod kątami prostymi. Ponadto wektory te nie są unormowane do ${\displaystyle 1,}$ co więcej – ich długość może zmieniać się ze zmianą położenia ${\displaystyle {\vec {r}}}$ w przestrzeni. Spośród wielu baz wygodne są bazy ortogonalne, gdyż łatwiej wykonywać w nich obliczenia.

Normowanie wektorów bazy

Wektory bazy łatwo unormować do ${\displaystyle 1{:}}$ po prostu dzieli się te wektory przez ich długość, którą oblicza się jako pierwiastek z iloczynu skalarnego wektora przez siebie:

${\displaystyle h_{1}={\sqrt {{\vec {g}}_{1}\cdot {\vec {g}}_{1}}}={\sqrt {\left({\frac {\partial x^{1}}{\partial q^{1}}}\right)^{2}+\left({\frac {\partial x^{2}}{\partial q^{1}}}\right)^{2}+\left({\frac {\partial x^{3}}{\partial q^{1}}}\right)^{2}}},}$

${\displaystyle h_{2}={\sqrt {{\vec {g}}_{2}\cdot {\vec {g}}_{2}}}={\sqrt {\left({\frac {\partial x^{1}}{\partial q^{2}}}\right)^{2}+\left({\frac {\partial x^{2}}{\partial q^{2}}}\right)^{2}+\left({\frac {\partial x^{3}}{\partial q^{2}}}\right)^{2}}},}$

${\displaystyle h_{3}={\sqrt {{\vec {g}}_{3}\cdot {\vec {g}}_{3}}}={\sqrt {\left({\frac {\partial x^{1}}{\partial q^{3}}}\right)^{2}+\left({\frac {\partial x^{2}}{\partial q^{3}}}\right)^{2}+\left({\frac {\partial x^{3}}{\partial q^{3}}}\right)^{2}}}.}$

Powyższe współczynniki noszą nazwę współczynników Lamego.

Unormowane wektory bazy (tzn. jej wersory) mają postać:

${\displaystyle {\hat {g}}_{1}={\frac {1}{h_{1}}}{\frac {\partial {\vec {r}}}{\partial q^{1}}},\quad {\hat {g}}_{2}={\frac {1}{h_{2}}}{\frac {\partial {\vec {r}}}{\partial q^{2}}},\quad {\hat {g}}_{3}={\frac {1}{h_{3}}}{\frac {\partial {\vec {r}}}{\partial q^{3}}}.}$

Przykład: Baza ortonormalna wektorów kontrawariantnych

Współrzędne sferyczne

(1) Współrzędne kartezjańskie ${\displaystyle x,y,z}$ są wyrażone przez współrzędne sferyczne wzorami

${\displaystyle x=r\,\sin \theta \,\cos \phi ,}$

${\displaystyle y=r\,\sin \theta \,\sin \phi ,}$

${\displaystyle z=r\,\cos \theta .}$

(2) Obliczamy wektory bazowe: ${\displaystyle {\vec {g}}_{r}={\tfrac {\partial {\vec {r}}}{\partial r}}=\left[{\tfrac {\partial x}{\partial r}},{\tfrac {\partial y}{\partial r}},{\tfrac {\partial z}{\partial r}}\right]=[\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta ],}$ ${\displaystyle {\vec {g}}_{\theta }={\tfrac {\partial {\vec {r}}}{\partial \theta }}=\left[{\tfrac {\partial x}{\partial \theta }},{\tfrac {\partial y}{\partial \theta }},{\tfrac {\partial z}{\partial \theta }}\right]=[r\cos \theta \cos \phi ,r\cos \theta \sin \phi ,-r\sin \theta ],}$ ${\displaystyle {\vec {g}}_{\phi }={\tfrac {\partial {\vec {r}}}{\partial \phi }}=\left[{\tfrac {\partial x}{\partial \phi }},{\tfrac {\partial y}{\partial \phi }},{\tfrac {\partial z}{\partial \phi }}\right]=[-r\sin \theta \sin \phi ,r\sin \theta \cos \phi ,0].}$

(3) Wektory te są ortogonalne, gdyż zerują się ich iloczyny skalarne

${\displaystyle {\vec {g}}_{r}\cdot {\vec {g}}_{\theta }=0,\quad {\vec {g}}_{r}\cdot {\vec {g}}_{\phi }=0,\quad {\vec {g}}_{\theta }\cdot {\vec {g}}_{\phi }=0,}$

co łatwo policzyć, mnożąc wektory przez siebie.

(4) Obliczamy długości wektorów ${\displaystyle {\vec {g}}_{r},{\vec {g}}_{\phi },{\vec {g}}_{\theta },}$ czyli współczynniki Lamego

${\displaystyle h_{r}={\sqrt {{\vec {g}}_{r}\cdot {\vec {g}}_{r}}}={\sqrt {(\sin \theta \cos \phi )^{2}+(\sin \theta \sin \phi )^{2}+(\cos \theta )^{2}}}=1,}$

${\displaystyle h_{\theta }={\sqrt {{\vec {g}}_{\theta }\cdot {\vec {g}}_{\theta }}}={\sqrt {(r\cos \theta \cos \phi )^{2}+(\dots )^{2}+(\dots )^{2}}}=r,}$

${\displaystyle h_{\phi }={\sqrt {{\vec {g}}_{\phi }\cdot {\vec {g}}_{\phi }}}={\sqrt {(-r\sin \theta \sin \phi )^{2}+(r\sin \theta \cos \phi )^{2}+0^{2}}}=r\sin \theta .}$

(5) Normujemy wektory ${\displaystyle {\vec {g}}_{r},{\vec {g}}_{\phi },{\vec {g}}_{\theta }}$ do ${\displaystyle 1,}$ dzieląc je przez ich długości

${\displaystyle {\hat {g}}_{r}={\frac {{\vec {g}}_{r}}{h_{r}}}=[\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta ],}$

${\displaystyle {\hat {g}}_{\theta }={\frac {{\vec {g}}_{\theta }}{h_{\theta }}}=[\cos \theta \cos \phi ,\cos \theta \sin \phi ,-\sin \theta ],}$

${\displaystyle {\hat {g}}_{\phi }={\frac {{\vec {g}}_{\phi }}{h_{\phi }}}=[-\sin \phi ,\cos \phi ,0].}$

Powyższe wektory tworzą bazę ortonormalną układu kontrawariantnych współrzędnych sferycznych. Widać, że współrzędne tych wektorów zależą tylko od współrzędnych ${\displaystyle \phi ,\theta }$ punktu ${\displaystyle {\vec {r}}=(r,\phi ,\theta ),}$ w którym wektory te tworzą bazę – styczną do linii współrzędnych sferycznych. Oznacza to, że dwie bazy wyznaczone dla dwu różnych punktów o współrzędnych ${\displaystyle (r_{1},\phi ,\theta )}$ i ${\displaystyle (r_{2},\phi ,\theta )}$ są identyczne.

(6) Skrętność układu wektorów bazy

Można sprawdzić, że mnożąc wektorowo wektor ${\displaystyle {\hat {g}}_{r}}$ przez wektor ${\displaystyle {\hat {g}}_{\theta },}$ otrzyma się wektor ${\displaystyle {\hat {g}}_{\phi },}$ tzn.

${\displaystyle {\hat {g}}_{r}\times {\hat {g}}_{\theta }={\hat {g}}_{\phi }}$

co oznacza, że wektory te ustawione w kolejności ${\displaystyle {\hat {g}}_{r},{\hat {g}}_{\theta },{\hat {g}}_{\phi }}$ tworzą bazę prawoskrętną.

Baza wektorów kowariantnych

Powierzchnie współrzędnych

a) Ustalając jedną z nowych współrzędnych, a zmieniając dwie pozostałe, otrzymuje się powierzchnię w przestrzeni opisaną parametrycznie za pomocą zmieniających się współrzędnych, np.

${\displaystyle {\vec {r}}(q^{1},q^{2},c)}$

przedstawia powierzchnię współrzędnych ${\displaystyle q^{1},q^{2}}$ przy ustalonej wartości współrzędnej ${\displaystyle q^{3}=c.}$

b) Zmieniając wartość ${\displaystyle c}$ współrzędnej ${\displaystyle q^{3},}$ otrzymuje się różne powierzchnie współrzędnych ${\displaystyle q^{1},q^{2}.}$

c) Postępując podobnie dla pozostałych współrzędnych, uzyskuje się wszystkie powierzchnie współrzędnych krzywoliniowych.

d) Przez każdy punkt ${\displaystyle P(a,b,c)}$ przechodzą trzy przecinające się wzajemnie powierzchnie współrzędnych ${\displaystyle {\vec {r}}(q^{1},q^{2},c),}$ ${\displaystyle {\vec {r}}(a,q^{2},q^{3}),}$ ${\displaystyle {\vec {r}}(q^{1},b,q^{3}).}$

Obliczanie bazy wektorów kowariantnych

W każdym punkcie ${\displaystyle {\vec {r}}}$ przestrzeni można zdefiniować trzy wektory kobazowe, prostopadłe do kolejnych powierzchni ${\displaystyle E^{2}}$ o ustalonej wartości jednej z nowych współrzędnych; wektory te oblicza się jako gradienty nowych współrzędnych

${\displaystyle {\vec {g}}^{1}={\text{grad}}\,q^{1}=\left[{\frac {\partial q^{1}}{\partial x^{1}}},{\frac {\partial q^{1}}{\partial x^{2}}},{\frac {\partial q^{1}}{\partial x^{3}}}\right]={\frac {\partial q^{1}}{\partial x^{1}}}{\vec {e}}_{1}+{\frac {\partial q^{1}}{\partial x^{2}}}{\vec {e}}_{2}+{\frac {\partial q^{1}}{\partial x^{3}}}{\vec {e}}_{3},}$

${\displaystyle {\vec {g}}^{2}={\text{grad}}\,q^{2}=\left[{\frac {\partial q^{2}}{\partial x^{1}}},{\frac {\partial q^{2}}{\partial x^{2}}},{\frac {\partial q^{2}}{\partial x^{3}}}\right]={\frac {\partial q^{2}}{\partial x^{1}}}{\vec {e}}_{1}+{\frac {\partial q^{2}}{\partial x^{2}}}{\vec {e}}_{2}+{\frac {\partial q^{2}}{\partial x^{3}}}{\vec {e}}_{3},}$

${\displaystyle {\vec {g}}^{3}={\text{grad}}\,q^{3}=\left[{\frac {\partial q^{3}}{\partial x^{1}}},{\frac {\partial q^{3}}{\partial x^{2}}},{\frac {\partial q^{3}}{\partial x^{3}}}\right]={\frac {\partial q^{3}}{\partial x^{1}}}{\vec {e}}_{1}+{\frac {\partial q^{3}}{\partial x^{2}}}{\vec {e}}_{2}+{\frac {\partial q^{3}}{\partial x^{3}}}{\vec {e}}_{3},}$

gdzie:

${\displaystyle {\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3}}$ – wektory ortonormalne układu współrzędnych kartezjańskich.

Uwaga 1: Wektory kobazy można formalnie otrzymać z wektorów bazy przez zamianę licznika z mianownikiem we wzorach, np. z ${\displaystyle {\vec {g}}_{1}={\frac {\partial {\vec {r}}}{\partial q^{1}}}}$ otrzyma się ${\displaystyle {\vec {g}}^{1}={\frac {\partial q^{1}}{\partial {\vec {r}}}}{:}}$

${\displaystyle {\begin{alignedat}{1}{\vec {g}}_{1}&{}={\frac {\partial {\vec {r}}}{\partial q^{1}}}&{}=\left[{\frac {\partial x^{1}}{\partial q^{1}}},{\frac {\partial x^{2}}{\partial q^{1}}},{\frac {\partial x^{3}}{\partial q^{1}}}\right]={\frac {\partial x^{1}}{\partial q^{1}}}{\vec {e}}_{1}+{\frac {\partial x^{2}}{\partial q^{1}}}{\vec {e}}_{2}+{\frac {\partial x^{3}}{\partial q^{1}}}{\vec {e}}_{3},\\[1ex]{\vec {g}}^{1}&{}={\text{grad}}\,q^{1}&{}=\left[{\frac {\partial q^{1}}{\partial x^{1}}},{\frac {\partial q^{1}}{\partial x^{2}}},{\frac {\partial q^{1}}{\partial x^{3}}}\right]={\frac {\partial q^{1}}{\partial x^{1}}}{\vec {e}}_{1}+{\frac {\partial q^{1}}{\partial x^{2}}}{\vec {e}}_{2}+{\frac {\partial q^{1}}{\partial x^{3}}}{\vec {e}}_{3}.\end{alignedat}}}$

Uwaga 2: Z powyższej własności wynika, że długości wektorów bazy i kobazy są liczbami wzajemnie odwrotnymi. Innymi słowy: współczynniki Lamego dla wektorów bazy są odwrotnościami współczynników dla wektorów kobazy

${\displaystyle h^{1}={\sqrt {{\vec {g}}^{1}\cdot {\vec {g}}^{1}}}={\frac {1}{h_{1}}},}$

${\displaystyle h^{2}={\sqrt {{\vec {g}}^{2}\cdot {\vec {g}}^{2}}}={\frac {1}{h_{2}}},}$

${\displaystyle h^{3}={\sqrt {{\vec {g}}^{3}\cdot {\vec {g}}^{3}}}={\frac {1}{h_{3}}}.}$

Powyższe współczynniki naszą nazwę współczynników Lamego dla wektorów kobazy.

Uwaga 3: Wektory ${\displaystyle {\vec {g}}^{1},{\vec {g}}^{2},{\vec {g}}^{3}}$ kobazy są prostopadłe do powierzchni współrzędnych – wektory te nie są jednak w ogólności ortogonalne, jeśli powierzchnie współrzędnych w danym punkcie nie przecinają się pod kątami prostymi. Ponadto wektory te nie są unormowane do ${\displaystyle 1,}$ co więcej – ich długość może zmieniać się ze zmianą położenia ${\displaystyle {\vec {r}}}$ w przestrzeni.

Przykład: Ortonormalna baza wektorów kowariantnych

Współrzędne sferyczne

(1) Współrzędne sferyczne ${\displaystyle r,\phi ,\theta }$ są wyrażone przez współrzędne kartezjańskie ${\displaystyle x,y,z{:}}$

${\displaystyle r={\sqrt {x^{2}+y^{2}+z^{2}}},}$

${\displaystyle \phi =\mathrm {arctg} {\frac {y}{x}},}$

${\displaystyle \theta =\mathrm {arctg} {\frac {\sqrt {x^{2}+y^{2}}}{z}}.}$

(2) Obliczamy wektory kobazy:

${\displaystyle {\vec {g}}^{r}={\frac {\partial r}{\partial {\vec {r}}}}=\left[{\frac {\partial r}{\partial x}},{\frac {\partial r}{\partial y}},{\frac {\partial r}{\partial z}}\right]=[\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta ],}$

${\displaystyle {\vec {g}}^{\theta }={\frac {\partial \theta }{\partial {\vec {r}}}}=\left[{\frac {\partial \theta }{\partial x}},{\frac {\partial \theta }{\partial y}},{\frac {\partial \theta }{\partial z}}\right]=\left[{\frac {\cos \theta \cos \phi }{r}},{\frac {\cos \theta \sin \phi }{r}},-{\frac {\sin \theta }{r}}\right],}$

${\displaystyle {\vec {g}}^{\phi }={\frac {\partial \phi }{\partial {\vec {r}}}}=\left[{\frac {\partial \phi }{\partial x}},{\frac {\partial \phi }{\partial y}},{\frac {\partial \phi }{\partial z}}\right]=\left[-{\frac {\sin \phi }{r\sin \theta }},{\frac {\cos \phi }{r\sin \theta }},0\right].}$

(3) Wektory te są ortogonalne, gdyż zerują się ich iloczyny skalarne

${\displaystyle {\vec {g}}^{r}\cdot {\vec {g}}^{\theta }=0,\quad {\vec {g}}^{r}\cdot {\vec {g}}^{\phi }=0,\quad {\vec {g}}^{\theta }\cdot {\vec {g}}^{\phi }=0,}$

co łatwo policzyć.

(4) Obliczamy długości wektorów ${\displaystyle {\vec {g}}^{r},{\vec {g}}^{\phi },{\vec {g}}^{\theta },}$ czyli współczynniki Lamego

${\displaystyle h^{r}={\sqrt {{\vec {g}}^{r}\cdot {\vec {g}}^{r}}}={\sqrt {(\sin \theta \cos \phi )^{2}+(\sin \theta \sin \phi )^{2}+(\cos \theta )^{2}}}=1,}$

${\displaystyle h^{\theta }={\sqrt {{\vec {g}}^{\theta }\cdot {\vec {g}}^{\theta }}}={\sqrt {(\dots )^{2}+(\dots )^{2}+(\dots )^{2}}}={\frac {1}{r}},}$

${\displaystyle h^{\phi }={\sqrt {{\vec {g}}^{\phi }\cdot {\vec {g}}^{\phi }}}={\sqrt {(\dots )^{2}+(\dots )^{2}+0^{2}}}={\frac {1}{r\sin \theta }}.}$

Porównując współczynniki Lamego dla bazy ze współczynnikami dla kobazy, widać, że są one parami, liczbami wzajemnie odwrotnymi, tj. ${\displaystyle h^{r}=1/{h_{r}},\ h^{\theta }=1/{h_{\theta }},\ h^{\phi }=1/{h_{\phi }}.}$

(5) Normujemy wektory ${\displaystyle {\vec {g}}_{r},{\vec {g}}_{\theta },{\vec {g}}_{\phi }}$ do ${\displaystyle 1,}$ dzieląc je przez ich długości

${\displaystyle {\hat {g}}^{r}={\frac {{\vec {g}}^{r}}{h^{r}}}=[\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta ],}$

${\displaystyle {\hat {g}}^{\theta }={\frac {{\vec {g}}^{\theta }}{h^{\theta }}}=[\cos \theta \cos \phi ,\cos \theta \sin \phi ,-\sin \theta ],}$

${\displaystyle {\hat {g}}^{\phi }={\frac {{\vec {g}}^{\phi }}{h^{\phi }}}=[-\sin \phi ,\cos \phi ,0].}$

Powyższe wektory tworzą kobazę ortonormalną układu współrzędnych sferycznych. Widać, że współrzędne tych wektorów zależą tylko od współrzędnych ${\displaystyle \phi ,\theta }$ punktu ${\displaystyle {\vec {r}}=(r\,\phi ,\theta ),}$ w którym te wektory obliczono.

(6) Porównując wektory kobazy ortonormalnej ${\displaystyle {\hat {g}}^{r},{\hat {g}}^{\theta },{\hat {g}}^{\phi }}$ z wektorami bazy ortonormalnej ${\displaystyle {\hat {g}}_{r},{\hat {g}}_{\theta },{\hat {g}}_{\phi },}$ widać, że są one parami identyczne. Oznacza to, że wektory nieunormowane ${\displaystyle {\vec {g}}^{r},{\vec {g}}^{\phi },{\vec {g}}^{\theta }}$ oraz ${\displaystyle {\vec {g}}_{r},{\vec {g}}_{\phi },{\vec {g}}_{\theta }}$ są parami do siebie równoległe.

Jest to przejawem ogólnej własności: wektory bazy i kobazy dla współrzędnych krzywoliniowych ortogonalnych są parami równoległe.

Tensor metryczny

Niezmiennik infinitezymalnego przemieszczenia

Wyrażając w bazie ${\displaystyle {\vec {g}}_{i},\;i=1,2,3}$ układu współrzędnych wektor infinitezymalnego przemieszczenia ${\displaystyle d{\vec {r}}}$ (tj. ${\displaystyle d{\vec {r}}=dq^{i}{\vec {g}}_{i}),}$ otrzyma się wielkość skalarną

${\displaystyle ds^{2}\equiv |d{\vec {r}}|^{2}=d{\vec {r}}\cdot d{\vec {r}}=dq^{i}{\vec {g}}_{i}\cdot dq^{j}{\vec {g}}_{j}={\vec {g}}_{i}{\cdot }{\vec {g}}_{j}\,dq^{i}dq^{j}.}$

Można pokazać, że powyższa wielkość jest niezmiennikiem, co jest zgodne z tym, iż iloczyn skalarny wektorów jest wielkością geometryczną, niezależną od bazy, w której wektory się wyraża.

Iloczyny skalarne wektorów bazy ${\displaystyle {\vec {g}}_{i}\cdot {\vec {g}}_{j}}$ mają istotne znaczenie – tworzą tensor metryczny (kowariantny).

Definicja tensora metrycznego

1) Tensorem metrycznym kowariantnym nazywa się tensor ${\displaystyle g_{ij}}$ utworzony z iloczynów skalarnych wektorów bazy, tj.

${\displaystyle g_{ij}={\vec {g}}_{i}{\vec {g}}_{j}.}$

2) Tensorem metrycznym kontrawariantnym nazywa się tensor utworzony z iloczynów skalarnych wektorów kobazy, tj.

${\displaystyle g^{ij}={\vec {g}}^{i}{\vec {g}}^{j}.}$

3) Tensorem metrycznym mieszanym nazywa się tensor

${\displaystyle g_{i}^{\,\,j}={\vec {g}}_{i}\,{\vec {g}}^{j}=\delta _{i}^{\,j}}$

lub

${\displaystyle g_{\,j}^{i}={\vec {g}}^{i}\,{\vec {g}}_{j}=\delta _{j}^{i}.}$

Wyrażenie tensora metrycznego przez współrzędne krzywoliniowe

Zapisując wektory ${\displaystyle {\vec {g}}_{i},{\vec {g}}_{j},{\vec {g}}^{i},{\vec {g}}^{j}}$ w bazie kartezjańskiej przestrzeni euklidesowej, takiej że ${\displaystyle {\vec {e}}_{i}\,{\vec {e}}_{j}=\delta _{ij},}$ otrzyma się jawne postacie tensora metrycznego:

${\displaystyle g_{ij}={\vec {g}}_{i}{\vec {g}}_{j}={\frac {\partial x^{k}}{\partial q^{i}}}{\vec {e}}_{k}{\frac {\partial x^{l}}{\partial q^{j}}}{\vec {e}}_{l}={\frac {\partial x^{k}}{\partial q^{i}}}{\frac {\partial x^{l}}{\partial q^{j}}}\delta _{kl}=\sum _{k}{\frac {\partial x^{k}}{\partial q^{i}}}{\frac {\partial x^{k}}{\partial q^{j}}},}$

${\displaystyle g^{ij}={\vec {g}}^{i}{\vec {g}}^{j}={\frac {\partial q^{i}}{\partial x^{k}}}{\vec {e}}_{k}{\frac {\partial q^{j}}{\partial x^{l}}}{\vec {e}}_{l}={\frac {\partial q^{i}}{\partial x^{k}}}{\frac {\partial q^{j}}{\partial x^{l}}}\delta _{kl}=\sum _{k}{\frac {\partial q^{i}}{\partial x^{k}}}{\frac {\partial q^{j}}{\partial x^{k}}},}$

${\displaystyle g_{i}^{\,\,j}={\vec {g}}_{i}\,{\vec {g}}^{j}={\frac {\partial x^{k}}{\partial q^{i}}}{\vec {e}}_{k}{\frac {\partial q^{j}}{\partial x^{l}}}{\vec {e}}_{l}={\frac {\partial x^{k}}{\partial q^{i}}}{\frac {\partial q^{j}}{\partial x^{l}}}\delta _{k}^{l}={\frac {\partial x^{k}}{\partial q^{i}}}{\frac {\partial q^{j}}{\partial x^{k}}}={\frac {\partial q^{j}}{\partial q^{i}}}=\delta _{i}^{j}.}$

Ostatni wynik oznacza, że tensor metryczny mieszany jest reprezentowany przez macierz jednostkową.

Uwaga: Założenie, że iloczyny skalarne wersorów bazy mają postać ${\displaystyle {\vec {e}}_{i}\,{\vec {e}}_{j}=\delta _{ij}}$ jest charakterystyczne dla przestrzeni euklidesowych. Zadanie innej postaci tych fundamentalnych relacji definiuje inne możliwe geometrie (patrz dalej).

Wyznacznik tensora metrycznego

Wyznacznik tensora metrycznego kowariantnego oznacza się symbolem

${\displaystyle g=\det(g_{ij}).}$

Przykłady

(1) Układ kartezjański

Wektory bazy są ortonormalne – tensor metryczny ma postacie

${\displaystyle g_{ij}={\vec {e}}_{i}{\vec {e}}_{j}=\delta _{ij},}$

${\displaystyle g^{ij}={\vec {e}}^{i}{\vec {e}}^{j}=\delta ^{ij},}$

${\displaystyle g_{j}^{i}={\vec {e}}^{i}{\vec {e}}_{j}=\delta _{j}^{i}.}$

W reprezentacji macierzowej mamy

${\displaystyle g_{ij}=g^{ij}=g_{\,j}^{i}=g_{i}^{\,j}={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}}$

oraz ${\displaystyle g=\det(g_{ij})=1.}$

(2) Układ sferyczny

A. Elementy tensora metrycznego kowariantnego otrzyma się, licząc iloczyny skalarne wektorów bazy (postacie wektorów bazy układu sferycznego – patrz wyżej), tj.

${\displaystyle {\begin{array}{l}g_{11}={\vec {e}}_{r}{\vec {e}}_{r}=1,&g_{12}={\vec {e}}_{r}{\vec {e}}_{\theta }=0,&g_{13}={\vec {e}}_{r}{\vec {e}}_{\phi }=0,\\g_{21}={\vec {e}}_{\theta }{\vec {e}}_{r}=0,&g_{22}={\vec {e}}_{\theta }{\vec {e}}_{\theta }=r^{2},&g_{23}={\vec {e}}_{\theta }{\vec {e}}_{\phi }=0,\\g_{31}={\vec {e}}_{\phi }{\vec {e}}_{r}=0,&g_{32}={\vec {e}}_{\phi }{\vec {e}}_{\theta }=0,&g_{33}={\vec {e}}_{\phi }{\vec {e}}_{\phi }=r^{2}\sin ^{2}(\theta ).\end{array}}}$

W reprezentacji macierzowej mamy

${\displaystyle g_{ij}={\begin{pmatrix}1&0&0\\0&r^{2}&0\\0&0&r^{2}\sin ^{2}\theta \end{pmatrix}}.}$

Wyznacznik tensora:

${\displaystyle g=\det(g_{ij})=r^{4}\sin ^{2}(\theta ).}$

B. Elementy tensora metrycznego kontrawariantnego otrzyma się, licząc iloczyny skalarne wektorów kobazy (postacie wektorów kobazy układu sferycznego – patrz wyżej), tj.

${\displaystyle g^{11}={\vec {e}}^{r}{\vec {e}}^{r}=1,\quad g^{12}={\vec {e}}^{r}{\vec {e}}^{\theta }=0,\quad g^{13}={\vec {e}}^{r}{\vec {e}}^{\phi }=0}$

itd.

W reprezentacji macierzowej otrzyma się

${\displaystyle g^{ij}={\begin{pmatrix}1&0&0\\0&{\frac {1}{r^{2}}}&0\\0&0&{\frac {1}{r^{2}\sin ^{2}\theta }}\end{pmatrix}}.}$

Wyznacznik tensora:

${\displaystyle \det(g^{ij})={\frac {1}{r^{4}\sin ^{2}(\theta )}}.}$

C. Z powyższego widać, że

${\displaystyle \det(g^{ij})=\det(g_{ij})^{-1}=g^{-1}.}$

Wynika stąd, że iloczyn tensorów ${\displaystyle g^{ij}}$ oraz ${\displaystyle g_{ij}}$ daje macierz jednostkową. Tensory kowariantny i kontrawariantny są więc reprezentowane przez macierze wzajemnie odwrotne, tj.

${\displaystyle [g^{ij}]=[g_{ij}]^{-1}.}$

D. Elementy tensora metrycznego mieszanego otrzyma się, licząc iloczyny skalarne wektorów bazy i kobazy, co daje

${\displaystyle {\begin{array}{l}g_{\,1}^{1}={\vec {e}}^{r}{\vec {e}}_{r}=1,&g_{\,2}^{1}={\vec {e}}^{r}{\vec {e}}_{\theta }=0,&g_{\,3}^{1}={\vec {e}}^{r}{\vec {e}}_{\phi }=0,\\g_{\,\,1}^{2}={\vec {e}}^{\theta }{\vec {e}}_{r}=0,&g_{\,\,2}^{2}={\vec {e}}^{\theta }{\vec {e}}_{\theta }=1,&g_{\,\,3}^{2}={\vec {e}}^{\theta }{\vec {e}}_{\phi }=0,\\g_{\,\,1}^{3}={\vec {e}}^{\phi }{\vec {e}}_{r}=0,&g_{\,\,2}^{3}={\vec {e}}^{\phi }{\vec {e}}_{\theta }=0,&g_{\,\,3}^{3}={\vec {e}}^{\phi }{\vec {e}}_{\phi }=1.\end{array}}}$

Tensor metryczny mieszany jest więc w reprezentacji macierzowej macierzą jednostkową

${\displaystyle g_{\,j}^{i}={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}.}$

Podnoszenie i opuszczanie wskaźników tensorów

Tensor metryczny pozwala łatwo podnosić i opuszczać wskaźniki wektorów i tensorów, np.

${\displaystyle A_{i}=g_{ij}A^{j},}$

${\displaystyle A^{i}=g^{ij}A_{j},}$

${\displaystyle T_{ij}=g_{ik}\,g_{jl}\,T^{kl},\quad T^{ij}=g^{ik}\,g^{jl}\,T_{kl}.}$

Wzory te realizują transformacje współrzędnych od kowariantnych do kontrawariantnych i odwrotnie.

Pochodna pola wektorowego. Pochodna kowariantna

Pochodna w układzie kartezjańskim

Załóżmy, że zadane jest w przestrzeni pole wektorowe

${\displaystyle {\vec {A}}(x^{1},x^{2},x^{3})=A^{i}(x^{1},x^{2},x^{3}){\vec {e}}_{i},}$

tj.

${\displaystyle {\vec {A}}(x^{1},x^{2},x^{3})=[A^{1}(x^{1},x^{2},x^{3}),A^{2}(x^{1},x^{2},x^{3}),A^{3}(x^{1},x^{2},x^{3})]}$

i rozważmy zagadnienie obliczania pochodnej cząstkowej tego pola względem jednej ze współrzędnych przestrzennych kartezjańskich ${\displaystyle x^{j},\,\,j=1,2,3.}$

Jeżeli pole jest wyrażone w układzie kartezjańskim, to pochodna ta jest wektorem, którego składowe są pochodnymi cząstkowymi współrzędnych pola po współrzędnych kartezjańskich, tj.${\displaystyle {\vec {A}}=[A^{1},A^{2},A^{3}]=A^{i}{\vec {e}}_{i}}$

${\displaystyle {\frac {\partial {\vec {A}}}{\partial x^{j}}}={\frac {\partial (A^{i}{\vec {e}}_{i})}{\partial x^{j}}}={\frac {\partial A^{i}}{\partial x^{j}}}{\vec {e}}_{i}.}$

Dziewięć wielkości

${\displaystyle {\frac {\partial A^{i}}{\partial x^{j}}},\,\,i,j=1,2,3}$

tworzy tensor 2-go rzędu kontrawariantno-kowariantny, który można przedstawić w postaci macierzy

${\displaystyle T_{j}^{i}=\left[{\begin{matrix}{\frac {\partial A^{1}}{\partial x^{1}}}&{\frac {\partial A^{1}}{\partial x^{2}}}&{\frac {\partial A^{1}}{\partial x^{3}}}\\{\frac {\partial A^{2}}{\partial x^{1}}}&{\frac {\partial A^{2}}{\partial x^{2}}}&{\frac {\partial A^{2}}{\partial x^{3}}}\\{\frac {\partial A^{3}}{\partial x^{1}}}&{\frac {\partial A^{3}}{\partial x^{2}}}&{\frac {\partial A^{3}}{\partial x^{3}}}\end{matrix}}\right].}$

Pochodna w układzie krzywoliniowym

W obliczaniach pochodnej pola wektorowego w układzie krzywoliniowym należy uwzględnić fakt, że podczas niewielkiego przesunięcia wektora zmieniają się jego współrzędne na skutek zarówno zmian pola, jak i na skutek zmiany lokalnego układu współrzędnych (który jest „przyczepiony” w nieco innym punkcie przecięcia krzywych współrzędnych). W wyniku tego pochodna funkcji wektorowej we współrzędnych krzywoliniowych wyraża się nieco innym wzorem niż w układzie kartezjańskim.

(1) Mianowicie, licząc pochodną mamy:

${\displaystyle {\frac {\partial {\vec {A}}}{\partial q^{j}}}={\frac {\partial (A^{i}{\vec {g}}_{i})}{\partial q^{j}}}={\frac {\partial A^{i}}{\partial q^{j}}}{\vec {g}}_{i}+A^{i}{\frac {\partial {\vec {g}}_{i}}{\partial q^{j}}}.}$

(2) Ponieważ ${\displaystyle {\vec {g}}_{i}={\frac {\partial {\vec {r}}}{\partial q^{i}}},}$ to

${\displaystyle {\frac {\partial {\vec {g}}_{i}}{\partial q^{j}}}={\frac {\partial }{\partial q^{j}}}\left({\frac {\partial {\vec {r}}}{\partial q^{i}}}\right)={\frac {\partial }{\partial q^{j}}}\left({\frac {\partial x^{l}}{\partial q^{i}}}{\vec {e}}_{l}\right)=\left({\frac {\partial ^{2}x^{l}}{\partial q^{i}\partial q^{j}}}\right){\vec {e}}_{l}.}$

Wektor ${\displaystyle {\vec {e}}_{l}}$ wyraża się za pomocą wektorów ${\displaystyle {\vec {g}}_{k}}$ zależnością

${\displaystyle {\vec {e}}_{l}={\frac {\partial q^{k}}{\partial x^{l}}}{\vec {g}}_{k}.}$

Stąd otrzymuje się

${\displaystyle {\frac {\partial {\vec {g}}_{i}}{\partial q^{j}}}=\left({\frac {\partial ^{2}x^{l}}{\partial q^{i}\partial q^{j}}}\right){\frac {\partial q^{k}}{\partial x^{l}}}{\vec {g}}_{k}=\Gamma _{ij}^{k}\,{\vec {g}}_{k},}$

po wprowadzeniu symbolu Christoffela II rodzaju

${\displaystyle \Gamma _{ij}^{k}={\frac {\partial ^{2}x^{l}}{\partial q^{i}\partial q^{j}}}{\frac {\partial q^{k}}{\partial x^{l}}}.}$

(3) Wstawiając powyższy wynik do wzoru z punktu (1), mamy

${\displaystyle {\frac {\partial {\vec {A}}}{\partial q^{j}}}={\frac {\partial A^{i}}{\partial q^{j}}}{\vec {g}}_{i}+A^{i}\Gamma _{ij}^{k}\,{\vec {g}}_{k}.}$

Zmieniając nazwy indeksów, ostatecznie otrzymujemy

${\displaystyle {\frac {\partial {\vec {A}}}{\partial q^{j}}}=\left({\frac {\partial A^{i}}{\partial q^{j}}}+A^{k}\Gamma _{kj}^{i}\right){\vec {g}}_{i}.}$

Wyrażenie w nawiasie nazywa się pochodną kowariantną współrzędnej ${\displaystyle A^{i}}$ wektora ${\displaystyle {\vec {A}}}$ po współrzędnej ${\displaystyle q^{j},}$ tj.

${\displaystyle A_{;\,j}^{i}={\frac {\partial A^{i}}{\partial q^{j}}}+A^{k}\Gamma _{kj}^{i}.}$

Uwaga: Znak średnika wraz z indeksem umieszczony u dołu oznacza pochodną kowariantną po współrzędnej przestrzennej o tym indeksie.

(4) Analogiczne rozumowanie prowadzi do wyrażenia na pochodną kowariantną wektora kowariantnego

${\displaystyle A_{i;\,j}={\frac {\partial A_{i}}{\partial q^{j}}}-A_{k}\Gamma _{ij}^{k}.}$

(5) Pochodne kowariantne wektorów są tensorami 2-go rzędu. W przestrzeni 3-wymiarowej mają 9 składowych. W układzie kartezjańskim symbole Christoffela zerują się – pochodne kowariantne stają się równe pochodnym cząstkowym.

(6) Wektor ${\displaystyle D{\vec {A}}=DA^{i}{\vec {g}}_{i}=DA_{i}{\vec {g}}^{i}}$ infinitezymalnej zmiany pola wektorowego w wyniku infinitezymalnego przemieszczenia ${\displaystyle dq^{j}}$ ma współrzędne kontra- i kowariantne w postaci:

${\displaystyle DA^{i}=A_{\,\,;\,j}^{i}dq^{j}=\left({\frac {\partial A^{i}}{\partial q^{j}}}+A^{k}\Gamma _{kj}^{i}\right)dq^{j}}$

oraz

${\displaystyle DA_{i}=A_{i;\,j}dq^{j}=\left({\frac {\partial A_{i}}{\partial q^{j}}}-A_{k}\Gamma _{ij}^{k}\right)dq^{j}.}$

Element różniczkowy objętości

W układzie kartezjańskim element różniczkowy objętości ma postać

${\displaystyle dV=dx^{1}\,dx^{2}\,dx^{3}.}$

Po przejściu do dowolnego układu współrzędnych krzywoliniowych ${\displaystyle q^{1},\,q^{2},\,q^{3},}$ różniczkowy element objętości wyraża się wzorem

${\displaystyle dV=|\det \,\mathbf {J} |\ dq^{1}\,dq^{2}\,dq^{3},}$

gdzie:

${\displaystyle \mathbf {J} =\left[{\frac {\partial x^{i}}{\partial q^{\alpha }}}\right]}$ – macierz Jacobiego transformacji współrzędnych.

Macierz Jacobiego można wyrazić za pomocą elementów tensora metrycznego: kwadrat jakobianu jest równy wyznacznikowi tensora metrycznego, tj.

${\displaystyle g\equiv \det \,g_{\alpha \beta }=\left|{\frac {\partial x^{i}}{\partial q^{\alpha }}}\right|^{2}.}$

Stąd element objętości w dowolnym układzie współrzędnych ma postać

${\displaystyle dV={\sqrt {g}}\;dq^{1}\ dq^{2}\ dq^{3}.}$

Przykład: Różniczkowy element objętości

W układzie współrzędnych sferycznych ${\displaystyle q^{1}=r,q^{2}=\theta ,q^{3}=\phi }$ mamy ${\displaystyle g=\det(g_{ij})=r^{4}\sin ^{2}(\theta ).}$ Stąd otrzymamy:

${\displaystyle dV={\sqrt {g}}\;dq^{1}\,dq^{2}\,dq^{3}=r^{2}\sin(\theta )\,dr\,d\theta \,d\phi .}$

Zasady transformacji współrzędnych obiektów geometrycznych

Transformacja różniczek współrzędnych

(1) Załóżmy, że nieznacznie zmieniamy położenie w przestrzeni z położenia ${\displaystyle {\vec {r}}_{A}(x^{1},x^{2},x^{3})}$ do położenia ${\displaystyle {\vec {r}}_{B}(x^{1}+dx^{1},x^{2}+dx^{2},x^{3}+dx^{3}).}$ Wielkości ${\displaystyle dx^{1},dx^{2},dx^{3}}$ nazywa się różniczkami współrzędnych kartezjańskich.

Jeżeli wektory ${\displaystyle {\vec {r}}_{A}}$ oraz ${\displaystyle {\vec {r}}_{B}}$ zapisze się we współrzędnych krzywoliniowych, to otrzymamy wektory ${\displaystyle {\vec {r}}_{A}(q^{1},q^{2},q^{3})}$ oraz ${\displaystyle {\vec {r}}_{B}(q^{1}+dq^{1},q^{2}+dq^{2},q^{3}+dq^{3}),}$ gdzie ${\displaystyle dq^{1},dq^{2},dq^{3}}$ – różniczki zmian współrzędnych krzywoliniowych. Różniczki te tworzą wektor infinitezymalnego przemieszczenia

${\displaystyle d{\vec {r}}=dq^{i}{\vec {g}}_{i}=dx^{i}{\vec {e}}_{i}.}$

(2) Związki między różniczkami ${\displaystyle dx^{1},dx^{2},dx^{3}}$ oraz ${\displaystyle dq^{1},dq^{2},dq^{3}}$ można znaleźć, obliczając różniczki zupełne współrzędnych ${\displaystyle x^{i}(q^{1},q^{2},q^{3}),\;i=1,2,3}$ wyrażonych przez współrzędne krzywoliniowe

${\displaystyle dx^{1}={\frac {\partial x^{1}}{\partial q^{1}}}dq^{1}+{\frac {\partial x^{1}}{\partial q^{2}}}dq^{2}+{\frac {\partial x^{1}}{\partial q^{3}}}dq^{3},}$

${\displaystyle dx^{2}={\frac {\partial x^{2}}{\partial q^{1}}}dq^{1}+{\frac {\partial x^{2}}{\partial q^{2}}}dq^{2}+{\frac {\partial x^{2}}{\partial q^{3}}}dq^{3},}$

${\displaystyle dx^{3}={\frac {\partial x^{3}}{\partial q^{1}}}dq^{1}+{\frac {\partial x^{3}}{\partial q^{2}}}dq^{2}+{\frac {\partial x^{3}}{\partial q^{3}}}dq^{3}.}$

lub w skrócie, stosując konwencję sumacyjną po powtarzającym się wskaźniku ${\displaystyle \alpha }$

${\displaystyle dx^{i}={\frac {\partial x^{i}}{\partial q^{\alpha }}}dq^{\alpha },\quad i=1,2,3.}$

Odwracając tę zależność, otrzyma się wzór na transformację różniczek ${\displaystyle dx^{i},\;i=1,2,3}$ współrzędnych kartezjańskich ${\displaystyle x^{1},x^{2},x^{3}}$ w różniczki ${\displaystyle dq^{\alpha },\alpha =1,2,3}$ współrzędnych krzywoliniowych ${\displaystyle q^{1},q^{2},q^{3}}$

${\displaystyle dq^{\alpha }={\frac {\color {red}\partial q^{\alpha }}{\color {green}\partial x^{i}}}{dx^{i}}.}$

Oznacza to, że:

Różniczki ${\displaystyle dx^{i}}$ współrzędnych kartezjańskich transformują się na różniczki ${\displaystyle dq^{\alpha }}$ współrzędnych krzywoliniowych za pomocą macierzy ${\displaystyle \Lambda _{i}^{\alpha }=\left[{\frac {\partial q^{\alpha }}{\partial x^{i}}}\right],}$ która jest odwrotna do macierzy ${\displaystyle \Lambda _{\alpha }^{i}=\left[{\frac {\partial x^{i}}{\partial q^{\alpha }}}\right]}$ transformacji wektorów bazy ${\displaystyle {\vec {e}}_{i}}$ na wektory bazy ${\displaystyle {\vec {g}}_{\alpha }.}$

Wektory, które transformują się tak jak wektory infinitezymalnego przemieszczenia ${\displaystyle d{\vec {r}}}$ (lub inaczej mówiąc: jak różniczki współrzędnych) nazywa się wektorami kontrawariantnymi.

Nazwa kontrawariantny oznacza: przeciwny w sposobie transformacji niż wektory bazy.

Transformacja współrzędnych gradientu funkcji

(1) Niech dana będzie funkcja skalarna współrzędnych ${\displaystyle F(x^{1},x^{2},x^{3})\colon E^{3}\to R.}$ Gradient funkcji skalarnej – to wektor, który we współrzędnych kartezjańskich dany jest wzorem

${\displaystyle {\text{grad}}\,F=\left[{\frac {\partial F}{\partial x^{1}}},{\frac {\partial F}{\partial x^{2}}},{\frac {\partial F}{\partial x^{3}}}\right]={\frac {\partial F}{\partial x^{1}}}{\vec {e}}_{1}+{\frac {\partial F}{\partial x^{2}}}{\vec {e}}_{2}+{\frac {\partial F}{\partial x^{3}}}{\vec {e}}_{3},}$

tzn. ${\displaystyle i}$-te współrzędne kartezjańskie gradientu są równe pochodnym cząstkowym funkcji po zmiennej ${\displaystyle x^{i}.}$

(2) Współrzędne gradientu wyrażonego we współrzędnych krzywoliniowych.

Jeżeli zapisze się funkcję ${\displaystyle F}$ za pomocą współrzędnych krzywoliniowych, to obliczenie gradientu nie będzie wyrażać się takim samym wzorem jak wyżej. Np. pierwsza składowa gradientu zapisana za pomocą współrzędnych krzywoliniowych ma postać

${\displaystyle {\frac {\partial F}{\partial x^{1}}}={\frac {\partial F}{\partial q^{1}}}{\frac {\partial q^{1}}{\partial x^{1}}}+{\frac {\partial F}{\partial q^{2}}}{\frac {\partial q^{2}}{\partial x^{1}}}+{\frac {\partial F}{\partial q^{3}}}{\frac {\partial q^{3}}{\partial x^{1}}}}$

i analogicznie pozostałe składowe; w skróconym zapisie mamy

${\displaystyle {\frac {\partial F}{\partial x^{i}}}={\frac {\partial F}{\partial q^{\alpha }}}{\frac {\partial q^{\alpha }}{\partial x^{i}}},\quad i=1,2,3,}$

co po odwróceniu daje

${\displaystyle {\frac {\partial F}{\partial q^{\alpha }}}={\frac {\partial x^{i}}{\partial q^{\alpha }}}{\frac {\partial F}{\partial x^{i}}},\quad \alpha =1,2,3.}$

Oznacza to, że:

Współrzędne kartezjańskie ${\displaystyle {\frac {\partial F}{\partial x_{i}}}}$ gradientu transformują się na współrzędne krzywoliniowe ${\displaystyle {\frac {\partial F}{\partial q_{\alpha }}}}$ gradientu za pomocą macierzy ${\displaystyle \Lambda _{\alpha }^{i}=\left[{\frac {\partial x^{i}}{\partial q^{\alpha }}}\right]}$ identycznej jak macierz transformacji wektorów bazy ${\displaystyle {\vec {e}}_{i}}$ na wektory bazy ${\displaystyle {\vec {g}}_{\alpha }.}$

Wektory, które transformują się tak jak gradient, nazywa się wektorami kowariantnymi.

Nazwa kowariantny oznacza: zgodny w sposobie transformacji z wektorami bazy.

Uwaga:

Gradient funkcji skalarnej jest wektorem kowariantnym; zgodne z przyjętą konwencją możemy napisać

${\displaystyle A_{i}={\frac {\partial F}{\partial x^{i}}},\quad i=1,2,3}$

oraz

${\displaystyle A_{\alpha }={\frac {\partial F}{\partial q^{\alpha }}},\quad \alpha =1,2,3.}$

Oznacza to, że

Pochodne funkcji skalarnej po współrzędnych kartezjańskich lub dowolnych współrzędnych krzywoliniowych są współrzędnymi kowariantnymi pewnego wektora.

Definicja transformacyjna tensorów kowariantnych i kontrawariantnych

Powyższe wzory na transformację różniczek współrzędnych i składowych gradientu funkcji określają dwa sposoby transformacji składowych dowolnych obiektów geometrycznych (skalarów, wektorów, tensorów wyższych rzędów) przy zmianie układu współrzędnych.

Definicja

(1) Składowymi kowariantnymi wektorów, tensorów 2-go rzędu itd. nazywa się te ich współrzędne, które transformują poprzez macierz ${\displaystyle \Lambda _{\alpha }^{i}=\left[{\frac {\partial x^{i}}{\partial q^{\alpha }}}\right],}$ tj. identyczną z macierzą transformacji bazy układu kartezjańskiego do bazy układu krzywoliniowego (mówi się, że składowe kowariantne transformują się współzmienniczo lub ko-wariantnie z wektorami bazy).

(2) Składowymi kontrawariantnymi wektorów, tensorów nazywa się te ich współrzędne, które transformują się poprzez macierz odwrotną ${\displaystyle \Lambda _{i}^{\alpha }=\left[{\frac {\partial q^{\alpha }}{\partial x^{i}}}\right]}$ (transformują się przeciwzmienniczo lub kontra-wariantnie).

Wektor położenia nie jest tensorem 1-go rzędu

(1) W myśl powyższej definicji – zwanej definicją transformacyjną – wielkość ${\displaystyle {\vec {r}}=x^{i}{\vec {e}}_{i}}$ nie jest wektorem, gdyż transformuje się w ${\displaystyle {\vec {r}}=q^{i}{\vec {g}}_{i}}$ za pomocą funkcji ${\displaystyle x^{i}=x^{i}(q^{1},q^{2},q^{3}),\;i=1,2,3,}$ a nie za pomocą macierzy ${\displaystyle \Lambda _{i}^{\alpha }=\left[{\frac {\partial q^{\alpha }}{\partial x^{i}}}\right]}$ czy macierzy odwrotnej.

(2) Wynika stąd, iż definicja transformacyjna eliminuje ze zbioru tensorów 1-go rzędu (zwanych wektorami) wielkości, które zależą od wyboru punktu początkowego układu współrzędnych. Wektorami są wielkości, których własności transformacyjne są określone lokalnie, w miejscu gdzie dany wektor jest przyczepiony.

Gradient we współrzędnych krzywoliniowych

Wzór na gradient funkcji skalarnej ${\displaystyle F}$

Wychodząc z definicji gradientu, mamy

${\displaystyle {\frac {\partial F}{\partial {\vec {r}}}}=\left[{\frac {\partial F}{\partial x}},{\frac {\partial F}{\partial y}},{\frac {\partial F}{\partial z}}\right]=\left[{\frac {\partial F}{\partial q_{\alpha }}}{\frac {\partial q_{\alpha }}{\partial x}},{\frac {\partial F}{\partial q_{\alpha }}}{\frac {\partial q_{\alpha }}{\partial y}},{\frac {\partial F}{\partial q_{\alpha }}}{\frac {\partial q_{\alpha }}{\partial z}}\right].}$

Po wyciągnięci tego samego czynnika przed nawias otrzymamy

${\displaystyle {\frac {\partial F}{\partial {\vec {r}}}}={\frac {\partial F}{\partial q_{\alpha }}}\left[{\frac {\partial q_{\alpha }}{\partial x}},{\frac {\partial q_{\alpha }}{\partial y}},{\frac {\partial q_{\alpha }}{\partial z}}\right]={\frac {\partial F}{\partial q_{\alpha }}}{\frac {\partial q_{\alpha }}{\partial {\vec {r}}}}={\frac {\partial F}{\partial q_{\alpha }}}{\vec {g}}^{\alpha },}$

przy czym ostatni wyraz jest wektorem kobazy ${\displaystyle {\vec {g}}^{\alpha }={\frac {\partial q_{\alpha }}{\partial {\vec {r}}}}.}$

Czyli gradient wyrażony we współrzędnych krzywoliniowych ma postać:

${\displaystyle {\frac {\partial F}{\partial {\vec {r}}}}={\frac {\partial F}{\partial q_{\alpha }}}{\vec {g}}^{\alpha }.}$

Powyższa postać gradientu jest identyczna jak we współrzędnych kartezjańskich: jest to suma pochodnych funkcji skalarnej po współrzędnych mnożona przez wektor bazy tego układu. Podana metoda obliczania ma więc charakter uniwersalny – dotyczy bowiem dowolnego układu współrzędnych.

Przy tym należy pamiętać, że wektory bazy nie są na ogół ani unormowane ani ortogonalne.

Przykład: Gradient we współrzędnych sferycznych

Dla układu współrzędnych sferycznych mamy

${\displaystyle {\frac {\partial V}{\partial {\vec {r}}}}={\frac {\partial V}{\partial q_{\alpha }}}{\vec {g}}^{\alpha }={\frac {\partial V}{\partial r}}{\vec {g}}^{r}+{\frac {\partial V}{\partial \phi }}{\vec {g}}^{\phi }+{\frac {\partial V}{\partial \theta }}{\vec {g}}^{\theta }.}$

Niech funkcja skalarna ma postać potencjału pola elektrostatycznego wytwarzanego przez ładunek punktowy, tj.

${\displaystyle V(r,\phi ,\theta )={\frac {c}{r}},}$

gdzie ${\displaystyle c}$ – stała liczba. Ponieważ funkcja ${\displaystyle V}$ nie zależy tu of ${\displaystyle \phi ,\theta ,}$ to ostatnie dwa wyrazy zerują się. Otrzymamy więc:

${\displaystyle {\frac {\partial V}{\partial {\vec {r}}}}={\frac {\partial V}{\partial r}}{\vec {g}}^{r}.}$

Pochodna funkcji po r wynosi

${\displaystyle {\frac {\partial V}{\partial r}}=-{\frac {c}{r^{2}}},}$

zaś wektor

${\displaystyle {\vec {g}}^{r}={\frac {\partial r}{\partial {\vec {r}}}}=[\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta ]={\frac {\vec {r}}{r}}.}$

Stąd otrzymamy ostatecznie

${\displaystyle {\frac {\partial V}{\partial {\vec {r}}}}=-{\frac {c}{r^{2}}}{\frac {\vec {r}}{r}}.}$

Widać, że gradient pola skalarnego o symetrii sferycznej jest skierowany radialnie, wzdłuż wektorów ${\displaystyle {\vec {r}}.}$ Przedstawia on siłę natężenie pola elektrostatycznego.

Uogólnienia

Przestrzenie riemannowskie i pseudoriemannowskie

Formalizm opisany tutaj uogólnia się na:

• przestrzenie pseudoeklidesowe, jak przestrzeń Minkowskiego opisująca własności geometryczne 4-wymiarowej czasoprzestrzeni pojawiającej się w Einsteinowskiej szczególnej teorii względności,
• rozmaitości różniczkowe, w tym:

• rozmaitości riemannowskie
• rozmaitości pseudoriemannowskie (m.in. pojawiające się w ogólnej teorii względności Einsteina, gdzie przestrzeń na skutek obecności materii i pół fizycznych zmienia własności geometryczne i z płaskiej staje się zakrzywiona).

Tensor metryczny przestrzeni pseudoeuklidesowych

Składowe tensora metrycznego wyprowadzono (patrz wyżej) w oparciu o założenie, iż iloczyn skalarny wektorów w bazie kartezjańskiej ma postać ${\displaystyle {\vec {e}}_{i}\,{\vec {e}}_{j}=\delta _{ij}.}$ Jest to słuszne dla przestrzeni euklidesowej.

W przestrzeniach pseudoeuklidesowych – do jakich należy np. 4-wymiarowa czasoprzestrzeń szczególnej i ogólnej teorii względności iloczyny skalarne wektorów bazy są zarówno dodatnie, jak i ujemne (ściślej mówiąc: w czasoprzestrzeni definiuje się iloczyny pseudoskalarne wektorów, które nie zawsze są liczbami nieujemnymi). Np. niezmiennik infinitezymalnego przemieszczenia ma w płaskiej czasoprzestrzeni postać

${\displaystyle ds^{2}\equiv |d{\vec {r}}|^{2}=d{\vec {r}}\cdot d{\vec {r}}=c\,dt^{2}-dx^{2}-dy^{2}-dz^{2},}$

co oznacza, że tensor metryczny ma postać

${\displaystyle g_{ij}={\begin{pmatrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}}.}$

Stąd wynika fundamentalne znaczenie elementu ${\displaystyle ds^{2}}$ dla określenia własności geometrii w danej przestrzeni. Ponieważ

${\displaystyle g_{ij}={\vec {e}}_{i}{\vec {e}}_{j},}$

to na podstawie tensora metrycznego widać, że

${\displaystyle {\vec {e}}_{0}{\vec {e}}_{0}=1,}$

ale

${\displaystyle {\vec {e}}_{1}{\vec {e}}_{1}={\vec {e}}_{2}{\vec {e}}_{2}={\vec {e}}_{3}{\vec {e}}_{3}=-1,}$

co oznacza, że długości wektorów bazowych w przestrzeni pseudoeuklidesowej są ujemne (!) (z tego względu, że tradycyjnie przez długość rozumie się wielkości nieujemne, mówi się tu raczej o pseudodługościach wektorów niż o długościach).

Zobacz też

Pojęcia podstawowe

• pochodna kowariantna
• symbole Christoffela
• tensor
• tensor metryczny

Inne

• niezmiennik relatywistyczny
• wektor styczny do krzywej i powierzchni

Przypisy

1. Trajdos 1993 ↓, s. 314–320.
2. Trajdos 1993 ↓, s. 315.

Bibliografia

• T. Trajdos: Matematyka część III. Warszawa: PWN, 1993. ISBN 83-204-1547-0.

Literatura dodatkowa

• L.D. Landau, E.M. Lifszyc: Teoria pola. Warszawa: PWN, 2009.
• P.K. Raszewski: Geometria Riemanna i analiza tensorowa. Warszawa: PWN, 1958.
• J.L. Synge: Rachunek tensorowy. Warszawa: Państwowe Wydawnictwo Naukowe, 1964.

Linki zewnętrzne

• Wprowadzenie do współrzędnych krzywoliniowych film
• Idea wektorów bazowych film – j. ang.

Kontrola autorytatywna (układ współrzędnych):

• LCCN: sh85032236
• GND: 4165813-9
• J9U: 987007562866305171