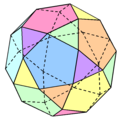
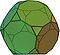
Wielościan półforemny

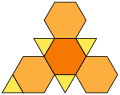
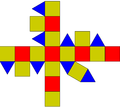
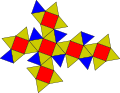
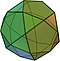
Wielościan półforemny, wielościan archimedesowy^[1] – wielościan spełniający co najmniej trzy warunki:

• jego ściany są foremne;
• w każdym wierzchołku zbiega się jednakowa liczba ścian;
• istnieje izometria przekształcająca każdy wierzchołek na każdy inny (warunek wierzchołkowej tranzytywności)^[2][a].

Jest to uogólnienie wielościanów foremnych (brył platońskich) – wielościany archimedesowe nie mają warunku przystawania ścian. Czasem definiuje się je wężej, wykluczając z nich bryły platońskie^{[potrzebny przypis]}.

Istnieje 13 wielościanów półforemnych (15 jeśli liczyć odbicia lustrzane dwóch spośród nich) oraz dwie nieskończone serie.

Nazwa pochodzi od imienia Archimedesa z Syrakuz^{[potrzebny przypis]}.

Nieskończone serie

• graniastosłupy archimedesowe
• antygraniastosłupy

Pozostałe wielościany półforemne

Nazwa (Konfiguracja wektorowa)	Grafika przejrzysta	Grafika nieprzejrzysta	Siatka	Ściany		Krawędzie	Wierzchołki	Grupa symetryczna
Czworościan ścięty (3.6.6)				8	4 trójkąty 4 sześciokąty	18	12	Td
Sześcio-ośmiościan (3.4.3.4)				14	8 trójkątów 6 kwadratów	24	12	Oh
Sześcian ścięty (3.8.8)				14	8 trójkątów 6 ośmiokątów	36	24	Oh
Ośmiościan ścięty (4.6.6)				14	6 kwadratów 8 sześciokątów	36	24	Oh
Sześcio-ośmiościan rombowy mały (3.4.4.4)				26	8 trójkątów 18 kwadratów	48	24	Oh
Sześcio-ośmiościan rombowy wielki (4.6.8)				26	12 kwadratów 8 sześciokątów 6 ośmiokątów	72	48	Oh
Sześcio-ośmiościan przycięty (3.3.3.3.4)				38	32 trójkąty 6 kwadratów	60	24	O
Dwudziesto-dwunastościan (3.5.3.5)				32	20 trójkątów 12 pięciokątów	60	30	Ih
Dwunastościan ścięty (3.10.10)				32	20 trójkątów 12 dziesięciokątów	90	60	Ih
Dwudziestościan ścięty (5.6.6)				32	12 pięciokątów 20 sześciokątów	90	60	Ih
Dwudziesto-dwunastościan rombowy mały (3.4.5.4)				62	20 trójkątów 30 kwadratów 12 pięciokątów	120	60	Ih
Dwudziesto-dwunastościan rombowy wielki (4.6.10)				62	30 kwadratów 20 sześciokątów 12 dziesięciokątów	180	120	Ih
Dwudziesto-dwunastościan przycięty (3.3.3.3.5)				92	80 trójkątów 12 pięciokątów	150	60	I

Uwagi

1. Można spotkać definicje pozbawione warunku wierzchołkowej tranzytywności. Wówczas do wielościanów foremnych zaliczany jest również pseudo sześcio-ośmiościan rombowy mały^[2].