Pentellated 6-orthoplexes

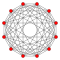
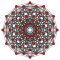
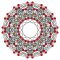
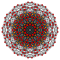
In six-dimensional geometry, a pentellated 6-orthoplex is a convex uniform 6-polytope with 5th order truncations of the regular 6-orthoplex.

Orthogonal projections in B6 Coxeter plane
6-orthoplex	Pentellated 6-orthoplex Pentellated 6-cube	6-cube	Pentitruncated 6-orthoplex
Penticantellated 6-orthoplex	Penticantitruncated 6-orthoplex	Pentiruncitruncated 6-orthoplex	Pentiruncicantellated 6-cube
Pentiruncicantitruncated 6-orthoplex	Pentisteritruncated 6-cube	Pentistericantitruncated 6-orthoplex	Pentisteriruncicantitruncated 6-orthoplex (Omnitruncated 6-cube)

There are unique 16 degrees of pentellations of the 6-orthoplex with permutations of truncations, cantellations, runcinations, and sterications. Ten are shown, with the other 6 more easily constructed as a pentellated 6-cube. The simple pentellated 6-orthoplex (Same as pentellated 5-cube) is also called an expanded 6-orthoplex, constructed by an expansion operation applied to the regular 6-orthoplex. The highest form, the pentisteriruncicantitruncated 6-orthoplex, is called an omnitruncated 6-orthoplex with all of the nodes ringed.

Pentitruncated 6-orthoplex

Pentitruncated 6-orthoplex
Type	uniform 6-polytope
Schläfli symbol	t0,1,5{3,3,3,3,4}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	8640
Vertices	1920
Vertex figure
Coxeter groups	B6, [4,3,3,3,3]
Properties	convex

Alternate names

• Teritruncated hexacontatetrapeton (Acronym: tacox) (Jonathan Bowers)^[1]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Penticantellated 6-orthoplex

Penticantellated 6-orthoplex
Type	uniform 6-polytope
Schläfli symbol	t0,2,5{3,3,3,3,4}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	21120
Vertices	3840
Vertex figure
Coxeter groups	B6, [4,3,3,3,3]
Properties	convex

Alternate names

• Terirhombated hexacontitetrapeton (Acronym: tapox) (Jonathan Bowers)^[2]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Penticantitruncated 6-orthoplex

Penticantitruncated 6-orthoplex
Type	uniform 6-polytope
Schläfli symbol	t0,1,2,5{3,3,3,3,4}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	30720
Vertices	7680
Vertex figure
Coxeter groups	B6, [4,3,3,3,3]
Properties	convex

Alternate names

• Terigreatorhombated hexacontitetrapeton (Acronym: togrig) (Jonathan Bowers)^[3]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentiruncitruncated 6-orthoplex

Pentiruncitruncated 6-orthoplex
Type	uniform 6-polytope
Schläfli symbol	t0,1,3,5{3,3,3,3,4}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	51840
Vertices	11520
Vertex figure
Coxeter groups	B6, [4,3,3,3,3]
Properties	convex

Alternate names

• Teriprismatotruncated hexacontitetrapeton (Acronym: tocrax) (Jonathan Bowers)^[4]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentiruncicantitruncated 6-orthoplex

Pentiruncicantitruncated 6-orthoplex
Type	uniform 6-polytope
Schläfli symbol	t0,1,2,3,5{3,3,3,3,4}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	80640
Vertices	23040
Vertex figure
Coxeter groups	B6, [4,3,3,3,3]
Properties	convex

Alternate names

• Terigreatoprismated hexacontitetrapeton (Acronym: tagpog) (Jonathan Bowers)^[5]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Pentistericantitruncated 6-orthoplex

Pentistericantitruncated 6-orthoplex
Type	uniform 6-polytope
Schläfli symbol	t0,1,2,4,5{3,3,3,3,4}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges	80640
Vertices	23040
Vertex figure
Coxeter groups	B6, [4,3,3,3,3]
Properties	convex

Alternate names

• Tericelligreatorhombated hexacontitetrapeton (Acronym: tecagorg) (Jonathan Bowers)^[6]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Related polytopes

These polytopes are from a set of 63 uniform 6-polytopes generated from the B₆ Coxeter plane, including the regular 6-cube or 6-orthoplex.

B6 polytopes
β6	t1β6	t2β6	t2γ6	t1γ6	γ6	t0,1β6	t0,2β6
t1,2β6	t0,3β6	t1,3β6	t2,3γ6	t0,4β6	t1,4γ6	t1,3γ6	t1,2γ6
t0,5γ6	t0,4γ6	t0,3γ6	t0,2γ6	t0,1γ6	t0,1,2β6	t0,1,3β6	t0,2,3β6
t1,2,3β6	t0,1,4β6	t0,2,4β6	t1,2,4β6	t0,3,4β6	t1,2,4γ6	t1,2,3γ6	t0,1,5β6
t0,2,5β6	t0,3,4γ6	t0,2,5γ6	t0,2,4γ6	t0,2,3γ6	t0,1,5γ6	t0,1,4γ6	t0,1,3γ6
t0,1,2γ6	t0,1,2,3β6	t0,1,2,4β6	t0,1,3,4β6	t0,2,3,4β6	t1,2,3,4γ6	t0,1,2,5β6	t0,1,3,5β6
t0,2,3,5γ6	t0,2,3,4γ6	t0,1,4,5γ6	t0,1,3,5γ6	t0,1,3,4γ6	t0,1,2,5γ6	t0,1,2,4γ6	t0,1,2,3γ6
t0,1,2,3,4β6	t0,1,2,3,5β6	t0,1,2,4,5β6	t0,1,2,4,5γ6	t0,1,2,3,5γ6	t0,1,2,3,4γ6	t0,1,2,3,4,5γ6

Notes

1. Klitzing, (x4o3o3o3x3x - tacox)
2. Klitzing, (x4o3o3x3o3x - tapox)
3. Klitzing, (x4o3o3x3x3x - togrig)
4. Klitzing, (x4o3x3o3x3x - tocrax)
5. Klitzing, (x4x3o3x3x3x - tagpog)
6. Klitzing, (x4x3o3x3x3x - tecagorg)

References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
• Klitzing, Richard. "6D uniform polytopes (polypeta)". x4o3o3o3x3x - tacox, x4o3o3x3o3x - tapox, x4o3o3x3x3x - togrig, x4o3x3o3x3x - tocrax, x4x3o3x3x3x - tagpog, x4x3o3x3x3x - tecagorg

External links

• Glossary for hyperspace, George Olshevsky.
• Polytopes of Various Dimensions
• Multi-dimensional Glossary

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds