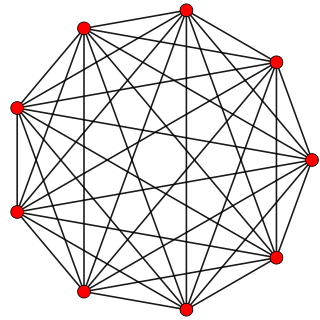
8-simplex

In geometry, an 8-simplex is a self-dual regular 8-polytope. It has 9 vertices, 36 edges, 84 triangle faces, 126 tetrahedral cells, 126 5-cell 4-faces, 84 5-simplex 5-faces, 36 6-simplex 6-faces, and 9 7-simplex 7-faces. Its dihedral angle is cos⁻¹(1/8), or approximately 82.82°.

Regular enneazetton (8-simplex)
Orthogonal projection inside Petrie polygon
Type	Regular 8-polytope
Family	simplex
Schläfli symbol	{3,3,3,3,3,3,3}
Coxeter-Dynkin diagram
7-faces	9 7-simplex
6-faces	36 6-simplex
5-faces	84 5-simplex
4-faces	126 5-cell
Cells	126 tetrahedron
Faces	84 triangle
Edges	36
Vertices	9
Vertex figure	7-simplex
Petrie polygon	enneagon
Coxeter group	A8 [3,3,3,3,3,3,3]
Dual	Self-dual
Properties	convex

It can also be called an enneazetton, or ennea-8-tope, as a 9-facetted polytope in eight-dimensions. The name enneazetton is derived from ennea for nine facets in Greek and -zetta for having seven-dimensional facets, and -on.

As a configuration

This configuration matrix represents the 8-simplex. The rows and columns correspond to vertices, edges, faces, cells, 4-faces, 5-faces, 6-faces and 7-faces. The diagonal numbers say how many of each element occur in the whole 8-simplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element. This self-dual simplex's matrix is identical to its 180 degree rotation.^[1][2]

${\displaystyle {\begin{bmatrix}{\begin{matrix}9&8&28&56&70&56&28&8\\2&36&7&21&35&35&21&7\\3&3&84&6&15&20&15&6\\4&6&4&126&5&10&10&5\\5&10&10&5&126&4&6&4\\6&15&20&15&6&84&3&3\\7&21&35&35&21&7&36&2\\8&28&56&70&56&28&8&9\end{matrix}}\end{bmatrix}}}$

Coordinates

The Cartesian coordinates of the vertices of an origin-centered regular enneazetton having edge length 2 are:

${\displaystyle \left(1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ {\sqrt {1/3}},\ \pm 1\right)}$

${\displaystyle \left(1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ -2{\sqrt {1/3}},\ 0\right)}$

${\displaystyle \left(1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ -{\sqrt {3/2}},\ 0,\ 0\right)}$

${\displaystyle \left(1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ -2{\sqrt {2/5}},\ 0,\ 0,\ 0\right)}$

${\displaystyle \left(1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ -{\sqrt {5/3}},\ 0,\ 0,\ 0,\ 0\right)}$

${\displaystyle \left(1/6,\ {\sqrt {1/28}},\ -{\sqrt {12/7}},\ 0,\ 0,\ 0,\ 0,\ 0\right)}$

${\displaystyle \left(1/6,\ -{\sqrt {7/4}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}$

${\displaystyle \left(-4/3,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}$

More simply, the vertices of the 8-simplex can be positioned in 9-space as permutations of (0,0,0,0,0,0,0,0,1). This construction is based on facets of the 9-orthoplex.

Another origin-centered construction uses (1,1,1,1,1,1,1,1)/3 and permutations of (1,1,1,1,1,1,1,-11)/12 for edge length √2.

Images

orthographic projections

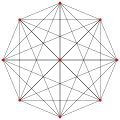
Ak Coxeter plane	A8	A7	A6	A5
Graph
Dihedral symmetry	[9]	[8]	[7]	[6]
Ak Coxeter plane	A4	A3	A2
Graph
Dihedral symmetry	[5]	[4]	[3]

Related polytopes and honeycombs

This polytope is a facet in the uniform tessellations: 2₅₁, and 5₂₁ with respective Coxeter-Dynkin diagrams:

,

This polytope is one of 135 uniform 8-polytopes with A₈ symmetry.

A8 polytopes
t0	t1	t2	t3	t01	t02	t12	t03	t13	t23	t04	t14	t24	t34	t05
t15	t25	t06	t16	t07	t012	t013	t023	t123	t014	t024	t124	t034	t134	t234
t015	t025	t125	t035	t135	t235	t045	t145	t016	t026	t126	t036	t136	t046	t056
t017	t027	t037	t0123	t0124	t0134	t0234	t1234	t0125	t0135	t0235	t1235	t0145	t0245	t1245
t0345	t1345	t2345	t0126	t0136	t0236	t1236	t0146	t0246	t1246	t0346	t1346	t0156	t0256	t1256
t0356	t0456	t0127	t0137	t0237	t0147	t0247	t0347	t0157	t0257	t0167	t01234	t01235	t01245	t01345
t02345	t12345	t01236	t01246	t01346	t02346	t12346	t01256	t01356	t02356	t12356	t01456	t02456	t03456	t01237
t01247	t01347	t02347	t01257	t01357	t02357	t01457	t01267	t01367	t012345	t012346	t012356	t012456	t013456	t023456
t123456	t012347	t012357	t012457	t013457	t023457	t012367	t012467	t013467	t012567	t0123456	t0123457	t0123467	t0123567	t01234567

References

1. Coxeter 1973, §1.8 Configurations
2. Coxeter, H.S.M. (1991). Regular Complex Polytopes (2nd ed.). Cambridge University Press. p. 117. ISBN 9780521394901.

• Coxeter, H.S.M.:
  • — (1973). "Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)". Regular Polytopes (3rd ed.). Dover. pp. 296. ISBN 0-486-61480-8.
  • Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic, eds. (1995). Kaleidoscopes: Selected Writings of H.S.M. Coxeter. Wiley. ISBN 978-0-471-01003-6.
    • (Paper 22) — (1940). "Regular and Semi Regular Polytopes I". Math. Zeit. 46: 380–407. doi:10.1007/BF01181449. S2CID 186237114.
    • (Paper 23) — (1985). "Regular and Semi-Regular Polytopes II". Math. Zeit. 188 (4): 559–591. doi:10.1007/BF01161657. S2CID 120429557.
    • (Paper 24) — (1988). "Regular and Semi-Regular Polytopes III". Math. Zeit. 200: 3–45. doi:10.1007/BF01161745. S2CID 186237142.
• Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "26. Hemicubes: 1_n1". The Symmetries of Things. p. 409. ISBN 978-1-56881-220-5.
• Johnson, Norman (1991). "Uniform Polytopes" (Manuscript). Norman Johnson (mathematician).
  • Johnson, N.W. (1966). The Theory of Uniform Polytopes and Honeycombs (PhD). University of Toronto. OCLC 258527038.
• Klitzing, Richard. "8D uniform polytopes (polyzetta) x3o3o3o3o3o3o3o — ene".

External links

• Glossary for hyperspace, George Olshevsky.
• Polytopes of Various Dimensions
• Multi-dimensional Glossary

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds