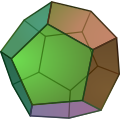
Regular polytope
Polytope with highest degree of symmetry From Wikipedia, the free encyclopedia
In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (July 2014) |
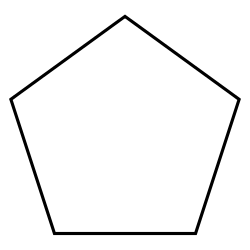 A regular pentagon is a polygon, a two-dimensional polytope with 5 edges, represented by Schläfli symbol {5}. |
 A regular dodecahedron is a polyhedron, a three-dimensional polytope, with 12 pentagonal faces, represented by Schläfli symbol {5,3}. |
 A regular 120-cell is a polychoron, a four-dimensional polytope, with 120 dodecahedral cells, represented by Schläfli symbol {5,3,3}. (shown here as a Schlegel diagram) |
 A regular cubic honeycomb is a tessellation, an infinite polytope, represented by Schläfli symbol {4,3,4}. |
 The 256 vertices and 1024 edges of an 8-cube can be shown in this orthogonal projection (Petrie polygon) | |
Regular polytopes are the generalised analog in any number of dimensions of regular polygons (for example, the square or the regular pentagon) and regular polyhedra (for example, the cube). The strong symmetry of the regular polytopes gives them an aesthetic quality that interests both mathematicians and non-mathematicians.
Classically, a regular polytope in n dimensions may be defined as having regular facets ([n–1]-faces) and regular vertex figures. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytopes.
A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ..., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.
Classification and description
Summarize
Perspective
Regular polytopes are classified primarily according to their dimension.
Three classes of regular polytopes exist in every number of dimensions:
- Regular simplex
- Measure polytope (Hypercube)
- Cross polytope (Orthoplex)
Any other regular polytope is said to be exceptional.
In one dimension, the line segment simultaneously serves as the 1-simplex, the 1-hypercube and the 1-orthoplex.
In two dimensions, there are infinitely many regular polygons, namely the regular n-sided polygon for n ≥ 3. The triangle is the 2-simplex. The square is both the 2-hypercube and the 2-orthoplex. The n-sided polygons for n ≥ 5 are exceptional.
In three and four dimensions, there are several more exceptional regular polyhedra and 4-polytopes respectively.
In five dimensions and above, the simplex, hypercube and orthoplex are the only regular polytopes. There are no exceptional regular polytopes in these dimensions.
Regular polytopes can be further classified according to symmetry. For example, the cube and the regular octahedron share the same symmetry, as do the regular dodecahedron and regular icosahedron. Two distinct regular polytopes with the same symmetry are dual to one another. Indeed, symmetry groups are sometimes named after regular polytopes, for example the tetrahedral and icosahedral symmetries.
The idea of a polytope is sometimes generalised to include related kinds of geometrical object. Some of these have regular examples, as discussed in the section on historical discovery below.
Schläfli symbols
A concise symbolic representation for regular polytopes was developed by Ludwig Schläfli in the 19th century, and a slightly modified form has become standard. The notation is best explained by adding one dimension at a time.
- A convex regular polygon having n sides is denoted by {n}. So an equilateral triangle is {3}, a square {4}, and so on indefinitely. A regular n-sided star polygon which winds m times around its centre is denoted by the fractional value {n/m}, where n and m are co-prime, so a regular pentagram is {5/2}.
- A regular polyhedron having faces {n} with p faces joining around a vertex is denoted by {n, p}. The nine regular polyhedra are {3, 3}; {3, 4}; {4, 3}; {3, 5}; {5, 3}; {3, 5/2}; {5/2, 3}; {5, 5/2}; and {5/2, 5}. {p} is the vertex figure of the polyhedron.
- A regular 4-polytope having cells {n, p} with q cells joining around an edge is denoted by {n, p, q}. The vertex figure of the 4-polytope is a {p, q}.
- A regular 5-polytope is an {n, p, q, r}. And so on.
Duality of the regular polytopes
The dual of a regular polytope is also a regular polytope. The Schläfli symbol for the dual polytope is just the original symbol written backwards: {3, 3} is self-dual, {3, 4} is dual to {4, 3}, {4, 3, 3} to {3, 3, 4} and so on.
The vertex figure of a regular polytope is the dual of the dual polytope's facet. For example, the vertex figure of {3, 3, 4} is {3, 4}, the dual of which is {4, 3} — a cell of {4, 3, 3}.
The measure and cross polytopes in any dimension are dual to each other.
If the Schläfli symbol is palindromic (i.e. reads the same forwards and backwards), then the polytope is self-dual. The self-dual regular polytopes are:
- All regular polygons - {a}.
- All regular n-simplexes - {3,3,...,3}.
- The regular 24-cell - {3,4,3} - in 4 dimensions.
- The great 120-cell - {5,5/2,5} - and grand stellated 120-cell - {5/2,5,5/2} - in 4 dimensions.
- All regular n-dimensional hypercubic honeycombs - {4,3,...,3,4}. These may be treated as infinite polytopes.
- Hyperbolic tilings and honeycombs (tilings {p,p} with p>4 in 2 dimensions; {4,4,4}, {5,3,5}, {3,5,3}, {6,3,6}, and {3,6,3} in 3 dimensions; {5,3,3,5} in 4 dimensions; and {3,3,4,3,3} in 5 dimensions).
Regular simplices
 |
 |
 |
 |
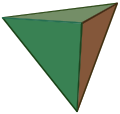
| Line segment | Triangle | Tetrahedron | Pentachoron |
 |
 |
 |
These are the regular simplices or simplexes. Their names are, in order of dimension:
- 0. Point
- 1. Line segment
- 2. Equilateral triangle (regular trigon)
- 3. Regular tetrahedron (triangular pyramid)
- 4. Regular pentachoron or 4-simplex
- 5. Regular hexateron or 5-simplex
- ... An n-simplex has n+1 vertices.
The process of making each simplex can be visualised on a graph: Begin with a point A. Mark point B at a distance r from it, and join to form a line segment. Mark point C in a second, orthogonal, dimension at a distance r from both, and join to A and B to form an equilateral triangle. Mark point D in a third, orthogonal, dimension a distance r from all three, and join to form a regular tetrahedron. This process is repeated further using new points to form higher-dimensional simplices.
Measure polytopes (hypercubes)
 |
 |
 |
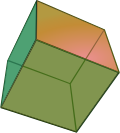
| Square | Cube | Tesseract |
 |
 |
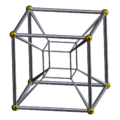 |
These are the measure polytopes or hypercubes. Their names are, in order of dimension:
- 0. Point
- 1. Line segment
- 2. Square (regular tetragon)
- 3. Cube (regular hexahedron)
- 4. Tesseract (regular octachoron) or 4-cube
- 5. Penteract (regular decateron) or 5-cube
- ... An n-cube has 2n vertices.
The process of making each hypercube can be visualised on a graph: Begin with a point A. Extend a line to point B at distance r, and join to form a line segment. Extend a second line of length r, orthogonal to AB, from B to C, and likewise from A to D, to form a square ABCD. Extend lines of length r respectively from each corner, orthogonal to both AB and BC (i.e. upwards). Mark new points E,F,G,H to form the cube ABCDEFGH. This process is repeated further using new lines to form higher-dimensional hypercubes.
Cross polytopes (orthoplexes)
 |
 |
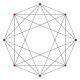 |
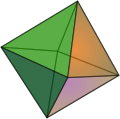
| Square | Octahedron | 16-cell |
 |
 |
 |
These are the cross polytopes or orthoplexes. Their names are, in order of dimensionality:
- 0. Point
- 1. Line segment
- 2. Square (regular tetragon)
- 3. Regular octahedron
- 4. Regular hexadecachoron (16-cell) or 4-orthoplex
- 5. Regular triacontakaiditeron (pentacross) or 5-orthoplex
- ... An n-orthoplex has 2n vertices.
The process of making each orthoplex can be visualised on a graph: Begin with a point O. Extend a line in opposite directions to points A and B a distance r from O and 2r apart. Draw a line COD of length 2r, centred on O and orthogonal to AB. Join the ends to form a square ACBD. Draw a line EOF of the same length and centered on 'O', orthogonal to AB and CD (i.e. upwards and downwards). Join the ends to the square to form a regular octahedron. This process is repeated further using new lines to form higher-dimensional orthoplices.
Classification by Coxeter groups
Regular polytopes can be classified by their isometry group. These are finite Coxeter groups, but not every finite Coxeter group may be realised as the isometry group of a regular polytope. Regular polytopes are in bijection with Coxeter groups with linear Coxeter-Dynkin diagram (without branch point) and an increasing numbering of the nodes. Reversing the numbering gives the dual polytope.
The classification of finite Coxeter groups, which goes back to (Coxeter 1935), therefore implies the classification of regular polytopes:
- Type , the symmetric group, gives the regular simplex,
- Type , gives the measure polytope and the cross polytope (both can be distinguished by the increasing numbering of the nodes of the Coxeter-Dynkin diagram),
- Exceptional types give the regular polygons (with ),
- Exceptional type gives the regular dodecahedron and icosahedron (again the numbering allows to distinguish them),
- Exceptional type gives the 120-cell and the 600-cell,
- Exceptional type gives the 24-cell, which is self-dual.
The bijection between regular polytopes and Coxeter groups with linear Coxeter-Dynkin diagram can be understood as follows. Consider a regular polytope of dimension and take its barycentric subdivision. The fundamental domain of the isometry group action on is given by any simplex in the barycentric subdivision. The simplex has vertices which can be numbered from 0 to by the dimension of the corresponding face of (the face they are the barycenter of). The isometry group of is generated by the reflections around the hyperplanes of containing the vertex number (since the barycenter of the whole polytope is fixed by any isometry). These hyperplanes can be numbered by the vertex of they do not contain. The remaining thing to check is that any two hyperplanes with adjacent numbers cannot be orthogonal, whereas hyperplanes with non-adjacent numbers are orthogonal. This can be done using induction (since all facets of are again regular polytopes). Therefore, the Coxeter-Dynkin diagram of the isometry group of has vertices numbered from 0 to such that adjacent numbers are linked by at least one edge and non-adjacent numbers are not linked.
History of discovery
Summarize
Perspective
Convex polygons and polyhedra
The earliest surviving mathematical treatment of regular polygons and polyhedra comes to us from ancient Greek mathematicians. The five Platonic solids were known to them. Pythagoras knew of at least three of them and Theaetetus (c. 417 BC – 369 BC) described all five. Later, Euclid wrote a systematic study of mathematics, publishing it under the title Elements, which built up a logical theory of geometry and number theory. His work concluded with mathematical descriptions of the five Platonic solids.
Star polygons and polyhedra
Our understanding remained static for many centuries after Euclid. The subsequent history of the regular polytopes can be characterised by a gradual broadening of the basic concept, allowing more and more objects to be considered among their number. Thomas Bradwardine (Bradwardinus) was the first to record a serious study of star polygons. Various star polyhedra appear in Renaissance art, but it was not until Johannes Kepler studied the small stellated dodecahedron and the great stellated dodecahedron in 1619 that he realised these two polyhedra were regular. Louis Poinsot discovered the great dodecahedron and great icosahedron in 1809, and Augustin Cauchy proved the list complete in 1812. These polyhedra are known as collectively as the Kepler-Poinsot polyhedra.
| Kepler-Poinsot polyhedra | |||
 |
 |
 |
 |
| Small stellated dodecahedron | Great stellated dodecahedron | Great dodecahedron | Great icosahedron |
Higher-dimensional polytopes

It was not until the 19th century that a Swiss mathematician, Ludwig Schläfli, examined and characterised the regular polytopes in higher dimensions. His efforts were first published in full in Schläfli (1901), six years posthumously, although parts of it were published in Schläfli (1855) and Schläfli (1858). Between 1880 and 1900, Schläfli's results were rediscovered independently by at least nine other mathematicians — see Coxeter (1973, pp. 143–144) for more details. Schläfli called such a figure a "polyschem" (in English, "polyscheme" or "polyschema"). The term "polytope" was introduced by Reinhold Hoppe, one of Schläfli's rediscoverers, in 1882, and first used in English by Alicia Boole Stott some twenty years later. The term "polyhedroids" was also used in earlier literature (Hilbert, 1952).
Coxeter (1973) is probably the most comprehensive printed treatment of Schläfli's and similar results to date. Schläfli showed that there are six regular convex polytopes in 4 dimensions. Five of them can be seen as analogous to the Platonic solids: the 4-simplex (or pentachoron) to the tetrahedron, the hypercube (or tesseract) to the cube, the 4-orthoplex (or hexadecachoron or 16-cell) to the octahedron, the 120-cell to the dodecahedron, and the 600-cell to the icosahedron. The sixth, the 24-cell, can be seen as a transitional form between the hypercube and 16-cell, analogous to the way that the cuboctahedron and the rhombic dodecahedron are transitional forms between the cube and the octahedron.
In five and more dimensions, there are exactly three finite regular polytopes, which correspond to the tetrahedron, cube and octahedron: these are the regular simplices, measure polytopes and cross polytopes. Descriptions of these may be found in the list of regular polytopes. Also of interest are the star regular 4-polytopes, partially discovered by Schläfli.
By the end of the 19th century, mathematicians such as Arthur Cayley and Ludwig Schläfli had developed the theory of regular polytopes in four and higher dimensions, such as the tesseract and the 24-cell.
The latter are difficult (though not impossible) to visualise through a process of dimensional analogy, since they retain the familiar symmetry of their lower-dimensional analogues. The tesseract contains 8 cubical cells. It consists of two cubes in parallel hyperplanes with corresponding vertices cross-connected in such a way that the 8 cross-edges are equal in length and orthogonal to the 12+12 edges situated on each cube. The corresponding faces of the two cubes are connected to form the remaining 6 cubical faces of the tesseract. The 24-cell can be derived from the tesseract by joining the 8 vertices of each of its cubical faces to an additional vertex to form the four-dimensional analogue of a pyramid. Both figures, as well as other 4-dimensional figures, can be directly visualised and depicted using 4-dimensional stereographs.[1]
Harder still to imagine are the more modern abstract regular polytopes such as the 57-cell or the 11-cell. From the mathematical point of view, however, these objects have the same aesthetic qualities as their more familiar two and three-dimensional relatives.
At the start of the 20th century, the definition of a regular polytope was as follows.
- A regular polygon is a polygon whose edges are all equal and whose angles are all equal.
- A regular polyhedron is a polyhedron whose faces are all congruent regular polygons, and whose vertex figures are all congruent and regular.
- And so on, a regular n-polytope is an n-dimensional polytope whose (n − 1)-dimensional faces are all regular and congruent, and whose vertex figures are all regular and congruent.
This is a "recursive" definition. It defines regularity of higher dimensional figures in terms of regular figures of a lower dimension. There is an equivalent (non-recursive) definition, which states that a polytope is regular if it has a sufficient degree of symmetry.
- An n-polytope is regular if any set consisting of a vertex, an edge containing it, a 2-dimensional face containing the edge, and so on up to n−1 dimensions, can be mapped to any other such set by a symmetry of the polytope.
So for example, the cube is regular because if we choose a vertex of the cube, and one of the three edges it is on, and one of the two faces containing the edge, then this triplet, known as a flag, (vertex, edge, face) can be mapped to any other such flag by a suitable symmetry of the cube. Thus we can define a regular polytope very succinctly:
- A regular polytope is one whose symmetry group is transitive on its flags.
In the 20th century, some important developments were made. The symmetry groups of the classical regular polytopes were generalised into what are now called Coxeter groups. Coxeter groups also include the symmetry groups of regular tessellations of space or of the plane. For example, the symmetry group of an infinite chessboard would be the Coxeter group [4,4].
Apeirotopes — infinite polytopes
In the first part of the 20th century, Coxeter and Petrie discovered three infinite structures: {4, 6}, {6, 4} and {6, 6}. They called them regular skew polyhedra, because they seemed to satisfy the definition of a regular polyhedron — all the vertices, edges and faces are alike, all the angles are the same, and the figure has no free edges. Nowadays, they are called infinite polyhedra or apeirohedra. The regular tilings of the plane {4, 4}, {3, 6} and {6, 3} can also be regarded as infinite polyhedra.
In the 1960s Branko Grünbaum issued a call to the geometric community to consider more abstract types of regular polytopes that he called polystromata. He developed the theory of polystromata, showing examples of new objects he called regular apeirotopes, that is, regular polytopes with infinitely many faces. A simple example of a skew apeirogon would be a zig-zag. It seems to satisfy the definition of a regular polygon — all the edges are the same length, all the angles are the same, and the figure has no loose ends (because they can never be reached). More importantly, perhaps, there are symmetries of the zig-zag that can map any pair of a vertex and attached edge to any other. Since then, other regular apeirogons and higher apeirotopes have continued to be discovered.
Regular complex polytopes
A complex number has a real part, which is the bit we are all familiar with, and an imaginary part, which is a multiple of the square root of minus one. A complex Hilbert space has its x, y, z, etc. coordinates as complex numbers. This effectively doubles the number of dimensions. A polytope constructed in such a unitary space is called a complex polytope.[2]
Abstract polytopes

Grünbaum also discovered the 11-cell, a four-dimensional self-dual object whose facets are not icosahedra, but are "hemi-icosahedra" — that is, they are the shape one gets if one considers opposite faces of the icosahedra to be actually the same face (Grünbaum 1976). The hemi-icosahedron has only 10 triangular faces, and 6 vertices, unlike the icosahedron, which has 20 and 12.
This concept may be easier for the reader to grasp if one considers the relationship of the cube and the hemicube. An ordinary cube has 8 corners, they could be labeled A to H, with A opposite H, B opposite G, and so on. In a hemicube, A and H would be treated as the same corner. So would B and G, and so on. The edge AB would become the same edge as GH, and the face ABEF would become the same face as CDGH. The new shape has only three faces, 6 edges and 4 corners.
The 11-cell cannot be formed with regular geometry in flat (Euclidean) hyperspace, but only in positively curved (elliptic) hyperspace.
A few years after Grünbaum's discovery of the 11-cell, H. S. M. Coxeter independently discovered the same shape. He had earlier discovered a similar polytope, the 57-cell (Coxeter 1982, 1984).
By 1994 Grünbaum was considering polytopes abstractly as combinatorial sets of points or vertices, and was unconcerned whether faces were planar. As he and others refined these ideas, such sets came to be called abstract polytopes. An abstract polytope is defined as a partially ordered set (poset), whose elements are the polytope's faces (vertices, edges, faces etc.) ordered by containment. Certain restrictions are imposed on the set that are similar to properties satisfied by the classical regular polytopes (including the Platonic solids). The restrictions, however, are loose enough that regular tessellations, hemicubes, and even objects as strange as the 11-cell or stranger, are all examples of regular polytopes.
A geometric polytope is understood to be a realization of the abstract polytope, such that there is a one-to-one mapping from the abstract elements to the corresponding faces of the geometric realisation. Thus, any geometric polytope may be described by the appropriate abstract poset, though not all abstract polytopes have proper geometric realizations.
The theory has since been further developed, largely by McMullen & Schulte (2002), but other researchers have also made contributions.
Regularity of abstract polytopes
Regularity has a related, though different meaning for abstract polytopes, since angles and lengths of edges have no meaning.
The definition of regularity in terms of the transitivity of flags as given in the introduction applies to abstract polytopes.
Any classical regular polytope has an abstract equivalent which is regular, obtained by taking the set of faces. But non-regular classical polytopes can have regular abstract equivalents, since abstract polytopes do not retain information about angles and edge lengths, for example. And a regular abstract polytope may not be realisable as a classical polytope.
All polygons are regular in the abstract world, for example, whereas only those having equal angles and edges of equal length are regular in the classical world.
Vertex figure of abstract polytopes
The concept of vertex figure is also defined differently for an abstract polytope. The vertex figure of a given abstract n-polytope at a given vertex V is the set of all abstract faces which contain V, including V itself. More formally, it is the abstract section
- Fn / V = {F | V ≤ F ≤ Fn}
where Fn is the maximal face, i.e. the notional n-face which contains all other faces. Note that each i-face, i ≥ 0 of the original polytope becomes an (i − 1)-face of the vertex figure.
Unlike the case for Euclidean polytopes, an abstract polytope with regular facets and vertex figures may or may not be regular itself – for example, the square pyramid, all of whose facets and vertex figures are regular abstract polygons.
The classical vertex figure will, however, be a realisation of the abstract one.
Constructions
Summarize
Perspective
Polygons
The traditional way to construct a regular polygon, or indeed any other figure on the plane, is by compass and straightedge. Constructing some regular polygons in this way is very simple (the easiest is perhaps the equilateral triangle), some are more complex, and some are impossible ("not constructible"). The simplest few regular polygons that are impossible to construct are the n-sided polygons with n equal to 7, 9, 11, 13, 14, 18, 19, 21,...
Constructibility in this sense refers only to ideal constructions with ideal tools. Of course reasonably accurate approximations can be constructed by a range of methods; while theoretically possible constructions may be impractical.
Polyhedra
Euclid's Elements gave what amount to ruler-and-compass constructions for the five Platonic solids.[3] However, the merely practical question of how one might draw a straight line in space, even with a ruler, might lead one to question what exactly it means to "construct" a regular polyhedron. (One could ask the same question about the polygons, of course.)

The English word "construct" has the connotation of systematically building the thing constructed. The most common way presented to construct a regular polyhedron is via a fold-out net. To obtain a fold-out net of a polyhedron, one takes the surface of the polyhedron and cuts it along just enough edges so that the surface may be laid out flat. This gives a plan for the net of the unfolded polyhedron. Since the Platonic solids have only triangles, squares and pentagons for faces, and these are all constructible with a ruler and compass, there exist ruler-and-compass methods for drawing these fold-out nets. The same applies to star polyhedra, although here we must be careful to make the net for only the visible outer surface.
If this net is drawn on cardboard, or similar foldable material (for example, sheet metal), the net may be cut out, folded along the uncut edges, joined along the appropriate cut edges, and so forming the polyhedron for which the net was designed. For a given polyhedron there may be many fold-out nets. For example, there are 11 for the cube, and over 900000 for the dodecahedron.[4]
Numerous children's toys, generally aimed at the teen or pre-teen age bracket, allow experimentation with regular polygons and polyhedra. For example, klikko provides sets of plastic triangles, squares, pentagons and hexagons that can be joined edge-to-edge in a large number of different ways. A child playing with such a toy could rediscover the Platonic solids (or the Archimedean solids), especially if given a little guidance from a knowledgeable adult.
In theory, almost any material may be used to construct regular polyhedra.[5] They may be carved out of wood, modeled out of wire, formed from stained glass. The imagination is the limit.
Higher dimensions



In higher dimensions, it becomes harder to say what one means by "constructing" the objects. Clearly, in a 3-dimensional universe, it is impossible to build a physical model of an object having 4 or more dimensions. There are several approaches normally taken to overcome this matter.
The first approach, suitable for four dimensions, uses four-dimensional stereography.[1] Depth in a third dimension is represented with horizontal relative displacement, depth in a fourth dimension with vertical relative displacement between the left and right images of the stereograph.
The second approach is to embed the higher-dimensional objects in three-dimensional space, using methods analogous to the ways in which three-dimensional objects are drawn on the plane. For example, the fold out nets mentioned in the previous section have higher-dimensional equivalents.[6] One might even imagine building a model of this fold-out net, as one draws a polyhedron's fold-out net on a piece of paper. Sadly, we could never do the necessary folding of the 3-dimensional structure to obtain the 4-dimensional polytope because of the constraints of the physical universe. Another way to "draw" the higher-dimensional shapes in 3 dimensions is via some kind of projection, for example, the analogue of either orthographic or perspective projection. Coxeter's famous book on polytopes (Coxeter 1973) has some examples of such orthographic projections.[7] Note that immersing even 4-dimensional polychora directly into two dimensions is quite confusing. Easier to understand are 3-d models of the projections. Such models are occasionally found in science museums or mathematics departments of universities (such as that of the Université Libre de Bruxelles).
The intersection of a four (or higher) dimensional regular polytope with a three-dimensional hyperplane will be a polytope (not necessarily regular). If the hyperplane is moved through the shape, the three-dimensional slices can be combined, animated into a kind of four dimensional object, where the fourth dimension is taken to be time. In this way, we can see (if not fully grasp) the full four-dimensional structure of the four-dimensional regular polytopes, via such cutaway cross sections. This is analogous to the way a CAT scan reassembles two-dimensional images to form a 3-dimensional representation of the organs being scanned. The ideal would be an animated hologram of some sort, however, even a simple animation such as the one shown can already give some limited insight into the structure of the polytope.
Another way a three-dimensional viewer can comprehend the structure of a four-dimensional polytope is through being "immersed" in the object, perhaps via some form of virtual reality technology. To understand how this might work, imagine what one would see if space were filled with cubes. The viewer would be inside one of the cubes, and would be able to see cubes in front of, behind, above, below, to the left and right of himself. If one could travel in these directions, one could explore the array of cubes, and gain an understanding of its geometrical structure. An infinite array of cubes is not a polytope in the traditional sense. In fact, it is a tessellation of 3-dimensional (Euclidean) space. However, a 4-polytope can be considered a tessellation of a 3-dimensional non-Euclidean space, namely, a tessellation of the surface of a four-dimensional sphere (a 4-dimensional spherical tiling).

Locally, this space seems like the one we are familiar with, and therefore, a virtual-reality system could, in principle, be programmed to allow exploration of these "tessellations", that is, of the 4-dimensional regular polytopes. The mathematics department at UIUC has a number of pictures of what one would see if embedded in a tessellation of hyperbolic space with dodecahedra. Such a tessellation forms an example of an infinite abstract regular polytope.
Normally, for abstract regular polytopes, a mathematician considers that the object is "constructed" if the structure of its symmetry group is known. This is because of an important theorem in the study of abstract regular polytopes, providing a technique that allows the abstract regular polytope to be constructed from its symmetry group in a standard and straightforward manner.
Regular polytopes in nature
For examples of polygons in nature, see:
Each of the Platonic solids occurs naturally in one form or another:
See also
- List of polygons, all of which have regular forms
- Quasiregular polytope
- Semiregular polytope
- Johnson solid
- Bartel Leendert van der Waerden
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.