Regular icosahedron

The regular icosahedron (or simply icosahedron) is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with regular faces to each of its pentagonal faces, or by putting points onto the cube. The resulting polyhedron has 20 equilateral triangles as its faces, 30 edges, and 12 vertices. It is an example of a Platonic solid and of a deltahedron. The icosahedral graph represents the skeleton of a regular icosahedron.

Regular icosahedron
Type	Deltahedron, Gyroelongated bipyramid, Platonic solid, Regular polyhedron
Faces	20
Edges	30
Vertices	12
Vertex configuration	${\displaystyle 12\times \left(3^{5}\right)}$
Schläfli symbol	${\displaystyle \{3,5\}}$
Symmetry group	icosahedral symmetry ${\displaystyle I_{h}}$
Dihedral angle (degrees)	138.190 (approximately)
Dual polyhedron	regular dodecahedron
Properties	convex, composite, isogonal, isohedral, isotoxal
Net

Many polyhedra are constructed from the regular icosahedron. A notable example is the stellation of regular icosahedron, which consists of 59 polyhedrons. The great dodecahedron, one of the Kepler–Poinsot polyhedra, is constructed by either stellation or faceting. Some of the Johnson solids can be constructed by removing the pentagonal pyramids. The regular icosahedron's dual polyhedron is the regular dodecahedron, and their relation has a historical background on the comparison mensuration. It is analogous to a four-dimensional polytope, the 600-cell.

Regular icosahedrons can be found in nature, a common example is the adenoviruses. Other applications of the regular icosahedron are the usage of its net in cartography, and the twenty-sided dice that may have been used in ancient times but are now commonplace in modern tabletop role-playing games.

Construction

There are several ways to construct a regular icosahedron:

• The construction started from a pentagonal antiprism by attaching two pentagonal pyramids with regular faces to each of its faces.^[1] Such construction led to the regular icosahedron becoming known for composite; the pyramids are the elementary, meaning they cannot be sliced again into smaller convex polyhedrons. This process of construction is known as the gyroelongation, like other polyhedrons in the family of gyroelongated bipyramid. ^[2]

Three mutually perpendicular golden ratio rectangles, with edges connecting their corners, form a regular icosahedron.

• Another way to construct it is by putting two points on each surface of a cube. In each face, draw a segment line between the midpoints of two opposite edges and locate two points with the golden ratio distance from each midpoint. These twelve vertices describe the three mutually perpendicular planes, with edges drawn between each of them.^[3]
• The regular icosahedron can also be constructed starting from a regular octahedron. All triangular faces of a regular octahedron are breaking, twisting at a certain angle, and filling up with other equilateral triangles. This process is known as snub, and the regular icosahedron is also known as snub octahedron.^[4]
• One possible system of Cartesian coordinate for the vertices of a regular icosahedron, given the edge length 2, is: $${\displaystyle \left(0,\pm 1,\pm \varphi \right),\left(\pm 1,\pm \varphi ,0\right),\left(\pm \varphi ,0,\pm 1\right),}$$ where ${\displaystyle \varphi =(1+{\sqrt {5}})/2}$ denotes the golden ratio.^[5]

By the constructions above, the regular icosahedron is Platonic solid, because it has 20 equilateral triangles as it faces. This also results in that regular icosahedron is one of the eight convex deltahedron.^[6] It can be unfolded into 44,380 different nets.^[7]

Properties

Mensuration

The insphere of a convex polyhedron is a sphere inside the polyhedron, touching every face. The circumsphere of a convex polyhedron is a sphere that contains the polyhedron and touches every vertex. The midsphere of a convex polyhedron is a sphere tangent to every edge. Therefore, given that the edge length ${\displaystyle a}$ of a regular icosahedron, the radius of insphere (inradius) ${\displaystyle r_{I}}$, the radius of circumsphere (circumradius) ${\displaystyle r_{C}}$, and the radius of midsphere (midradius) ${\displaystyle r_{M}}$ are, respectively:^[8] $${\displaystyle r_{I}={\frac {\varphi ^{2}a}{2{\sqrt {3}}}}\approx 0.756a,\qquad r_{C}={\frac {\sqrt {\varphi ^{2}+1}}{2}}a\approx 0.951a,\qquad r_{M}={\frac {\varphi }{2}}a\approx 0.809a.}$$

3D model of a regular icosahedron

The surface area of a polyhedron is the sum of the areas of its faces. Therefore, the surface area ${\displaystyle (A)}$ of a regular icosahedron is twenty times that of each of its equilateral triangle faces. The volume ${\displaystyle (V)}$ of a regular icosahedron can be obtained as twenty times that of a pyramid whose base is one of its faces and whose apex is the icosahedron's center; or as the sum of two uniform pentagonal pyramids and a pentagonal antiprism. The expressions of both are:^[9] $${\displaystyle A=5{\sqrt {3}}a^{2}\approx 8.660a^{2},\qquad V={\frac {5\varphi ^{2}}{6}}a^{3}\approx 2.182a^{3}.}$$ A problem dating back to the ancient Greeks is determining which of two shapes has a larger volume, an icosahedron inscribed in a sphere, or a dodecahedron inscribed in the same sphere. The problem was solved by Hero, Pappus, and Fibonacci, among others.^[10] Apollonius of Perga discovered the curious result that the ratio of volumes of these two shapes is the same as the ratio of their surface areas.^[11] Both volumes have formulas involving the golden ratio, but taken to different powers.^[12] As it turns out, the icosahedron occupies less of the sphere's volume (60.54%) than the dodecahedron (66.49%).^[a]

The dihedral angle of a regular icosahedron can be calculated by adding the angle of pentagonal pyramids with regular faces and a pentagonal antiprism. The dihedral angle of a pentagonal antiprism and pentagonal pyramid between two adjacent triangular faces is approximately 38.2°. The dihedral angle of a pentagonal antiprism between pentagon-to-triangle is 100.8°, and the dihedral angle of a pentagonal pyramid between the same faces is 37.4°. Therefore, for the regular icosahedron, the dihedral angle between two adjacent triangles, on the edge where the pentagonal pyramid and pentagonal antiprism are attached is 37.4° + 100.8° = 138.2°.^[13]

Symmetry

Illustration of a icosahedral symmetry. The five-fold, three-fold, and two-fold are labeled in blue, red, and magenta respectively. The mirror planes are the cyan great circle.

The regular icosahedron has six five-fold rotation axes passing through two opposite vertices, ten three-fold axes rotating a triangular face, and fifteen two-fold axes passing through any of its edges. It has fifteen mirror planes as in a cyan great circle on the sphere meeting at order ${\displaystyle \pi /5,\pi /3,\pi /2}$ angles, dividing a sphere into 120 triangles fundamental domains. The full symmetry group of the icosahedron (including reflections) is known as the full icosahedral symmetry ${\displaystyle \mathrm {I} _{\mathrm {h} }}$.^[14] It is isomorphic to the product of the rotational symmetry group and the cyclic group of size two, generated by the reflection through the center of the regular icosahedron.^[15] It shares the dual polyhedron of a regular icosahedron, the regular dodecahedron: a regular icosahedron can be inscribed in a regular dodecahedron by placing its vertices at the face centers of the dodecahedron, and vice versa.^[16]

The rotational symmetry group of the regular icosahedron is isomorphic to the alternating group on five letters. This non-abelian simple group is the only non-trivial normal subgroup of the symmetric group on five letters.^[17] Since the Galois group of the general quintic equation is isomorphic to the symmetric group on five letters, and this normal subgroup is simple and non-abelian, the general quintic equation does not have a solution in radicals. The proof of the Abel–Ruffini theorem uses this simple fact,^[18] and Felix Klein wrote a book that made use of the theory of icosahedral symmetries to derive an analytical solution to the general quintic equation.^[19]

The regular icosahedron, as one of the Platonic solids, is a regular polyhedron. It is isogonal, isohedral, and isotoxal: any two vertices, two faces, and two edges of a regular icosahedron respectively can be transformed by rotations and reflections under its symmetry orbit, which preserves the appearance. Each regular polyhedron has a convex hull on its edge midpoints; icosidodecahedron is the convex hull of a regular icosahedron.^[20] Each vertex is surrounded by five equilateral triangles, so the regular icosahedron denotes ${\displaystyle 3.3.3.3.3}$ in vertex configuration or ${\displaystyle \{3,5\}}$ in Schläfli symbol.^[21]

Icosahedral graph

Icosahedral graph

Every Platonic graph, including the icosahedral graph, is a polyhedral graph. This means that they are planar graphs, graphs that can be drawn in the plane without crossing its edges; and they are 3-vertex-connected, meaning that the removal of any two of its vertices leaves a connected subgraph. According to Steinitz theorem, the icosahedral graph endowed with these heretofore properties represents the skeleton of a regular icosahedron.^[22]

The icosahedral graph has twelve vertices, the same number of vertices as a regular icosahedron. These vertices are connected by five edges from each vertex, making the icosahedral graph 5-regular.^[23] The icosahedral graph is Hamiltonian, because it has a cycle that can visit each vertex exactly once.^[24] Any subset of four vertices has three connected edges, with one being the central of all of those three, and the icosahedral graph has no induced subgraph, a claw-free graph.^[25]

The icosahedral graph is a graceful graph, meaning that each vertex can be labeled with an integer between 0 and 30 inclusive, in such a way that the absolute difference between the labels of an edge's two vertices is different for every edge.^[26]

Related figures

The regular icosahedron has a large number of stellations, constructed by extending the faces of a regular icosahedron. Coxeter et al. (1938) in their work, The Fifty-Nine Icosahedra, identified fifty-nine stellations for the regular icosahedron. The regular icosahedron itself is the zeroth stellation of an icosahedron, and the first stellation has each original face augmented by a low pyramid. The final stellation includes all of the cells in the icosahedron's stellation diagram, meaning every three intersecting face planes of the icosahedral core intersect either on a vertex of this polyhedron or inside it.^[27] The great dodecahedron of Kepler–Poinsot polyhedron is considered part of subsequent stellation.^[28]

The six stellations of the regular icosahedron according to Coxeter et al. (1938): regular icosahedron (zeroth), the first stellation, regular compound of five octahedra, excavated dodecahedron, great icosahedron, and final stellation. See the list for more.

Top left to bottom right: great dodecahedron, truncated icosahedron, triakis icosahedron, and edge-contracted icosahedron

The triakis icosahedron is the Catalan solid constructed by attaching the base of triangular pyramids onto each face of a regular icosahedron, the Kleetope of an icosahedron.^[29] The truncated icosahedron is an Archimedean solid constructed by truncating the vertices of a regular icosahedron; the resulting polyhedron may be considered as a football because of having a pattern of numerous hexagonal and pentagonal faces.^[30]

The great dodecahedron has other ways to construct from the regular icosahedron. Aside from the stellation, the great dodecahedron can be constructed by faceting the regular icosahedron, that is, removing the pentagonal faces of the regular icosahedron without removing the vertices or creating a new one; or forming a regular pentagon by each of the five vertices inside of a regular icosahedron, and twelve regular pentagons intersecting each other, making a pentagram as its vertex figure.^[31]

A Johnson solid is a polyhedron whose faces are all regular but which is not uniform. In other words, they do not include the Archimedean solids, the Catalan solids, the prisms, or the antiprisms. Some Johnson solids can be derived by removing part of a regular icosahedron, a process known as diminishment. They are gyroelongated pentagonal pyramid, metabidiminished icosahedron, and tridiminished icosahedron, which remove one, two, and three pentagonal pyramids from the icosahedron respectively.^[2]

Regular icosahedron and its non-convex variant, which differs from Jessen's icosahedron in having different vertex positions and non-right-angled dihedrals

Another related shape can be derived by keeping the vertices of a regular icosahedron in their original positions and replacing certain pairs of equilateral triangles with pairs of isosceles triangles. The resulting polyhedron has the non-convex version of the regular icosahedron. Nonetheless, it is occasionally incorrectly known as Jessen's icosahedron because of the similar visual, of having the same combinatorial structure and symmetry as Jessen's icosahedron;^[b] the difference is the non-convex one does not form a tensegrity structure and does not have right-angled dihedrals.^[32]

Apart from the construction above, the regular icosahedron can be inscribed in a regular octahedron by placing its twelve vertices on the twelve edges of the octahedron such that they divide each edge in the golden section. Because the resulting segments are unequal, there are five different ways to do this consistently, so five disjoint icosahedra can be inscribed in each octahedron.^[33] Another relation between the two is that they are part of the progressive transformation from the cuboctahedron's rigid struts and flexible vertices, known as jitterbug transformation.^[34]

The edge-contracted icosahedron has a surface like a regular icosahedron but with some faces lie in the same plane.^[35]

The regular icosahedron is analogous to the 600-cell, a regular 4-dimensional polytope.^[36] This polytope has six hundred regular tetrahedra as its cells.^[37]

Appearances

Twenty-sided dice from Ptolemaic of Egypt, inscribed with Greek letters at the faces

The Scattergories twenty-sided die, excluding the six letters Q, U, V, X, Y, and Z

Dice are the most common objects using different polyhedra, one of them being the regular icosahedron. The twenty-sided die was found in many ancient times. One example is the die from the Ptolemaic of Egypt, which later used Greek letters inscribed on the faces in the period of Greece and Rome.^[38] Another example was found in the treasure of Tipu Sultan, which was made out of gold and with numbers written on each face.^[39] In several roleplaying games, such as Dungeons & Dragons, the twenty-sided die (labeled as d20) is commonly used in determining success or failure of an action. It may be numbered from "0" to "9" twice, in which form it usually serves as a ten-sided die (d10); most modern versions are labeled from "1" to "20".^[40] Scattergories is another board game in which the player names the category entires on a card within a given set time. The naming of such categories is initially with the letters contained in every twenty-sided dice.^[41]

The radiolarian Circogonia icosahedra

Dymaxion map, created by the net of a regular icosahedron

The regular icosahedron may also appear in many fields of science as follows:

• In virology, herpes virus have icosahedral shells. The outer protein shell of HIV is enclosed in a regular icosahedron, as is the head of a typical myovirus.^[42] Several species of radiolarians discovered by Ernst Haeckel, described its shells as the like-shaped various regular polyhedra; one of which is Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron.^[43]
• In chemistry, the closo-carboranes are compounds with a shape resembling the regular icosahedron.^[44] The crystal twinning with icosahedral shapes also occurs in crystals, especially nanoparticles.^[45] Many borides and allotropes of boron such as α- and β-rhombohedral contain boron B₁₂ icosahedron as a basic structure unit.^[46]
• In cartography, R. Buckminster Fuller used the net of a regular icosahedron to create a map known as Dymaxion map, by subdividing the net into triangles, followed by calculating the grid on the Earth's surface, and transferring the results from the sphere to the polyhedron. This projection was created during the time that Fuller realized that the Greenland is smaller than South America.^[47]
• In the Thomson problem, concerning the minimum-energy configuration of ${\displaystyle n}$ charged particles on a sphere, and for the Tammes problem of constructing a spherical code maximizing the smallest distance among the points, the minimum solution known for ${\displaystyle n=12}$ places the points at the vertices of a regular icosahedron, inscribed in a sphere. This configuration is proven optimal for the Tammes problem, but a rigorous solution to this instance of the Thomson problem is unknown.^[48]

Sketch of a regular icosahedron by Johannes Kepler

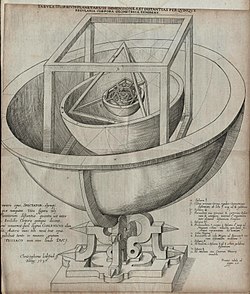
Kepler's Platonic solid model of the Solar System

As mentioned above, the regular icosahedron is one of the five Platonic solids. The regular polyhedra have been known since antiquity, but are named after Plato who, in his Timaeus dialogue, identified these with the five elements, whose elementary units were attributed these shapes: fire (tetrahedron), air (octahedron), water (icosahedron), earth (cube) and the shape of the universe as a whole (dodecahedron). Euclid's Elements defined the Platonic solids and solved the problem of finding the ratio of the circumscribed sphere's diameter to the edge length.^[49] Following their identification with the elements by Plato, Johannes Kepler in his Harmonices Mundi sketched each of them, in particular, the regular icosahedron.^[50] In his Mysterium Cosmographicum, he also proposed a model of the Solar System based on the placement of Platonic solids in a concentric sequence of increasing radius of the inscribed and circumscribed spheres whose radii gave the distance of the six known planets from the common center. The ordering of the solids, from innermost to outermost, consisted of: regular octahedron, regular icosahedron, regular dodecahedron, regular tetrahedron, and cube.^[51]