Top Qs
Timeline
Chat
Perspective
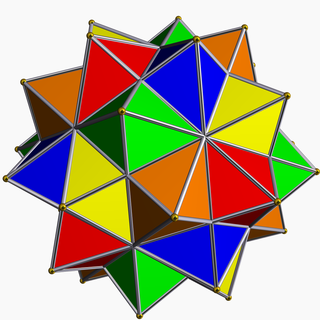
Compound of five octahedra
Polyhedral compound From Wikipedia, the free encyclopedia
Remove ads
The compound of five octahedra is one of the five regular polyhedron compounds, and can also be seen as a stellation. It was first described by Edmund Hess in 1876. It is unique among the regular compounds for not having a regular convex hull.
| Compound of five octahedra | |
|---|---|
(see here for a 3D model) | |
| Type | Regular compound |
| Index | UC17, W23 |
| Coxeter symbol | [5{3,4}]2{3,5}[1] |
| Elements (As a compound) | 5 octahedra: F = 40, E = 60, V = 30 |
| Dual compound | Compound of five cubes |
| Symmetry group | icosahedral (Ih) |
| Subgroup restricting to one constituent | pyritohedral (Th) |
Remove ads
As a stellation
It is the second stellation of the icosahedron, and given as Wenninger model index 23.
It can be constructed by a rhombic triacontahedron with rhombic-based pyramids added to all the faces, as shown by the five colored model image. (This construction does not generate the regular compound of five octahedra, but shares the same topology and can be smoothly deformed into the regular compound.)
It has a density of greater than 1.
Remove ads
As a compound
It can also be seen as a polyhedral compound of five octahedra arranged in icosahedral symmetry (Ih).
The spherical and stereographic projections of this compound look the same as those of the disdyakis triacontahedron.
But the convex solid's vertices on 3- and 5-fold symmetry axes (gray in the images below) correspond only to edge crossings in the compound.
Replacing the octahedra by tetrahemihexahedra leads to the compound of five tetrahemihexahedra.
Remove ads
Other 5-octahedra compounds
A second 5-octahedra compound, with octahedral symmetry, also exists. It can be generated by adding a fifth octahedron to the standard 4-octahedra compound.
See also
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads