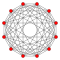
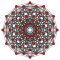
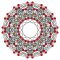
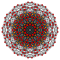
Runcinated 6-cubes

In six-dimensional geometry, a runcinated 6-cube is a convex uniform 6-polytope with 3rd order truncations (runcination) of the regular 6-cube.

6-cube	Runcinated 6-cube	Biruncinated 6-cube	Runcinated 6-orthoplex	6-orthoplex
Runcitruncated 6-cube	Biruncitruncated 6-cube	Runcicantellated 6-orthoplex	Runcicantellated 6-cube	Biruncitruncated 6-orthoplex
Runcitruncated 6-orthoplex	Runcicanti-truncated 6-cube	Biruncicanti-truncated 6-cube	Runcicanti-truncated 6-orthoplex
Orthogonal projections in B6 Coxeter plane

There are 12 unique runcinations of the 6-cube with permutations of truncations, and cantellations. Half are expressed relative to the dual 6-orthoplex.

Runcinated 6-cube

Runcinated 6-cube
Type	Uniform 6-polytope
Schläfli symbol	t0,3{4,3,3,3,3}
Coxeter-Dynkin diagram
4-faces
Cells
Faces
Edges	7680
Vertices	1280
Vertex figure
Coxeter group	B6 [4,3,3,3,3]
Properties	convex

Alternate names

• Small prismated hexeract (spox) (Jonathan Bowers)^[1]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Biruncinated 6-cube

Biruncinated 6-cube
Type	Uniform 6-polytope
Schläfli symbol	t1,4{4,3,3,3,3}
Coxeter-Dynkin diagram
4-faces
Cells
Faces
Edges	11520
Vertices	1920
Vertex figure
Coxeter group	B6 [4,3,3,3,3]
Properties	convex

Alternate names

• Small biprismated hexeractihexacontatetrapeton (sobpoxog) (Jonathan Bowers)^[2]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Runcitruncated 6-cube

Runcitruncated 6-cube
Type	Uniform 6-polytope
Schläfli symbol	t0,1,3{4,3,3,3,3}
Coxeter-Dynkin diagram
4-faces
Cells
Faces
Edges	17280
Vertices	3840
Vertex figure
Coxeter group	B6 [4,3,3,3,3]
Properties	convex

Alternate names

• Prismatotruncated hexeract (potax) (Jonathan Bowers)^[3]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Biruncitruncated 6-cube

Biruncitruncated 6-cube
Type	Uniform 6-polytope
Schläfli symbol	t1,2,4{4,3,3,3,3}
Coxeter-Dynkin diagram
4-faces
Cells
Faces
Edges	23040
Vertices	5760
Vertex figure
Coxeter group	B6 [4,3,3,3,3]
Properties	convex

Alternate names

• Biprismatotruncated hexeract (boprag) (Jonathan Bowers)^[4]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Runcicantellated 6-cube

Runcicantellated 6-cube
Type	Uniform 6-polytope
Schläfli symbol	t0,2,3{4,3,3,3,3}
Coxeter-Dynkin diagram
4-faces
Cells
Faces
Edges	13440
Vertices	3840
Vertex figure
Coxeter group	B6 [4,3,3,3,3]
Properties	convex

Alternate names

• Prismatorhombated hexeract (prox) (Jonathan Bowers)^[5]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Runcicantitruncated 6-cube

Runcicantitruncated 6-cube
Type	Uniform 6-polytope
Schläfli symbol	t0,1,2,3{4,3,3,3,3}
Coxeter-Dynkin diagram
4-faces
Cells
Faces
Edges	23040
Vertices	7680
Vertex figure
Coxeter group	B6 [4,3,3,3,3]
Properties	convex

Alternate names

• Great prismated hexeract (gippox) (Jonathan Bowers)^[6]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Biruncitruncated 6-cube

Biruncitruncated 6-cube
Type	Uniform 6-polytope
Schläfli symbol	t1,2,3,4{4,3,3,3,3}
Coxeter-Dynkin diagram
4-faces
Cells
Faces
Edges	23040
Vertices	5760
Vertex figure
Coxeter group	B6 [4,3,3,3,3]
Properties	convex

Alternate names

• Biprismatotruncated hexeract (boprag) (Jonathan Bowers)^[7]

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Related polytopes

These polytopes are from a set of 63 uniform 6-polytopes generated from the B₆ Coxeter plane, including the regular 6-cube or 6-orthoplex.

B6 polytopes
β6	t1β6	t2β6	t2γ6	t1γ6	γ6	t0,1β6	t0,2β6
t1,2β6	t0,3β6	t1,3β6	t2,3γ6	t0,4β6	t1,4γ6	t1,3γ6	t1,2γ6
t0,5γ6	t0,4γ6	t0,3γ6	t0,2γ6	t0,1γ6	t0,1,2β6	t0,1,3β6	t0,2,3β6
t1,2,3β6	t0,1,4β6	t0,2,4β6	t1,2,4β6	t0,3,4β6	t1,2,4γ6	t1,2,3γ6	t0,1,5β6
t0,2,5β6	t0,3,4γ6	t0,2,5γ6	t0,2,4γ6	t0,2,3γ6	t0,1,5γ6	t0,1,4γ6	t0,1,3γ6
t0,1,2γ6	t0,1,2,3β6	t0,1,2,4β6	t0,1,3,4β6	t0,2,3,4β6	t1,2,3,4γ6	t0,1,2,5β6	t0,1,3,5β6
t0,2,3,5γ6	t0,2,3,4γ6	t0,1,4,5γ6	t0,1,3,5γ6	t0,1,3,4γ6	t0,1,2,5γ6	t0,1,2,4γ6	t0,1,2,3γ6
t0,1,2,3,4β6	t0,1,2,3,5β6	t0,1,2,4,5β6	t0,1,2,4,5γ6	t0,1,2,3,5γ6	t0,1,2,3,4γ6	t0,1,2,3,4,5γ6