A6 polytope

In 6-dimensional geometry, there are 35 uniform polytopes with A₆ symmetry. There is one self-dual regular form, the 6-simplex with 7 vertices.

Orthographic projections
A₆ Coxeter plane

6-simplex

Each can be visualized as symmetric orthographic projections in Coxeter planes of the A₆ Coxeter group, and other subgroups.

Graphs

Symmetric orthographic projections of these 35 polytopes can be made in the A₆, A₅, A₄, A₃, A₂ Coxeter planes. A_k graphs have [k+1] symmetry. For even k and symmetric ringed diagrams, symmetry doubles to [2(k+1)].

These 35 polytopes are each shown in these 5 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.

#	A6 [7]	A5 [6]	A4 [5]	A3 [4]	A2 [3]	Coxeter-Dynkin diagram Schläfli symbol Name
1						t0{3,3,3,3,3} 6-simplex Heptapeton (hop)
2				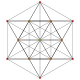		t1{3,3,3,3,3} Rectified 6-simplex Rectified heptapeton (ril)
3						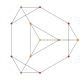t0,1{3,3,3,3,3} Truncated 6-simplex Truncated heptapeton (til)
4						t2{3,3,3,3,3} Birectified 6-simplex Birectified heptapeton (bril)
5						t0,2{3,3,3,3,3} Cantellated 6-simplex Small rhombated heptapeton (sril)
6						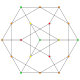t1,2{3,3,3,3,3} Bitruncated 6-simplex Bitruncated heptapeton (batal)
7						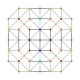t0,1,2{3,3,3,3,3} Cantitruncated 6-simplex Great rhombated heptapeton (gril)
8						t0,3{3,3,3,3,3} Runcinated 6-simplex Small prismated heptapeton (spil)
9				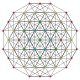		t1,3{3,3,3,3,3} Bicantellated 6-simplex Small birhombated heptapeton (sabril)
10				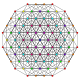		t0,1,3{3,3,3,3,3} Runcitruncated 6-simplex Prismatotruncated heptapeton (patal)
11						t2,3{3,3,3,3,3} Tritruncated 6-simplex Tetradecapeton (fe)
12						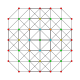t0,2,3{3,3,3,3,3} Runcicantellated 6-simplex Prismatorhombated heptapeton (pril)
13						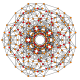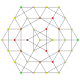t1,2,3{3,3,3,3,3} Bicantitruncated 6-simplex Great birhombated heptapeton (gabril)
14				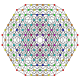		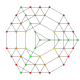t0,1,2,3{3,3,3,3,3} Runcicantitruncated 6-simplex Great prismated heptapeton (gapil)
15						t0,4{3,3,3,3,3} Stericated 6-simplex Small cellated heptapeton (scal)
16				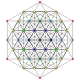		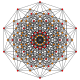t1,4{3,3,3,3,3} Biruncinated 6-simplex Small biprismato-tetradecapeton (sibpof)
17						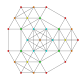t0,1,4{3,3,3,3,3} Steritruncated 6-simplex cellitruncated heptapeton (catal)
18						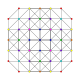t0,2,4{3,3,3,3,3} Stericantellated 6-simplex Cellirhombated heptapeton (cral)
19						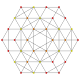t1,2,4{3,3,3,3,3} Biruncitruncated 6-simplex Biprismatorhombated heptapeton (bapril)
20						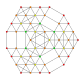t0,1,2,4{3,3,3,3,3} Stericantitruncated 6-simplex Celligreatorhombated heptapeton (cagral)
21						t0,3,4{3,3,3,3,3} Steriruncinated 6-simplex Celliprismated heptapeton (copal)
22						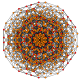t0,1,3,4{3,3,3,3,3} Steriruncitruncated 6-simplex celliprismatotruncated heptapeton (captal)
23						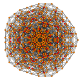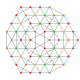t0,2,3,4{3,3,3,3,3} Steriruncicantellated 6-simplex celliprismatorhombated heptapeton (copril)
24						t1,2,3,4{3,3,3,3,3} Biruncicantitruncated 6-simplex Great biprismato-tetradecapeton (gibpof)
25				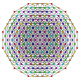		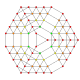t0,1,2,3,4{3,3,3,3,3} Steriruncicantitruncated 6-simplex Great cellated heptapeton (gacal)
26						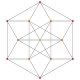t0,5{3,3,3,3,3} Pentellated 6-simplex Small teri-tetradecapeton (staf)
27						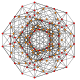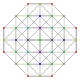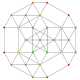t0,1,5{3,3,3,3,3} Pentitruncated 6-simplex Tericellated heptapeton (tocal)
28						t0,2,5{3,3,3,3,3} Penticantellated 6-simplex Teriprismated heptapeton (tapal)
29						t0,1,2,5{3,3,3,3,3} Penticantitruncated 6-simplex Terigreatorhombated heptapeton (togral)
30				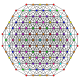		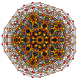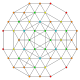t0,1,3,5{3,3,3,3,3} Pentiruncitruncated 6-simplex Tericellirhombated heptapeton (tocral)
31						t0,2,3,5{3,3,3,3,3} Pentiruncicantellated 6-simplex Teriprismatorhombi-tetradecapeton (taporf)
32						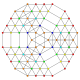t0,1,2,3,5{3,3,3,3,3} Pentiruncicantitruncated 6-simplex Terigreatoprismated heptapeton (tagopal)
33						t0,1,4,5{3,3,3,3,3} Pentisteritruncated 6-simplex tericellitrunki-tetradecapeton (tactaf)
34						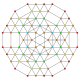t0,1,2,4,5{3,3,3,3,3} Pentistericantitruncated 6-simplex tericelligreatorhombated heptapeton (tacogral)
35						t0,1,2,3,4,5{3,3,3,3,3} Omnitruncated 6-simplex Great teri-tetradecapeton (gotaf)

References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 ^[1]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

External links

• Klitzing, Richard. "6D uniform polytopes (polypeta)".