Relation (Mathematik)

Eine Relation (lateinisch relatio „Beziehung“, „Verhältnis“) ist allgemein eine Beziehung, die zwischen Dingen bestehen kann. Bei Relationen im Sinne der Mathematik ist stets klar, ob sie bestehen oder nicht, sodass Objekte nicht „bis zu einem gewissen Grade“ in einer Relation zueinander stehen. Damit ist eine einfache mengentheoretische Definition des Begriffs möglich: Eine Relation ${\displaystyle R}$ ist eine Menge von ${\displaystyle n}$-Tupeln. In der Relation ${\displaystyle R}$ zueinander stehende Dinge bilden ${\displaystyle n}$-Tupel, die Element von ${\displaystyle R}$ sind.

Wird nicht ausdrücklich etwas anderes angegeben, versteht man unter einer Relation gemeinhin eine zweistellige oder binäre Relation. Bei einer solchen Beziehung bilden dann jeweils zwei Elemente ${\displaystyle a}$ und ${\displaystyle b}$ ein geordnetes Paar ${\displaystyle (a,b).}$ Stammen dabei ${\displaystyle a}$ und ${\displaystyle b}$ aus verschiedenen Grundmengen ${\displaystyle A}$ und ${\displaystyle B}$, so heißt die Relation heterogen oder „Relation zwischen den Mengen ${\displaystyle A}$ und ${\displaystyle B}$.“ Stimmen die Grundmengen überein (${\displaystyle A=B}$), dann heißt die Relation homogen oder „Relation in bzw. auf der Menge ${\displaystyle A}$.“

Wichtige Spezialfälle, zum Beispiel Äquivalenzrelationen und Ordnungsrelationen, sind Relationen auf einer Menge.

Heute sehen manche Autoren den Begriff Relation nicht unbedingt als auf Mengen beschränkt an, sondern lassen jede aus geordneten Paaren bestehende Klasse als Relation gelten.

Definitionen

Zweistellige Relation

Eine zweistellige Relation ${\displaystyle R}$ (auch binäre Relation genannt)^[1] zwischen zwei Mengen ${\displaystyle A}$ und ${\displaystyle B}$ ist eine Teilmenge des kartesischen Produkts ${\displaystyle A\times B=\{(a,b)\mid a\in A,b\in B\}\colon }$^[2][3][4]

${\displaystyle R\subseteq A\times B}$.

Die Menge ${\displaystyle A}$ wird als Quellmenge (englisch: set of departure) der Relation ${\displaystyle R}$ bezeichnet, die Menge ${\displaystyle B}$ als Zielmenge (englisch: set of destination).^[5]

Manchmal ist diese Definition jedoch nicht präzise genug und man bezieht die Quell- und Zielmenge in die Definition mit ein, obige Teilmenge wird dann der Graph ${\displaystyle G_{R}}$ der Relation genannt. Eine zweistellige Relation ${\displaystyle R}$ ist dann definiert als Tripel

${\displaystyle R=(G_{R},A,B)}$ mit ${\displaystyle G_{R}\equiv \operatorname {Graph} (R)\subseteq A\times B}$.

Die Kenntnis von Quelle und Zielmenge ist insbesondere dann von Bedeutung, wenn man Funktionen als spezielle (sogenannte funktionale) Relationen betrachtet.

Als Urbild-, Argument- oder Definitions- oder Vorbereich^[6][7] einer gegebenen zweistelligen Relation ${\displaystyle R}$ wird der kleinstmögliche Vorbereich zum Graphen ${\displaystyle G_{R}}$ verstanden, dessen Elemente alle in den geordneten Paaren von ${\displaystyle R}$ tatsächlich auf der linken Seite auftreten, in Zeichen

${\displaystyle Db(R)\equiv {\mathfrak {D}}(R):=\{a\mid \exists b\colon (a,b)\in G_{R}\}\subseteq A}$.^[8][9][10]

Der Wertevorrat, Werte- oder Bild- oder Nachbereich^[6][7] bezeichnet in diesem Sinne den kleinsten Nachbereich zu ${\displaystyle G_{R}}$ bei gegebenem ${\displaystyle R}$, dessen Elemente also alle in den Paaren von ${\displaystyle R}$ auf der rechten Seite auftreten, in Zeichen

${\displaystyle Wb(R)\equiv {\mathfrak {B}}(R):=\{b\mid \exists a\colon (a,b)\in G_{R}\}\subseteq B}$.^[11][9][12]

Gelegentlich wird für die Vereinigungsmenge die Bezeichnung Feld (oder Knotenmenge) benutzt, in Zeichen

${\displaystyle Fd(R)\equiv {\mathfrak {F}}(R):=Db(R)\cup Wb(R)=\{x\mid \exists x'\colon (x,x')\in G_{R}\lor (x',x)\in R\}\subseteq A\cup B}$.^[13][9]

Darüber hinaus finden sich folgende Bezeichnungen:

• Domäne (englisch domain) ${\displaystyle \operatorname {dom} R}$ entweder für die (im Prinzip beliebig große) Quellmenge oder für die (durch den Graphen festgelegte) Urbildmenge (Definitionsbereich),
• Co-Domäne (englisch codomain, range) ${\displaystyle \operatorname {cod} R,\operatorname {ran} R}$ entweder für die Zielmenge oder für die Bildmenge,^[14]
• Knotenmenge (${\displaystyle \operatorname {ver} R}$) für das Feld^[1] einer Relation.

Stimmen zwei Relationen in ihren Graphen überein, so sagt man auch, sie seien im Wesentlichen gleich.
Beispiel: Jede Relation ${\displaystyle R=(G_{R},A,B)}$ ist im Wesentlichen gleich mit ${\displaystyle (G_{R},Db(R),Wb(R))}$ und mit der homogenen Relation ${\displaystyle (G_{R},Fd(R),Fd(R))}$.

n-stellige Relation

Allgemeiner ist eine ${\displaystyle n}$-stellige Relation ${\displaystyle R}$ eine Teilmenge des kartesischen Produkts von ${\displaystyle n}$ Mengen ${\displaystyle A_{1},\dotsc ,A_{n}}$:

${\displaystyle R\subseteq A_{1}\times \dotsb \times A_{n}}$ mit ${\displaystyle A_{1}\times \dotsb \times A_{n}=\{(a_{1},\dotsc ,a_{n})\mid a_{1}\in A_{1},\dotsc ,a_{n}\in A_{n}\}}$.

Dabei bezeichnet ${\displaystyle A=(A_{i})_{i\in \{1,\dots n\}}}$ die endliche Folge der Mengen, und ${\displaystyle \textstyle \prod A=\textstyle \prod _{i=1}^{n}A_{i}}$ das kartesische Produkt.

Die ausführlichere Definition lässt sich auch auf ${\displaystyle n}$-stellige Relationen verallgemeinern und man erhält dann das ${\displaystyle (n+1)}$-Tupel

${\displaystyle R=(G_{R},A_{1},\dotsc ,A_{n})=(G_{R},A)}$ mit ${\displaystyle G_{R}\equiv \operatorname {Graph} (R)\subseteq A_{1}\times \dotsb \times A_{n}=\textstyle \prod A}$.

Die Mengen ${\displaystyle A_{1},\dotsc ,A_{i},\dotsc ,A_{n}}$ heißen Trägermengen der Relation mit den minimalen Trägermengen zum Graphen ${\displaystyle G_{R}}$, nämlich

${\displaystyle Tr_{i}(R)\equiv {\mathfrak {T}}_{i}(R):=\{a_{i}\mid \exists a_{1},\dotsc ,a_{i-1},a_{i+1},\dotsc ,a_{n}\colon (a_{1},\dotsc ,a_{i-1},a_{i},a_{i+1},\dotsc ,a_{n})\in G_{R}\}}$.

Das Feld einer ${\displaystyle n}$-stelligen Relation ist gegeben durch

${\displaystyle Fd(R)\equiv {\mathfrak {F}}(R):=\textstyle \bigcup \{Tr_{i}(R)\mid 1\leq i\leq n\}\subseteq \textstyle \bigcup A}$.

Wesentliche Gleichheit ist analog definiert wie für zweistellige Relationen durch Übereinstimmung der Graphen, insbesondere ist jede ${\displaystyle n}$-stellige Relation ${\displaystyle R=(G_{R},A_{1},\dotsc ,A_{n})}$ im Wesentlichen gleich mit ${\displaystyle (G_{R},Tr_{1}(R),\dotsc ,Tr_{n}(R))}$ und mit der homogenen Relation ${\displaystyle (G_{R},\underbrace {Fd(R),\dotsc ,Fd(R)} _{n{\text{-mal}}})}$.

Einstellige und nullstellige Relation

Eine einstellige Relation auf einer Menge ${\displaystyle A}$ ist somit einfach eine Teilmenge ${\displaystyle R\subseteq A}$, in der ausführlichen Definition ${\displaystyle R=(G_{R},A)}$ mit ${\displaystyle G_{R}\subseteq A}$.

Die nullstelligen Relationen sind demnach die Teilmengen des leeren kartesischen Produkts ${\displaystyle \textstyle \prod _{i=1}^{0}A_{i}=\{\emptyset \}}$ bzw. ${\displaystyle A^{0}=\{\emptyset \}}$, also ${\displaystyle \emptyset }$ und ${\displaystyle \{\emptyset \}}$, ausführlich ${\displaystyle (\emptyset ,\{\emptyset \})}$ und ${\displaystyle (\{\emptyset \},\{\emptyset \})}$.

Relationen zwischen oder auf echten Klassen

Häufig sind die Trägerbereiche ${\displaystyle A_{i}}$ einer Relation keine Mengen, sondern echte Klassen, man spricht dann von Klassenrelationen. Gelegentlich kann man mengentheoretische Probleme, die sich daraus ergeben, vermeiden, indem man nur noch den Graph der entsprechenden Relation betrachtet. Die (minimalen) Trägermengen (${\displaystyle Tr_{i}(R)}$, im zweistelligen Fall Definitions- und Wertemenge ${\displaystyle Db(R),Wb(R)}$) sind tatsächlich Mengen, aber es ist nicht nötig, sich von vornherein auf Quellmenge, Zielmenge, … (${\displaystyle A,B,A_{i},\dotsc }$) festzulegen, wenn die Relationen im Wesentlichen gleich sind. Nicht immer ist das möglich, beispielsweise für die Äquivalenzrelation der Gleichmächtigkeit, siehe auch: Kardinalzahlen §Definition. Gleichheit von Relationen im Wesentlichen ist ein weiteres Beispiel.

Eine zweistellige Klassenrelation ${\displaystyle R}$ mit Quellklasse ${\displaystyle A}$ und Zielklasse ${\displaystyle B}$ heißt vorgängerklein,^[15][16] wenn für alle ${\displaystyle b\in B}$ die Klasse der Vorgänger ${\displaystyle \{a\in A\mid aRb\}}$ (Urbildfaser von ${\displaystyle b}$, s. u.) eine Menge (d. h. keine echte Klasse) ist.^[17] Die Relation heißt englisch right-narrow (deutsch in etwa nachfolgerklein),^[18] wenn für alle ${\displaystyle a\in A}$ die Klasse der Nachfolger ${\displaystyle \{b\in B\mid aRb\}}$ (Bildfaser von ${\displaystyle a}$) eine Menge ist. Im Fall der Rechtseindeutigkeit (partielle Abbildungen, Abbildungen, s. u.) ist eine Klassenrelation stets klein, da es zu jedem Urbild (genau oder höchstens) einen Bildwert gibt, die Klasse der Nachfolger also eine Einermenge (oder die Leermenge) ist. Jede injektive Klassenabbildung ist beides, klein und vorgängerklein. Die Enthaltenseinsrelation ${\displaystyle \in }$ ist für jede Klasse ${\displaystyle B}$ vorgängerklein, da die ${\displaystyle b\in B}$ keine echten Klassen sein können, sondern Mengen sind und damit ${\displaystyle \{a\in A\mid a\in b\}\subseteq b}$ ebenfalls eine Menge ist.^[19][20] Die Begriffe Vorgänger und Nachfolger selbst werden üblicherweise im Kontext von Ordnungsrelationen verwendet, siehe Ordnungsrelation §Vorgänger und Nachfolger.

Erläuterungen und Schreibweisen

Das kartesische Produkt zweier Mengen ${\displaystyle A}$ und ${\displaystyle B}$ ist die Menge aller geordneten Paare von ${\displaystyle a}$ und ${\displaystyle b,}$ wobei ${\displaystyle a}$ irgendein Element aus der Menge ${\displaystyle A}$ und ${\displaystyle b}$ eines aus ${\displaystyle B}$ darstellt. Bei dem geordneten Paar ist die Reihenfolge wichtig, d. h. ${\displaystyle (a,b)}$ unterscheidet sich von ${\displaystyle (b,a),}$ im Gegensatz zum ungeordneten Paar ${\displaystyle \{a,b\},}$ das identisch ist mit ${\displaystyle \{b,a\}.}$ Für ${\displaystyle (a,b)\in R}$ schreibt man auch ${\displaystyle a\;R\;b,}$, um zu verdeutlichen, dass jene Beziehung zwischen den Objekten besteht (wie in ${\displaystyle a>b}$). Die Leermenge als Teilmenge des kartesischen Mengenprodukts als Relation aufgefasst heißt Nullrelation ${\displaystyle \mathrm {O}$ :=\emptyset =\{\}} , das volle Produkt heißt Allrelation (auch Universalrelation) ${\displaystyle \mathrm {U} }$ (auch als ${\displaystyle \nabla }$ bezeichnet).^[21]

Relationen und Funktionen

• Eine Funktion ${\displaystyle f\colon A\to B}$ ist eine spezielle, nämlich eine linkstotale und rechtseindeutige (zweistellige) Relation, näheres siehe unten.
• Eine Multifunktion ${\displaystyle f\colon X\multimap Y}$ ist eine linkstotale Relation ${\displaystyle f\subseteq A\times B}$.
• Eine partielle Funktion ${\displaystyle f\colon \;X\rightharpoonup Y}$ ist eine (im Allgemeinen nicht linkstotale) rechtseindeutige Relation ${\displaystyle f\subseteq A\times B}$.

In allen Fällen ist ${\displaystyle f\subseteq A\times B}$ (beziehungsweise ${\displaystyle G_{f}\subseteq A\times B}$ wenn die ausführliche Definition zugrunde gelegt wird).

Für Funktionen und Multifunktionen gilt:

Bei der ausführlicheren Definition ${\displaystyle f=(G_{f},A,B)}$ kann, weil ${\displaystyle A}$ durch ${\displaystyle G_{f}}$ eindeutig bestimmt ist (linkstotal), auch ${\displaystyle A}$ weggelassen und einfacher ${\displaystyle f=(G_{f},B)}$ genommen werden.

Für Funktionen und partielle Funktionen gilt:

Für ${\displaystyle (a,b)\in f}$ bzw. ${\displaystyle (a,b)\in G_{f}}$ wird auch ${\displaystyle f\colon a\mapsto b}$ (englisch: maplet), oder ${\displaystyle f(a)=b}$ geschrieben.

Allgemein gilt:

1. Die nullstelligen Relationen ${\displaystyle \mathrm {O} =\emptyset }$ (als nullstellige Nullrelation) und ${\displaystyle \mathrm {U} =\{\emptyset \}}$ (als nullstellige Vollrelation) haben als charakteristische Funktionen die booleschen oder logischen Konstanten ${\displaystyle {\mathsf {falsch}}}$ und ${\displaystyle {\mathsf {wahr}}}$, wie immer für Nullrelation und Allrelation.^[22]
2. Der Fall einstelliger Relationen ist trivial.
3. Eine Relation ${\displaystyle R\subseteq A\times B}$ (bzw. ${\displaystyle R=(G_{R},A,B)}$) entspricht auf eindeutige Weise einer Wahrheitsfunktion ${\displaystyle \chi _{R}\colon \;A\times B\to \{{\mathsf {wahr}},{\mathsf {falsch}}\}}$. Diese Funktion ist auch als Indikatorfunktion oder charakteristische Funktion der Teilmenge ${\displaystyle R\subseteq A\times B}$ (bzw. ${\displaystyle G_{R}\subseteq A\times B}$) bekannt, wobei ${\displaystyle \{{\mathsf {wahr}},{\mathsf {falsch}}\}}$ durch ${\displaystyle \{1,0\}}$ ersetzbar ist.
4. Eine ${\displaystyle n}$-stellige Relation ${\displaystyle R\subseteq A_{1}\times \dotsb \times A_{n}}$ (bzw. ${\displaystyle R=(G_{R},A_{1},\dotsc ,A_{n})}$) entspricht der charakteristischen Funktion ${\displaystyle \chi _{R}\colon A_{1}\times \dotsb \times A_{n}\to \{{\mathsf {wahr}},{\mathsf {falsch}}\}.}$

Es gilt:

• ${\displaystyle n=0\colon \;\chi _{\emptyset }\Leftrightarrow {\mathsf {falsch}},\chi _{\{\emptyset \}}\Leftrightarrow {\mathsf {wahr}}}$.

${\displaystyle n=1\colon \;\chi _{R}(a)\Leftrightarrow a\in R}$.

${\displaystyle n=2\colon \;\chi _{R}(a,b)\Leftrightarrow aRb\Leftrightarrow (a,b)\in R}$.

${\displaystyle n>2\colon \;\chi _{R}(a_{1},\dotsc ,a_{n})\Leftrightarrow (a_{1},\dotsc ,a_{n})\in R}$.^[23]

• Eine Relation ${\displaystyle R\subseteq A\times B}$ lässt sich ebenso als eine Abbildung ${\displaystyle \kappa _{R}}$ von ${\displaystyle A}$ in die Potenzmenge von ${\displaystyle B}$ auffassen, ${\displaystyle \kappa _{R}\colon A\to {\mathcal {P}}(B),\;a\mapsto \{b\in B\mid (a,b)\in R\},}$ man spricht dann oft von einer Korrespondenz, und für ${\displaystyle B=A}$ von einer Transitionsrelation.

Verkettung von Relationen

Die Vorwärtsverkettung^[24] zweier zweistelliger Relationen ${\displaystyle R\subseteq A\times B,S\subseteq C\times D}$ ist wie folgt definiert:

${\displaystyle {\begin{array}{lll}R\;\mathbf {;} \;S\equiv RS&:=\{(a,d)\mid \exists b\colon \;aRb\land bSd\}\\&=\{(a,d)\in A\times D\mid \exists b\in B\cap C\colon \;(a,b)\in R\land (b,d)\in S\}.\end{array}}}$^[25][26][27]

Die Verkettung in der umgekehrten Reihenfolge wird als Rückwärtsverkettung^[28] bezeichnet:

${\displaystyle S\circ R\qquad \quad$ :=\{(a,d)\in A\times D\mid \exists b\in B\cap C\colon \;(a,b)\in R\land (b,d)\in S\}=R\;\mathbf {;} \;S} .^[26][29]

Manche Autoren (W. v. O. Quine) verwenden hierfür alternativ die Notation ${\displaystyle S\mid R}$.^[30]

Die Reihenfolge ist bei der Rückwärtsverkettung dieselbe wie bei der Verkettung von Funktionen (die als spezielle Relationen aufgefasst werden können).

Die Verkettung zweistelliger Relationen wird auch als relatives Produkt bezeichnet. Bei der Verkettung kann auch die einfachste Relation, die in jedem kartesischen Produkt enthaltene leere Relation ${\displaystyle \emptyset }$ (leere Menge) auftreten, nämlich wenn ${\displaystyle B}$ und ${\displaystyle C}$ disjunkt sind, in Zeichen: ${\displaystyle B\cap C=\emptyset }$.

Beispiel: Die Relation „Schwägerin sein von“ ist die Vereinigungsmenge

• des relativen Produktes der Relation „Bruder sein von“ und der Relation „Ehefrau sein von“ und
• des relativen Produktes der Relation „Ehepartner(in) sein von“ und der Relation „Schwester sein von“.

Umkehrrelation

Die Umkehrrelation (auch konverse Relation, Konverse oder inverse Relation genannt) ist für eine zweistellige Relation ${\displaystyle R\subseteq A\times B}$ definiert als

${\displaystyle {\overset {\smallsmile }{R}}\equiv {}^{\smallsmile }{R}\equiv R^{\sim }\equiv R^{-1}:=\{(b,a)\in B\times A\mid (a,b)\in R\}}$.^[30][26]

Gelegentlich findet sich hierfür auch die Bezeichnung transponierte Relation, in Zeichen ${\displaystyle R^{T}}$.^[31]

• Beispiel 1: Die Umkehrrelation der Relation „ist Nachkomme von“ ist die Relation „ist Vorfahre von“.
• Beispiel 2: Die Umkehrrelation der Relation „ist kleiner als“ ist die Relation „ist größer als“.
• Beispiel 3: Die Umkehrrelation der Relation „liefert an“ ist die Relation „wird beliefert von“.

Die Verallgemeinerung der Umkehrrelation (Konverse) auf ${\displaystyle n}$-stellige Relationen ist die Permutation der Koordinaten der in ihr enthaltenen ${\displaystyle n}$-Tupel, speziell

• die Vertauschungen von lediglich 2 Koordinaten (Transpositionen) und
• die Umkehrung der Reihenfolge (Spiegelung),

beides Beispiele (zyklischer) selbstinverser Permutationen.

Sei ${\displaystyle \pi \colon \{1,2,\dotsc ,n\}\rightarrow \{1,2,\dotsc ,n\}}$ eine Permutation (d. h. eine bijektive Abbildung von ${\displaystyle \{1,\dotsc ,n\}}$ auf sich selbst),^[32] und sei ${\displaystyle R\subseteq (A_{i})_{i\in \{1,\dotsc ,n\}}}$ eine ${\displaystyle n}$-stellige Relation, dann ist ${\displaystyle S:=\{a\circ \pi \mid a\in R\}}$ die nach Anwenden der Permutation ${\displaystyle \pi }$ sich ergebende Relation (man verstehe ${\displaystyle a=(a_{i})_{i\in \{1,\dotsc ,n\}}}$ als Familie). Im Fall der Spiegelung

${\displaystyle \pi =\sigma _{n}={\begin{pmatrix}1&2&\cdots &n\\n&n-1&\cdots &1\end{pmatrix}}}$

ist ${\displaystyle S=\{(a_{n},\dotsc ,a_{1})\mid (a_{1},\dotsc ,a_{n})\in R\}}$.

Bild und Urbild

Bei einer zweistelligen Relation ${\displaystyle R\subseteq A\times B}$ bezeichnet man als das Bild einer Menge oder Klasse ${\displaystyle X}$ die Menge bzw. Klasse

${\displaystyle R^{\to }(X)\equiv R\langle X\rangle$ :=\{y\mid \exists x\in X\colon \;(x,y)\in R\}} .

Das Urbild einer Menge oder Klasse ${\displaystyle Y}$ ist die Menge bzw. Klasse

${\displaystyle R^{\leftarrow }(Y)\equiv {\overset {\smallsmile }{R}}\langle Y\rangle \equiv {}^{\smallsmile }{R}\langle Y\rangle \equiv R^{\sim }\langle Y\rangle \equiv R^{-1}\langle Y\rangle =\{x\mid \exists y\in Y\colon \;(x,y)\in R\}}$.^[33][34][35]

Gelegentlich findet sich hierfür auch die Bezeichnung ${\displaystyle R{\grave {}}{\grave {}}Y}$ (sic!),^[30][36] oft auch mit eckigen Klammern als ${\displaystyle R[Y]}$ notiert. Bei Korrespondenzen ist für die Bildfaser einer Einermenge (Singleton) ${\displaystyle \{a\}}$ auch die Schreibweise ${\displaystyle \kappa _{R}(a)=R\langle \{a\}\rangle }$ im Gebrauch, wofür teilweise ebenfalls die Notation mit eckigen Klammern verwendet wird, d. h. ${\displaystyle R[a]}$;^[37] im Fall symmetrischer Relationen, d. h. (ggf. partieller) Äquivalenz- bzw. Verträglichkeitsrelationen ist die Notation ${\displaystyle [a]_{R}=R\langle \{a\}\rangle =R^{-1}\langle \{a\}\rangle }$ und spricht von Äquivalenz- bzw. Verträglichkeits- oder Toleranzklassen.

Einschränkung

Relationen lassen sich auf verschiedene Art und Weise auf Teilmengen der Trägermengen einschränken, Näheres siehe Einschränkung einer Relation.

Komplementäre Relation

Für zweistellige Relationen ${\displaystyle R\subseteq A\times B}$ bei festem Vor- und Nachbereich ${\displaystyle A,B}$ ist die komplementäre Relation gegeben durch^[38]

${\displaystyle {\overline {R}}\equiv {}^{-}R=(A\times B)\setminus R=\{(x,y)\in A\times B\mid (x,y)\not \in R\}}$,

analog für ${\displaystyle n}$-stellige Relationen ${\displaystyle R\subseteq A_{1}\times \dotsb \times A_{n}}$ bei festen Trägerbereichen ${\displaystyle A=(A_{1},\dotsc ,A_{n})}$. Auf den reellen Zahlen ${\displaystyle \mathbb {R} }$ ist beispielsweise ${\displaystyle \leq }$ die komplementäre Relation zu ${\displaystyle >}$.

Wird die komplexe Notation ${\displaystyle R=(G_{R},A,B)}$ zugrunde gelegt, so ist

${\displaystyle {\overline {R}}\equiv {}^{-}R=((A\times B)\setminus G_{R},A,B)}$,

wobei ${\displaystyle A,B}$ jetzt keine äußeren Zugaben mehr sind, sondern Bestandteile der Relation; analog für ${\displaystyle n}$-stellige Relationen in dieser Notation.

Wie für alle Mengen ist das Komplement auch für Relationen involutiv:

${\displaystyle {\overline {\overline {R}}}=R}$.

Homogene Relationen

Ist ${\displaystyle A=B}$, also ${\displaystyle R\subseteq A\times A}$, dann nennt man die Relation homogen. Manche Autoren definieren eine allgemeine Relation bereits als homogene Relation, denn eine allgemeine Relation ${\displaystyle R\subseteq A\times B}$ kann immer auch als Einschränkung einer homogenen betrachtet werden: ${\displaystyle R\subseteq (A\cup B)\times (A\cup B)}$.

Spezielle homogene Relationen und Operationen auf homogenen Relationen

Eine spezielle homogene Relation in einer Menge ${\displaystyle A}$ ist die Gleichheits- oder Identitätsrelation oder Diagonale

${\displaystyle \mathrm {I} _{A}:=\{(a,b)\in A\times A\mid a=b\}=\{(a,a)\mid a\in A\}.}$

Alternative Notationen für die Diagonale sind ${\displaystyle \Delta _{A}}$ oder ${\displaystyle \mathrm {D} _{A}}$; wenn ${\displaystyle A}$ bereits bekannt ist, wird sie einfach mit ${\displaystyle \mathrm {I} }$, ${\displaystyle \Delta }$ oder ${\displaystyle \mathrm {D} }$ bezeichnet.^[39]

Eine weitere spezielle homogene Relation ist die Allrelation oder Universalrelation

${\displaystyle \mathrm {U} _{A}=A\times A}$ (auch mit Nabla als ${\displaystyle \nabla _{A}}$ bezeichnet).

Wenn ${\displaystyle A}$ bereits bekannt ist, wird wie bei der Identitätsrelation auch hier der Index weggelassen.^[40]

Die Allrelation spielt eine Rolle in der Graphentheorie (siehe unten). Ein Anwendungsbeispiel ist folgender Satz:

Ist ${\displaystyle G=(E,K)}$ ein gerichteter Graph mit einer Menge ${\displaystyle E}$ von Ecken und einer (assoziierten) Relation ${\displaystyle K\subseteq E\times E}$ von Kanten, so ist ${\displaystyle G}$ genau dann (stark) zusammenhängend, wenn die reflexiv-transitive Hülle von ${\displaystyle K}$ die Universalrelation ist.

Die Bildung der Umkehrrelation (konversen Relation) einer homogenen zweistelligen Relation liefert wieder eine homogene zweistellige Relation (Abgeschlossenheit), zweimalige Ausführung ergibt wieder die Ausgangsrelation (Involutivität). Die Verknüpfung einer beliebigen (auch nicht-homogenen) Relation mit der dazu konversen Relation ist symmetrisch und reflexiv, also eine Äquivalenzrelation, aber im Allgemeinen nicht gleich der Identitätsrelation.^[29]

Im Fall einer homogenen Relation ${\displaystyle R\subseteq A\times A}$ ist die Verkettung ${\displaystyle R\circ R}$ ebenfalls eine homogene Relation, sodass die homogenen Relationen in ${\displaystyle A}$ ein Monoid mit der multiplikativen Verknüpfung ${\displaystyle \circ }$ und dem neutralen Element ${\displaystyle \mathrm {I} _{A}}$ bilden. Somit kann ${\displaystyle R^{2}:=R\circ R}$ und können allgemeiner Potenzen ${\displaystyle R^{n}:=R\circ R^{n-1}}$ für ${\displaystyle n\in \mathbb {N} }$ definiert werden, wobei ${\displaystyle R^{0}:=\mathrm {I} _{A}}$ ist.^[41] ${\displaystyle \mathrm {I} _{A}}$ wird daher auch Einsrelation auf der Menge ${\displaystyle A}$ genannt.

In Erweiterung der Notation ${\displaystyle R^{-1}}$ anstelle von ${\displaystyle {\overset {\smallsmile }{R}}}$ für die Umkehrrelation bezeichnet man deren Potenzen mit negativen Exponenten:^[42]

${\displaystyle R^{-n}:={\overset {\smallsmile }{R}}^{n}={\overset {\smallsmile }{R^{n}}}}$.

Damit sind beliebige ganze Zahlen ${\displaystyle n\in \mathbb {Z} }$ als Exponent zulässig.

Zudem besitzt jedes Monoid homogener Relationen mit der leeren Relation (Nullrelation)

${\displaystyle \mathrm {O} =\emptyset }$

noch ein absorbierendes Element.

Durch Vereinigung der verschiedenen Potenzen entstehen die Relationen^[43][42]

${\displaystyle R^{*}:=\textstyle \bigcup _{n\in {\mathbb {N} _{0}}}R^{n}}$ und ${\displaystyle R^{+}:=\textstyle \bigcup _{n\in {\mathbb {N} }}R^{n}}$. ^[44]

Algebraische Strukturen

Alles zusammengefasst, bilden die zweistelligen Relationen auf einer Menge ${\displaystyle A}$ eine Relationsalgebra

${\displaystyle {\mathfrak {Re}}(A)=(2^{U_{A}},\cap ,\cup ,{}^{-},\mathrm {O} ,U_{A},\circ ,\mathrm {I} _{A},{}^{\smallsmile })}$^[45]

Unter Verwendung der Notationen ${\displaystyle U_{A}=A^{2}=A\times A,\;\;2^{U_{A}}=2^{A^{2}}={\mathcal {P}}(A\times A)}$.^[46]

Zusammen mit den Beschränkungen bilden die homogenen Relationen eine (heterogene) Peirce-Algebra.^[47]

Homogene mehrstellige Relationen

Homogene mehrstellige Relationen sind (mit ihrem Graphen) Teilmengen von ${\displaystyle A^{n}}$. Für festes ${\displaystyle n}$ sind die Allrelation ${\displaystyle \mathrm {U} _{A}}$ (auch ${\displaystyle \nabla _{A}}$) und die Identitätsrelation (Diagonale) ${\displaystyle \mathrm {I} _{A}}$ (auch ${\displaystyle \mathrm {D} _{A},\Delta _{A}}$) gegeben durch

${\displaystyle \mathrm {U} _{A}=A^{n},\;\;\mathrm {I} _{A}=\{(a_{i})_{i\in \{1,\dotsc ,n\}}\in A^{n}\mid a_{1}=a_{2}=\dotsb =a_{n}\}}$.

Die als Verallgemeinerung der Konversenbildung beschriebene Anwendung von Permutationen auf ihre ${\displaystyle n}$-Tupel sind hier von besonderer Bedeutung, da man auf diese Weise immer innerhalb der Teilmengen von ${\displaystyle A^{n}}$ bleibt (Abgeschlossenheit). M. a. W. sind diese Operationen bijektive Abbildungen in ${\displaystyle {\mathcal {P}}(A^{n})=2^{A^{n}}}$. Auch weitere von zweistelligen Relationen bekannte Begriffe wie Reflexivität und Symmetrie etc. lassen sich in kanonischer (natürlicher) Weise auf beliebig mehrstellige Relationen ausdehnen.

Graphentheorie und Verallgemeinerungen

→ Hauptartikel: Graphentheorie

Die Graphentheorie beschreibt Mengen mit einer Relation darauf zusammen mit gewissen Verallgemeinerungen unter einem gemeinsamen Oberbegriff, dem Graphen.^[48] Die in der Graphentheorie betrachteten Fälle sind (wenn nicht anders angegeben) üblicherweise endlich (finit).

1. Eine relationale Struktur ${\displaystyle G}$ bestehend aus einer Menge ${\displaystyle M}$ zusammen mit einer Relation ${\displaystyle R}$ darauf wird als gerichteter (auch orientierter) Graph ${\displaystyle G=(M,R)}$ bezeichnet. ${\displaystyle M=V(G)}$ wird Knotenmenge des Graphen genannt, ihre Elemente heißen Knoten. ${\displaystyle E(G)=R}$ wird als Teilmenge von ${\displaystyle M\times M}$ als Kantenmenge bezeichnet, ihre Elemente (geordnete Paare aus ${\displaystyle M}$) heißen gerichtete (d. h. orientierte) Kanten.

2. Symmetrische Graphen ${\displaystyle G=(M,R)}$, d. h. Mengen ${\displaystyle M}$ mit einer symmetrischen Relation ${\displaystyle R}$, sind äquivalent einem ungerichteten Graphen ${\displaystyle G':=(M,\{\{a,b\}\mid a\;R\;b\})}$, dessen Kantenmenge ${\displaystyle E(G')}$ aus (ungerichteten) Kanten, nämlich den (ungeordnete) Mengen ${\displaystyle \{a,b\}}$ mit ${\displaystyle a\ R\ b}$ (hier äquivalent zu ${\displaystyle b\ R\ a}$) besteht.

3. Weitere Verallgemeinerungen betreffen sogenannte gerichtete Graphen mit zusammengefassten Mehrfachkanten, bei denen jede Kante eine natürliche Zahl als Multiplizität hat. Die Kanten solcher Graphen können durch eine Multimenge ${\displaystyle {\boldsymbol {M}}}$ dargestellt werden: eine Abbildung ${\displaystyle {\boldsymbol {M}}=(M,f)}$ mit einer Menge ${\displaystyle M=supp({\boldsymbol {M}})}$ und einer Abbildung ${\displaystyle f\colon \;M\to \mathbb {N} }$, die jedem Knoten ${\displaystyle v\in M}$ eine Farbe genannte positive Zahl ${\displaystyle f(v)}$ zuordnet. Ähnlich sind Graphen mit gefärbte Knoten und/oder Kanten.^[49]

4. Von gewichteten Knoten und/oder Kanten: Von Gewichten anstelle von Farben spricht man, wenn die Abbildung ${\displaystyle f}$ reellwertig ist. Bei ${\displaystyle f\colon \;M\to [0,1]}$ gewichteten Knoten entspricht dies einer Fuzzymenge ${\displaystyle {\boldsymbol {M}}=(M,f)}$, bei ${\displaystyle f\colon \;M\to R^{+}}$ ist ${\displaystyle {\boldsymbol {M}}=(M,f)}$ ein real valued multiset.^[50] Entsprechendes gilt für gewichtete Kanten. Für orientierte Graphen bedeutet dies insbesondere, dass die Kantenmenge (eine Relation, d. h. Menge geordneter Knotenpaare) in einer Erweiterung des Relationsbegriffs zu einer Multimenge oder Fuzzymenge wird.

Beispiele

• 
  Alle möglichen geordneten Paare ${\displaystyle (u,v)}$ mit ${\displaystyle u\in A:=\{a,b,c\}}$ und ${\displaystyle v\in B:=\{x,y,z\}}$ sowie eine zwischen ${\displaystyle A}$ und ${\displaystyle B}$ definierte Relation ${\displaystyle R.}$
• 
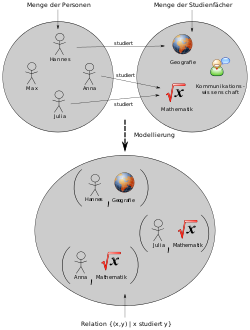
  Beispiel einer Relation „Eine Person x studiert das Fach y“.
• 
  Beispiel einer Relation „Person x liebt Person y“. Diese zweistellige Relation wird über eine Menge von geordneten Paaren modelliert.
• 
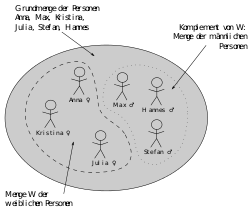
  Die einstellige Relation „Person x ist weiblich“ wird als Teilmenge der Grundmenge modelliert.
• 
  Die dreistellige Relation „Person x lernt das Fach y beim Lehrer z“ wird über eine Menge von 3-Tupeln realisiert.

Eigenschaften zweistelliger Relationen

Allgemeine Relationen

Die folgenden Relationen sind für Funktionen (dargestellt als spezielle Relationen) wichtig. Im Allgemeinen besteht hier die Relation ${\displaystyle R\subseteq A\times B}$ zwischen zwei verschiedenen Mengen ${\displaystyle A,B,}$ der Fall ${\displaystyle A=B}$ ist natürlich auch möglich.

Die Relation ${\displaystyle R}$ heißt	genau dann, wenn (Prädikatenlogik)	oder gleichwertig (Mengenschreibweise)	und das bedeutet:
linkstotal bzw. definal (Multifunktion)	${\displaystyle \forall a\in A\;\exists b\in {B}\colon \;(a,b)\in R}$	${\displaystyle \mathrm {I} _{A}\subseteq R^{-1}\circ R}$	Jedes Element aus ${\displaystyle A}$ hat mindestens einen Partner in ${\displaystyle B.}$
rechtstotal bzw. surjektiv	${\displaystyle \forall b\in B\;\exists a\in A\colon \;(a,b)\in R}$	${\displaystyle \mathrm {I} _{B}\subseteq R\circ R^{-1}}$	Jedes Element aus ${\displaystyle B}$ hat mindestens einen Partner in ${\displaystyle A.}$
linkseindeutig bzw. injektiv	${\displaystyle {\begin{aligned}&\forall b\in B\;\forall a,c\in A\colon \\&(a,b)\in R\,\land \,(c,b)\in R\;\Rightarrow \;a=c\end{aligned}}}$	${\displaystyle R^{-1}\circ R\subseteq \mathrm {I} _{A}}$	Jedes Element aus ${\displaystyle B}$ hat höchstens einen Partner in ${\displaystyle A.}$
(rechts-) eindeutig (partielle Funktion)	${\displaystyle {\begin{aligned}&\forall a\in A\;\forall b,d\in B\colon \\&(a,b)\in R\,\land \,(a,d)\in R\;\Rightarrow \;b=d\end{aligned}}}$	${\displaystyle R\circ R^{-1}\subseteq \mathrm {I} _{B}}$	Jedes Element aus ${\displaystyle A}$ hat höchstens einen Partner in ${\displaystyle B.}$

Die Relation ${\displaystyle R}$ heißt	genau dann, wenn (Prädikatenlogik)	oder gleichwertig (Mengenschreibweise)	und das bedeutet:
bitotal	${\displaystyle {\begin{aligned}&(\forall a\in A\;\exists b\in B\colon \;(a,b)\in R)\\\land \;&(\forall b\in B\;\exists a\in A\colon \;(a,b)\in R)\end{aligned}}}$	${\displaystyle {\begin{aligned}&\mathrm {I} _{A}\subseteq R^{-1}\circ R\\\land \;&\mathrm {I} _{B}\subseteq R\circ R^{-1}\end{aligned}}}$	Jedes Element aus ${\displaystyle A}$ hat mindestens einen Partner in ${\displaystyle B}$ und umgekehrt.
eineindeutig	${\displaystyle {\begin{aligned}&\forall b,d\in B\;\forall a,c\in A\colon \\&(a,b)\in R\,\land \,(c,b)\in R\;\Rightarrow \;a=c,\\&(a,b)\in R\,\land \,(a,d)\in R\;\Rightarrow \;b=d\end{aligned}}}$	${\displaystyle {\begin{aligned}&R^{-1}\circ R\subseteq \mathrm {I} _{A}\\\land \;&R\circ R^{-1}\subseteq \mathrm {I} _{B}\end{aligned}}}$	Jedes Element aus ${\displaystyle B}$ hat höchstens einen Partner in ${\displaystyle A}$ und umgekehrt.
bijektiv	${\displaystyle \forall b\in B\;\exists !a\in A\colon \;(a,b)\in R}$	${\displaystyle {\begin{aligned}&\mathrm {I} _{B}\subseteq R\circ R^{-1}\\\land \;&R^{-1}\circ R\subseteq \mathrm {I} _{A}\end{aligned}}}$	Jedes Element aus ${\displaystyle B}$ hat genau einen Partner in ${\displaystyle A.}$
Abbildung bzw. Funktion	${\displaystyle \forall a\in A\;\exists !b\in B\colon \;(a,b)\in R}$	${\displaystyle {\begin{aligned}&\mathrm {I} _{A}\subseteq R^{-1}\circ R\\\land \;&R\circ R^{-1}\subseteq \mathrm {I} _{B}\end{aligned}}}$	Jedes Element aus ${\displaystyle A}$ hat genau einen Partner in ${\displaystyle B.}$

Funktionen

Übersicht über Funktionseigenschaften bei Relationen

Eine Relation ist also genau dann eine (totale) Funktion, wenn sie linkstotal und rechtseindeutig ist. Das heißt, dass jedes Element in A genau einen Partner in B hat. Die Eigenschaften surjektiv, injektiv und bijektiv werden in der Regel für Funktionen gebraucht und spezifizieren bestimmte zusätzliche Eigenschaften. Z. B. ist eine Funktion (und auch eine beliebige Relation) ${\displaystyle R}$ genau dann bijektiv, wenn sie surjektiv und injektiv ist, also wenn ihre Umkehrrelation ${\displaystyle R^{-1}}$ eine Funktion ist.

Die Relation ${\displaystyle R}$ heißt	genau dann, wenn sie eine	ist oder gleichwertig (Mengenschreibweise)	und das bedeutet:
Surjektion	surjektive Funktion	${\displaystyle {\begin{aligned}&\mathrm {I} _{A}\subseteq R^{-1}\circ R\\\land \;&R\circ R^{-1}=\mathrm {I} _{B}\end{aligned}}}$	Jedes Element aus ${\displaystyle A}$ hat genau einen Partner in ${\displaystyle B}$ und jedes Element aus ${\displaystyle B}$ hat mindestens einen Partner in ${\displaystyle A.}$
Injektion	injektive Funktion	${\displaystyle {\begin{aligned}&\mathrm {I} _{A}=R^{-1}\circ R\\\land \;&R\circ R^{-1}\subseteq \mathrm {I} _{B}\end{aligned}}}$	Jedes Element aus ${\displaystyle A}$ hat genau einen Partner in ${\displaystyle B}$ und jedes Element aus ${\displaystyle B}$ hat höchstens einen Partner in ${\displaystyle A.}$
Bijektion	bijektive Funktion	${\displaystyle {\begin{aligned}&\mathrm {I} _{A}=R^{-1}\circ R\\\land \;&R\circ R^{-1}=\mathrm {I} _{B}\end{aligned}}}$	Jedes Element aus ${\displaystyle A}$ hat genau einen Partner in ${\displaystyle B}$ und umgekehrt.

Umkehrfunktion

Eine Abbildung bzw. Funktion nennt man auch

• umkehrbar eindeutig oder umkehrbar, falls sie bijektiv ist.

Eine Funktion ist als Relation immer umkehrbar, als Funktion ist sie dagegen genau dann umkehrbar, wenn ihre Umkehrrelation auch wieder eine Funktion ist, also wenn es eine Umkehrfunktion von ihr gibt.

Homogene Relationen

Die in den folgenden Tabellen gegebenen Beispiele beziehen sich bei Verwendung von Gleichheitszeichen „=“, Kleinerzeichen „<“ und Kleinergleich-Zeichen „≤“ auf die gewöhnliche Anordnung reeller Zahlen.

Die Relation ${\displaystyle R}$ heißt	genau dann, wenn (Prädikatenlogik)	oder gleichwertig (Mengenschreibweise)	und das bedeutet:
rechtskomparativ bzw. drittengleich[51]	${\displaystyle {\begin{aligned}&\forall a,b,c\in A\colon \\&(a,c)\in R\,\land \,(b,c)\in R\\&\Rightarrow \;(a,b)\in R\end{aligned}}}$	${\displaystyle R^{-1}\circ R\subseteq R}$	Stehen zwei Elemente jeweils zu einem gleichen dritten Element in Relation, dann stehen auch sie zueinander in Relation. Z. B. gilt mit ${\displaystyle a=c}$ und ${\displaystyle b=c}$ stets ${\displaystyle a=b.}$
linkskomparativ bzw. euklidisch[52][53]	${\displaystyle {\begin{aligned}&\forall a,b,c\in A\colon \\&(a,b)\in R\,\land \,(a,c)\in R\\&\Rightarrow \;(b,c)\in R\end{aligned}}}$	${\displaystyle R\circ R^{-1}\subseteq R}$	Steht ein erstes Element jeweils zu einem zweiten und zu einem dritten Element in Relation, so stehen auch diese zueinander in Relation. Z. B. gilt mit ${\displaystyle a=b}$ und ${\displaystyle a=c}$ stets ebenso ${\displaystyle b=c.}$
transitiv	${\displaystyle {\begin{aligned}&\forall a,b,c\in A\colon \\&(a,b)\in R\,\land \,(b,c)\in R\\&\Rightarrow \;(a,c)\in R\end{aligned}}}$	${\displaystyle R\circ R\subseteq R}$	Steht ein erstes Element zu einem zweiten Element und dieses wiederum zu einem dritten Element in Relation, so steht auch das erste Element zum dritten Element in Relation. Z. B. folgt aus ${\displaystyle a<b}$ und ${\displaystyle b<c}$ stets ${\displaystyle a<c.}$
intransitiv	${\displaystyle {\begin{aligned}&\forall a,b,c\in A\colon \\&(a,b)\in R\,\land \,(b,c)\in R\\&\Rightarrow \;(a,c)\notin R\\\end{aligned}}}$	${\displaystyle (R\circ R)\cap R=\emptyset }$	Stehen zwei Elemente in Relation und zudem das zweite Element zu einem dritten Element in Relation, dann steht das erste Element zum dritten Element nicht in Relation. Z. B. ist jede natürliche Zahl ${\displaystyle n}$ die (unmittelbare) Vorgängerin von ${\displaystyle n+1}$ und ${\displaystyle n+1}$ die (unmittelbare) Vorgängerin von ${\displaystyle n+2,}$ aber ${\displaystyle n}$ ist nicht (unmittelbare) Vorgängerin von ${\displaystyle n+2.}$

Nichttransitivität (d. h. die Relation ist nicht transitiv), Intransitivität und negative Transitivität sind jeweils voneinander verschieden.

Die Relation ${\displaystyle R}$ heißt	genau dann, wenn (Prädikatenlogik)	oder gleichwertig (Mengenschreibweise)	und das bedeutet:
reflexiv	${\displaystyle \forall a\in A\colon (a,a)\in R}$	${\displaystyle \mathrm {I} \subseteq R}$	Jedes Element steht in Relation zu sich selbst, z. B. ist stets ${\displaystyle a\leq a.}$
		${\displaystyle \mathrm {I} \cap R=\mathrm {I} }$
irreflexiv	${\displaystyle \forall a\in A\colon (a,a)\notin R}$	${\displaystyle \mathrm {I} \cap R=\emptyset }$	Kein Element steht in Relation zu sich selbst, z. B. gilt ${\displaystyle a<a}$ für kein ${\displaystyle a.}$

Die Relation ${\displaystyle R}$ heißt	genau dann, wenn (Prädikatenlogik)	oder gleichwertig (Mengenschreibweise)	und das bedeutet:
symmetrisch	${\displaystyle {\begin{aligned}&\forall a,b\in A\colon \\&(a,b)\in R\;\Rightarrow \;(b,a)\in R\end{aligned}}}$	${\displaystyle R^{-1}\subseteq R}$	Die Relation ist ungerichtet, z. B. folgt aus ${\displaystyle a=b}$ stets ${\displaystyle b=a}$ (und umgekehrt)
		${\displaystyle R^{-1}=R}$
antisymmetrisch bzw. identitiv	${\displaystyle {\begin{aligned}&\forall a,b\in A\colon \\&(a,b)\in R\,\land \,(b,a)\in R\\&\Rightarrow \;a=b\end{aligned}}}$	${\displaystyle R^{-1}\cap R\subseteq \mathrm {I} }$	Es gibt keine zwei verschiedenen Elemente, die in beiden Richtungen in Relation stehen, z. B. folgt aus ${\displaystyle a\leq b}$ und ${\displaystyle b\leq a}$ stets ${\displaystyle a=b.}$
asymmetrisch	${\displaystyle {\begin{aligned}&\forall a,b\in A\colon \\&(a,b)\in R\;\Rightarrow \;(b,a)\notin R\end{aligned}}}$	${\displaystyle R^{-1}\cap R=\emptyset }$	Es gibt keine zwei Elemente, die in beiden Richtungen in Relation stehen, z. B. folgt aus ${\displaystyle a<b}$ stets, dass ${\displaystyle b<a}$ nicht gilt.

Die Relation ${\displaystyle R}$ heißt	genau dann, wenn (Prädikatenlogik)	oder gleichwertig (Mengenschreibweise)	und das bedeutet:
total bzw. vollständig	${\displaystyle {\begin{aligned}&\forall a,b\in A\colon \\&(a,b)\in R\,\lor \,(b,a)\in R\end{aligned}}}$	${\displaystyle R^{-1}\cup R=A\times A}$	Je zwei Elemente stehen in Relation, z. B. wenn stets ${\displaystyle a\leq b}$ oder ${\displaystyle b\leq a}$ gilt.
konnex[54] bzw. verbunden	${\displaystyle {\begin{aligned}&\forall a,b\in A\colon \\&a\neq b\\&\Rightarrow \;(a,b)\in R\,\lor \,(b,a)\in R\end{aligned}}}$	${\displaystyle R^{-1}\cup R\cup \mathrm {I} =A\times A}$	Je zwei verschiedene Elemente stehen in Relation, z. B. wenn stets ${\displaystyle a<b}$ oder ${\displaystyle b<a}$ (für ${\displaystyle a\neq b}$ ) gilt.
trichotom	${\displaystyle {\begin{aligned}&\forall a,b\in A\colon \\&((a,b)\in R\Rightarrow (b,a)\notin R)\,\land \\&(a\neq b\\&\Rightarrow \;(a,b)\in R\,\lor \,(b,a)\in R)\end{aligned}}}$	${\displaystyle {\begin{aligned}R^{-1}\cup R\cup \mathrm {I} &=A\times A\\\land \;R^{-1}\cap R&=\emptyset \end{aligned}}}$	Je zwei verschiedene Elemente stehen stets auf genau eine Weise in Relation, z. B. wenn stets entweder ${\displaystyle a<b}$ oder ${\displaystyle b<a}$ gilt.

Zwischen den Eigenschaften gelten folgende Zusammenhänge:

Zusammenhang der Eigenschaften binärer Relationen

Zwischen den Eigenschaften einer Relation ${\displaystyle R}$ und denen ihres Komplements ${\displaystyle {\overline {R}}}$ bestehen folgende Zusammenhänge:

• ${\displaystyle R}$ ist reflexiv ${\displaystyle \iff }$ ${\displaystyle {\overline {R}}}$ ist irreflexiv (und umgekehrt).
• ${\displaystyle R}$ ist symmetrisch ${\displaystyle \iff }$ ${\displaystyle {\overline {R}}}$ ist symmetrisch.
• ${\displaystyle R}$ ist antisymmetrisch ${\displaystyle \iff }$ ${\displaystyle {\overline {R}}}$ ist konnex (und umgekehrt).
• ${\displaystyle R}$ ist total ${\displaystyle \iff }$ ${\displaystyle {\overline {R}}}$ ist asymmetrisch (und umgekehrt).^[55]

Klassen von Relationen

Zusammenhänge zwischen verschiedenen zweistelligen Relationen

Weitere wichtige Klassen von Relationen und ihre Eigenschaften:

• Quasiordnung oder Präordnung: transitiv und reflexiv
• Verträglichkeitsrelation oder Toleranzrelation: verträglich (reflexiv und symmetrisch)^[56] (englisch: im finiten Fall dependency relation, im transfiniten Fall tolerance relation).
• Äquivalenzrelation: transitiv, reflexiv und symmetrisch
• Halbordnung/Teilordnung, partielle Ordnung oder Ordnung: transitiv, reflexiv und antisymmetrisch.
• Vollordnung/Totalordnung oder lineare Ordnung: transitiv, reflexiv, antisymmetrisch und total
• Wohlordnung: eine lineare Ordnung, in der jede nichtleere Teilmenge von A ein kleinstes Element besitzt
• Striktordnung oder strenge Halbordnung/Teilordnung: transitiv, irreflexiv und antisymmetrisch (d. h. asymmetrisch)
• Strenge Vollordnung/Totalordnung oder lineare Striktordnung: transitiv, irreflexiv, antisymmetrisch und konnex

Relationszeichen

In der elementaren Mathematik gibt es drei grundlegende Vergleichsrelationen:

1. ${\displaystyle x<y}$ (Beispiel: ${\displaystyle 2<3,}$ „2 ist kleiner als 3“)
2. ${\displaystyle x=y}$ (Beispiel: ${\displaystyle 3=3,}$ „3 ist gleich 3“)
3. ${\displaystyle x>y}$ (Beispiel: ${\displaystyle 3>2,}$ „3 ist größer als 2“)

mit ${\displaystyle x,y\in \mathbb {R} }$.

Zwei reelle Zahlen stehen immer in genau einer dieser Relationen zueinander. Mit diesen Relationszeichen lassen sich auch weitere bilden. Es gilt:

• ${\displaystyle x\leq y}$, falls ${\displaystyle x<y}$ oder ${\displaystyle x=y}$ (Beispiel: ${\displaystyle 4\leq 5,}$ „4 ist nicht größer als 5“)
• ${\displaystyle x\geq y}$, falls ${\displaystyle x>y}$ oder ${\displaystyle x=y}$ (Beispiel: ${\displaystyle 5\geq 5,}$ „5 ist nicht kleiner als 5“)
• ${\displaystyle x\neq y}$, falls ${\displaystyle x<y}$ oder ${\displaystyle x>y}$ (Beispiel: ${\displaystyle 4\neq 5,}$ „4 ist nicht gleich 5“)

für alle ${\displaystyle x,y\in \mathbb {R} }$.

Für komplexe Zahlen existieren obige Ordnungsrelationen nicht.

Mathematiker verwenden das Zeichen ≤ auch für abstrakte Ordnungsrelationen (und ≥ für die zugehörige Umkehrrelation), während „<“ keine Ordnungsrelation im Sinne der mathematischen Definition ist.

Für Äquivalenzrelationen werden „symmetrische“ Symbole wie ≈, ~, ≡ bevorzugt.

Kategorientheorie

Für einen beliebigen Halbring ${\displaystyle (H,+,\cdot )}$ mit Nullelement ${\displaystyle 0}$ und Einselement ${\displaystyle 1}$ ist folgendes ${\displaystyle {\mathcal {C}}}$ eine Kategorie:

• ${\displaystyle \mathrm {Ob} ({\mathcal {C}})=\mathrm {Ob} (\mathbf {Set} )}$.
• Ein Morphismus ${\displaystyle f\in \mathrm {Hom} _{\mathcal {C}}(X,Y)}$ ist eine Funktion ${\displaystyle f\colon X\times Y\to H}$.
• Für Objekte ${\displaystyle X}$ gilt

  ${\displaystyle \mathrm {id} _{X}(x,x'):={\begin{cases}1&x=x'\\0&{\text{sonst}}\end{cases}}}$.

Das ist identisch mit dem Kronecker-Delta: ${\displaystyle \mathrm {id} _{X}(x,x')=\delta _{xx'}}$.

• Für Objekte ${\displaystyle X,Y,Z}$ und Morphismen ${\displaystyle f\in \mathrm {Hom} _{\mathcal {C}}(Y,Z),\ g\in \mathrm {Hom} _{\mathcal {C}}(X,Y)}$ gilt

  ${\displaystyle (f\circ g)(x,z):=\sum _{y\in Y}g(x,y)\cdot f(y,z)}$.

Die Morphismen sind also mengenindizierte Matrizen und ihre Komposition geschieht wie bei der Matrixmultiplikation, ${\displaystyle \mathrm {id} _{x}}$ entspricht der Einheitsmatrix ${\displaystyle E}$.

Im Sonderfall ${\displaystyle (H,+,\cdot )=(\{0,1\},\lor ,\land )}$ gilt ${\displaystyle {\mathcal {C}}=\mathbf {Rel} }$, d. h., ${\displaystyle {\mathcal {C}}}$ ist die Kategorie der Relationen.

Anwendung

Operationen auf ganzen Relationen werden in der relationalen Algebra untersucht. In der Informatik sind Relationen bei der Arbeit mit relationalen Datenbanken wichtig.

Siehe auch

• Kongruenzrelation
• Inzidenzrelation
• Prädikat (Logik)
• Fuzzy-Relation

Literatur

• Garrett Birkhoff: Lattice Theory. 3. Auflage. AMS, Providence, RI 1973, ISBN 0-8218-1025-1.
• Stefan Brass: Mathematische Logik mit Datenbank-Anwendungen. Martin-Luther-Universität Halle-Wittenberg, Institut für Informatik, Halle 2005, S. 176 (informatik.uni-halle.de [PDF]).
• Marcel Erné: Einführung in die Ordnungstheorie. Bibliographisches Institut, Mannheim 1982, ISBN 3-411-01638-8.
• Helmuth Gericke: Theorie der Verbände. Bibliographisches Institut, Mannheim 1963.
• Dieter Klaua: Mengenlehre. De Gruyter, Berlin / New York 1979, ISBN 3-11-007726-4 (Der Autor benutzt die Bezeichnung Korrespondenz im mengentheoretischen Sinn synonym zu Relation, verwendet dann aber das Zeichen ${\displaystyle F}$ anstelle von ${\displaystyle R}$. Im Artikel hier wird jedoch durchgängig ${\displaystyle R}$ bzw. ${\displaystyle G_{R}}$ (Graph von ${\displaystyle R}$) geschrieben).
• H. König: Entwurf und Strukturtheorie von Steuerungen für Fertigungseinrichtungen (= ISW Forschung und Praxis. Band 13). Springer, Berlin/Heidelberg 1976, ISBN 3-540-07669-7, S. 15–17, doi:10.1007/978-3-642-81027-5_1.
• Ingmar Lehmann, Wolfgang Schulz: Mengen – Relationen – Funktionen. Eine anschauliche Einführung. 3., überarbeitete und erweiterte Auflage. Vieweg+Teubner, Wiesbaden 2007, ISBN 978-3-8351-0162-3.
• Heike Mildenberger: Axiomatische Mengenlehre. Universität Freiburg, 9. November 2015, S. 58 (mathematik.uni-freiburg.de [PDF]).
• Willard van Orman Quine: Mengenlehre und ihre Logik (= Logik und Grundlagen der Mathematik. Band 10). Vieweg+Teubner, Wiesbaden 1973, ISBN 3-528-08294-1, S. 264 (amerikanisches Englisch: Set Theory And Its Logic. Cambridge, MA 1963. Ullstein 1978 als Taschenbuch).
• Gerard O’Regan: Guide to Discrete Mathematics. Sets, Relations and Functions (= Texts in Computer Science (TCS)). Springer, Schweiz 2016, S. 25–51, doi:10.1007/978-3-319-44561-8_2 (springer.com [PDF; 1000 kB]).
• Fritz Reinhardt, Heinrich Soeder: dtv-Atlas Mathematik. 11. Auflage. Band 1: Grundlagen, Algebra und Geometrie. Deutscher Taschenbuchverlag, München 1998, ISBN 3-423-03007-0, S. 30–33, 42–45.
• Gunther Schmidt, Thomas Ströhlein: Relationen und Graphen. Springer, Berlin u. a. 1989, ISBN 3-540-50304-8.
• Robert Wall: Einführung in die Logik und Mathematik für Linguisten. Band 1: Logik und Mengenlehre. Scriptor, Kronberg/Ts. 1974, ISBN 3-589-00023-6.
• Siegfried Wendt: Nichtphysikalische Grundlagen der Informationstechnik – Interpretierte Formalismen. 2. Auflage. Springer, Berlin/Heidelberg 2013, ISBN 978-3-540-54452-4, doi:10.1007/978-3-642-87627-1 (books.google.de).

Weblinks

Wikibooks: Mathe für Nicht-Freaks: Relation – Lern- und Lehrmaterialien

Wikibooks: Mathe für Nicht-Freaks: Binäre Relation – Lern- und Lehrmaterialien

• Literatur über Relation im Katalog der Deutschen Nationalbibliothek
• Video: Idee der zweistelligen Relationen. Pädagogische Hochschule Heidelberg (PHHD) 2012, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/19788.

Einzelnachweise und Anmerkungen

1. G. Smolka: Programmierung: Kapitel 2 – Mengenlehre, bei: Universität des Saarlandes, 20. Mai 2003, § 2.5. Binäre Relationen, S. 15.
2. V A. Zorich & J. Schüle: Analysis 1. Springer-Verlag, 2006, ISBN 978-3-540-33278-7, S. 21 (Google Books).
3. Dieter Klaua: Mengenlehre. De Gruyter, Berlin 2016, ISBN 978-3-11-084381-1, S. 68 (Google Books).
4. Jaroslav Nešetril: Diskrete Mathematik. Springer-Verlag, 2013, ISBN 978-3-662-06756-7, S. 36 (Google Books).
5. Walter Gellert, Herbert Kästner, Siegfried Neuber (Hrsg.): Lexikon der Mathematik. Bibliographisches Institut Leipzig, 1979, S. 484.
6. Albert Monjallon: Einführung in die moderne Mathematik. Ausgabe 2. Springer-Verlag, 2013, ISBN 978-3-663-16043-4, S. 74. doi:10.1007/978-3-663-16043-4, (books.google.de)
7. Wilhelm Dangelmaier: Produktionstheorie 1: Methodische Grundlagen. Springer-Verlag, 2017, ISBN 978-3-662-54922-3, S. 478. doi:10.1007/978-3-662-54923-0 (books.google.de)
8. Dieter Klaua: Mengenlehre. Seite 62, Definition 5 (1. Teil).
9. H. König: Entwurf und Strukturtheorie von Steuerungen für Fertigungseinrichtungen. Seite 19.
10. Weitere Bezeichnungsweisen: ${\displaystyle V_{R},V(R)}$, in der englischsprachigen Literatur: ${\displaystyle \operatorname {dom} R}$, siehe:
    Gerard O’Regan: Sets, Relations and Functions. S. 36.
11. Dieter Klaua: Mengenlehre. Seite 62, Definition 5, (2. Teil).
12. Weitere Bezeichnungsweisen: ${\displaystyle N_{R},N(R)}$, in der englischsprachigen Literatur: ${\displaystyle \operatorname {rng} R}$, siehe:
    Gerard O’Regan: Sets, Relations and Functions. S. 36.
13. Dieter Klaua: Mengenlehre. Seite 62, Definition 5, (3. Teil).
14. In der Theorie algebraischer Strukturen benutzt man – besonders im Hinblick auf die Kategorientheorie die Begriffe domain und codomain meist im Sinn von Quell- und Zielmenge, während in einführenden Schriften zur Mengenlehre diese meist als Urbild- und Bildmenge definiert werden,
15. auch mengenähnlich, mengenartig, auf engl.: left-narrow bzw. set-like genannt, siehe Wikibooks: Mathematik-Glossar: Mathematische Attribute: vorgängerklein
16. Heike Mildenberger 2015, S. 59f.
17. Martin Ziegler: Vorlesung über Mengenlehre, Universität Freiburg, 1992–2014, S. 12.
18. Azriel Levy: Basic Set Theory (= Dover Books on Mathematics. Band 13). Courier Corporation, Newburyport 2012, ISBN 978-0-486-15073-4, S. 22, (online)
19. Falls Urelemente zugelassen sind: für Urelemente ${\displaystyle b}$ ist ${\displaystyle \{a\in A\mid a\in b\}=\emptyset }$, ebenfalls eine Menge.
20. Siehe auch: Axiomatic Set Theory, Getting a model of (ZF – Fnd) ∪ { ¬Fnd} from a model of ZF, Ben Gurion University (BGU) of the Negev, The Department of Mathematics, 2003.
21. Im allgemeinen Fall mit der Trägermengensequenz ${\displaystyle A=(A_{i})_{i\in \{1,\dots n\}}}$ ist die Allrelation ${\displaystyle \mathrm {U} _{A}=\textstyle \prod A}$, im homogenen Fall mit der n-fachen Trägermenge ${\displaystyle A}$ ist ${\displaystyle U_{A}=A^{n}}$.
22. Stefan Brass (2005), S. 19.
23. Die charakteristische Funktion als Wahrheitsfunktion entspricht daher einem logischen Prädikat, und in der Modelltheorie nennt man die Relationssymbole deswegen auch Prädikatsymbole, siehe Stefan Brass (2005) S. 16.
24. englisch: forward relational composition
25. Mathematics Stack Exchange: Forward and backward composition in relational algebra Diskussion der Verkettungsrichtungen im Zusammenhang mit der Verkettung von Funktionen als spezielle Relationen. Für geordnete Paare wird teilweise die Maplet-Notation verwendet: ${\displaystyle x\mapsto y\equiv (x,y)}$
26. Glossary of Z notation §Relations, University of Washington
27. Gelegentlich findet sich auch der Strichpunkt in Konturdarstellung.
    ${\displaystyle R{\mbox{⨟}}S}$ wird in Wikipedia aber hardware- und einstellungsabhängig nicht immer korrekt dargestellt.
28. englisch: backward relational composition
29. H. König: Entwurf und Strukturtheorie von Steuerungen für Fertigungseinrichtungen. Seite 21.
30. W. v. O. Quine: Mengenlehre und ihre Logik. Seite 47.
31. Relationsalgebra. In: Mathepedia.de.
32. Als Bijektion auch mit ${\displaystyle \pi \colon \{1,2,\dotsc ,n\}\operatorname {\twoheadrightarrow \!\!\!\!\!\!\!\!\!\!\;\;\rightarrowtail } \{1,2,\dotsc ,n\}}$ notiert.
33. Zur Notation ${\displaystyle R^{\to },R^{\leftarrow }}$ siehe Gary Hardegree: Set Theory, Chapter 2: Relations, University of Massachusetts, Amherst, Department of Philosophy, Herbst 2015, S. 11: D16 und D17. Im Gegensatz zu den anderen Notationen referenzieren diese Symbole Abbildungen (Funktionen) zwischen den Potenzmengen ${\displaystyle {\mathcal {P}}(A),{\mathcal {P}}(B)}$.
34. Sinngemäß: D. Klaua: Mengenlehre. S. 63, Definition 6 (a).
35. Bei Ordnungsrelationen und ähnlichen sprechen manche Autoren auch von Vorgängermenge oder -klasse, siehe Heike Mildenberger 2015, S. 6, Definition 1.12.
36. W. v. O. Quine: Mengenlehre und ihre Logik. Seite 17. Achtung: Der Ausdruck ist als Bild betitelt, definiert aber klar das Urbild (eine Menge von linksseitigen Koordinaten = Argumenten ${\displaystyle x}$). Man beachte, dass diese Notation hier im Vergleich zu Funktionen konträr verwendet wird, bei Funktionen steht diese für das Bild (eine Menge von rechtsseitigen Koordinaten = Funktionswerten ${\displaystyle y}$) einer Menge unter einer Funktion ${\displaystyle f}$. Dabei sind Funktionen spezielle Relationen. Siehe Bild (Mathematik) §Alternative Notationen.
37. Johannes Köbler: Einführung in die Theoretische Informatik: Relationen. Humboldt-Universität Berlin, Institut für Informatik WS2013/14, S. 68.
38. W. v. O. Quine: Mengenlehre und ihre Logik. Seite 17.
39. Der obigen ausführlichen Relationsdefinition folgend wird man die Diagonale als den Graphen der Identität verstehen: ${\displaystyle \mathrm {I} _{A}=(\Delta _{A},A,A)}$ (Relation) mit ${\displaystyle \Delta _{A}=\{(a,a)\mid a\in A\}}$ (Graph).
40. Der obigen ausführlichen Relationsdefinition folgend wird man in Analogie zur Diagonalen das Nabla als den Graphen der Allrelation verstehen: ${\displaystyle \mathrm {U} _{A}=(\nabla _{A},A,A)}$ (Relation) mit ${\displaystyle \nabla _{A}=A\times A}$ (Graph)
41. Das kann zu Verwechslungen mit dem kartesischen Produkt ${\displaystyle R^{n}=R_{1}\times \dotsb \times R_{n}}$ mit ${\displaystyle R=R_{1}=\dotsb =R_{n}}$ führen. Die Bedeutung ergibt sich jeweils aus dem Sinnzusammenhang.
42. Gerard O’Regan: Sets, Relations and Functions. S. 39.
43. Siehe dazu auch: Kleenesche Hülle.
44. Zu den Transitivitätseigenschaften dieser Vereinigungen siehe Proving that ${\displaystyle \bigcup _{n=1}^{\infty }R^{n}}$ is a transitive relation on A, auf: StackExchange: Mathematics 2018.
45. Robin Hirsch, Ian Hodkinson: Relation algebras. S. 7, auf: Third Indian Conference on Logic and its Applications (ICLA). 7.–11. Januar 2009, Chennai, India.
46. Von den Verknüpfungen ${\displaystyle {}^{-},{}^{\smallsmile }}$ (einstellig) sowie ${\displaystyle \cap ,\cup ,\circ }$ (zweistellig) sind – genau genommen – die Einschränkungen auf ${\displaystyle A}$ bzw. ${\displaystyle A^{2}}$ gemeint.
47. C. Brink, K. Britz, R. A. Schmidt: Peirce Algebras. (1994), S. 163f. In: M. Nivat, C. Rattray, T. Rus, G. Scollo (Hrsg.): Algebraic Methodology and Software Technology (AMAST’93). Workshops in Computing. Springer, London.
48. Der Begriff Graph im graphentheoretischen Sinn ist zu unterscheiden vom Begriff Graph einer Relation entsprechend der eingangs erwähnten ausführlichen Definition von Relationen (wie auch Abbildungen), welche in der Graphentheorie nicht verwendet wird.
49. Der Begriff Farbe rührt daher, dass man die entsprechend der Multimengentheorie als Multiplizität verstandene Zahl ${\displaystyle f(v)}$ in der bildlichen Darstellung als nummerncodierte Farbe der Kante ${\displaystyle v}$ wiedergibt, analog bei gefärbten Knoten ${\displaystyle e}$.
    Ein Beispiel für Farbnummern wären etwa die RAL-Farben.
50. W.D. Blizard: Real-valued Multisets and Fuzzy Sets. In: Fuzzy Sets and Systems. Vol. 33, 1989, S. 77–97. doi:10.1016/0165-0114(89)90218-2.
51. „Zwei Größen, die einer und derselben dritten gleich sind, sind untereinander gleich.“ Vgl.
    Henri Poincaré: Wissenschaft und Hypothese. Autor. dt. Ausg. m. erl. Anm. v. F. u. L. Lindemann. Teubner, Leipzig 1904, S. 36.
52. Wolfgang Rautenberg: Einführung in Die Mathematische Logik. Ein Lehrbuch. Vieweg + Teubner, Wiesbaden 2008, ISBN 978-3-8348-0578-2, S. 42.
53. Das 1. Axiom in Euklids Elementen kann dagegen auch als gleichbedeutend mit drittengleich angesehen werden.
54. Nicht selten wird konnex auch wie total definiert.
55. Man erkennt dies leicht anhand der obigen Tabellen (1. und 2. Spalte) unter Berücksichtigung von ${\displaystyle \neg (aRb)\iff a{\overline {R}}b}$, d. h. ${\displaystyle \neg (a,b)\in R\iff (a,b)\not \in R\iff (a,b)\in {\overline {R}}}$ und der prädikatenlogischen Regeln. Die Umkehrungen gelten wegen Involutivität ${\displaystyle {\overline {\overline {R}}}=R}$.
56. Wendt 2013, Seite 31

Normdaten (Sachbegriff): GND: 4177675-6 (lobid, OGND)