Loading AI tools
印度数学家(1887-1920) 来自维基百科,自由的百科全书
斯里尼瓦瑟·拉馬努金(英語: Srinivasa Ramanujan,坦米爾語:ஸ்ரீனிவாஸ ராமானுஜன் ஐயங்கார்,ISO 15919轉寫:Srīṉivāsa Rāmāṉujan Aiyaṅkār,又譯拉馬努詹、羅摩奴詹、拉曼努真,1887年12月22日—1920年4月26日),英國皇家學會院士,是印度史上最著名的數學家之一。擅長數論,其中多牽涉π、質數等數學常數的求和公式,以及整數拆分。慣以直覺(或稱為數感)導出公式,不喜歡做證明,而他的理論在之後往往被證明是對的。他所留下尚未被證明的公式,啟發了幾位菲爾茲獎獲得者的工作。1997年,《拉馬努金期刊》(Ramanujan Journal)創刊,用以發表有關「受到拉馬努金影響的數學領域」的研究論文。
斯里尼瓦瑟出生於英屬印度,屬於婆羅門種姓。1898年,斯里尼瓦瑟十歲的時候,進入英屬印度政府的一所小學就讀,在那裡他似乎第一次接觸到正規的數學。11歲時,他已經掌握了住在他家的房客的數學知識,他們是國立大學的學生。到13歲,從借來的書籍中掌握高等三角學的知識。他的天賦在14歲時開始顯露。他不僅在學生時期不斷獲得榮譽證書和獎學金,他還幫學校處理把1,200個學生(各有不同需要)分配給35個教師的後勤事務,他甚至在給定時間一半內完成測驗,還已經顯示出對無窮級數的熟練掌握;他那時的同校的人後來回憶說:「我們,包括老師,很少可以理解他,並對他『敬而遠之』」。但是,拉馬努金對於其他科目無法集中注意力,並在高中考試中不及格。在這個時期,他的生活相當窮困,經常到了挨餓的地步。

因為結了婚,他必須找到工作。憑藉著他的數學計算能力,他在清奈(舊稱馬德拉斯)到處找抄寫員的工作。最後他終於找到了一個工作,並在一個英國人的建議下和劍橋的研究人員取得聯繫。
作為清奈總會計師事務所的職員,拉馬努金渴望可以完全投入到數學中而不用做其他工作。他懇請有影響力的印度人給予支持,並在印度數學期刊上發表了一些論文,但並未得到支持。在這個時期,慕克吉(Ashutosh Mukherjee)爵士試圖支持他的事業。
在1913年拉馬努金發了一長串複雜的定理給三個劍橋的學術人士貝克(H. F. Baker)、霍布森(E. W. Hobson)、哈代(G. H. Hardy),只有三一學院的院士哈代注意到拉馬努金在定理中所展現的天賦。
讀完這位不知名印度業餘數學家的唐突來信後,哈代和他的同事利特爾伍德(J. E. Littlewood)評論道:「沒有一個定理可以放到世界上最高等的數學測試中。」即使戈弗雷·哈羅德·哈代是當時著名的數學家,而且是其中幾個領域中的專家,他仍說:「(拉馬努金所寫下的許多東西)完全打敗了我」、「我從沒見過任何如此美麗的東西。」
作為他的成果的一個例子,拉馬努金給出了漂亮的連分數:
其中是黃金分割。
經歷起初的一些懷疑過後,哈代回信給出了一些評論,要求其中一些發現的具體證明過程,並開始安排將拉馬努金帶到英國。作為正統的婆羅門,拉馬努金諮詢了他的旅行星象,因為出於宗教考慮,到外國去他可能失去他的種姓。拉馬努金的母親做了個夢,其中家族女神告訴她不要阻攔兒子的行程,所以他制定了行程,但他依舊盡力保持婆羅門的生活方式。
富有成果的合作開始了。哈代將之描述為:「我一生中最浪漫的事」。哈代評論拉馬努金的公式,有些他起先不能理解,他說:「只要看它們一眼就知道只有一流的數學家才能寫下它們。它們肯定是真的,因為如果不是的話,沒人能有足夠的想像力來發明他們。」哈代在艾狄胥對他的一次採訪中說他自己對數學最偉大的貢獻是發現了拉馬努金,並稱拉馬努金的天賦至少與數學巨人歐拉和雅可比(Carl Jacobi)相當。拉馬努金後來成為三一學院的院士,並得到了科學界最高級別的榮譽,英國皇家學會會員(FRS)。

健康問題困擾了他的後半生。由於過度投入研究工作,拉馬努金的健康在英國急劇惡化。壓力的加劇以及第一次世界大戰時蔬菜的稀缺導致病情變得更加嚴重。他被診斷為肺結核(Henderson, 1996年)以及嚴重維生素不足,但1994年由楊格(Dr. D.A.B Young)進行的對拉馬努金的醫療紀錄和症狀的分析結論為更可能他有肝變形蟲病,一種感染肝臟的寄生蟲。拉馬努金在清奈待了很長時間進一步證實這一點,那是這種疾病廣泛傳播的沿海城市。那在當時是很難診斷的疑症,但一旦診斷當時已可治癒(Berndt, 1998年)。他於1919年返回印度,之後不久便在貢伯戈訥姆去世,他送給這個世界最後的禮物是拉馬努金θ函數的發現。在他死後,他的妻子賈納姬(S. Janaki Ammal)搬到孟買,1950年回到清奈生活,直至1994年逝世。結婚時賈納姬才九歲,在當時的印度是相當常見的。
拉馬努金終生過著婆羅門的生活。關於他實際信仰的觀點有很多區別:他的第一個印度傳記作者把他描述為一個嚴格正統的婆羅門,而哈代(堅定的無神論者)相信他在涉及到形上學的方面基本上是一個不可知論者。
哈代報道了拉馬努金的一個斷言說所有宗教一樣正確。卡尼蓋爾(Robert Kanigel)的傳記則稱拉馬努金可能不會給哈代看到他宗教的一面;另一方面來講,卡尼蓋爾通常描寫哈代的負面形象。
拉馬努金將他的理解歸功於他的家族女神納瑪姬莉(Namagiri:被視為Lakshmi吉祥天女的化身),並表示在他的工作中向她尋求靈感。他經常說:「一個方程對我沒有意義,除非它傳達了神的旨意。」
在數學上,有洞察力和能推導出具體證明是截然不同的。拉馬努金天才地提出了大量的公式,供人深入研究,並開啟了新的研究方向。例如一些和圓周率相關的奇妙的無窮級數,像是:
這和如下事實相關:
他也提出許多恆等式,例如:
對所有θ都成立,此處Γ(z)代表伽瑪函數。
比較恆等式兩邊θ之不同冪的係數,就可以得出雙曲正割的許多恆等式。
哈代這樣評論拉馬努金:
| “ | 他知識不足的程度跟知識的深厚都讓人很吃驚。他是能夠發現模方程和定理的人……到達前所未聞的地步,他對連分數的掌握……超出了世界上任何一個數學家,他自己發現了ζ函數的泛函方程和解析數論中的很多著名問題中級數的主要項;但他卻沒有聽說過雙周期函數或者柯西定理,對複變函數只有非常模糊的概念…… | ” |
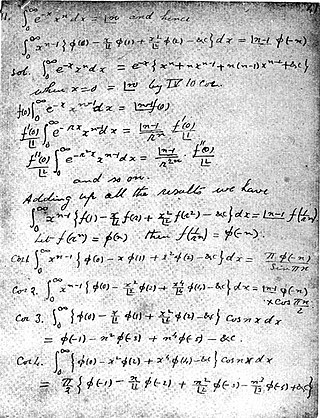
以下包括拉馬努金自己的發現,和與哈代的合作中發現和證明的定理
他也在下列領域做出重大突破和發現:
他的發現異常豐富;甚至很多在日後被發現,其內涵比原本乍看之下還要豐富許多。
雖然拉馬努金提出的很多命題都有資格被稱為拉馬努金(的)猜想,但其中一個特別有影響力,所以「拉馬努金猜想」通常指的是它。拉馬努金猜想斷定了拉馬努金τ函數的大小。這裡說的τ函數的生成函數是模判別式 Δ(q)(模形式理論中一種典型的尖形式(cusp form))。這個猜想在1973年終於被證明,可由皮埃爾·德利涅證明的魏依猜想推論而得,其化簡步驟相當複雜。
當他還在印度時,拉馬努金在三本活頁紙筆記上記錄了很多結果。結果被寫下來,但沒有推導過程。這可能是對拉馬努金不能證明自己的結果而只是直接想到最後結果的誤解的起源。Berndt在他對這些筆記和拉馬努金的工作的評論中,感到拉馬努金幾乎肯定能夠對他絕大部分的結果作出證明,只是選擇了不做證明。
這種工作風格可能有幾個原因。因為紙在那時很貴,拉馬努金在寫字石板上進行了他大部分的工作可能還有他的證明,然後只將結果轉移到紙上。在當時的印度,使用寫字板對於數學的學生來講很常見。他也可能受一本書的影響——他大部分的高等數學知識的來源卡爾(G. S. Carr))《純數學和應用數學概要》(Synopsis of Pure and Applied Mathematics),這是卡爾用來教授數學的。它總結了幾千個結果,不帶證明的給出了它們。最後,可能拉馬努金認為他的工作只是給他自己的個人興趣用的;所以只記錄了結果。(Berndt, 1998)
第一本筆記有351頁,大約16個有某種組織的章和一些無組織的材料。第二本筆記有256頁,散布在21章和100個無組織頁面中。第三本有33個未組織的頁面。他筆記本中的結果激發了大量論文,由後世企圖證明他的發現的數學家所寫。哈代自己也寫了挖掘拉馬努金工作中的材料的論文,就像沃森(G. N. Watson)、威爾遜(B. M. Wilson)和伯恩特(Bruce Berndt)所作的一樣。(Berndt, 1998)

拉馬努金是印度在過去一千年中所出非常偉大的數學家,他的直覺跳躍甚至令今天的數學家感到困惑與驚奇。在死後80多年,他的論文中所埋藏的秘密依然正在被挖掘。他的定理被應用到他活著的時候很難想像到的領域。[1]美國作家羅伯特·卡尼蓋爾所著傳記《知無涯者:拉馬努金傳》後被中國數學家,武漢大學前校長齊民友等翻譯成中文。
拉馬努金病重,哈代前往探望。哈代說:「我搭計程車來,車牌號碼是,這數字真沒趣,希望不是不祥之兆。」拉馬努金答道:「不,這個數有趣得很。在所有可以用兩個立方數之和來表達而且有兩種表達方式的數之中,是最小的。」(即,後來這類數稱為的士數。)哈代引述利特爾伍德的話說:「每個正整數都是拉馬努金的朋友。」[2]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.