常態分布

常態分布（normal distribution，中國大陸作正態分布），物理學中通稱高斯分布（Gaussian distribution）^[1]，是一個非常常見的連續機率分布。常態分布在統計學上十分重要，經常用在自然和社會科學來代表一個不明的隨機變數。^[2][3]

常態分布

機率密度函數 紅線代表標準常態分布
累積分布函數 顏色與機率密度函數相同
記號	${\displaystyle N(\mu ,\sigma ^{2})}$
母數	${\displaystyle \mu }$數學期望值（實數） ${\displaystyle \sigma ^{2}>0}$變異數（實數）
值域	${\displaystyle x\in (-\infty ;+\infty )\!}$
機率密度函數	${\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}\;\exp \left(-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right)\!}$
累積分布函數	${\displaystyle {\frac {1}{2}}\left(1+\operatorname {erf} {\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\!}$
期望值	${\displaystyle \mu }$
中位數	${\displaystyle \mu }$
眾數	${\displaystyle \mu }$
變異數	${\displaystyle \sigma ^{2}}$
偏度	0
峰度	0
熵	${\displaystyle \ln \left(\sigma {\sqrt {2\,\pi \,e}}\right)\!}$
動差母函數	${\displaystyle M_{X}(t)=\exp \left(\mu \,t+\sigma ^{2}{\frac {t^{2}}{2}}\right)}$
特徵函數	${\displaystyle \phi _{X}(t)=\exp \left(\mu \,i\,t-{\frac {\sigma ^{2}t^{2}}{2}}\right)}$

「normal distribution」的各地常用譯名
中國大陸	正態分布
臺灣	常態分布
港澳	常態分佈、正態分佈
日本	正規分布
韓國	正規分布

若隨機變數${\displaystyle X}$服從一個平均數為${\displaystyle \mu }$、標準差為${\displaystyle \sigma }$的常態分布，則記為：

${\displaystyle X\sim N(\mu ,\sigma ^{2}),}$^[4]

則其機率密度函數為 ${\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\;e^{-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}}\!}$^[4][5]

常態分布的數學期望值值或期望值${\displaystyle \mu }$,可解釋為位置母數，決定了分布的位置；其變異數${\displaystyle \sigma ^{2}}$的平方根或標準差${\displaystyle \sigma }$可解釋尺度母數，決定了分布的幅度。^[5]

中央極限定理指出，在特定條件下，一個具有有限均值和變異數的隨機變數的多個樣本(觀察值)的平均值本身就是一個隨機變數，其分布隨著樣本數量的增加而收斂於常態分布。因此，許多與獨立過程總和有關的物理量，例如測量誤差，通常可被近似為常態分布。

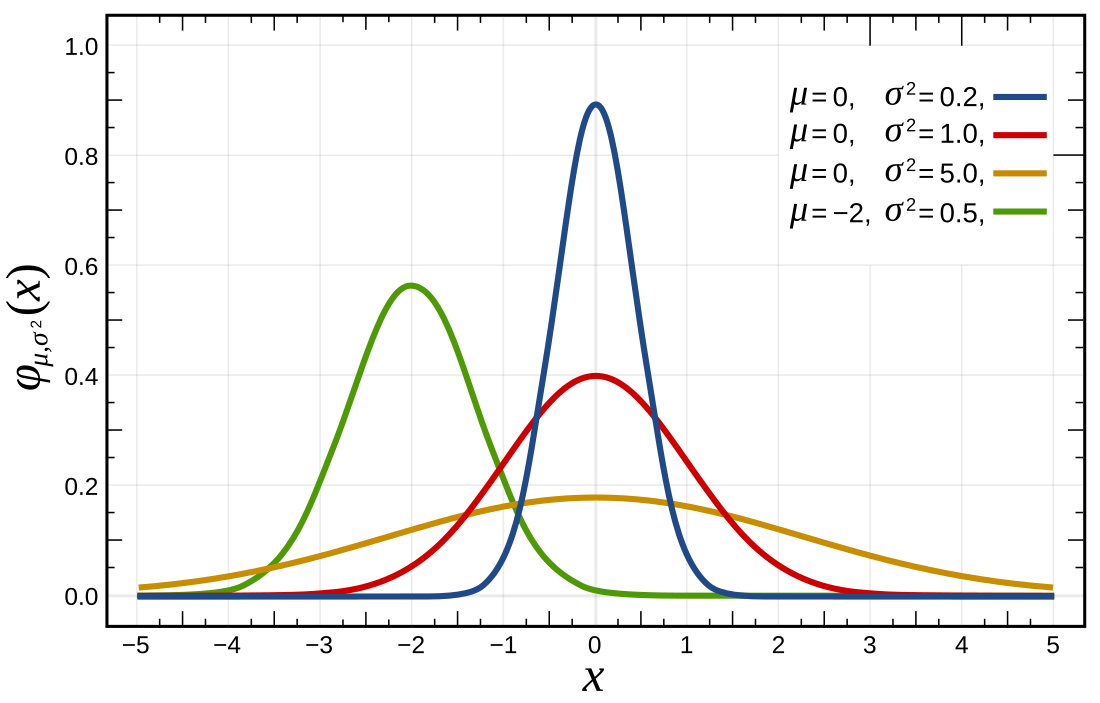
常態分布的機率密度函數曲線呈鐘形，因此人們又經常稱之為鐘形曲線（類似於寺廟裡的大鐘，因此得名）。我們通常所說的標準常態分布是位置母數${\displaystyle \mu =0}$，尺度母數${\displaystyle \sigma ^{2}=1}$的常態分布^[5]（見右圖中紅色曲線）。

概要

常態分布是自然科學與行為科學中的定量現象的一個方便模型。各種各樣的心理學測試分數和物理現象比如光子計數都被發現近似地服從常態分布。儘管這些現象的根本原因經常是未知的，理論上可以證明如果把許多小作用加起來看做一個變量，那麼這個變量服從常態分布（在R.N.Bracewell的Fourier transform and its application中可以找到一種簡單的證明）。常態分布出現在許多區域統計：例如，採樣分布均值是近似地常態的，即使被採樣的樣本的原始群體分布並不服從常態分布。另外，常態分布資訊熵在所有的已知均值及變異數的分布中最大，這使得它作為一種均值以及變異數已知的分布的自然選擇。常態分布是在統計以及許多統計測試中最廣泛應用的一類分布。在機率論，常態分布是幾種連續以及離散分布的極限分布。

歷史

常態分布最早是棣美弗在1718年著作的書籍的（Doctrine of Change），及1734年發表的一篇關於二項分布文章中提出的，當二項隨機變數的位置母數n很大及形狀母數p為1/2時，則所推導出二項分布的近似分布函數就是常態分布。拉普拉斯在1812年發表的《分析機率論》（Theorie Analytique des Probabilites）中對棣莫佛的結論作了擴展到二項分布的位置母數為n及形狀母數為1>p>0時。現在這一結論通常被稱為棣莫佛－拉普拉斯定理。

拉普拉斯在誤差分析試驗中使用了常態分布。勒讓德於1805年引入最小平方法這一重要方法；而高斯則宣稱他早在1794年就使用了該方法，並通過假設誤差服從常態分布給出了嚴格的證明。

將常態分布稱作「鐘形曲線」的習慣可以追溯到Jouffret他在1872年首次提出這個術語（Bell curve）用來指代二元常態分布。常態分布這個名字還被查爾斯·皮爾士、法蘭西斯·高爾頓、威爾赫姆·萊克希斯在1875分別獨立地使用。這個術語是不幸的，因為它反映和鼓勵了一種謬誤，即很多機率分布都是常態的。（請參考下面的「實例」）

這個分布被稱為「常態」或者「高斯」正好是史蒂格勒名字由來法則的一個例子，這個法則說「沒有科學發現是以它最初的發現者命名的」。

常態分布的定義

有幾種不同的方法用來說明一個隨機變數。最直觀的方法是機率密度函數，這種方法能夠表示隨機變數每個取值有多大的可能性。累積分布函數是一種機率上更加清楚的方法，請看下邊的例子。還有一些其他的等價方法，例如cumulant、特徵函數、動差生成函數以及cumulant-生成函數。這些方法中有一些對於理論工作非常有用，但是不夠直觀。請參考關於機率分布的討論。

機率密度函數

四個不同母數集的機率密度函數（紅色線代表標準常態分布）

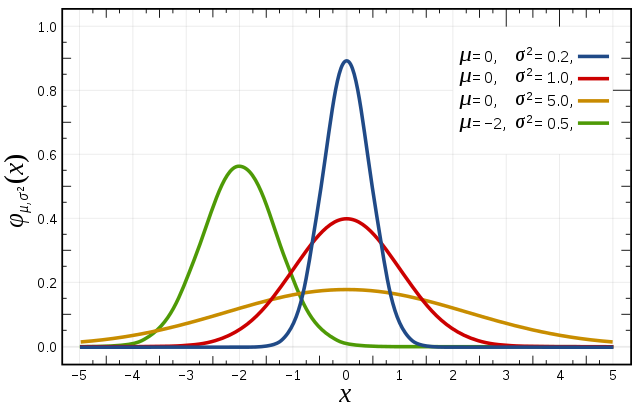
常態分布的機率密度函數均值為${\displaystyle \mu }$ 變異數為${\displaystyle \sigma ^{2}}$ (或標準差${\displaystyle \sigma }$)是高斯函數的一個實例：

${\displaystyle f(x;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\,\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)}$。

(請看指數函數以及${\displaystyle \pi }$.)

如果一個隨機變數${\displaystyle X}$服從這個分布，我們寫作 ${\displaystyle X}$ ~ ${\displaystyle N(\mu ,\sigma ^{2})}$. 如果${\displaystyle \mu =0}$並且${\displaystyle \sigma =1}$，這個分布被稱為標準常態分布，這個分布能夠簡化為

${\displaystyle f(x)={\frac {1}{\sqrt {2\pi }}}\,\exp \left(-{\frac {x^{2}}{2}}\right)}$。

右邊是給出了不同母數的常態分布的函數圖。

常態分布中一些值得注意的量：

• 密度函數關於平均值對稱
• 平均值與它的眾數（statistical mode）以及中位數（median）同一數值。
• 函數曲線下68.268949%的面積在平均數左右的一個標準差範圍內。
• 95.449974%的面積在平均數左右兩個標準差${\displaystyle 2\sigma }$的範圍內。
• 99.730020%的面積在平均數左右三個標準差${\displaystyle 3\sigma }$的範圍內。
• 99.993666%的面積在平均數左右四個標準差${\displaystyle 4\sigma }$的範圍內。
• 函數曲線的反曲點（inflection point）為離平均數一個標準差距離的位置。

累積分布函數

上圖所示的機率密度函數的累積分布函數

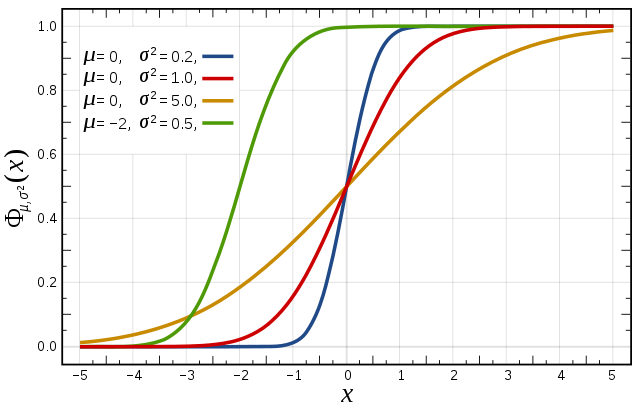
累積分布函數是指隨機變數${\displaystyle X}$小於或等於${\displaystyle x}$的機率，用機率密度函數表示為

${\displaystyle F(x;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{x}\exp \left(-{\frac {(t-\mu )^{2}}{2\sigma ^{2}}}\ \right)\,dt.}$

常態分布的累積分布函數能夠由一個叫做誤差函數的特殊函數表示：

${\displaystyle \Phi (z)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {z-\mu }{\sigma {\sqrt {2}}}}\right)\right].}$

標準常態分布的累積分布函數習慣上記為${\displaystyle \Phi }$，它僅僅是指${\displaystyle \mu =0}$，${\displaystyle \sigma =1}$時的值，

${\displaystyle \Phi (x)=F(x;0,1)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}\exp \left(-{\frac {t^{2}}{2}}\right)\,dt.}$

將一般常態分布用誤差函數表示的公式簡化，可得：

${\displaystyle \Phi (z)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {z}{\sqrt {2}}}\right)\right].}$

它的反函數被稱為反誤差函數，為：

${\displaystyle \Phi ^{-1}(p)={\sqrt {2}}\;\operatorname {erf} ^{-1}\left(2p-1\right).}$

該分位數函數有時也被稱為probit函數。probit函數已被證明沒有初等原函數。

常態分布的分布函數${\displaystyle \Phi (x)}$沒有解析表達式，它的值可以通過數值積分、泰勒級數或者漸進序列近似得到。

生成函數

動差母函數

動差生成函數，或稱動差母函數被定義為${\displaystyle \exp(tX)}$的期望值。

常態分布的動差產生函數如下：

${\displaystyle M_{X}(t)\,}$	${\displaystyle =\mathrm {E} \left(e^{tX}\right)}$
	${\displaystyle =\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)}e^{tx}\,dx}$
	${\displaystyle =e^{\left(\mu t+{\frac {\sigma ^{2}t^{2}}{2}}\right)}}$

可以通過在指數函數內配平方得到。

特徵函數

特徵函數被定義為${\displaystyle \exp(itX)}$的期望值，其中${\displaystyle i}$是虛數單位. 對於一個常態分布來講，特徵函數是：

${\displaystyle \phi _{X}(t;\mu ,\sigma )\!}$	${\displaystyle =\mathrm {E} \left[\exp(itX)\right]}$
	${\displaystyle =\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\exp(itx)\,dx}$
	${\displaystyle =\exp \left(i\mu t-{\frac {\sigma ^{2}t^{2}}{2}}\right).}$

把動差生成函數中的${\displaystyle t}$換成${\displaystyle it}$就能得到特徵函數。

性質

常態分布的一些性質：

1. 如果${\displaystyle X\sim N(\mu ,\sigma ^{2})\,}$且${\displaystyle a}$與${\displaystyle b}$是實數，那麼${\displaystyle aX+b\sim N(a\mu +b,(a\sigma )^{2})}$ (參見期望值和變異數).
2. 如果${\displaystyle X\sim N(\mu _{X},\sigma _{X}^{2})}$與${\displaystyle Y\sim N(\mu _{Y},\sigma _{Y}^{2})}$是統計獨立的常態隨機變數，那麼：
   • 它們的和也滿足常態分布${\displaystyle U=X+Y\sim N(\mu _{X}+\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$ (proof（英語：sum of normally distributed random variables）).
   • 它們的差也滿足常態分布${\displaystyle V=X-Y\sim N(\mu _{X}-\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$.
   • ${\displaystyle U}$與${\displaystyle V}$兩者是相互獨立的。（要求X與Y的變異數相等）
3. 如果${\displaystyle X\sim N(0,\sigma _{X}^{2})}$和${\displaystyle Y\sim N(0,\sigma _{Y}^{2})}$是獨立常態隨機變數，那麼：
   • 它們的積${\displaystyle XY}$服從機率密度函數為${\displaystyle p}$的分布

     ${\displaystyle p(z)={\frac {1}{\pi \,\sigma _{X}\,\sigma _{Y}}}\;K_{0}\left({\frac {|z|}{\sigma _{X}\,\sigma _{Y}}}\right),}$其中${\displaystyle K_{0}}$是修正貝塞爾函數（modified Bessel function）

   • 它們的比符合柯西分布，滿足${\displaystyle X/Y\sim \mathrm {Cauchy} (0,\sigma _{X}/\sigma _{Y})}$.
4. 如果${\displaystyle X_{1},\cdots ,X_{n}}$為獨立標準常態隨機變數，那麼${\displaystyle X_{1}^{2}+\cdots +X_{n}^{2}}$服從自由度為n的卡方分布。

標準化常態隨機變數

動差（moment）

一些常態分布的一階動差如下：

階數	原動差	主動差	累積量
0	1	0
1	${\displaystyle \mu }$	0	${\displaystyle \mu }$
2	${\displaystyle \mu ^{2}+\sigma ^{2}}$	${\displaystyle \sigma ^{2}}$	${\displaystyle \sigma ^{2}}$
3	${\displaystyle \mu ^{3}+3\mu \sigma ^{2}}$	0	0
4	${\displaystyle \mu ^{4}+6\mu ^{2}\sigma ^{2}+3\sigma ^{4}}$	${\displaystyle 3\sigma ^{4}}$	0

標準常態的所有二階以上的累積量為零。

生成常態隨機變數

中央極限定理

主條目：中央極限定理

常態分布的機率密度函數，母數為μ = 12，σ = 3，趨近於n = 48、p = 1/4的二項分布的機率質量函數。

常態分布有一個非常重要的性質：在特定條件下，大量統計獨立的隨機變數的平均值的分布趨於常態分布，這就是中央極限定理。中央極限定理的重要意義在於，根據這一定理的結論，其他機率分布可以用常態分布作為近似。

• 母數為${\displaystyle n}$和${\displaystyle p}$的二項分布，在${\displaystyle n}$相當大而且${\displaystyle p}$接近0.5時近似於常態分布（有的參考書建議僅在${\displaystyle np}$與${\displaystyle n(1-p)}$至少為5時才能使用這一近似）。

近似常態分布平均數為${\displaystyle \mu =np}$且變異數為${\displaystyle \sigma ^{2}=np(1-p)}$.

• 一卜瓦松分布帶有母數${\displaystyle \lambda }$當取樣樣本數很大時將近似常態分布${\displaystyle \lambda }$.

近似常態分布平均數為${\displaystyle \mu =\lambda }$且變異數為${\displaystyle \sigma ^{2}=\lambda }$.

這些近似值是否完全充分正確取決於使用者的使用需求

無限可分性

常態分布是無限可分的機率分布。

穩定性

常態分布是嚴格穩定的機率分布。

標準偏差

深藍色區域是距平均值小於一個標準差之內的數值範圍。在常態分布中，此範圍所佔比率為全部數值之68%，根據常態分布，兩個標準差之內的比率合起來為95%；三個標準差之內的比率合起來為99%。

在實際應用上，常考慮一組數據具有近似於常態分布的機率分布。若其假設正確，則約68.3%數值分布在距離平均值有1個標準差之內的範圍，約95.4%數值分布在距離平均值有2個標準差之內的範圍，以及約99.7%數值分布在距離平均值有3個標準差之內的範圍。稱為「68-95-99.7法則」或「經驗法則」。

數字比率 標準差值	機率	包含之外比例
	百分比	百分比	比例
6999318639000000000♠0.318639σ	25%	75%	3 / 4
6999674490000000000♠0.674490σ	7001500000000000000♠50%	7001500000000000000♠50%	1 / 7000200000000000000♠2
6999994458000000000♠0.994458σ	68%	32%	1 / 3.125
1σ	7001682689492000000♠68.2689492%	7001317310508000000♠31.7310508%	1 / 7000315148720000000♠3.1514872
7000128155200000000♠1.281552σ	80%	20%	1 / 5
7000164485400000000♠1.644854σ	90%	10%	1 / 10
7000195996400000000♠1.959964σ	95%	5%	1 / 20
2σ	7001954499736000000♠95.4499736%	7000455002640000000♠4.5500264%	1 / 7001219778950000000♠21.977895
7000257582900000000♠2.575829σ	99%	1%	1 / 100
3σ	7001997300204000000♠99.7300204%	6999269979600000000♠0.2699796%	1 / 370.398
7000329052700000000♠3.290527σ	99.9%	0.1%	1 / 7003100000000000000♠1000
7000389059200000000♠3.890592σ	99.99%	0.01%	1 / 7004100000000000000♠10000
4σ	7001999936660000000♠99.993666%	6997633400000000000♠0.006334%	1 / 7004157870000000000♠15787
7000441717300000000♠4.417173σ	99.999%	0.001%	1 / 7005100000000000000♠100000
7000450000000000000♠4.5σ	99.9993204653751%	0.0006795346249%	1 / 7005147159535800000♠147159.5358 3.4 / 7006100000000000000♠1000000 (每一邊)
7000489163800000000♠4.891638σ	7001999999000000000♠99.9999%	6996100000000000000♠0.0001%	1 / 7006100000000000000♠1000000
5σ	7001999999426697000♠99.9999426697%	6995573303000000000♠0.0000573303%	1 / 7006174427800000000♠1744278
7000532672399999999♠5.326724σ	7001999999900000000♠99.99999%	6995100000000000000♠0.00001%	1 / 7007100000000000000♠10000000
7000573072900000000♠5.730729σ	7001999999990000000♠99.999999%	6994100000000000000♠0.000001%	1 / 7008100000000000000♠100000000
7000600000000000000♠6σ	7001999999998027000♠99.9999998027%	6993197300000000000♠0.0000001973%	1 / 7008506797346000000♠506797346
7000610941000000000♠6.109410σ	7001999999999000000♠99.9999999%	6993100000000000000♠0.0000001%	1 / 7009100000000000000♠1000000000
7000646695100000000♠6.466951σ	7001999999999900000♠99.99999999%	6992100000000000000♠0.00000001%	1 / 7010100000000000000♠10000000000
7000680650200000000♠6.806502σ	7001999999999990000♠99.999999999%	6991100000000000000♠0.000000001%	1 / 7011100000000000000♠100000000000
7σ	99.9999999997440%	6990256000000000000♠0.000000000256%	1 / 7011390682215445000♠390682215445

相關分布

• ${\displaystyle R\sim \mathrm {Rayleigh} (\sigma )}$是瑞利分布，如果${\displaystyle R={\sqrt {X^{2}+Y^{2}}}}$，這裡${\displaystyle X\sim N(0,\sigma ^{2})}$和${\displaystyle Y\sim N(0,\sigma ^{2})}$是兩個獨立常態分布。
• ${\displaystyle Y\sim \chi _{\nu }^{2}}$是卡方分布具有${\displaystyle \nu }$自由度，如果${\displaystyle Y=\sum _{k=1}^{\nu }X_{k}^{2}}$這裡${\displaystyle X_{k}\sim N(0,1)}$其中${\displaystyle k=1,\dots ,\nu }$是獨立的。
• ${\displaystyle Y\sim \mathrm {Cauchy} (\mu =0,\theta =1)}$是柯西分布，如果${\displaystyle Y=X_{1}/X_{2}}$，其中${\displaystyle X_{1}\sim N(0,1)}$並且${\displaystyle X_{2}\sim N(0,1)}$是兩個獨立的常態分布。
• ${\displaystyle Y\sim {\mbox{Log-N}}(\mu ,\sigma ^{2})}$是對數常態分布如果${\displaystyle Y=e^{X}}$並且${\displaystyle X\sim N(\mu ,\sigma ^{2})}$.
• 與Lévy skew alpha-stable分布相關：如果${\displaystyle X\sim {\textrm {Levy-S}}\alpha {\textrm {S}}(2,\beta ,\sigma /{\sqrt {2}},\mu )}$因而${\displaystyle X\sim N(\mu ,\sigma ^{2})}$.

估計

母數的最大概似估計

概念一般化

多元常態分布的共變異數矩陣的估計的推導是比較難於理解的。它需要瞭解譜原理（spectral theorem）以及為什麼把一個標量看做一個1×1矩陣的跡（trace）而不僅僅是一個標量更合理的原因。請參考共變異數矩陣的估計（estimation of covariance matrices）。

母數的動差估計

常見實例

光子計數

計量誤差

飲料裝填量不足與超量的機率

某飲料公司裝瓶流程嚴謹，每罐飲料裝填量符合平均600毫升，標準差3毫升的常態分配法則。隨機選取一罐，求（1）容量超過605毫升的機率；（2）容量小於590毫升的機率。

容量超過605毫升的機率 = p ( X > 605)= p ( ((X-μ) /σ) > ( (605 – 600) / 3) )= p ( Z > 5/3) = p( Z > 1.67) = 1 - 0.9525 = 0.0475

容量小於590毫升的機率 = p (X < 590) = p ( ((X-μ) /σ) < ( (590 – 600) / 3) )= p ( Z < -10/3) = p( Z < -3.33) = 0.0004

6-標準差(6-sigma或6-σ)的品質管制標準

6-標準差(6-sigma或6-σ)，是製造業流行的品質管制標準。在這個標準之下，一個標準常態分配的變數值出現在正負三個標準差之外，只有2* 0.0013= 0.0026 (p (Z < -3) = 0.0013以及p(Z > 3) = 0.0013)。也就是說，這種品質管制標準的產品不良率只有萬分之二十六。假設例中的飲料公司裝瓶流程採用這個標準，而每罐飲料裝填量符合平均600毫升，標準差3毫升的常態分配。那麼預期裝填容量的範圍應該多少？

6-標準差的範圍 = p ( -3 < Z < 3)= p ( - 3 < (X-μ) /σ < 3) = p ( -3 < (X- 600) / 3 < 3)= p ( -9 < X – 600 < 9) = p (591 < X < 609) 因此，預期裝填容量應該介於591至609毫升之間。

生物標本的物理特性

金融變量

壽命

測試和智力分布

計算學生智商高低的機率

假設某校入學新生的智力測驗平均分數與標準差分別為100與12。那麼隨機抽取50個學生，他們智力測驗平均分數大於105的機率？小於90的機率？

本例沒有常態分配的假設，還好中央極限定理提供一個可行解，那就是當隨機樣本長度超過30，樣本平均數${\displaystyle {\bar {x}}}$近似於一個常態變數，

因此標準常態變數${\displaystyle Z={\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}}$。

平均分數大於105的機率 ${\displaystyle P(Z>{\frac {105-100}{12/{\sqrt {50}}}})=P(Z>5/1.7)=P(Z>2.94)=0.0016}$

平均分數小於90的機率 ${\displaystyle P(Z<{\frac {90-100}{12/{\sqrt {50}}}})=P(Z<-5.88)=0.0000}$

計算統計應用

生成常態分布隨機變數

在計算機模擬中，經常需要生成常態分布的數值。最基本的一個方法是使用標準的常態累積分布函數的反函數。除此之外還有其他更加高效的方法，Box-Muller轉換就是其中之一。另一個更加快捷的方法是ziggurat算法。下面將介紹這兩種方法。一個簡單可行的並且容易編程的方法是：求12個在（0,1）上均勻分布的和，然後減6(12的一半)。這種方法可以用在很多應用中。這12個數的和是Irwin-Hall分布；選擇一個變異數12。這個隨即推導的結果限制在（-6,6）之間，並且密度為12，是用11次多項式估計常態分布。

Box-Muller方法是以兩組獨立的隨機數U和V，這兩組數在(0,1]上均勻分布，用U和V生成兩組獨立的標準常態分布隨機變數X和Y:

${\displaystyle X={\sqrt {-2\ln U}}\,\cos(2\pi V),}$

${\displaystyle Y={\sqrt {-2\ln U}}\,\sin(2\pi V)}$。

這個方程式的提出是因為二自由度的卡方分布（見性質4）很容易由指數隨機變數（方程式中的lnU）生成。因而通過隨機變數V可以選擇一個均勻環繞圓圈的角度，用指數分布選擇半徑然後轉換成（常態分布的）x,y坐標。

參考文獻

1. 物理學名詞審定委員會．物理學名詞 [S/OL]．全國科學技術名詞審定委員會,公布. 3版．北京：科學出版社, 2019: 12. 科學文庫 （頁面存檔備份，存於網際網路檔案館）.
2. Normal Distribution （頁面存檔備份，存於網際網路檔案館）, Gale Encyclopedia of Psychology
3. Casella & Berger (2001，第102頁) harvtxt模板錯誤: 無指向目標: CITEREFCasellaBerger2001 (幫助)
4. McPherson (1990，第110頁) harvtxt模板錯誤: 無指向目標: CITEREFMcPherson1990 (幫助)
5. Shaou-Gang Miaou; Jin-Syan Chou. 《Fundamentals of probability and statistics》. 高立圖書. 2012: 第147頁. ISBN 9789864128990. 引文使用過時母數coauthors (幫助)

• John Aldrich. Earliest Uses of Symbols in Probability and Statistics.網上材料，2006年6月3日存在.(See "Symbols associated with the Normal Distribution".)
• Abraham de Moivre (1738年). The Doctrine of Chances.
• Stephen Jay Gould (1981年). The Mismeasure of Man. First edition. W. W. Norton. ISBN 978-0-393-01489-1.
• R. J. Herrnstein and Charles Murray (1994年). The Bell Curve: Intelligence and Class Structure in American Life. Free Press. ISBN 978-0-02-914673-6.
• Pierre-Simon Laplace (1812年). Analytical Theory of Probabilities.
• Jeff Miller, John Aldrich, et al. Earliest Known Uses of Some of the Words of Mathematics. In particular, the entries for "bell-shaped and bell curve", "normal" (distribution), "Gaussian", and "Error, law of error, theory of errors, etc.".網上材料，2006年6月3日存在
• S. M. Stigler (1999年). Statistics on the Table, chapter 22. Harvard University Press. (History of the term "normal distribution".)
• Eric W. Weisstein et al. Normal Distribution （頁面存檔備份，存於網際網路檔案館） at MathWorld.網上材料，2006年6月3日存在。
• Marvin Zelen and Norman C. Severo (1964年). Probability Functions. Chapter 26 of Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, ed, by Milton Abramowitz and Irene A. Stegun. National Bureau of Standards.

外部連結

• Interactive Distribution Modeler (incl. Normal Distribution) （頁面存檔備份，存於網際網路檔案館）.
• basic tools for sixsigma （頁面存檔備份，存於網際網路檔案館）
• PlanetMath: normal random variable （頁面存檔備份，存於網際網路檔案館）
• GNU Scientific Library – Reference Manual – The Gaussian Distribution （頁面存檔備份，存於網際網路檔案館）
• Distribution Calculator （頁面存檔備份，存於網際網路檔案館） – Calculates probabilities and critical values for normal, t, chi-square and F-distribution.
• Inverse Cumulative Standard Normal Distribution Function
• Is normal distribution due to Karl Gauss? Euler, his family of gamma functions, and place in history of statistics
• Maxwell demons: Simulating probability distributions with functions of propositional calculus
• Normal distribution table （頁面存檔備份，存於網際網路檔案館）
• The Doctrine of Chance （頁面存檔備份，存於網際網路檔案館） at MathPages.
• 常態分布的前世今生(上)
• 常態分布的前世今生(下)
• 在線計算器 常態分布 （頁面存檔備份，存於網際網路檔案館）
• Binomial Distribution Calculator （頁面存檔備份，存於網際網路檔案館）

參見

• 數學主題
• 統計學主題

• 中央極限定理
• 機率論
• 伽瑪分布