互補誤差函數 ,記為 erfc,在誤差函數的基礎上定義:
erfc
(
x
)
=
1
−
erf
(
x
)
=
2
π
∫
x
∞
e
−
t
2
d
t
.
{\displaystyle {\mbox{erfc}}(x)=1-{\mbox{erf}}(x)={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t\,.}
虛誤差函數 ,記為 erfi ,定義為:
erfi
(
z
)
=
−
i
erf
(
i
z
)
.
{\displaystyle \operatorname {erfi} (z)=-i\,\,\operatorname {erf} (i\,z).}
複誤差函數 ,記為w (z ),也在誤差函數的基礎上定義:
w
(
z
)
=
e
−
z
2
erfc
(
−
i
z
)
.
{\displaystyle w(z)=e^{-z^{2}}{\textrm {erfc}}(-iz).}
誤差函數來自測度論 ,後來與測量 誤差無關的其他領域也用到這一函數,但仍然使用誤差函數這一名字。
誤差函數與標準常態分布 的積分累積分布函數
Φ
{\displaystyle \Phi }
[ 2]
Φ
(
x
)
=
1
2
+
1
2
erf
(
x
2
)
.
{\displaystyle \Phi (x)={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right).}
誤差函數是奇函數 :
erf
(
−
z
)
=
−
erf
(
z
)
{\displaystyle \operatorname {erf} (-z)=-\operatorname {erf} (z)}
對於任何 複數 z :
erf
(
z
¯
)
=
erf
(
z
)
¯
{\displaystyle \operatorname {erf} ({\overline {z}})={\overline {\operatorname {erf} (z)}}}
其中
z
¯
{\displaystyle {\overline {z}}}
z 的 複共軛 。
複數平面上,函數 ƒ = exp(−z 2 ) 和 ƒ = erf(z ) 如圖所示。粗綠線表示 Im(ƒ ) = 0,粗紅線表示 Im(ƒ ) < 0, 粗藍線為 Im(ƒ ) > 0。細綠線表示 Im(ƒ ) = constant,細紅線表示 Re(ƒ ) = constant<0,細藍線表示 Re(ƒ ) = constant>0。
在實數軸上, z → ∞時,erf(z ) 趨於1,z → −∞時,erf(z ) 趨於−1 。在虛數軸上, erf(z ) 趨於 ±i∞。
誤差函數是整函數 ,沒有奇異點(無窮遠處除外),泰勒展開收斂。
誤差函數泰勒級數:
erf
(
z
)
=
2
π
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
n
!
(
2
n
+
1
)
=
2
π
(
z
−
z
3
3
+
z
5
10
−
z
7
42
+
z
9
216
−
⋯
)
{\displaystyle \operatorname {erf} (z)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\ \cdots \right)}
對每個複數 z 均成立。
上式可以用迭代形式表示:
erf
(
z
)
=
2
π
∑
n
=
0
∞
(
z
∏
k
=
1
n
−
(
2
k
−
1
)
z
2
k
(
2
k
+
1
)
)
=
2
π
∑
n
=
0
∞
z
2
n
+
1
∏
k
=
1
n
−
z
2
k
{\displaystyle \operatorname {erf} (z)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}}
誤差函數的導數 :
d
d
z
e
r
f
(
z
)
=
2
π
e
−
z
2
.
{\displaystyle {\frac {\rm {d}}{{\rm {d}}z}}\,\mathrm {erf} (z)={\frac {2}{\sqrt {\pi }}}\,e^{-z^{2}}.}
誤差函數的 不定積分 為:
z
erf
(
z
)
+
e
−
z
2
π
{\displaystyle z\,\operatorname {erf} (z)+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}}
逆誤差函數 逆誤差函數 可由 麥克勞林級數 表示:
erf
−
1
(
z
)
=
∑
k
=
0
∞
c
k
2
k
+
1
(
π
2
z
)
2
k
+
1
,
{\displaystyle \operatorname {erf} ^{-1}(z)=\sum _{k=0}^{\infty }{\frac {c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}z\right)^{2k+1},\,\!}
其中, c 0 = 1 ,
c
k
=
∑
m
=
0
k
−
1
c
m
c
k
−
1
−
m
(
m
+
1
)
(
2
m
+
1
)
=
{
1
,
1
,
7
6
,
127
90
,
4369
2520
,
…
}
.
{\displaystyle c_{k}=\sum _{m=0}^{k-1}{\frac {c_{m}c_{k-1-m}}{(m+1)(2m+1)}}=\left\{1,1,{\frac {7}{6}},{\frac {127}{90}},{\frac {4369}{2520}},\ldots \right\}.}
即:
erf
−
1
(
z
)
=
1
2
π
(
z
+
π
12
z
3
+
7
π
2
480
z
5
+
127
π
3
40320
z
7
+
4369
π
4
5806080
z
9
+
34807
π
5
182476800
z
11
+
⋯
)
.
{\displaystyle \operatorname {erf} ^{-1}(z)={\tfrac {1}{2}}{\sqrt {\pi }}\left(z+{\frac {\pi }{12}}z^{3}+{\frac {7\pi ^{2}}{480}}z^{5}+{\frac {127\pi ^{3}}{40320}}z^{7}+{\frac {4369\pi ^{4}}{5806080}}z^{9}+{\frac {34807\pi ^{5}}{182476800}}z^{11}+\cdots \right).\ }
逆互補誤差函數 定義為:
erfc
−
1
(
1
−
z
)
=
erf
−
1
(
z
)
.
{\displaystyle \operatorname {erfc} ^{-1}(1-z)=\operatorname {erf} ^{-1}(z).}
互補誤差函數的漸近展開 ,
e
r
f
c
(
x
)
=
e
−
x
2
x
π
[
1
+
∑
n
=
1
∞
(
−
1
)
n
1
⋅
3
⋅
5
⋯
(
2
n
−
1
)
(
2
x
2
)
n
]
=
e
−
x
2
x
π
∑
n
=
0
∞
(
−
1
)
n
(
2
n
−
1
)
!
!
(
2
x
2
)
n
,
{\displaystyle \mathrm {erfc} (x)={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left[1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{(2x^{2})^{n}}}\right]={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{(2x^{2})^{n}}},\,}
其中 (2n – 1)!! 為 雙階乘 ,x 為實數,該級數對有限 x 發散。對於
N
∈
N
{\displaystyle N\in \mathbb {N} }
e
r
f
c
(
x
)
=
e
−
x
2
x
π
∑
n
=
0
N
−
1
(
−
1
)
n
(
2
n
−
1
)
!
!
(
2
x
2
)
n
+
R
N
(
x
)
{\displaystyle \mathrm {erfc} (x)={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{N-1}(-1)^{n}{\frac {(2n-1)!!}{(2x^{2})^{n}}}+R_{N}(x)\,}
其中餘項用以 大O符號 表示為
R
N
(
x
)
=
O
(
x
−
2
N
+
1
e
−
x
2
)
{\displaystyle R_{N}(x)=O(x^{-2N+1}e^{-x^{2}})}
x
→
∞
{\displaystyle x\to \infty }
餘項的精確形式為:
R
N
(
x
)
:=
(
−
1
)
N
π
2
−
2
N
+
1
(
2
N
)
!
N
!
∫
x
∞
t
−
2
N
e
−
t
2
d
t
,
{\displaystyle R_{N}(x):={\frac {(-1)^{N}}{\sqrt {\pi }}}2^{-2N+1}{\frac {(2N)!}{N!}}\int _{x}^{\infty }t^{-2N}e^{-t^{2}}\,\mathrm {d} t,}
對於比較大的 x, 只需漸近展開中開始的幾項就可以得到 erfc(x )很好的近似值。[ 註 3]
互補誤差函數的連分式展開形式:[ 3]
e
r
f
c
(
z
)
=
z
π
e
−
z
2
a
1
z
2
+
a
2
1
+
a
3
z
2
+
a
4
1
+
⋯
a
1
=
1
,
a
m
=
m
−
1
2
,
m
≥
2.
{\displaystyle \mathrm {erfc} (z)={\frac {z}{\sqrt {\pi }}}e^{-z^{2}}{\cfrac {a_{1}}{z^{2}+{\cfrac {a_{2}}{1+{\cfrac {a_{3}}{z^{2}+{\cfrac {a_{4}}{1+\dotsb }}}}}}}}\qquad a_{1}=1,\quad a_{m}={\frac {m-1}{2}},\quad m\geq 2.}
erf
(
x
)
≈
1
−
1
(
1
+
a
1
x
+
a
2
x
2
+
a
3
x
3
+
a
4
x
4
)
4
{\displaystyle \operatorname {erf} (x)\approx 1-{\frac {1}{(1+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4})^{4}}}}
−4 )其中, a 1 = 0.278393, a 2 = 0.230389, a 3 = 0.000972, a 4 = 0.078108
erf
(
x
)
≈
1
−
(
a
1
t
+
a
2
t
2
+
a
3
t
3
)
e
−
x
2
,
t
=
1
1
+
p
x
{\displaystyle \operatorname {erf} (x)\approx 1-(a_{1}t+a_{2}t^{2}+a_{3}t^{3})e^{-x^{2}},\quad t={\frac {1}{1+px}}}
−5 )其中, p = 0.47047, a 1 = 0.3480242, a 2 = −0.0958798, a 3 = 0.7478556
erf
(
x
)
≈
1
−
1
(
1
+
a
1
x
+
a
2
x
2
+
⋯
+
a
6
x
6
)
16
{\displaystyle \operatorname {erf} (x)\approx 1-{\frac {1}{(1+a_{1}x+a_{2}x^{2}+\cdots +a_{6}x^{6})^{16}}}}
−7 )其中, a 1 = 0.0705230784, a 2 = 0.0422820123, a 3 = 0.0092705272, a 4 = 0.0001520143, a 5 = 0.0002765672, a 6 = 0.0000430638
erf
(
x
)
≈
1
−
(
a
1
t
+
a
2
t
2
+
⋯
+
a
5
t
5
)
e
−
x
2
,
t
=
1
1
+
p
x
{\displaystyle \operatorname {erf} (x)\approx 1-(a_{1}t+a_{2}t^{2}+\cdots +a_{5}t^{5})e^{-x^{2}},\quad t={\frac {1}{1+px}}}
−7 )其中, p = 0.3275911, a 1 = 0.254829592, a 2 = −0.284496736, a 3 = 1.421413741, a 4 = −1.453152027, a 5 = 1.061405429
以上所有近似式適用範圍是: x ≥ 0. 對於負的 x , 誤差函數是奇函數這一性質得到誤差函數的值, erf(x ) = −erf(−x ).
另有近似式:
erf
(
x
)
≈
sgn
(
x
)
1
−
exp
(
−
x
2
4
/
π
+
a
x
2
1
+
a
x
2
)
{\displaystyle \operatorname {erf} (x)\approx \operatorname {sgn}(x){\sqrt {1-\exp \left(-x^{2}{\frac {4/\pi +ax^{2}}{1+ax^{2}}}\right)}}}
其中,
a
=
8
(
π
−
3
)
3
π
(
4
−
π
)
≈
0.140012.
{\displaystyle a={\frac {8(\pi -3)}{3\pi (4-\pi )}}\approx 0.140012.}
該近似式在0或無窮的鄰域非常準確,x 整個定義域上,近似式最大誤差小於0.00035,取 a ≈ 0.147 ,最大誤差可減小到0.00012。[ 4]
逆誤差函數近似式:
erf
−
1
(
x
)
≈
sgn
(
x
)
(
2
π
a
+
ln
(
1
−
x
2
)
2
)
2
−
ln
(
1
−
x
2
)
a
−
(
2
π
a
+
ln
(
1
−
x
2
)
2
)
.
{\displaystyle \operatorname {erf} ^{-1}(x)\approx \operatorname {sgn}(x){\sqrt {{\sqrt {\left({\frac {2}{\pi a}}+{\frac {\ln(1-x^{2})}{2}}\right)^{2}-{\frac {\ln(1-x^{2})}{a}}}}-\left({\frac {2}{\pi a}}+{\frac {\ln(1-x^{2})}{2}}\right)}}.}
誤差函數本質上與標準常態累積分布函數
Φ
{\displaystyle \Phi }
Φ
(
x
)
=
1
2
π
∫
−
∞
x
e
−
t
2
2
d
t
=
1
2
[
1
+
erf
(
x
2
)
]
=
1
2
erfc
(
−
x
2
)
{\displaystyle \Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]={\frac {1}{2}}\,\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)}
可整理為如下形式:
e
r
f
(
x
)
=
2
Φ
(
x
2
)
−
1
e
r
f
c
(
x
)
=
2
Φ
(
−
x
2
)
=
2
(
1
−
Φ
(
x
2
)
)
.
{\displaystyle {\begin{aligned}\mathrm {erf} (x)&=2\Phi \left(x{\sqrt {2}}\right)-1\\\mathrm {erfc} (x)&=2\Phi \left(-x{\sqrt {2}}\right)=2\left(1-\Phi \left(x{\sqrt {2}}\right)\right).\end{aligned}}}
Φ
{\displaystyle \Phi }
分位函數 ,即機率單位
probit
(
p
)
=
Φ
−
1
(
p
)
=
2
erf
−
1
(
2
p
−
1
)
=
−
2
erfc
−
1
(
2
p
)
.
{\displaystyle \operatorname {probit} (p)=\Phi ^{-1}(p)={\sqrt {2}}\,\operatorname {erf} ^{-1}(2p-1)=-{\sqrt {2}}\,\operatorname {erfc} ^{-1}(2p).}
誤差函數為標準常態分布的尾機率Q函數
Q
(
x
)
=
1
2
−
1
2
erf
(
x
2
)
=
1
2
erfc
(
x
2
)
.
{\displaystyle Q(x)={\frac {1}{2}}-{\frac {1}{2}}\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)={\frac {1}{2}}\operatorname {erfc} \left({\frac {x}{\sqrt {2}}}\right).}
誤差函數是米塔-列夫勒函數 的特例,可以表示為合流超幾何函數 ,
e
r
f
(
x
)
=
2
x
π
1
F
1
(
1
2
,
3
2
,
−
x
2
)
.
{\displaystyle \mathrm {erf} (x)={\frac {2x}{\sqrt {\pi }}}\,_{1}F_{1}\left({\tfrac {1}{2}},{\tfrac {3}{2}},-x^{2}\right).}
誤差函數用正則Γ函數 P和 不完全Γ函數 表示為
erf
(
x
)
=
sgn
(
x
)
P
(
1
2
,
x
2
)
=
sgn
(
x
)
π
γ
(
1
2
,
x
2
)
.
{\displaystyle \operatorname {erf} (x)=\operatorname {sgn} (x)P\left({\tfrac {1}{2}},x^{2}\right)={\operatorname {sgn} (x) \over {\sqrt {\pi }}}\gamma \left({\tfrac {1}{2}},x^{2}\right).}
sgn
(
x
)
{\displaystyle \scriptstyle \operatorname {sgn} (x)\ }
符號函數 .
廣義誤差函數圖像 E n (x ):E 1 (x ) = (1 − e −x )/
π
{\displaystyle \scriptstyle {\sqrt {\pi }}}
E 2 (x ) = erf(x )E 3 (x )E 4 (x )E 5 (x ). 廣義誤差函數為:
E
n
(
x
)
=
n
!
π
∫
0
x
e
−
t
n
d
t
=
n
!
π
∑
p
=
0
∞
(
−
1
)
p
x
n
p
+
1
(
n
p
+
1
)
p
!
.
{\displaystyle E_{n}(x)={\frac {n!}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{n}}\,\mathrm {d} t={\frac {n!}{\sqrt {\pi }}}\sum _{p=0}^{\infty }(-1)^{p}{\frac {x^{np+1}}{(np+1)p!}}\,.}
其中,E 0 (x )為通過原點的直線,
E
0
(
x
)
=
x
e
π
{\displaystyle \scriptstyle E_{0}(x)={\frac {x}{e{\sqrt {\pi }}}}}
E 2 (x ) 即為誤差函數 erf(x )。
x > 0時,廣義誤差函數可以用Γ函數和 不完全Γ函數表示,
E
n
(
x
)
=
Γ
(
n
)
(
Γ
(
1
n
)
−
Γ
(
1
n
,
x
n
)
)
π
,
x
>
0.
{\displaystyle E_{n}(x)={\frac {\Gamma (n)\left(\Gamma \left({\frac {1}{n}}\right)-\Gamma \left({\frac {1}{n}},x^{n}\right)\right)}{\sqrt {\pi }}},\quad \quad x>0.\ }
因此,誤差函數可以用不完全Γ函數表示為:
erf
(
x
)
=
1
−
Γ
(
1
2
,
x
2
)
π
.
{\displaystyle \operatorname {erf} (x)=1-{\frac {\Gamma \left({\frac {1}{2}},x^{2}\right)}{\sqrt {\pi }}}.\ }
互補誤差函數的迭代積分定義為:
i
n
erfc
(
z
)
=
∫
z
∞
i
n
−
1
erfc
(
ζ
)
d
ζ
.
{\displaystyle \mathrm {i} ^{n}\operatorname {erfc} \,(z)=\int _{z}^{\infty }\mathrm {i} ^{n-1}\operatorname {erfc} \,(\zeta )\;\mathrm {d} \zeta .\,}
可以展開成冪級數:
i
n
erfc
(
z
)
=
∑
j
=
0
∞
(
−
z
)
j
2
n
−
j
j
!
Γ
(
1
+
n
−
j
2
)
,
{\displaystyle \mathrm {i} ^{n}\operatorname {erfc} \,(z)=\sum _{j=0}^{\infty }{\frac {(-z)^{j}}{2^{n-j}j!\Gamma \left(1+{\frac {n-j}{2}}\right)}}\,,}
滿足如下對稱性質:
i
2
m
erfc
(
−
z
)
=
−
i
2
m
erfc
(
z
)
+
∑
q
=
0
m
z
2
q
2
2
(
m
−
q
)
−
1
(
2
q
)
!
(
m
−
q
)
!
{\displaystyle \mathrm {i} ^{2m}\operatorname {erfc} (-z)=-\mathrm {i} ^{2m}\operatorname {erfc} \,(z)+\sum _{q=0}^{m}{\frac {z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}}}
和
i
2
m
+
1
erfc
(
−
z
)
=
i
2
m
+
1
erfc
(
z
)
+
∑
q
=
0
m
z
2
q
+
1
2
2
(
m
−
q
)
−
1
(
2
q
+
1
)
!
(
m
−
q
)
!
.
{\displaystyle \mathrm {i} ^{2m+1}\operatorname {erfc} (-z)=\mathrm {i} ^{2m+1}\operatorname {erfc} \,(z)+\sum _{q=0}^{m}{\frac {z^{2q+1}}{2^{2(m-q)-1}(2q+1)!(m-q)!}}\,.}
More information x, erf(x) ...
x
erf(x)
erfc(x)
x
erf(x)
erfc(x)
0.00
0.0000000
1.0000000
1.30
0.9340079
0.0659921
0.05
0.0563720
0.9436280
1.40
0.9522851
0.0477149
0.10
0.1124629
0.8875371
1.50
0.9661051
0.0338949
0.15
0.1679960
0.8320040
1.60
0.9763484
0.0236516
0.20
0.2227026
0.7772974
1.70
0.9837905
0.0162095
0.25
0.2763264
0.7236736
1.80
0.9890905
0.0109095
0.30
0.3286268
0.6713732
1.90
0.9927904
0.0072096
0.35
0.3793821
0.6206179
2.00
0.9953223
0.0046777
0.40
0.4283924
0.5716076
2.10
0.9970205
0.0029795
0.45
0.4754817
0.5245183
2.20
0.9981372
0.0018628
0.50
0.5204999
0.4795001
2.30
0.9988568
0.0011432
0.55
0.5633234
0.4366766
2.40
0.9993115
0.0006885
0.60
0.6038561
0.3961439
2.50
0.9995930
0.0004070
0.65
0.6420293
0.3579707
2.60
0.9997640
0.0002360
0.70
0.6778012
0.3221988
2.70
0.9998657
0.0001343
0.75
0.7111556
0.2888444
2.80
0.9999250
0.0000750
0.80
0.7421010
0.2578990
2.90
0.9999589
0.0000411
0.85
0.7706681
0.2293319
3.00
0.9999779
0.0000221
0.90
0.7969082
0.2030918
3.10
0.9999884
0.0000116
0.95
0.8208908
0.1791092
3.20
0.9999940
0.0000060
1.00
0.8427008
0.1572992
3.30
0.9999969
0.0000031
1.10
0.8802051
0.1197949
3.40
0.9999985
0.0000015
1.20
0.9103140
0.0896860
3.50
0.9999993
0.0000007
x
erfc(x)/2
1
7.86496e−2
2
2.33887e−3
3
1.10452e−5
4
7.70863e−9
5
7.6873e−13
6
1.07599e−17
7
2.09191e−23
8
5.61215e−30
9
2.06852e−37
10
1.04424e−45
11
7.20433e−55
12
6.78131e−65
13
8.69779e−76
14
1.51861e−87
15
3.6065e−100
16
1.16424e−113
17
5.10614e−128
18
3.04118e−143
19
2.45886e−159
20
2.69793e−176
21
4.01623e−194
22
8.10953e−213
23
2.22063e−232
24
8.24491e−253
25
4.15009e−274
26
2.8316e−296
27
2.61855e−319
Close
Greene, William H.; Econometric Analysis (fifth edition), Prentice-Hall, 1993, p. 926, fn. 11
Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. Handbook of Continued Fractions for Special Functions. Springer-Verlag . 2008. ISBN 978-1-4020-6948-2 Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 978-0-521-43064-7 ), 1992, page 214, Cambridge University Press. 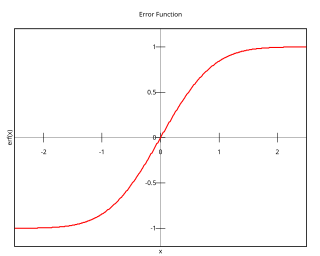























![{\displaystyle \mathrm {erfc} (x)={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left[1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{(2x^{2})^{n}}}\right]={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{(2x^{2})^{n}}},\,}](http://wikimedia.org/api/rest_v1/media/math/render/svg/802266cbf19574e452c0f388f9585fbb5d831064)

















![{\displaystyle \Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]={\frac {1}{2}}\,\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9c1d0724a58c2d7643ac79237496d4f6de3b1e9a)















