扭稜

在幾何學中，扭稜是一種多面體變換。該術語起源於刻卜勒對阿基米德立體的命名，分別為扭棱立方體（英語：snub cube、拉丁語：cubus simus）和扭棱十二面體（英語：snub dodecahedron、拉丁語：dodecaedron simum）^[1][2]。一般而言，多面體經扭稜變換後可以形成兩種互為手性鏡像的形式，分別為順時針方向的扭稜和逆時針方向的扭稜。以刻卜勒的命名對應的扭稜變換可以看做是正多面體的擴張，也就是將正多面體的面向外分開，並圍繞着中心扭曲（不改變面的形狀），然後加入以每個原始立體頂點為中心的正方形，並在每個原始立體之邊的位置上加入成對的三角形來構成。^[3]:99

立方體經由康威扭稜成扭棱立方體過程的動畫

兩種扭稜而成的阿基米德立體

扭棱立方體或 扭稜截半立方體

扭棱十二面體或 扭稜截半十二面體

扭棱立方體的兩種手性鏡像，其為截角截半立方體經交錯變換後的像

透過旋轉小斜方截半立方體的正方形面直到12個白色正方形變成成對的正三角形面即可構造一個扭棱立方體

考克斯特對扭稜進行了推廣，推廣成能用於更廣泛的均勻多面體，其定義略有不同。

康威扭稜

康威研究了廣義的多面體變換，定義了現在稱為康威多面體表示法的多面體變換表示法，其可以運用在多面體和各種鑲嵌或密鋪的幾何形狀。康威稱考克斯特定義的扭稜變換為半扭稜變換。^[5]

在康威多面體表示法中，扭稜變換（康威表示法：s）被定義為陀螺變換（英語：gyro，康威表示法：g，為每個n邊形面被切割成n個五邊形的多面體變換）的對偶多面體（康威表示法：d），即康威表示法s = dg = dgd^[6]，其等價於先經截半變換再做截角變換後進行交替截角。康威表示法本身避免了考克斯特的交錯（半）變換，因為它僅適用於僅具有偶數邊數的面之多面體。

扭稜的正圖形

扭稜的形式	多面體			平面鑲嵌		雙曲鑲嵌
原像名稱	正四面體	立方體或 正八面體	正二十面體或 正十二面體	正方形鑲嵌	正六邊形鑲嵌或 正三角形鑲嵌	正七邊形鑲嵌或 七階三角形鑲嵌
圖像
扭稜結果的康威表示法	sT	sC = sO	sI = sD	sQ	sH = sΔ	sΔ7
圖像	扭稜四面體 （正二十面體）	扭稜立方體	扭稜十二面體	扭稜正方形鑲嵌	扭稜六邊形鑲嵌	扭稜七邊形鑲嵌（英語：Snub triheptagonal tiling）

在四維空間中，康威建議將扭稜二十四胞體（英語：Snub 24-cell）稱為半扭稜二十四胞體。與三維的扭稜多面體不同，三維的扭稜多面體是交替的全截（omnitruncation，即先截半再截角）的形式，而扭稜二十四胞體並非是正二十四胞體交替的全截的形式。事實上，扭稜二十四胞體是交替截角的正二十四胞體^[7]。

考克斯特扭稜

扭稜立方體，衍生自立方體或截半立方體

	原像	截半 r	截角 t	交錯 h
名稱	立方體	截半立方體	截角截半立方體 全截立方體	扭稜截半立方體
康威表示法	C	CO rC	tCO trC或trO	htCO = sCO htrC = srC
施萊夫利符號	{4,3}	${\displaystyle {\begin{Bmatrix}4\\3\end{Bmatrix}}}$或r{4,3}	${\displaystyle t{\begin{Bmatrix}4\\3\end{Bmatrix}}}$或tr{4,3}	${\displaystyle ht{\begin{Bmatrix}4\\3\end{Bmatrix}}=s{\begin{Bmatrix}4\\3\end{Bmatrix}}}$ htr{4,3} = sr{4,3}
考克斯特圖（英語：Coxeter-Dynkin diagram）		或	或	或
圖像

從正八面體經由考克斯特扭稜變換，變換為扭稜八面體的連續動畫

考克斯特扭稜的定義略有不同，其將扭稜定義為截角後交錯，在這個定義下，扭稜立方體被視為扭稜後的截半立方體、扭棱十二面體被視為扭稜後的截半十二面體。在這種定義下命名的詹森多面體有扭稜鍥形體和扭稜四角反角柱。這種命名在高維多胞體中也有所使用，如擴展施萊夫利符號記為s{3,4,3}，並在考克斯特—迪肯符號（英語：Coxeter-Dynkin diagram）記為的扭稜二十四胞體（英語：Snub 24-cell）^[8]。

一個正多面體或鑲嵌若在施萊夫利符號記為${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$且考克斯特—迪肯符號（英語：Coxeter-Dynkin diagram）記為，則其截角後的像施萊夫利符號記為${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}}$、考克斯特—迪肯符號（英語：Coxeter-Dynkin diagram）記為，若再將這個結果進行交錯變換，則其變換後的像施萊夫利符號記為${\displaystyle ht{\begin{Bmatrix}p,q\end{Bmatrix}}=s{\begin{Bmatrix}p,q\end{Bmatrix}}}$、考克斯特—迪肯符號記為。要完成這個交錯變換，q必須為偶數^[9]。

一個擬正多面體若在施萊夫利符號記為${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$或r{p,q}、考克斯特—迪肯符號記為或，則其截角的像施萊夫利符號記為${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}}$或tr{p,q}，則這個擬正多面體的扭稜可以定義為交錯的截角截半立體${\displaystyle ht{\begin{Bmatrix}p\\q\end{Bmatrix}}=s{\begin{Bmatrix}p\\q\end{Bmatrix}}}$或 htr{p,q} = sr{p,q}，和 or 。

例如，以刻卜勒的扭棱立方體是扭稜自擬正的截半立方體，而截半立方體的豎式施萊夫利符號記為${\displaystyle {\begin{Bmatrix}4\\3\end{Bmatrix}}}$^[10]、考克斯特—迪肯符號（英語：Coxeter-Dynkin diagram）記為，所以扭棱立方體的豎式施萊夫利符號記為${\displaystyle s{\begin{Bmatrix}4\\3\end{Bmatrix}}}$^[11]、考克斯特—迪肯符號記為。扭棱立方體亦可以視為經過交錯變換的截角截半立方體，截角截半立方體的豎式施萊夫利符號記為${\displaystyle t{\begin{Bmatrix}4\\3\end{Bmatrix}}}$^[12]、考克斯特—迪肯符號記為。^[13]

頂點分支度為偶數的正多面體也可以進行截角後交錯的扭稜，例如扭稜八面體，施萊夫利符號${\displaystyle s{\begin{Bmatrix}3,4\end{Bmatrix}}}$、考克斯特—迪肯符號，其為交錯的截角八面體施萊夫利符號${\displaystyle t{\begin{Bmatrix}3,4\end{Bmatrix}}}$^[14]、考克斯特—迪肯符號。八面體在這種定義下的扭稜結果稱為偽二十面體，一個拓樸與正二十面體完全相同但具備五角十二面體群對稱性的立體^[15]。

	原像	截角 t	交錯 h
名稱	正八面體	截角八面體	扭稜八面體
康威表示法	O	tO	htO or sO
施萊夫利符號	{3,4}	t{3,4}	ht{3,4} = s{3,4}
考克斯特符號
圖像

考克斯特扭稜也允許將反稜柱的施萊夫利符號定義為${\displaystyle s{\begin{Bmatrix}2\\n\end{Bmatrix}}}$^[16]:403或${\displaystyle s{\begin{Bmatrix}2,2n\end{Bmatrix}}}$，基於n角柱的${\displaystyle t{\begin{Bmatrix}2\\n\end{Bmatrix}}}$或${\displaystyle t{\begin{Bmatrix}2,2n\end{Bmatrix}}}$。其中${\displaystyle {\begin{Bmatrix}2,n\end{Bmatrix}}}$是一個退化的n面形，其可以視為由二角形鑲嵌球面的幾何結構。

扭稜多面形, {2,2p}

圖像
考克斯特 符號（英語：Coxeter-Dynkin diagram）							... ...
施萊夫利 符號	s{2,4}	s{2,6}	s{2,8}	s{2,10}	s{2,12}	s{2,14}	s{2,16}...	s{2,∞}（英語：apeirogonal antiprism）
	sr{2,2} ${\displaystyle s{\begin{Bmatrix}2\\2\end{Bmatrix}}}$	sr{2,3} ${\displaystyle s{\begin{Bmatrix}2\\3\end{Bmatrix}}}$	sr{2,4} ${\displaystyle s{\begin{Bmatrix}2\\4\end{Bmatrix}}}$	sr{2,5} ${\displaystyle s{\begin{Bmatrix}2\\5\end{Bmatrix}}}$	sr{2,6} ${\displaystyle s{\begin{Bmatrix}2\\6\end{Bmatrix}}}$	sr{2,7} ${\displaystyle s{\begin{Bmatrix}2\\7\end{Bmatrix}}}$	sr{2,8}... ${\displaystyle s{\begin{Bmatrix}2\\8\end{Bmatrix}}}$...	sr{2,∞} ${\displaystyle s{\begin{Bmatrix}2\\\infty \end{Bmatrix}}}$
康威 表示法	A2 = T	A3 = O	A4	A5	A6	A7	A8...	A∞

非均勻多面體的扭稜

非均勻多面體也可以扭稜，但需要滿足考克斯特扭稜的條件。考克斯特扭稜只能作用在頂點分支度全為偶數的立體上^[13]。這允許了許多多面體的扭稜，包括了無窮集合的立體。例如：

扭稜雙錐體 sdt{2,p}

扭稜雙四角錐
扭稜雙六角錐

扭稜截半雙錐體 srdt{2,p}

扭稜反角柱 s{2,2p}

圖像				...
名稱	扭稜二角 反角柱	扭稜三角 反角柱	扭稜四角 反角柱	扭稜五角 反角柱
施萊夫利 符號	ss{2,4}	ss{2,6}	ss{2,8}	ss{2,10}...
	ssr{2,2} ${\displaystyle ss{\begin{Bmatrix}2\\2\end{Bmatrix}}}$	ssr{2,3} ${\displaystyle ss{\begin{Bmatrix}2\\3\end{Bmatrix}}}$	ssr{2,4} ${\displaystyle ss{\begin{Bmatrix}2\\4\end{Bmatrix}}}$	ssr{2,5}... ${\displaystyle ss{\begin{Bmatrix}2\\5\end{Bmatrix}}}$

考克斯特的均勻扭稜星形多面體

扭稜均勻星形多面體由其施瓦茨三角形(p q r)構造，具有合理有序的鏡像對稱角，且所有鏡像都處於活動和交替的狀態^[17]。

扭稜的均勻星形多面體

s{3/2,3/2}	s{(3,3,5/2)}	sr{5,5/2}	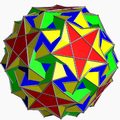s{(3,5,5/3)}	sr{5/2,3}
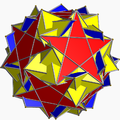sr{5/3,5}	s{(5/2,5/3,3)}	sr{5/3,3}	s{(3/2,3/2,5/2)}	s{3/2,5/3}

參見

• 扭稜多面體（英語：Snub polyhedron）

多面體變換

• 閱
• 論
• 編

原像	截角	截半	過截角	對偶	擴展（英語：Expansion (geometry)）	全截（英語：Omnitruncation）	交錯
							半變換	扭稜
t0{p,q} {p,q}	t01{p,q}（英語：Truncated polyhedron） t{p,q}	t1{p,q} r{p,q}	t12{p,q}（英語：Bitruncated polyhedron） 2t{p,q}	t2{p,q} 2r{p,q}	t02{p,q}（英語：Cantellated polyhedron） rr{p,q}	t012{p,q}（英語：Omnitruncated polyhedron） tr{p,q}	ht0{p,q} h{q,p}	ht12{p,q}（英語：Snub polyhedron） s{q,p}	ht012{p,q}（英語：Snub polyhedron） sr{p,q}