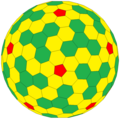
康威多面体表示法
用来表述多面体的方法 来自维基百科,自由的百科全书
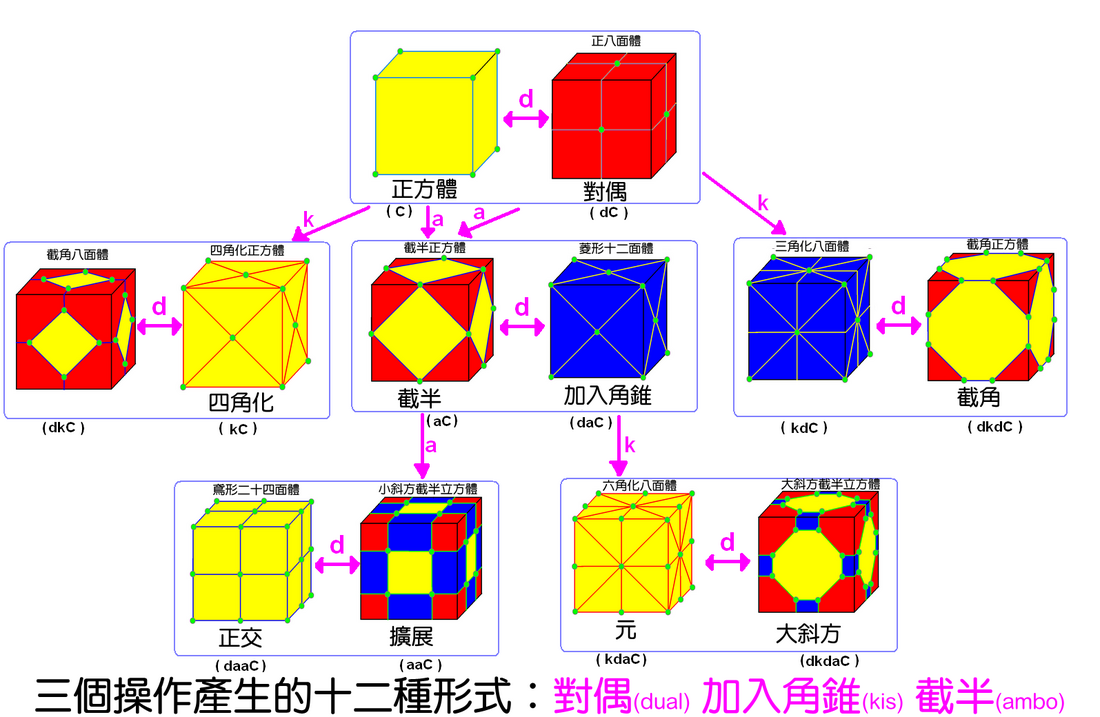
康威多面体表示法是用来描述多面体的一种方法。 一般是用种子多面体(seed)为基础并标示对种子多面体做的操作或运算。

种子多面体一般都为正多面体或正多边形密铺,表示的字母则取他们名字的第一个字母,例如:
- T = 正四面体 (Tetrahedron)
- C = 正方体 (Cube)
- O = 正八面体 (Octahedron)
- D = 正十二面体 (Dodecahedron)
- I = 正二十面体 (Icosahedron)
- H = 正六边形密铺 (Hexagonal tiling)
- Q = 正四边形密铺 (Quadrille = Square tiling)
- Δ = 正三角形密铺 (Deltille = Triangular tiling)
另外柱体和锥体也可以作为种子,并以它是底面边数加一个字母表示:
例如种子“P5”是指五角柱、“P10”是指十角柱、“Y6”是指六角锥、“J86”是指球状屋顶、“A86”是指86角反棱柱。
任何凸多面体皆可以当作种子,前提是它可以执行操作或运算。
何顿·康威提出这个想法, 就像克卜勒的截角定义,建立相关的多面体相同的对称性。 它的多面体表示法能从正多面体种子表示所有阿基米德立体、半正多面体和卡塔兰立体。 在一系列的应用中,康威多面体表示法可以产生许多高阶多面体。
多面体的运算
下面列出康威多面体表示法中,多面体的运算符号,那些运算通常类似几何变换,并以 (v,e,f) 表示进行该运算或操作后多面体的变化。
| 运算符 | 范例 | 运算符号名称 | 别名 | 英文名 | 替代 同构 |
顶点 | 边 | 面 | 描述 | 例子 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 原像 | Seed | v | e | f | 来源种子 | ||||||
| d | 对偶 | dual | f | e | v | 产生对偶多面体-每个顶点创建一个新的面,或面的重心当作新的顶点。 | |||||
| a | 截半 | ambo | e | 2e | 2 + e | 边是新的顶点,旧的顶点消失,或将边的中点当作新的顶点。(rectify) | |||||
| j | 会合 | join | da | e + 2 | 2e | e | 每个面都加入上当高的锥体,使相邻面的锥体各有一面互相共面,形成四边形。 | ||||
| t | 截角 | truncate | dkd | 2e | 3e | e + 2 | 截去所有顶点 conjugate kis |
||||
| k | n角化 | kis | dtd | e + 2 | 3e | 2e | 每个面都加入角锥. | ||||
| i | 过截角 | 双截角 | -- | dk | 2e | 3e | e + 2 | Dual of kis. (bitruncation) | |||
| n | -- | -- | kd | e + 2 | 3e | 2e | Kis of dual | ||||
| e | 小斜方 扩展 |
expand | aa = aj | 2e | 4e | 2e + 2 | 在每个顶点建立新的面,并在各边建立四边形。 (cantellate) | ||||
| o | 正交 | 菱形 鸢形 有时作 四角化 |
ortho | de = ja = jj | 2e + 2 | 4e | 2e | 每个n边形面被分割成n个四边形。 | |||
| b | 大斜方 | bevel | ta | 4e | 6e | 2e + 2 | 加入新的面代替边和顶点 (在高维多胞体称为cantitruncation).) | ||||
| m | 元 |
有时作 三角化 |
meta | db = kj | 2e + 2 | 6e | 4e | 将n边形的面切割成2n个三角形 | |||
| 运算符 | 范例 | 运算符号名称 | 别名 | 英文名 | 替代 同构 |
顶点 | 边 | 面 | 描述 | 例子 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 原像 | Seed | v | e | f | Seed form | ||||||
| r | 手性镜像 | 镜射 | reflect | v | e | f | 产生手性镜像 | ||||
| h | 交错 半* |
half * | v/2 | e | f+v/2 | Alternation, remove half vertices, limited to seed polyhedra with even-sided faces |
|||||
| 部分截半 部分截角 |
uncompleted rectifie/truncate |
e | 2e | 2 + e | 对某些条件面截半,其馀面截角 | tO→ | |||||
| c | 倒角 | chamfer | v + 2e | 4e | f + e | 将边用六边形取代 | T→ | ||||
| 双倒角 | v + 2e | 4e | f + e | 将边用两个五边形取代 | |||||||
| - | - | dc | f + e | 4e | v + 2e | ||||||
| p | 旋转 | propellor (Hart) |
v + 2e | 4e | f + e | 将面旋转,并在顶点建立四边形 (self-dual) | |||||
| - | - | dp = pd | f + e | 4e | v + 2e | ||||||
| s | 扭棱 | snub | dg = hta | 2e | 5e | 3e + 2 | “扩大和扭曲” - 每个顶点创建一个面,每条边创建了两个新的三角形 | ||||
| g | 陀螺 | gyro | ds | 3e + 2 | 5e | 2e | 每个n边形面被切割成n个五边形。 | ||||
| w | 旋面 | whirl | v+4e | 7e | f+2e | 将面旋转,并在顶点建立与原面相似但是旋转的新面 此操作会在边上建立两个六边形 |
|||||
| - | - | dw | f+2e | 7e | v+4e | 旋面的对偶 | |||||
这些运算符号的运算优先顺序皆为由右至左。例如:
所有的操作都保有对称性,除了s和g是扭曲的像并失去了镜射对称。
例子
| 正方体 "seed" |
截半 |
截角 | 双截角(Bitruncation) | 离面 (Cantellation) |
大斜方截半 (Omnitruncation) |
扭棱(Snub) |
|---|---|---|---|---|---|---|
 C |
 aC = djC |
 tC = dkdC |
 tdC = dkC |
 eC = aaC = doC |
 bC = taC = dmC = dkjC |
 sC = dgC |
| 对偶 | 加入锥体 (相邻共面) |
加入锥体 (到外接球) |
正交 (edge-bisect) |
元 (full-bisect) |
陀螺 | |
 dC |
 jC = daC |
 kdC = dtC |
 kC = dtdC |
 oC = deC = daaC |
 mC = dbC = kjC |
 gC = dsC |
生成标准种子
所有的五个正多面体皆可以从棱柱种子经过零至两个运算或操作而产生:
康威的符号扩展
上述的运算和操作可以从正多面体种子或柱体锥体的种子产生所有的半正多面体、卡塔兰立体、柏拉图立体和阿基米德立体。 许多多面体都可由高阶的组合操作还表示,但是某些特别的多面体需要更多的符号来表示。
例如,几何艺术家George W. Hart定义他的操作称为"propellor",和另一个反映创建镜像图像的旋转形式"reflect"。
- p – "propellor" – 旋转建立四边形于顶点。这个操作的对偶多面体是本身: dpX=pdX。
- r – "reflect" – 对种子进行镜射变换。一般没已影响,除非有s或g的种子
詹森多面体扩展
为了表达詹森多面体,诺曼·詹森也定义了一些符号来表达它的多面体[1]
- 下列种子都必须要在后面加注边数:
- 扩展的符号:
- + = 将符号后的种子加到符号前的种子之适当的面,可省略
- - = 在符号前的种子上照到跟符号后种子相同的部分并切除之
- × = 将符号前动作做符号后的次数次,符号后必为常数,可省略
- () = 将种子括号并指定动作
- 例如:
下面扩展符号也可以用于康威多面体表示法,但是在施莱夫利符号中,更为常用。
- t0,1 = 截角
- t0,2 = 截边:小斜方截半
- t0,1,2 = 截边再截角:大斜方截半
- t0,3 = 截面:向下锯齿(Runcination) : 切割多面体,同时沿面、边和顶点,建立新的面代替原来的面、边和顶点中心。
- t0,1,3 = 截面再截角
- t0,2,3 = 截面再截边
- t0,1,2,3 = 截面再截边再截角
- t0,4 = 截胞 : 切割多胞体,同时沿胞、面、边和顶点,建立新的胞代替原来的胞、面、边和顶点中心。
- t1 = 截半
- t1,2 = 截半再截边:双截角
- t2
- h = 交替 alternate
例如:
- "hC" = 正四面体
几何座标的衍生形式
 D |
 tD |
 aD |
 tdD |
 eD |
 teD |
 sD |
 dD |
 dteD |
 H |
 tH |
 aH |
 tdH = H |
 eH |
 teH |
 sH |
 dH |
 dtH |
 daH |
 dtdH = dH |
 deH |
 dteH |
 dsH |
 T |
 tT |
 aT |
 tdT |
 eT |
 bT |
 sT |
 dT |
 dtT |
 jT |
 kT |
 oT |
 mT |
 gT |
 {4,3,3} |
 t{4,3,3} |
 a{4,3,3} |
 td{4,3,3} |
 e{4,3,3} |
 b{4,3,3} |
 s{4,3,3} |
 d{4,3,3} |
其他多面体
迭代简单简单操作的形式,可以产生更大的多面体,并保持基本对称性。顶点被假设是对相同半径的球面。
-
截角三角化四面体
"t6dtT"
-
菱形九十面体
"dakD"
-
五角化十二面体
"kD" -
五角化截半二十面体
"k5aD" -
"k6k5tI"
-
六角化五角化倒角十二面体
"kt5daD" -
"kdktI"
"dtktI" -
"kdkt5daD"
-
截角二十面体
"dkD" -
"dk6k5tI"
-
"dkt5daD"
-
"tktI"
-
"tkt5daD"
参见
外部链接和参考文献
Wikiwand - on
Seamless Wikipedia browsing. On steroids.