截角超立方體

截角超立方體有24個胞:8個截角立方體，和16個正四面體。

截角超立方體
施萊格爾投影 (可以看見正四面體胞)
類型	均勻多胞體
識別
名稱	截角超立方體
參考索引	12 13 14
數學表示法
考克斯特符號 （英語：Coxeter-Dynkin diagram）
施萊夫利符號	t0,1{4,3,3}
性質
胞	24 8 3.8.8 16 3.3.3
面	88 64 {3} 24 {8}
邊	128
頂點	64
組成與佈局
頂點圖	Isosceles triangular pyramid
對稱性
考克斯特群	BC4, [4,3,3], order 384
特性
convex
閱 論 編

坐標

截角超立方體可以通過在每條棱距離頂點${\displaystyle 1/({\sqrt {2}}+2)}$處截斷超立方體的每一個角來得到。每個截斷的角會產生一個正四面體。

一個棱長為2的截角超立方體的每個頂點的笛卡兒坐標系坐標為:

${\displaystyle \left(\pm 1,\ \pm (1+{\sqrt {2}}),\ \pm (1+{\sqrt {2}}),\ \pm (1+{\sqrt {2}})\right)}$

投影

正交投影

考克斯特平面	B4	B3 / D4 / A2	B2 / D3
Graph
二面體群	[8]	[6]	[4]
考克斯特平面	F4	A3
Graph
二面體群	[12/3]	[4]

展開圖

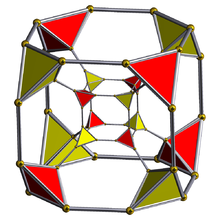
三維正交投影

參考文獻

• T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
• H.S.M. Coxeter:
  • Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] （頁面存檔備份，存於互聯網檔案館）
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
• 2. Convex uniform polychora based on the tesseract (8-cell) and hexadecachoron (16-cell) - Models 13, 16, 17, George Olshevsky.
• Klitzing, Richard. 4D uniform polytopes (polychora). bendwavy.org. o3o3o4o - tat, o3x3x4o - tah, x3x3o4o - thex

外部連結

• Paper model of truncated tesseract （頁面存檔備份，存於互聯網檔案館） created using nets generated by Stella4D software