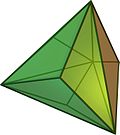
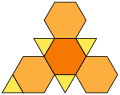
在几何学中,截角四面体是一种半正八面体,13种阿基米德立体之一,共有8个面、18个边和12个顶点,是三角化四面体的对偶多面体,可由四面体经过适当的截角,截去四面体的四个顶点所产生的多面体。
若进行更深的截角,甚至截到了中点,则称为截半四面体,然而此种多面体与正八面体是等价的[1]。
由于截角四面体具有六边形与三角形的面,因此也是一种戈德堡多面体,其戈德堡符号计为GIII(1,1)。
此外,由于截角四面体可以由立方体透过斜截变换构成,即先交错、再截角,因此,截角四面体又称为斜截立方体或截角交错立方体,在考克斯特符号中计为![]()
![]()
![]()
![]()
![]() ,顶点数为小斜方截半立方体
,顶点数为小斜方截半立方体![]()
![]()
![]()
![]()
![]() 的一半,因此两个截角四面体可以构成一个凸包为小斜方截半立方体的截角星形八面体,此种立体也称为二复合截角四面体。[2]
的一半,因此两个截角四面体可以构成一个凸包为小斜方截半立方体的截角星形八面体,此种立体也称为二复合截角四面体。[2]
性质
截角四面体是半正多面体之一,由4个等边三角形和4个正六边形组成,有12个顶点和18条棱,可以想象为将正四面体的顶点切去。
在直角坐标系中,将几何中心位于原点边长为的四面体截角产生了12个顶点,以(±3, ±1, ±1),(±1, ±3, ±1),(±1, ±1, ±3) (其中每组坐标的±数目都是奇数个)为顶点,构成了一个截角四面体。12个顶点位置如下:
- (+3,+1,+1), (+1,+3,+1), (+1,+1,+3)
- (−3,−1,+1), (−1,−3,+1), (−1,−1,+3)
- (−3,+1,−1), (−1,+3,−1), (−1,+1,−3)
- (+3,−1,−1), (+1,−3,−1), (+1,−1,−3)
|

|

|
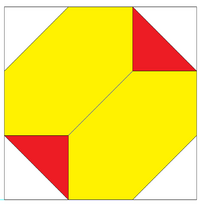
| 正交投影显示截角四面体可置于一个(±3,±3,±3)的边框内。 | 截角四面体的六边形面可分割为6共面的正三角形。其产生了四个新顶点 : (-1,-1,-1), (-1,+1,+1), (+1,-1,+1), (+1,+1,-1). |
顶点(±1,±1,±3)的全排列产生了两个互补的截角四面体,可将之结合成一个复合多面体,即截角星形八面体。 |
边长为的截角四面体,其表面积为,体积为。[3]
- 三角形与六边形的交角:,约为109.47122063449069136924599933996°
- 六边形与六边形的交角:,约为70.528779365509308630754000660038°
- 两个六边形的共线与三角形的交角:,约为125.26438968275465431537700033002°
作法
正交投影
| 中心 | 标准边 | 标准面 | 边 | 面/顶点 |
|---|---|---|---|---|
| 图像 | 
|

|

|

|
| 对偶图像 | 
|

|

|

|
| 投影 对称群 |
[1] | [1] | [3] | [4] |
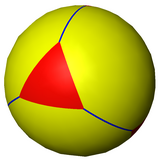
球面镶嵌
相关多面体及镶嵌

|
轨形 *n32 |
球面镶嵌 | 欧氏镶嵌 | 双曲镶嵌 | 仿紧 | ||
|---|---|---|---|---|---|---|---|
| *332 | *333 | *433 | *533 | *633... | *∞33 | ||
| 斜截镶嵌 | 
|

|

|

|

|

| |
| 顶点 | 3.6.2.6 | 3.6.3.6 | 3.6.4.6 | 3.6.5.6 | 3.6.6.6 | 3.6.∞.6 | |

三角化截角四面体为截角四面体进行三角化变换的结果,即将截角四面体的三角形面加入三角锥。
三角化变换是一种克利多面体变换,意指在多面体表面叠上锥体,关于截角四面体的另外一种克利多面体变换则是在六边形面加入六角锥,所构成的立体为六角化截角四面体。
截角四面体图
在图论的数学领域中,与截角四面体相关的图为截角四面体图,其与截角四面体有相同的拓朴结构,是一种阿基米德图[5][6],其顶点与边的数量及结构都与阿基米德立体中的截角四面体相同,具有12个顶点和18个边[7]。属于连结立体图(英语:connected cubic graph)[8],也是一种连结立体可递的图[9]。
参见
参考文献
外部链接
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.