在几何学中，三角化三角形镶嵌（英语：Triakis triangular tiling）是一种平面镶嵌，密铺于欧几里得平面。三角化三角形镶嵌是将三角形镶嵌中的每一个正三角形从重心分割为三个全等的钝角等腰三角形所组成的镶嵌，其分割出来的三角形角度为30-30-120。其面的布局以符号V3.12.12表示，每一个等腰三角形面有两种类型的顶点：其中一个是三个三角形的公共顶点，另外一个是十二个三角形的公共顶点。
康威称三角化三角形镶嵌为kisdeltile[1]，因为它可以从三角形镶嵌（deltille）透过三角化变换构造而得。
在日本，此种模式被称为asanoha（日语：麻の葉、あさのは），其义为大麻叶，然而该名称也适用于其它三角化形状，例如三角化二十面体和三角化八面体[2]。
对偶镶嵌
三角化三角形镶嵌的对偶镶嵌是由正三角形和正十二边形组成的截角六边形镶嵌[3]
相关多面体与镶嵌
三角化三角形镶嵌是一系列截角多面体或镶嵌的对偶之一，该系列从球面到平面一直延伸至双曲平面。他们皆为面可递，并具有(*n32)反射对称。
对称性 *n32[n,3] |
球面 | 欧氏镶嵌 | 紧凑型双曲镶嵌 | 仿紧型镶嵌 | 非紧型镶嵌 | ||||
|---|---|---|---|---|---|---|---|---|---|
| *232 [2,3] D3h |
*332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] P6m |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[iπ/λ,3] | |
| 截角顶点布局 |  3.4.4 |
 3.6.6 |
 3.8.8 |
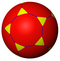 3.10.10 |
 3.12.12 |
 3.14.14 |
 3.16.16 |
 3.∞.∞ |
 3.∞.∞ |
| 考克斯特纪号 施莱夫利符号 |
    t{2,3} |
t{3,3} |
 t{4,3} |
 t{5,3} |
 t{6,3} |
 t{7,3} |
 t{8,3} |
 t{∞,3} |
 t{∞,3} |
| 半正对偶图 | |||||||||
| 三角化 顶点布局 |
 V3.4.4 |
 V3.6.6 |
 V3.8.8 |
 V3.10.10 |
 V3.12.12 |
 V3.14.14 |
 V3.16.16 |
 V3.∞.∞ |
V3.∞.∞ |
| 考克斯特纪号 | 
|
|
|
|
|
|
|
|
|
三角化三角形镶嵌是截角六边形镶嵌的对偶镶嵌，而截角六边形镶嵌是正六边形镶嵌通过截角操作得到的半正镶嵌，其与正六边形镶嵌拥有相似的对称性：
参见
参考文献
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
