热门问题
时间线
聊天
视角
菱形十二面体
来自维基百科,自由的百科全书
Remove ads
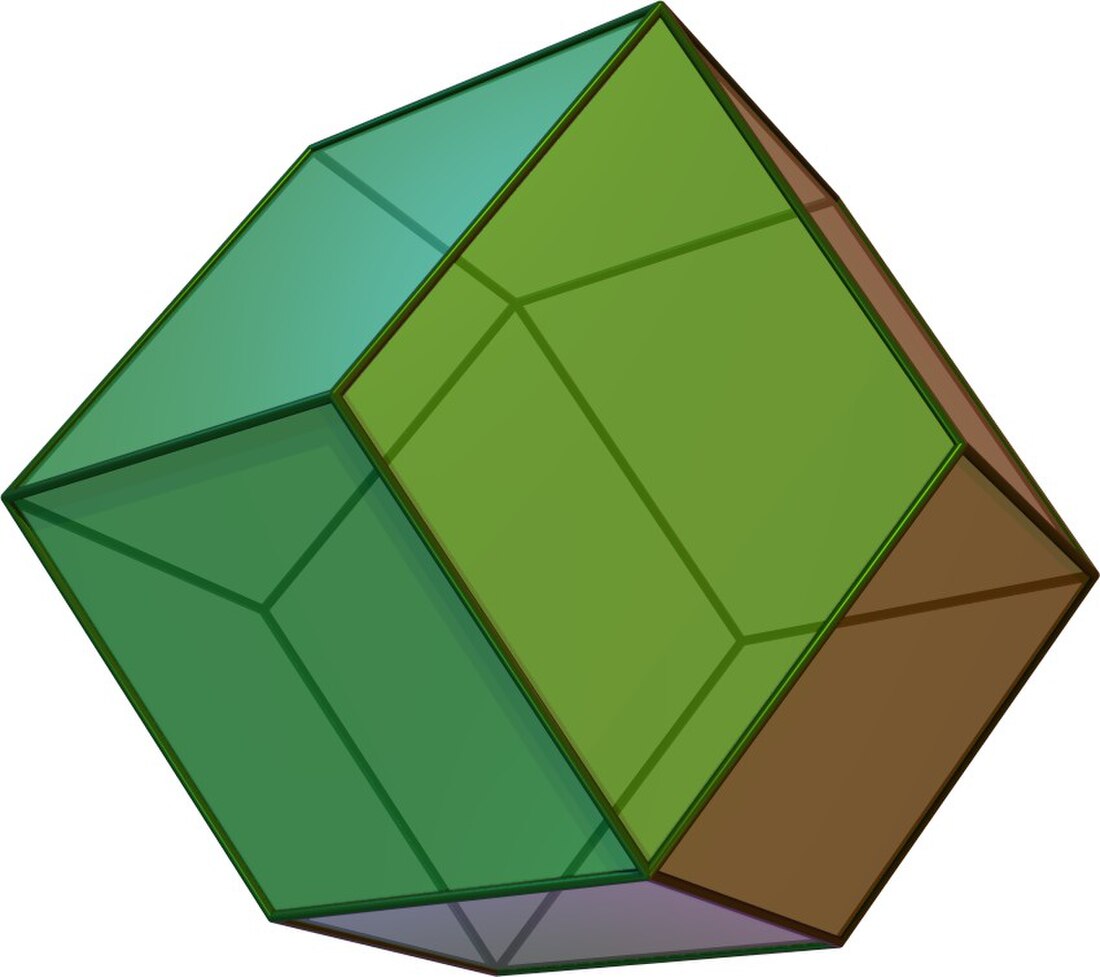
在几何学中,菱形十二面体(Rhombic dodecahedron)是一个由菱形构成的十二面体[2],由12个全等的菱形组成,具有24条边和14个顶点,其对偶多面体为截半立方体[3],是13种卡塔兰立体之一。 其具有面可递的性质,这意味著这个几何形状的对称性可在各个面上递移。菱形十二面体是一种可以独立堆砌并无空隙且不重叠地填满三维空间的立体,因此是一种空间填充多面体[4],这种堆砌结构可以对应到化学中的体心立方晶格;此外,在矿物学中,菱形十二面体也是部分矿物的晶体惯态[5]。由于菱形十二面体每个面全等,且十分均匀,因此有时会被拿来做成骰子或被设计成魔术方块。菱形十二面体有数种拓朴同构体,即几何上不同,但面的数量与每个面的边数相同、顶点间连接方式也相同的立体,例如鸢形十二面体。菱形十二面体也可以星形化。星形化后的菱形十二面体为星形菱形十二面体,当中较知名的形状是艾雪立体。


Remove ads
性质
菱形十二面体是一个卡塔兰立体,有12个面、24条边和14个顶点[1]:3,其中12面为12个全等的个菱形,且具有180度旋转对称性和点对称性,因此是一个环带多面体[6],其对偶多面体为截半立方体。
菱形十二面体能独立密铺三维空间,因此是一种空间填充多面体[4],其所形成的堆砌体称为菱形十二面体堆砌,可以视为是面心立方晶格的沃罗诺伊镶嵌。这种堆砌体是体心立方晶格(bcc)的布里元区,部分矿物可以形成于菱形十二面体的晶体惯态[5],如石榴石。蜜蜂筑巢时也是使用菱形十二面体空间填充的几何结构来筑巢,其每个蜂房皆是以半个菱形十二面体为上盖之六角柱的空间填充构成[7][8]。菱形十二面体也出现在钻石和金刚石的单位晶格中,但实际上少了4个顶点,而化学键位于剩馀的棱上[9]。
菱形十二面体可以从中心分割成4个三方偏方面体,若将菱形十二面体空间填充的每一个菱形十二面体都分割成三方偏方面体则可以形成三方偏方面体的空间填充[10][11],这意味著三方偏方面体也可以独立密铺三维空间。这种切割就好像将正六边形镶嵌的六边形切割成3个菱形而形成菱形镶嵌。
Remove ads
菱形十二面体的对偶多面体——截半立方体是一个阿基米德立体,具有点可递的性质,因此菱形十二面体具有面可递的性质,这意味著这个几何形状的对称群可在各个面上传递,换句话说,这立体上的任意两个面A和B,若透过旋转或镜射这个立体,使A移动到B原来的位置时,而两个面仍然占据了相同的空间区域[13]。
同理,菱形十二面体具有边可递的特性,这意味著,这立体上的任意两条棱A和B,透过旋转或镜射这个立体,使A移动到B原来的位置时,其棱以及其二面角仍然占据了相同的空间区域[14][15][16]。菱形十二面体是9个边可递的凸多面体之一,其他8个分别是五个柏拉图立体、截半立方体、截半二十面体和菱形三十面体。
菱形十二面体由12个全等的菱形组成,这个菱形的长对角线都是短对角线的√2倍,其中锐角的角度则为arccos(1/3)约为70.53°,钝角的角度则为 109.47°[17][1]:5,两条对角线长度与一边长的比为 [18]。
若菱形十二面体的边长为a,则其内切球半径为:[19][注 2]
外接球半径为:
Remove ads
若菱形十二面体的边长为a,则其表面积A及体积V为:[19][注 6]
若令其对偶多面体——截半立方体边长为单位长,则菱形十二面体的边长为,则其体积V为[19]:
Remove ads
 五角十二面体(Pyritohedron[20])是介于立方体和菱形十二面体之间的变体 |
 菱形十二面体的扩展 |
- (±1, ±1, ±1)
另外6个顶点为四个菱形之公共顶点,其顶点坐标为[4]:
- (±2, 0, 0), (0, ±2, 0) 和 (0, 0, ±2)
菱形十二面体可以是为五角十二面体的退化限制,其顶点坐标可表示为(±1, ±1, ±1)与(0, 1 + h, 1 − h2),其中h = 1。
正交投影
菱形十二面体有4个特殊的正交投影,分别为于四个菱形的公共顶点投影、于三个菱形的公共顶点投影、于棱上投影和于面上投影,其中“于棱上投影”以及“于面上投影”其对称性对应于B2 和 A2的考克斯特平面[21]。
其他菱形十二面体
亦有一些十二面体也是由菱形组成,例如比林斯基十二面体[22]。
菱形十二面体是一种平行多面体,具有可以独立填满三维空间的性质,其所形成的几何结构称为菱形十二面体堆砌或平行十二面体堆砌[23],其对偶可能为半立方体堆砌或由四面体和八面体组成的堆砌。
 由菱形十二面体堆砌而成的几何结构 |
 平行十二面体可由四对等长的边组成。 |
常见的由菱形组成的平行十二面体有二面体群菱形十二面体。
二面体群菱形十二面体是一种具有与一般菱形十二面体不同对称性的平行十二面体,同样可以独立填满三维空间,其所形成的几何结构类似于截角八面体堆砌的一个变种[24]。
其中一个二面体群菱形十二面体例子,例如由4个正方形和8个60度菱形所组成的平行十二面体,其具有D4h二面体群对称,且阶数为16,其外型看起来与顶面和底面摆入正四角锥的截半立方体类似。

|
 展开图 |
顶点座标
|
 依据其对称性将比林斯基十二面体之前面的面与宽边著上颜色。 |
 依照互相平行的边著色 |
比林斯基十二面体(Bilinski dodecahedron)又称为第二种菱形十二面体(菱形十二面体第2種[25][26]),是菱形十二面体的另一种基于平行十二面体的变种,由斯坦科·比林斯基于1960年发现。
比林斯基十二面体同样由12个菱形组成,但构成此几何体的菱形有两种:其中一种菱形对角线比为2个平方根,另一种菱形对角线比为黄金比例[27][28]。
使用

由于菱形十二面体每个面全等,且十分均匀,因此有时会被拿来做成骰子(但大多数都会使用正十二面体作为骰子)。亦有部分的魔术方块是设计成菱形十二面体的形状[29]。
相关多面体与镶嵌
菱形十二面体可以经由立方体透过会合变换构造,即将立方体每个面贴上角锥,并用适当的锥高,使角锥侧面与邻近面上贴的角锥之测面共面来获得。其他也是由立方体透过康威变换得到的多面体有:
菱形十二面体可以切割成截半立方体。在切割过程可以得到一些不同的多面体,例如:
菱形十二面体与小斜方截半四面体(等价于截半立方体)的对偶多面体等价,其他与正四面体相关的多面体为:
菱形十二面体可以视为由菱形组成的球面镶嵌图,一般菱形镶嵌的菱形锐角顶点是3个菱形的公共顶点,有这种性质的相关多面体与镶嵌包括:
另一种菱形镶嵌的菱形锐角顶点是4个菱形的公共顶点,而菱形十二面体也属于这类镶嵌。有这种性质的相关多面体与镶嵌包括:
此外,菱形十二面体也可以对应到面布局为V3.2n.3.2n的镶嵌图系列中。这个系列的第一种形状时平面镶嵌,其馀皆为双曲镶嵌:
 V3.4.3.4 (展开图) |
 V3.6.3.6 平面镶嵌 菱形镶嵌 |
 V3.8.3.8 双曲镶嵌 (庞加莱圆盘模型) |
部分多面体与菱形十二面体拓朴同构,例如平行十二面体,亦有一些非菱形组成的十二面体与菱形十二面体拓朴同构,例如鸢形十二面体。

鸢形十二面体[30][31][32]是一种由12个全等的鸢形组成的十二面体,具有面可递的性质,并具24阶四面体群对称性。
鸢形十二面体可以视为将菱形十二面体的菱形面变形成鸢形的结果。形变的方式是透过调整菱形十二面体的8个顶点,另外四个顶点保持正四面体的布局位置。其形变量可透过一个数组(a,b)来表示,当a和b皆为1时则为菱形十二面体,a表示保持著正四面体的布局位置的顶点,可以逐渐向1/2趋近,向1/2趋近的意义表示其顶点逐渐移向几何中心;而b的值取决于a,需要使移动时能够成平面的鸢形而非扭歪多边形,其值会向正无穷大逼近。这种情形下,其顶点坐标可以表示为:
- (±2, 0, 0), (0, ±2, 0), (0, 0, ±2)
- (a, a, a), (−a, −a, a), (−a, a, −a), (a, −a, −a)
- (−b, −b, −b), (−b, b, b), (b, −b, b), (b, b, −b)
下表列出部分数组(a,b)所形成的鸢形十二面体图像:

如同其他的凸多面体,菱形十二面体也可以透过延伸面或边,直到它们相遇形成新的多面体来进行星形化。多尔曼·露可(Dorman Luke)在他的论文中描述了一些菱形十二面体的星形化体[33]。较广为人知的是他提出的第一种多面体,其名称可以简略地称为“第一种星形菱形十二面体”。这种多面体可以视为将适当锥高的菱形锥(底面为菱形的四角锥)叠在菱形十二面体的每一个菱形面上,并且让锥高高于邻近的面来构造:
-
第一种星形菱形十二面体
-
第一种星形菱形十二面体的三维模型
对偶复合体是由一个多面体与其对偶多面体组合成的复合图形。菱形十二面体与其对偶的复合体为复合截半立方体菱形十二面体。其共有26个面、48条边和26个顶点,其尤拉示性数为4,亏格为-1[34]。
截去所有顶点后的菱形十二面体称为截角菱形十二面体。

|
| 截角菱形十二面体 |
若将菱形十二面体的六个发出四条棱的顶点截去可以获得倒角立方体[35]。

|

|
| 倒角立方体 | 倒角立方体的展开图 |
另外若将菱形十二面体的八个发出三条棱的顶点截去可以获得倒角八面体[6][36]。
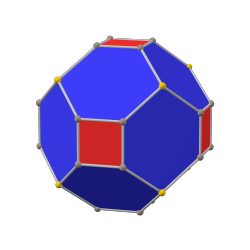 倒角立方体 |
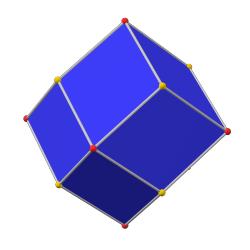 菱形十二面体 |
 倒角八面体 |
 四角化截半立方体 |
 截半立方体 |
 三角化截半立方体 |
菱形十二面体图
参见
注释
- Wolfram, Stephen. "(3/4)/(3*sqrt(6)/8)". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- Wolfram, Stephen. "(sqrt(3)/2)/(3*sqrt(6)/8)". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- Wolfram, Stephen. "(27*sqrt(2)/16)/((3*sqrt(6)/8)^3)". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
参考文献
延伸阅读
外部链接
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads