角

在几何学中，角（jiǎo）（英语：angle）或精确用语平面角，是由两条有公共端点的射线组成的几何对象。这两条射线叫做角的边，它们的公共端点叫做角的顶点。一般的角会假设在欧几里得平面上，但在非欧几里得几何中也可以定义角，特别是在球面几何学中的球面角（英语：spherical angle）是用大圆的圆弧代替射线。角在几何学和三角学中有着广泛的应用。

此条目的主题是数学名词角。关于与“角”标题相近或相同的条目，请见“角 (消歧义)”。

Unicode中的角符号，码位为U+2220

几何之父欧几里得曾定义角为在平面中两条不平行的直线的相对斜度。普罗克鲁斯认为角可能是一种特质、一种可量化的量、或是一种关系。欧德谟（英语：Eudemus）认为角是相对一直线的偏差，安提阿的卡布斯（英语：Carpus of Antioch）认为角是二条相交直线之间的空间。欧几里得认为角是一种关系，不过他对直角、锐角或钝角的定义都是量化的^[1]。

平面角大小的计量单位制常用的有360度制、弧度制等^[2][3]。

表示方法

角通常用三个字母表示：两条边上的点的字母写在两旁，顶点上的字母写在中间。图中的角用∠AOB或${\displaystyle {\widehat {AOB}}}$表示。但若在不会产生混淆的情形下，也会直接用顶点的字母表示，例如角∠O。

在数学式中，一般会用希腊字母（${\displaystyle \alpha ,\beta ,\gamma ,\theta ,\varphi ,...}$）表示角的大小。为避免混淆，符号π一般不用来表示角度。

角的测量

常见测量单位

以角的端点为圆心做圆弧。由于圆弧的半径和弧长成正比，而角是长度的比例，所以圆的大小不会影响角的测量。

• 角度：由角在圆上所切出的圆弧的长度除以圆的周长再乘以360的结果，一般用°来标记，读作“度”。一度可以继续分为60“分”或3600“秒”。角度在天文学和全球定位系统中有重要应用。

• 弧度：用角在圆上所切出的圆弧的长度除以圆的半径，单位是rad（中文名：弪）。弧度在数学中有广泛的应用。弧度还是国际单位制中规定的角的标准度量，但却不是中国法定计量单位，角度则是角在中国的法定计量单位。

采用弧度时，通常不会标示单位，例如：${\displaystyle \sin \pi =\sin 180^{\circ }=0}$

• 百分度：是角在圆上所切出的圆弧的长度除以圆的周长再乘以400的结果。

其他测量单位

角度的量测可以视为弧长s和半径r的比例，再依选用单位乘以一比例系数${\displaystyle {\frac {2\pi }{n}}}$。

${\displaystyle \theta ={\frac {n}{2\pi }}{\frac {s}{r}}}$

例如以上的弧度、角度和百分度，其转换系数${\displaystyle n}$分别为${\displaystyle 2\pi }$、360和400。

以下是一些其他的测量单位，对应不同的${\displaystyle n}$值。

• 圈数或转数（${\displaystyle n=1}$）：是指完整旋转一圈，依应用的不同，会简写为cyc、rev或rot，不过在每分钟转速（RPM）的单位中，只用一个字母r表示。
• 直角（${\displaystyle n=4}$）：是${\displaystyle {\frac {1}{4}}}$圈，是几何原本中用的角度单位，直角${\displaystyle =90^{\circ }={\frac {\pi }{2}}\mathrm {rad} ={\frac {1}{4}}\mathrm {turn} =100\mathrm {grad} }$。在德文中曾用${\displaystyle \llcorner }$表示直角。
• 时角（${\displaystyle n=24}$）：）常用在天文学中，是${\displaystyle {\frac {1}{24}}}$圈。此系统是用在一天一个周期的循环（例如星星的相对位置），其六十进制下的子单位称为“时间分角”及“时间秒角”，这两个单位和角度的角分及角秒不同，前者大小为后者的十五倍。1时角${\displaystyle =15^{\circ }={\frac {\pi }{12}}\mathrm {rad} ={\frac {1}{6}}\mathrm {quad} ={\frac {1}{24}}\mathrm {turn} \approx 16.667\mathrm {grad} }$。
• 密位（${\displaystyle n=6000\sim 6400}$）：此单位是指一个单位大约等于毫弧度的角度，有许多不同的定义，其数值从0.05625度到0.06度（3.375至3.6角分），而毫弧度约为0.05729578度（3.43775角分）。在北大西洋公约组织的国家中，密位定义为圆的${\displaystyle {\frac {1}{6400}}}$。其数值大约等于一个角度的弧长为一公尺，其半径为一公里的角度（${\displaystyle {\frac {2\pi }{6400}}=0.0009817...\doteqdot {\frac {1}{1000}}}$）。瑞典历史上以圆周为6300密位（最接近），但在2007年同北约一致。
• 角分（${\displaystyle n=21600}$）：定义为一度的${\displaystyle {\frac {1}{60}}}$，是${\displaystyle {\frac {1}{21600}}}$圈，会用 ′ 表示，例如3° 30′ 等于${\displaystyle 3+{\frac {30}{60}}}$度，也就是3.5度，有时也会出现小数，例如${\displaystyle 3^{\circ }5.72'=3+{\frac {5.72}{60}}}$度。海里曾定义为在地球的大圆上一角分的弧长。
• 角秒 （${\displaystyle n=1296000}$）：定义为一角分的${\displaystyle {\frac {1}{60}}}$，会用 ″ 表示，例如3° 7′ 30″等于${\displaystyle 3+{\frac {7}{60}}+{\frac {30}{3600}}}$度，或是3.125 度。

正角和负角

以上角的定义均未考虑数值为负的角。不过在一些应用时，会将角的数值加上正负号，以标明是相对参考物不同方向的旋转。

在二维的笛卡儿坐标系中，角一般是以x轴的正向为基准，若往y轴的正向旋转，则其角为正角，若往y轴的负向旋转，则其角为负角。若二维的笛卡儿坐标系也是x轴朝右，y轴朝上，则逆时针的旋转对应正角，顺时针的旋转对应负角。

一般而言，${\displaystyle -\theta }$角和一圈减去${\displaystyle \theta }$所得的角等效。例如${\displaystyle -45^{\circ }}$和${\displaystyle 360^{\circ }-45^{\circ }(=315^{\circ })}$等效，但这只适用在用角表示相对位置，不是旋转概念时。旋转${\displaystyle -45^{\circ }}$和旋转315°是不同的。

在三维的几何中，顺时针及逆时针没有绝对的定义，因此定义正角及负角时均需列出其参考的基准，一般会以一个通过角的顶点，和角所在平面垂直的向量为基准。

在导航时，导向是以北方为基准，正向表示顺时针，因此导向45°对应东北方。导向没有负值，西北方对应的导向为315°。

其他量测角大小的方法

除了量测角本身的大小外．也有其他的方式，可以量测角的大小。

坡度等于一个角的正切值，常用百分比或千分比来表示。当一个角的坡度小于5%时，其坡度近似于角以弧度表示的数值。

在有理几何学（英语：rational geometry）中，一个角的大小是以伸展度（spread）来表示，伸展度定义为角对应正弦的平方，而任一角正弦的平方和该角补角正弦的平方相等。因此任一角和其补角在有理几何学中是等同的。

角的种类

个别的角

零角

角度等于0°，或弧度为0的角。

锐角

角度大于0°且小于90°，或弧度大于0且小于${\displaystyle {\frac {\pi }{2}}}$的角。

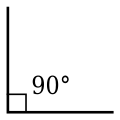
直角

角度等于90°，或弧度为${\displaystyle {\frac {\pi }{2}}}$的角。

钝角

角度大于90°且小于180°，或弧度大于${\displaystyle {\frac {\pi }{2}}}$且小于${\displaystyle \pi }$的角。

平角

角度等于180°，或弧度为${\displaystyle \pi }$的角。

优角或反角

角度大于180°且小于360°，或弧度大于${\displaystyle \pi }$且小于${\displaystyle 2\pi }$的角。

周角

角度等于360°，或弧度为${\displaystyle 2\pi }$的角。

• 
  直角
• 
  优角（或作反角）
• 
  周角
• 
  锐角（a）、钝角（b）和平角（c）

以下是各角度的名称及不同单位下的数值：

名称	零角	锐角	直角	钝角	平角	优角	周角
单位	范围
转	${\displaystyle 0}$	${\displaystyle (0,{\tfrac {1}{4}})}$	${\displaystyle {\tfrac {1}{4}}}$	${\displaystyle ({\tfrac {1}{4}},{\tfrac {1}{2}})}$	${\displaystyle {\tfrac {1}{2}}}$	${\displaystyle ({\tfrac {1}{2}},1)}$	${\displaystyle 1}$
弧度	${\displaystyle 0\pi \,}$	${\displaystyle (0,{\tfrac {1}{2}}\pi )}$	${\displaystyle {\tfrac {1}{2}}\pi }$	${\displaystyle ({\tfrac {1}{2}}\pi ,\pi )}$	${\displaystyle \pi }$	${\displaystyle (\pi ,2\pi )}$	${\displaystyle 2\pi \,}$
度	${\displaystyle 0^{\circ }}$	${\displaystyle (0^{\circ },90^{\circ })}$	${\displaystyle 90^{\circ }}$	${\displaystyle (90^{\circ },180^{\circ })}$	${\displaystyle 180^{\circ }}$	${\displaystyle (180^{\circ },360^{\circ })}$	${\displaystyle 360^{\circ }}$

令x为该角度数。

角的组合

有三种特殊角的组合，其度数和均为特殊的值：

• 馀角：当两个角的度数之和等于90°，即一个直角，这两个角便是馀角。若两个相邻的角互为馀角，两个非共用边会形成直角。在欧几里得几何中，非直角的两角即互为馀角。

若角A和B互为馀角，以下的数学式会成立：

${\displaystyle {\begin{aligned}\sin ^{2}A+\sin ^{2}B&=1\\\cos ^{2}A+\cos ^{2}B&=1\\\tan A&=\cot B\\\sec A&=\csc B\end{aligned}}.}$

（一角的正切等于其馀角的馀切，一角的正割等于其馀角的馀割）

三角函数中的馀函数，其前缀“co-”就是馀角的意思。

• 补角：当两个角的度数之和等于180°，即一个平角，这两个角便是互补角。若两个相邻的角互为馀角，两个非共用边会形成一直线。不过两个不相邻的角也可以是补角，例如平行四边形中，任两邻角为互补角。圆内接四边形的对角也是互补角。

若点P为圆O外的一点，而过点P作圆的切线，切点分别在点T和点Q，则∠TPQ和∠TOQ为互补角。

两互补角的正弦相等，其馀弦及正切（若有定义义）大小相等，但符号异号。

在欧几里得几何中，三角形两角的和为第三角的补角。

• explementary angles or conjugate angles. 当两个角的度数之和等于360°

互为馀角的角a和角b

图中的锐角和钝角形成一组互补角

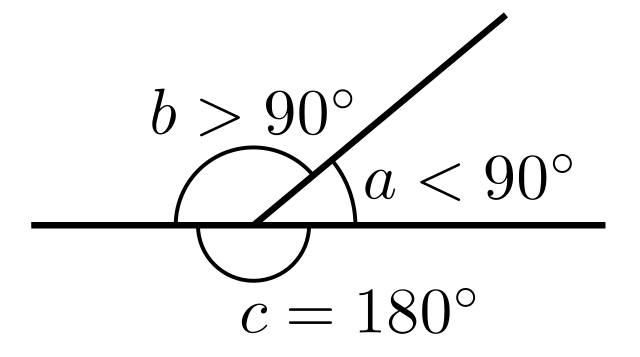
常用定理

同顶角

同顶角

${\displaystyle a+b+c=360^{\circ }}$

直线上的邻角

直线上的邻角

${\displaystyle a+b+c=180^{\circ }}$

与平行线有关的定理

与平行线有关的定理

当${\displaystyle AE}$平行于${\displaystyle BD}$,

• ${\displaystyle a=c}$（同位角，${\displaystyle AE//BD}$）
• ${\displaystyle b=d}$（内错角，${\displaystyle AE//BD}$）
• ${\displaystyle b+c=180^{\circ }}$（同旁内角，${\displaystyle AE//BD}$）

由角度的关系也可以推得两直线平行

• 当${\displaystyle a=c}$，${\displaystyle AE}$平行于${\displaystyle BD}$（同位角相等）
• 当${\displaystyle b=d}$，${\displaystyle AE}$平行于${\displaystyle BD}$（内错角相等）
• 当${\displaystyle b+c=180^{\circ }}$，${\displaystyle AE}$平行于${\displaystyle BD}$（同旁内角互补）

二曲线的夹角

二曲线在P点的夹角定义为二曲线在P点切线A和B的夹角

曲线和直线的夹角或是二曲线间的夹角定义为二曲线在交点处切线的夹角。

点积及其拓展

在欧几里得空间中，二个向量u及v的角和其点积及向量的长度有关：

${\displaystyle \mathbf {u} \cdot \mathbf {v} =\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}$

依上式可以用二个平面（或曲面）的法向量，计算二者之间的夹角，也可以根据二歪斜线的向量计算其夹角。

内积

在一个抽象的实数内积空间中，在定义角时可以用内积 ${\displaystyle \langle \cdot ,\cdot \rangle }$取代欧几里得空间的点积( · )：

${\displaystyle \langle \mathbf {u} ,\mathbf {v} \rangle =\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}$

在复数的内积空间中，为了使馀弦的数值仍维持实数，因此需修改为

${\displaystyle \operatorname {Re} (\langle \mathbf {u} ,\mathbf {v} \rangle )=\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}$

或者使用绝对值的标示：

${\displaystyle |\langle \mathbf {u} ,\mathbf {v} \rangle |=\cos(\theta )\ \|\mathbf {u} \|\ \|\mathbf {v} \|.}$

后者不考虑向量的方向，因此是描述由向量${\displaystyle \mathbf {u} }$及${\displaystyle \mathbf {v} }$所生成的二个一维子空间${\displaystyle \operatorname {span} (\mathbf {u} )}$及${\displaystyle \operatorname {span} (\mathbf {v} )}$之间的夹角。

黎曼几何中的角

在黎曼几何中，利用度量张量来定义二条切线之间的夹角，其中U及V是切线向量，g_ij 是度量张量G的分量。

${\displaystyle \cos \theta ={\frac {g_{ij}U^{i}V^{j}}{\sqrt {\left|g_{ij}U^{i}U^{j}\right|\left|g_{ij}V^{i}V^{j}\right|}}}.}$

地理学及天文学中的角

以地理的观点，地球上任何一个位置都可以用地理座标系统来表示，此系统标示位置的经度及纬度，两者都以此点连至地球球心连线的角度来表示，经度是以格林威治子午线为参考基准，而纬度是以赤道为参考基准。

在天文学中，天球的一点可以用任何一种天球坐标系统来表示，不过其基准则因坐标系统不同而不同。天文学量测二颗星星的角距离时，会假想分别有二颗星星分别和地球连成的直线，再量测这二条直线的夹角，即为角距离。

天文学家也会用角直径量测一物体的表观大小。例如满月的角直径约为0.5°。小角公式可以将上述的角测量转换为距离和大小的比值。

相关条目

• 角平分线
• 辐角
• 圆心角
• 余角
• 大圆距离
• 量角器
• 立体角
• 补角
• 无理角（英语：Irrational rotation）
• 角速度

参考资料

1. Heiberg, Johan Ludvig. Heath, T. L. , 编. Euclid. The thirteen books of Euclid's Elements 1. Cambridge University press. 1908: 177–178 [2012-08-24]. （原始内容存档于2011-07-30）.
2. https://terms.naer.edu.tw/detail/b079b1a2250d7cff36338922ce22c5cd/
3. GB 3102.1-1993：空间和时间的量和单位（代替GB 3102.1-1986）．1993年12月27日公布，1994年7月1日实施．

外部链接

• 《中华人民共和国法定计量单位 （页面存档备份，存于互联网档案馆）》