扭棱立方体
来自维基百科,自由的百科全书
在几何学中,扭棱立方体(英语:snub cube[1]),又称拟立方体(英语:cubus simus[2][3])是一种由38个面组成的阿基米德立体[4],由6个正方形和32个正三角形组成,共有60条边和24个顶点[5]。

性质
扭棱立方体是一个手性多面体[6],也就是说,该多面体镜射之后会跟原本的型形状不同,无法借由旋转半周再回到原本的形状[7][8][9]。扭棱立方体是一种阿基米德立体,其所有的面都是正多边形,且每个顶点都是4个三角形和一个正方形,其顶点图计为3.3.3.3.4或34.4[10],由于所有顶点相等,因此也称为半正多面体。
其中t表示三波那契常数:
- 。
扭棱立方体有两种不同角度的二面角,分别是三角形-三角形二面角和三角形-正方形二面角。其中三角形-三角形二面角馀角的馀弦值是三次方程的零点、三角形-正方形二面角馀角的馀弦值是六次方程的零点。
三角形-三角形二面角以反正割表示为:
换算成角度约为153.23度或153度14分04秒。
三角形-正方形二面角为:
换算成角度约为142.98度或142度59分00秒。
正交投影
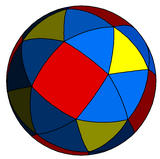
球面镶嵌
几何关联

扭棱立方体可透过将立方体的正方形面向外拉,使之不再相连,然后再将正方形面旋转一个角度,再将空隙以三角形补满而得
 扭棱立方体 |
 立方体 |
 小斜方截半立方体 |
 扭棱立方体 |
相关多面体及镶嵌
扭棱立方体是立方体经过扭棱变换后的结果,其他也是由立方体透过康威变换得到的多面体有:
参见
参考文献
外部链接
Wikiwand - on
Seamless Wikipedia browsing. On steroids.







![{\displaystyle {\tfrac {1+{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}}{3}}\approx 1.839\,29}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6384a79e4dc2dc59d706d9662df1968f38208de7)