Дванадцятигранник

Дванадцятигранник або додекаедр (дав.-гр. δωδεκάεδρον (dōdekáedron) ; від грец. δώδεκα (dṓdeka) — дванадцять і грец. ἕδρα (hédra) — грань) — довільний многогранник із дванадцятьма гранями.

Деякі найбільш відомі додекаедри

Ih[en], порядок 120
Правильний додекаедр	Малий зірчастий додекаедр	Великий додекаедр	Великий зірчастий додекаедр
Th, порядок 24	T, порядок 12	Oh[en], порядок 48	Многогранник Джонсона (J84)
Піритоедр	Тетартоїд	Ромбододекаедр	Кирпатий двоклиноїд[en]
D4h[en], порядок 16		D3h[en], порядок 12
Ромбо-шестикутний додекаедр[en]	Ромбо-квадратний додекаедр	Ромбо-трапецоїдний додекаедр[en]	Ромбо-трикутний додекаедр

Існує 6 384 634 топологічно різних опуклих додекаедрів, не враховуючи тих, що отримані шляхом дзеркального відбиття, з кількістю вершин від 8 до 20.^[1]

(Два многогранники вважають "топологічно різними", якщо вони мають різну структуру розташування граней і вершин, так що неможливо перетворити один в інший, просто змінивши довжини ребер або кути між ребрами чи гранями).

Правильний додекаедр

Найбільш відомий додекаедр — це правильний додекаедр, всі грані якого є правильними п'ятикутниками. Він є найбільш симетричним з усіх опуклих додекаедрів, має ікосаедричну симетрію^[en] I_h, порядок 120.

Деякі додекаедри мають таку ж комбінаторну структуру, як і правильний додекаедр (в сенсі графа, утвореного його вершинами і ребрами), але їх п'ятикутні грані не є правильними:

— піритоедр, поширена кристалічна форма піриту, має піритоедричну симетрію T_h,

— тетартоїд має хіральну тетраедричну симетрію T.

Ромбододекаедр

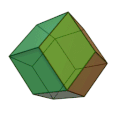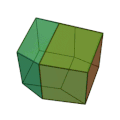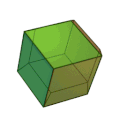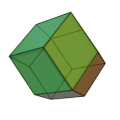
Ромбододекаедр можна розглядати як граничний випадок піритоедра, і він має октаедричну симетрію^[en] O_h. Ромбододекаедр є паралелоедром^[en], зоноедром а також двоїстим до кубооктаедра (напівправильного многогранника Архімеда).

Ромбо-шестикутний додекаедр^[en] (або подовжений додекаедр, або гексоромбододекаедр), ромбо-трапецоїдний додекаедр^[en] а також ромбододекаедр можуть утворювати стільники, що замощують тривимірний простір без проміжків та накладень.

Правильний додекаедр

Докладніше: Правильний додекаедр

Опуклий правильний додекаедр є одним з п'яти правильних многогранників Платона і може бути представлений своїм символом Шлефлі як {5, 3}, тобто кожна вершина оточена трьома правильними п'ятикутними гранями.

Двоїстим многогранником до правильного додекаедра є правильний ікосаедр {3, 5}, кожна вершина якого оточена п'ятьма правильними трикутними гранями.

Опуклий правильний додекаедр має три зірчасті форми; всі три є правильними зірчастими многогранниками Кеплера — Пуансо. Їх гранями є правильні п'ятикутники та правильні пентаграми.

Зірчасті форми правильного додекаедра

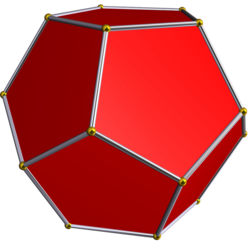Опуклий правильний додекаедр

Малий зірчастий додекаедр {5/2, 5}

Великий додекаедр {5, 5/2}

Великий зірчастий додекаедр {5/2, 3}

Характерною особливістю правильного додекаедра (також і правильного ікосаедра) є наявність в нього осей обертової симетрії 5-го порядку, які не дозволені правилами кристалографії ^{[2]:Стор.41} , тобто в природі не існує кристалів мінералів, що мають форму правильного додекаедра. Проте можна зустріти квазікристали у формі правильного додекаедра (наприклад, квазікристал гольмій — магній — цинку (Ho-Mg-Zn)). Також існують мінерали, що мають форму додекаедра з неправильними гранями (наприклад, пірит).

Додекаедри з п'ятикутними гранями

В кристалографії в деяких класах симетрії кубічної кристалічної системи можуть траплятися два основних види додекаедрів, які топологічно еквівалентні правильному додекаедру, але мають менший порядок симетрії (тобто менш симетричні): піритоедр з піритоедричною симетрією і тетартоїд з хіральною тетраедричною симетрією:

Піритоедр

Піритоедр
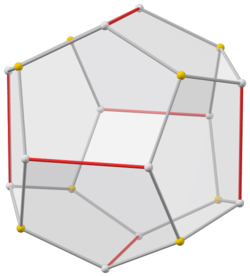Натисніть тут , щоб подивитися обертання моделі
Властивості	Опуклий, гране-транзитивний
Комбінаторика
Елементи	12 п'ятикутних граней 30 ребер (6 + 24) 20 вершин (8 + 12) (3-го степеня)
Грані	12 Рівнобедрених п'ятикутників
Характеристика Ейлера	${\displaystyle \chi =\Gamma -{\hbox{P}}+{\hbox{B}}=2}$
Класифікація
Діаграма Коксетера-Динкіна	(або o4p3p )
Група симетрії	Th,[4,3+], (3*2), порядок 24 (Піритоедрична симетрія)
Група обертань	T, [3,3]+, (332), порядок 12
Двоїстий многогранник	Ікосаедр з піритоедричною симетрією
Розгортка

Піритоедр ^{[3] [4] [5]} (або пентагондодекаедр ^{[6]:Стор.80-81 [7]:Стор.136} ,) — це додекаедр з піритоедричною симетрією (T_h). Має 12 конгруентних п'ятикутних дзеркально-симетричних граней (тобто симетричних відносно осі, що проходить через вершину і середину протилежної сторони).

Має 20 вершин, розділених на два типи; в кожній вершині сходяться три грані.

Його 30 ребер також розділені на два типи — 24 і 6 ребер однакової довжини.

Єдиними осями обертової симетрії є три взаємно перпендикулярні осі 2-го порядку та чотири осі 3-го порядку. Осі симетрії п'ятого порядку відсутні, що дозволяє цьому многограннику бути формою для кристалів. Зокрема, форму піритоедру має кристал мінералу піриту.

Кристал піриту

Кристал піриту найчастіше зустрічається у двох поширених кристалічних формах — піритоедр та куб. У піриту, що має форму піритоедру, грані мають індекс Міллера {2,1,0}, що означає, що двогранний кут становить 2·arctan(2) ≈ 126.87°, а кути кожної п'ятикутної грані становлять: кут ≈ 121,6° розташований між двома кутами ≈ 106,6° і навпроти двох кутів ≈ 102,6°. Наступні формули описують розміри граней ідеального кристала (який рідко зустрічається в природі).

${\displaystyle {\text{Висота}}={\frac {\sqrt {5}}{2}}\cdot L}$

${\displaystyle {\text{Ширина}}={\frac {4}{3}}\cdot L}$

${\displaystyle l={\sqrt {\frac {7}{12}}}\cdot L}$

де ${\displaystyle l}$ — довжина короткого ребра многогранника; ${\displaystyle L}$ — довжина довгого ребра.

Природний пірит (На правому зображенні показано кути грані)

Декартові координати вершин

Вісім вершин, що формують вершини куба, вписаного в многогранник, мають координати: (±1, ±1, ±1). При цьому довжина ребер куба дорівнює 2.

Координати інших дванадцяти вершин:

(0, ±(1 + h), ±(1 − h²)), (±(1 + h), ±(1 − h²), 0) та (±(1 − h²), 0, ±(1 + h)).

де h — висота клиноподібного "даху" над гранями куба.

При h = 0 отримаємо вироджений піритоедр, що має форму куба, але з додатковими вершинами та ребрами на його гранях.

При h = 1/2 (чверть довжини ребра куба), отримаємо «бездоганний» (з геометричної точки зору) кристал природного піриту.Також в цьому випадку многогранник є піритоедром у моделі Вейра — Фелана^[en].

При h = 1/φ = √5 − 1/2= 0.618..., отримаємо правильний додекаедр.

При h = 1 отримаємо вироджений піритоедр, у якого деякі вершини збігаються, а ребра між ними зменшуються до нульової довжини; він приймає форму ромбдодекаедра.

Ортографічні проєкції піритоедру з висотою h = 1/2

Піритоедри з висотою h = 1/2 та h = 1/φ

Геометричні варіації

Піритоедр має деякий ступінь свободи у геометричній будові; при цьому на одній межі маємо куб, коли певні ребра стають колінеарними одне до одного, а на іншій межі маємо ромбододекаедр, коли 6 ребер вироджуються до нульової довжини. Правильний додекаедр являє собою особливий проміжний випадок, коли всі ребра і кути рівні.

Можна перетнути ці граничні випадки, та отримати при цьому неопуклі піритоедри.

Перетнувши нижню межу опуклого піритоедру, що має вигляд куба, отримаємо неопуклі його форми; неопуклий піритоедр з рівними сторонами (ендо-додекаедр) в поєднанні з опуклим правильним додекаедром може утворювати стільники, що замощують тривимірний простір без проміжків та накладень.

Продовжуючи деформацію многогранника у цьому напрямку, ми проходимо через вироджений випадок, коли дванадцять вершин збігаються в центрі, і переходимо до правильного великого зірчастого додекаедра, в якого всі ребра і кути знову рівні, а грані приймають форму правильних пентаграм.

Перетнувши верхню межу опуклого піритоедру, що має вигляд ромбододекаедра, отримаємо неопуклий рівносторонній додекаедр з рибоподібними рівносторонніми п'ятикутними гранями з самоперетином.

Анімації
Стільники з чергуванням опуклих і увігнутих піритоедів з висотами h в межах ±1/φ	Піритоедри з висотами між h = 0 (куб) та h = 1 (ромбододекаедр)

• 
  Індекс грані {10,9,0}
• 
  Індекс грані {2,1,0}
• 
  Індекс грані {7,1,0}

Окремі випадки піритоедрів
Версії з висотами, що рівні по модулю але з протилежними знаками спільно утворюють стільники. (Див. анімацію). Показано співвідношення довжин ребер, а саме тих, що належать до набору з 24 ребер (що перетинаються в вершинах куба) до тих, що належать до набору з 6 ребер (відповідають граням куба).
Відношення	1 : 1	0 : 1	1 : 1	2 : 1	1 : 1	0 : 1	1 : 1
h	−√5 + 1/2	−1	−√5 + 1/2	0	√5 − 1/2	1	√5 + 1/2
	−1.618...		−0.618...		0.618...		1.618...
Зображення	Великий зірчастий додекаедр, грані якого є правильними пентаграмами	Вироджений випадок з 12-ма вершинами многогранника в його центрі	Неопуклий рівносторонній піритоедр (додекаедр).	Куб з додатковими вершинами та ребрами на його ребрах та гранях відповідно (як показано на рисунку) є граничним випадком опуклого піритоедра.	Правильний додекаедр є проміжним випадком з рівними ребрами та кутами.	Ромбододекаедр є граничним випадком опуклого піритоедра, коли 6 його ребер зменшуються до нульової довжини.	Рівносторонній додекаедр з гранями, що мають самоперетин.

Тетартоїд

Тетартоїд Тетрагональний п'ятикутний додекаедр
Натисніть тут, щоб подивитися обертання моделі
Властивості	Опуклий, гране-транзитивний
Комбінаторика
Елементи	12 п'ятикутних граней 30 ребер (6+12+12) 20 вершин (4+4+12) (3-го степеня)
Грані	12 п'ятикутників
Характеристика Ейлера	${\displaystyle \chi =\Gamma -{\hbox{P}}+{\hbox{B}}=2}$
Класифікація
Позначення	gT (в нотації Конвея[en] )
Діаграма Коксетера-Динкіна	(або p3p3p )
Група симетрії	T,[3,3]+, (332), порядок 12 (Хіральна тетраедрична симетрія)
Двоїстий многогранник	Ікосаедр з тетраедричною симетрією (або кирпатий тетраедр)

Тетартоїд (також тетрагональний п'ятикутний додекаедр ^{[7]:Стор.140-141; 144} , пентагонтритетраедр ^{[6]:Стор.79} і тетраедричний пентагондодекаедр) — це додекаедр з хіральною тетраедричною симетрією (Т).

Має 12 конгруентних п'ятикутних граней.

Має 20 вершин, розділених на три типи; в кожній вершині сходяться три грані.

Його 30 ребер також розділені на три типи — 12, 12 і 6 ребер однакової довжини.

Осі обертової симетрії 5-го порядку відсутні, що дозволяє цьому многограннику бути формою для кристалів.

Назва тетартоїд має грецьке коріння, та означає "четверта частина", оскільки він має одну четверту від повної октаедричної симетрії^[en] і половину піритоедричної симетрії. ^[8]

Таку форму симетрії (пентагон-тритетраедричну) може мати мінерал кобальтин.^[9]

Тетартоїд має два вироджених граничних випадки, які топологічно еквівалентні самому многограннику та мають його симетрію. Вони являють собою з одного боку — куб з додатковими ребрами на гранях (але не колінеарними до його ребер) та додатковими вершинами на ребрах куба; з іншого боку — тетраедр, кожне ребро якого поділено на три частини і кожна з двох нових вершин з'єднується з центром грані. (В нотації многогранників Конвея^[en] це є скручений тетраедр).

Ортографічні проєкції , центровані по осям симетрії 2-го та 3-го порядку

Вироджені форми тетартоїда — кубічна та тетраедрична

Мінерал кобальтин

Зв'язок з диакіс-додекаедром[en]

Тетартоїд можна утворити, збільшивши розміри 12 з 24 граней диакіс додекаедра. [7]:Стор.137 , (Зображений тут тетартоїд отримано шляхом збільшення розмірів 24 з 48 граней гекзакісоктаедра[en] (або дисдакіс додекаедра)). Хіральні тетартоїди, базовою основою яких є диакіс додекаедр. Модель кристалу Модель кристалу праворуч являє собою тетартоїд, утворений шляхом збільшення синіх граней ядра дисдакіс додекаедра. Тому ребра між синіми гранями покрито червоними каркасними ребрами.

Декартові координати вершин

Наступні точки є вершинами п'ятикутника тетартоїда з тетраедричною симетрією:

(a, b, c); (−a, −b, c); (−n/d₁, −n/d₁, n/d₁); (−c, −a, b); (−n/d₂, n/d₂, n/d₂),

при наступних умовах:^[10]

0 ≤ a ≤ b ≤ c,

n = a²c − bc²,

d₁ = a² − ab + b² + ac − 2bc,

d₂ = a² + ab + b² − ac − 2bc,

nd₁d₂ ≠ 0.

Геометричні варіації

Правильний додекаедр є тетартоїдом, всі грані якого правильні п'ятикутники, тобто він має більш розширену симетрію, ніж необхідно для тетартоїда.

Триакіс тетраедр є виродженим тетартоїдом, у якого 12 ребер зменшені до нульової довжини. (На рисунку основної таблиці вище: білі вершини і зелені ребра поглинуться зеленими вершинами.)

Варіації тетартоїда від правильного додекаедра до триакіс тетраедра

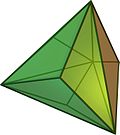Двоїстий многогранник до скрученого трисхилого біантикупола

Ще одним прикладом додекаедра з п'ятиткутними гранями є двоїстий многогранник до трисхилого повернутого біантикупола, тобто многогранника, що отриманий шляхом з'єднання двох трисхилих антикуполів основами в повернутій орієнтації.

Цей многогранник має D_3d^[en] симетрію, порядку 12. Його грані — дві групи з трьох конгруентних п'ятикутних граней розділені поясом з 6-ти конгруентних п'ятикутних граней, які поєднані між собою з чергуванням орієнтації.

Ромбододекаедр

Докладніше: Ромбододекаедр

Ромбододекаедр

Ромбододекаедр — це додекаедр, що має дванадцять ромбічних граней та володіє октаедричною симетрією^[en]. Він є зоноедром, а також двоїстим до квазіправильного кубооктаедра (архімедового тіла); зустрічається в природі у вигляді кристалів. Ромбододекаедр утворює стільники, що заповнюють тривимірний простір без проміжків та накладень.

Ромбододекаедр можна розглядати як вироджений піритоедр, у якого 6 певних ребер зменшені до нуля, а отже, п'ятикутники перетворюються на ромбічні грані.

Ромбододекаедр має кілька зірчастих форм, перша^[en] з яких також утворює стільник для замощення простору.

Інший важливий ромбододекаедр — додекаедр Білінського^[en], має дванадцять граней, що конгруенті граням ромботриаконтаедра, тобто діагоналі знаходяться у співвідношенні золотого перетину. Він також є зоноедром і був описаний Білінським у 1960 році. ^[11] Цим многогранником можна замостити простір без проміжків та накладень, а також він може зустрічатися в неперіодичних стільниках разом з ромботриаконтаедром, ромбоікосаедром^[en] і ромбогексаедром.^[12]

Деякі інші додекаедри

Як було зазначено вище, існує 6 384 634 топологічно різних опуклих додекаедрів, не враховуючи тих, що отримані шляхом дзеркального відбиття, з кількістю вершин від 8 до 20.^[1]

Деякі топологічно різні додекаедри (за винятком додекаедрів з п'ятикутними та ромбічними гранями):

• Однорідні многогранники:
  • Десятикутна призма — грані: 10 квадратів, 2 правильних десятикутників; симетрія: D_10h^[en], порядок 40.
  • П'ятикутна антипризма — грані: 10 правильних трикутників, 2 правильних п'ятикутників; симетрія: D_5d^[en], порядок 20
• Многогранники Джонсона (правильногранні):
  • П'ятисхилий купол^[en] — грані: 5 правильних трикутників, 5 квадратів, 1 правильний п'ятикутник, 1 правильний десятикутник; симетрія: C_5v^[en], порядок 10
  • Кирпатий двоклиноїд — грані: 12 правильних трикутників, симетрія: D_2d^[en], порядок 8
  • Подовжена чотирикутна біпіраміда^[en] — грані: 8 правильних трикутників та 4 квадратів; симетрія: D_4h^[en], порядок 16
  • Двічі косо відсічений ікосаедр^[en] — грані: 10 правильних трикутників та 2 правильних п'ятикутників; симетрія: C_2v^[en], порядок 4
• З конгруентними неправильними гранями: (гране-транзитивні)
  • Шестикутна біпіраміда^[en] — грані: 12 рівнобедрених трикутників; симетрія: D_6h^[en], порядок 24 — двоїстий до шестикутної призми.
  • Шестикутний трапецоедр^[en] — грані: 12 дельтоїдів; симетрія: D_6d^[en], порядок 24 — двоїстий до шестикутної антипризми.
  • Триакіс тетраедр — грані:12 рівнобедрених трикутників; симетрія: T_d , порядок 24 — двоїстий до зрізаного тетраедра (многогранника Архімеда).
• Інші додекаедри з меншою кількістю правильних граней:
  • Одинадцятикутна піраміда — грані: 11 рівнобедрених трикутників та 1 правильний одинадцятикутник; симетрія: C_11v^[en], порядок 11
  • Ромбо-трапецоїдний додекаедр^[en] — грані: 6 ромбів, 6 трапецій; симетрія: D_3h^[en], порядок 12 — двоїстий до трисхилого прямого бікупола (многогранника Джонсона J₂₇).
  • Ромбо-шестикутний додекаедр^[en] або подовжений додекаедр — грані: 8 ромбів та 4 правильних шестикутників; симетрія: D_4h^[en], порядок 16
  • Зрізаний п'ятикутний трапецоедр^[en] — симетрія: D_5d^[en], порядок 20, топологічно еквівалентний до правильного додекаедра.

Примітки

1. Enumeration of Polyhedra - Numericana. www.numericana.com.
2. І.М. Фодчук, О.О. Ткач., с. 108.
3. Cotton, F. A. (1990). Chemical Applications of Group Theory, 3rd ed (PDF) (англ.) . New York: Wiley. с. 63.
4. Weisstein, Eric W. Pyritohedron(англ.) на сайті Wolfram MathWorld.
5. Pyritohedron(англ.) на сайті Polytope Wiki.
6. Л. О. Бірюкович, с. 234.
7. Wadsworth, M. Edward, с. 400.
8. Dutch, Steve. (1997). The 48 Special Crystal Forms (PDF) (англ.) . University of Wisconsin-Green Bay, U.S.
9. CRYSTAL HABIT. www.galleries.com.
10. The Tetartoid. Demonstrations.wolfram.com. Retrieved on 2016-12-02.
11. Hafner, I. and Zitko, T. Introduction to golden rhombic polyhedra. Faculty of Electrical Engineering, University of Ljubljana, Slovenia.
12. Lord, E. A.; Ranganathan, S.; Kulkarni, U. D. (2000). Tilings, coverings, clusters and quasicrystals. Curr. Sci. 78: 64—72.

Література

• І.М. Фодчук, О.О. Ткач. Основи кристалографії: навчальний посібник. — Чернівці : ЧНУ ім. Юрія Федьковича, 2007. — 108 с.

• Л. О. Бірюкович. Кристалографія, Кристалохімія та Мінералогія. Підручник. — Київ : КПІ ім. Ігоря Сікорського, 2018. — 234 с.

• Wadsworth, M. Edward. Crystallography : an elementary manual for the laboratory. — Philadelphia : J.J. McVey, 1909. — 400 с.

Посилання

• Weisstein, Eric W. Pyritohedron(англ.) на сайті Wolfram MathWorld.
• Pyritohedron(англ.) на сайті Polytope Wiki.
• Tetartoid(англ.) на сайті Polytope Wiki.