Трапеція

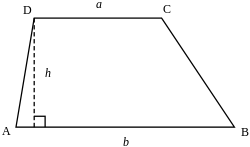
Трапе́ція (лат. trapezium, від дав.-гр. τραπέζιον — «столик») — це чотирикутник, дві протилежні сторони якого паралельні, а інші дві сторони — не паралельні^[1]. Паралельні сторони називаються основами трапеції (сторони AB та DC на малюнку). Інші сторони називаються бічними сторонами (сторони AD та CB).

У Вікіпедії є статті про інші значення цього терміна: Трапеція (значення).

Трапеція
Трапеція
Вид	Чотирикутник
Ребра і вершини	4
Площа	${\displaystyle {\tfrac {a+b}{2}}h}$
Властивості	Опуклий многокутник

Виділяють два класи трапецій:

• Рівнобічна трапеція, тобто трапеція у якої бічні сторони рівні.
• Прямокутна трапеція — це трапеція у якої два кута прямі.

Відрізок, який сполучає середини бічних сторін, називається середньою лінією трапеції. Середня лінія паралельна основам трапеції, а її довжина дорівнює їх півсумі:

${\displaystyle l={\frac {a+b}{2}}.}$

Відстань h між основами трапеції називається висотою трапеції.

Етимологія

Термін трапеція походить від дав.-гр. τραπέζιον, trapézion, буквально «столик» — зменшувальна форма від τράπεζα («стіл», звідки й «трапеза»), утвореного з τετράς («чотири») + πέζα («нога, ребро»)^[2]. У США і Канаді використовується термін trapezoid, що походить від τραπεζοειδή («столоподібний»); перше задокументоване вживання цього терміна трапляється у Прокла (412—485 н. е.) у його коментарі до першої книги «Начал» Евкліда^[3].

Основні види трапецій

Зображення до основних видів трапецій

Трапецію називають прямокутною, якщо у неї два сусідніх кути дорівнюють 90°.

Гострою називається трапеція у якої кути, прилеглі до більшої основи гострі (менше 90°).

Трапецію називають рівнобічною, якщо її бічні сторони та кути, прилеглі до більшої основи, рівні. Ця трапеція має осьову симетрію.

Тупою називається трапеція, у якої один із кутів, прилеглих до більшої основи, тупий (більше 90°).

Переважною є позиція, що окрім двох паралельних сторін, трапеція повинна мати дві непаралельні сторони^[1]. Проте іноді до трапецій включають всі паралелограми (ромби, прямокутники і квадрати), оскільки вони мають дві пари паралельних сторін. Прямокутники мають дзеркальну симетрію по середині ребер; ромби мають дзеркальну симетрію на вершинах, а квадрати мають дзеркальну симетрію з обох середніх ребер і вершин.

Дотичною називається трапеція, яка має вписане коло.

Властивості

Для будь-якого опуклого чотирикутника такі властивості еквівалентні, і кожна передбачає, що чотирикутник є трапецією:

• Сума двох кутів, прилеглих до бічних ребер, дорівнює 180°.
• Кут між однією основою і діагоналлю дорівнює куту між іншою основою та тією ж діагоналлю (внутрішні різносторонні кути рівні).
• Середня лінія трапеції паралельна основам і дорівнює їх півсумі.
• Точка перетину діагоналей трапеції, точка перетину продовжень її бічних сторін та середини основ лежать на одній прямій.
• Трикутники, утворені відрізками діагоналей та основами трапеції, подібні.
• Трикутники, утворені відрізками діагоналей та бічними сторонами трапеції, мають однакову площу.
• Відрізок, що з'єднує середини діагоналей, дорівнює піврізниці основ і лежить на середній лінії.
• Бісектриса будь-якого кута трапеції відтинає на її основі (або продовженні) відрізок, рівний бічній стороні.
• Якщо сума кутів при будь-якій основі трапеції дорівнює 90°, то відрізок, що з'єднує середини основ, дорівнює їх піврізниці.
• Якщо сума основ трапеції дорівнює сумі її бічних сторін, то в таку трапецію можна вписати коло, і навпаки.
• Будь-яку трапецію можна побудувати за довжинами чотирьох сторін.
• В рівнобічній трапеції:
  • кути при основі, а також діагоналі рівні
  • якщо діагоналі рівнобічної трапеції перпендикулярні, то висота такої трапеції дорівнює півсумі основ
• Навколо рівнобічної трапеції можна описати коло.

Висота трапеції

Схематичні зображення до формул.

Висота — перпендикулярна відстань між основами. У разі, коли дві основи мають різну довжину (а ≠ b), висота трапеції може бути визначена через довжини чотирьох сторін за формулою:

${\displaystyle h={\frac {\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}{2|b-a|}}}$,

де a, b — основи трапеції, а c і d — бічні сторони. Формула висоти трапеції, виражена через бокові сторони та кути, що прилеглі до більшої основи:

${\displaystyle h=c\cdot \sin \alpha =d\cdot \sin \beta }$

Формула висоти трапеції, виражена через діагоналі та кути між ними:

${\displaystyle h={\frac {d_{1}\cdot d_{2}}{a+b}}\cdot \sin \alpha ={\frac {d_{1}\cdot d_{2}}{a+b}}\cdot \sin \beta }$.

Формула висоти трапеції, виражена через площу:

${\displaystyle h={\frac {2S}{a+b}}={\frac {S}{m}}}$, де S — площа трапеції, m — середня лінія.

Площа трапеції

Площа трапеції дорівнює добутку півсуми основ на висоту:

${\displaystyle S={\frac {a+b}{2}}h=lh}$

Коли відомі довжини всіх чотирьох сторін трапеції, можемо використовувати іншу формулу визначення площі. Якщо позначити основи трапеції ${\displaystyle a}$ та ${\displaystyle b}$ (${\displaystyle b>a}$), а бічні сторони ${\displaystyle c}$ та ${\displaystyle d}$, то

${\displaystyle S={\frac {1}{4}}{\frac {b+a}{b-a}}{\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}}$.

Або:

${\displaystyle S={\frac {a+b}{2}}{\sqrt {c^{2}-\left({\frac {(b-a)^{2}+c^{2}-d^{2}}{2(b-a)}}\right)^{2}}}}$.

В 499 році н. е. Аріабхата, великий математик-астроном з класичної епохи індійської математики та індійської астрономії, використовував окремий випадок добре відомої формули для площі трикутника, розглядаючи трикутник як вироджену трапецію, у якої одна з паралельних сторін стиснулася до точки. У такому випадку формула для находження площі зводиться до формули Герона для площі трикутника.

Інша еквівалентна формула для площі, яка ближче нагадує формулу Герона, є:

${\displaystyle S={\frac {a+b}{|b-a|}}{\sqrt {(s-b)(s-a)(s-b-c)(s-b-d)}},}$ де ${\displaystyle s={\tfrac {1}{2}}(a+b+c+d)}$ — півпериметр трапеції.

Площа рівнобічної трапеції з радіусом вписаного кола ${\displaystyle r}$ та кутом при основі ${\displaystyle \alpha }$:

${\displaystyle S={\frac {4r^{2}}{\sin {\alpha }}}.}$

Діагоналі

Довжину діагоналей трапеції можна обчислити за формулами:

${\displaystyle p={\sqrt {\frac {ab^{2}-a^{2}b-ac^{2}+bd^{2}}{b-a}}},}$

${\displaystyle q={\sqrt {\frac {ab^{2}-a^{2}b-ad^{2}+bc^{2}}{b-a}}},}$

де a, b — основи трапеції, а c і d — бічні сторони.

Якщо трапеція ділиться діагоналями AC і BD, що перетинаються в точці О, на чотири трикутники (як показано праворуч), то площа трикутника ΔAOD дорівнює площі трикутника ΔBOC, і добуток площ трикутників ΔAOD і ΔBOC дорівнює добутку площ трикутників ΔАОВ і ΔCOD. Відношення площ кожної пари суміжних трикутників таке ж, що між довжинами паралельних сторін.

Діагоналі трапеції ${\displaystyle d_{1}}$ та ${\displaystyle d_{2}}$ пов'язані зі сторонами співвідношенням:

${\displaystyle d_{1}^{2}+d_{2}^{2}=2ab+c^{2}+d^{2}}$.

Їх можна знайти за формулами:

${\displaystyle d_{1}=AC={\sqrt {ab+d^{2}+{\frac {b(c^{2}-d^{2})}{b-a}}}}}$

${\displaystyle d_{2}=BD={\sqrt {ab+c^{2}-{\frac {b(c^{2}-d^{2})}{b-a}}}}}$

Також діагоналі можна знайти через висоту трапеції за наступними формулами:

${\displaystyle d_{1}={\sqrt {b^{2}+d^{2}-2b{\sqrt {d^{2}-h^{2}}}}}={\sqrt {h^{2}+\left(b-{\sqrt {d^{2}-h^{2}}}\right)^{2}}}}$

${\displaystyle d_{2}={\sqrt {b^{2}+c^{2}-2b{\sqrt {c^{2}-h^{2}}}}}={\sqrt {h^{2}+\left(b-{\sqrt {c^{2}-h^{2}}}\right)^{2}}}}$

Використовування в архітектурі

Храм Дендур^[en] у музеї мистецтва Метрополітен у Нью-Йорку

В архітектурі слово трапеція використовується для позначення симетричних дверей, вікон і будівель, побудованих ширше біля основи, звужених до вершини (в єгипетському стилі). Існує чимало будівель, що мають форму рівнобічної трапеції. Це був стандартний стиль для дверей і вікон у інків.^[4]

Примітки

1. Математичний словник | Математика, логіка, інтелект. formula.co.ua. Архів оригіналу за 15 січня 2019. Процитовано 14 січня 2019.
2. Henry George Liddell, Robert Scott, Henry Stuart Jones, A Greek-English Lexicon, Oxford, Clarendon Press (1940), s.v. πέζα [Архівовано 28 квітня 2021 у Wayback Machine.], τράπεζα [Архівовано 13 квітня 2019 у Wayback Machine.]
3. Oxford English Dictionary entry at trapezoid.
4. Архівована копія. Архів оригіналу за 9 червня 2016. Процитовано 24 травня 2016.{{cite web}}: Обслуговування CS1: Сторінки з текстом «archived copy» як значення параметру title (посилання)

Див. також

• Рівнобічна трапеція
• Чотирикутник
• Квадрат

Посилання

• Трапеція // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.
• http://easycalculation.com/area/trapezium.php [Архівовано 2 січня 2010 у Wayback Machine.]
• Trapezium [Архівовано 12 жовтня 2017 у Wayback Machine.] at Encyclopedia of Mathematics.
• Weisstein, Eric W. Right trapezoid(англ.) на сайті Wolfram MathWorld.
• Trapezoid definition [Архівовано 17 вересня 2018 у Wayback Machine.]   Area of a trapezoid [Архівовано 13 жовтня 2017 у Wayback Machine.]   Median of a trapezoid [Архівовано 13 жовтня 2017 у Wayback Machine.] With interactive animations
• Trapezoid (North America) [Архівовано 28 жовтня 2008 у Wayback Machine.] at elsy.at: Animated course (construction, circumference, area)
• Trapezoidal Rule [Архівовано 3 лютого 2009 у Wayback Machine.] on Numerical Methods for Stem Undergraduate
• Autar Kaw and E. Eric Kalu, Numerical Methods with Applications [Архівовано 4 серпня 2020 у Wayback Machine.], (2008)