Распределение Пуассона

Распределе́ние Пуассо́на — распределение дискретного типа случайной величины, представляющей собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Распределение Пуассона
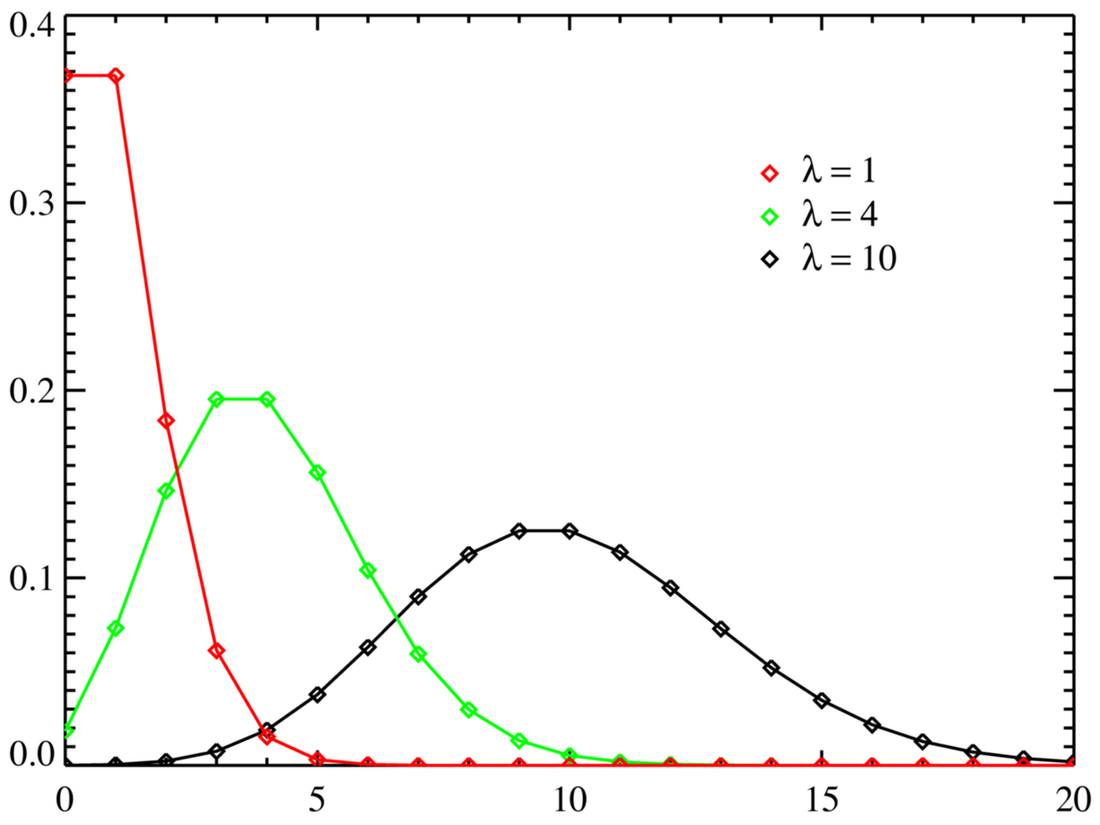
Функция вероятности
Функция распределения
Обозначение	${\displaystyle \mathrm {P} (\lambda )}$
Параметры	${\displaystyle \lambda \in (0,\infty )}$
Носитель	${\displaystyle k\in \{0,1,2,\ldots \}}$
Функция вероятности	${\displaystyle {\frac {e^{-\lambda }\lambda ^{k}}{k!}}}$
Функция распределения	${\displaystyle {\frac {\Gamma (k+1,\lambda )}{k!}}}$
Математическое ожидание	${\displaystyle \lambda }$
Медиана	${\displaystyle \approx \lfloor \lambda +1/3-0.02/\lambda \rfloor }$
Мода	${\displaystyle \lfloor \lambda \rfloor }$, ${\displaystyle \lfloor \lambda \rfloor }$ - 1
Дисперсия	${\displaystyle \lambda }$
Коэффициент эксцесса	${\displaystyle \lambda ^{-1}}$
Дифференциальная энтропия	${\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\ln(k!)}{k!}}}$
Производящая функция моментов	${\displaystyle \exp(\lambda (e^{t}-1))}$
Характеристическая функция	${\displaystyle \exp(\lambda (e^{it}-1))}$

Распределение Пуассона играет ключевую роль в теории массового обслуживания.

Определение

Выберем фиксированное число ${\displaystyle \lambda >0}$ и определим дискретное распределение, задаваемое следующей функцией вероятности:

${\displaystyle p(k)\equiv \mathbb {P} (Y=k)={\frac {\lambda ^{k}}{k!}}\,e^{-\lambda }}$,

где

• ${\displaystyle k}$ — количество событий,
• ${\displaystyle \lambda }$ — математическое ожидание случайной величины (среднее количество событий за фиксированный промежуток времени),
• ${\displaystyle k!}$ обозначает факториал числа ${\displaystyle k}$,
• ${\displaystyle e=2{,}718281828\ldots }$ — основание натурального логарифма.

Тот факт, что случайная величина ${\displaystyle Y}$ имеет распределение Пуассона с математическим ожиданием ${\displaystyle \lambda }$, записывается: ${\displaystyle Y\sim ~\mathrm {P} (\lambda )}$ или ${\displaystyle Y\sim \mathrm {Pois} (\lambda )}$.

Моменты

Производящая функция моментов распределения Пуассона имеет вид:

${\displaystyle E_{Y}(t)=e^{\lambda \left(e^{t}-1\right)}}$,

откуда

${\displaystyle \mathbb {M} [Y]=\lambda }$,

${\displaystyle \mathbb {D} [Y]=\lambda }$.

Для момента ${\displaystyle k}$-го порядка справедлива общая формула:

${\displaystyle \mathbb {M} Y^{k}=\sum _{i=0}^{k}\lambda ^{i}\left\{{\begin{matrix}k\\i\end{matrix}}\right\}}$,

где ${\displaystyle k=1,2,...}$. Фигурные же скобки обозначают числа Стирлинга второго рода.

А так как моменты и факториальные моменты линейным образом связаны, то часто для пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.

Свойства распределения Пуассона

• Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть ${\displaystyle Y_{i}\sim \mathrm {P} (\lambda _{i}),\;i=1,\ldots ,n}$. Тогда

${\displaystyle Y=\sum \limits _{i=1}^{n}Y_{i}\sim \mathrm {P} \left(\sum \limits _{i=1}^{n}\lambda _{i}\right)}$.

• Пусть ${\displaystyle Y_{i}\sim \mathrm {P} (\lambda _{i}),\;i=1,2}$, и ${\displaystyle Y=Y_{1}+Y_{2}}$. Тогда условное распределение ${\displaystyle Y_{1}}$ при условии, что ${\displaystyle Y=y}$, биномиально. Более точно:

${\displaystyle Y_{1}\mid Y=y\sim \mathrm {Bin} \left(y,{\frac {\lambda _{1}}{\lambda _{1}+\lambda _{2}}}\right)}$.

• C увеличением ${\displaystyle \lambda }$ распределение Пуассона стремится к распределению Гаусса со среднеквадратичным отклонением ${\displaystyle \sigma ={\sqrt {\lambda }}}$ и сдвигом ${\displaystyle \lambda }$. Чтобы доказать это, нужно применить формулу Стирлинга для факториала, а затем воспользоваться разложением в ряд Тейлора ${\displaystyle \ln(\lambda /k)^{k}}$ в окрестности ${\displaystyle k=\lambda }$ и тем, что в пределах пика распределения ${\displaystyle {\sqrt {k}}\approx {\sqrt {\lambda }}}$. Тогда получается

${\displaystyle p(k)\approx {\frac {1}{\sqrt {2\pi \lambda }}}\exp \left(-{\frac {(k-\lambda )^{2}}{2\lambda }}\right)}$

• Производящая функция распределения Пуассона выглядит так: ${\displaystyle \exp \left[\lambda \left(z-1\right)\right]}$

Асимптотическое стремление к распределению

Довольно часто в теории вероятностей рассматривают не само распределение Пуассона, а последовательность распределений, асимптотически равных ему. Более формально, рассматривают последовательность случайных величин ${\displaystyle \xi _{1},\xi _{2},\dots }$, принимающих целочисленные значения, такую что для всякого ${\displaystyle k}$ выполнено ${\displaystyle P\{\xi _{n}=k\}\sim {\frac {\lambda ^{k}e^{-\lambda }}{k!}}}$ при ${\displaystyle n\to \infty }$.

Простейшим примером является случай, когда ${\displaystyle \xi _{n}}$ имеет биномиальное распределение с вероятностью успеха ${\displaystyle {\frac {\lambda }{n}}}$ в каждом из ${\displaystyle n}$ испытаний.

Обратная связь с факториальными моментами

Рассмотрим последовательность случайных величин ${\displaystyle \xi _{1},\xi _{2},\dots }$, принимающих целые неотрицательные значения. Если ${\displaystyle \mu _{r}({\xi _{n}})\sim \lambda ^{r}}$ при ${\displaystyle n\to \infty }$ и любом фиксированном ${\displaystyle r}$ (где ${\displaystyle \mu _{r}({\xi _{n}})}$ — ${\displaystyle r}$-й факториальный момент), то для всякого ${\displaystyle k}$ при ${\displaystyle n\to \infty }$ выполнено ${\displaystyle P\{\xi _{n}=k\}\sim {\frac {\lambda ^{k}e^{-\lambda }}{k!}}}$.

Доказательство

Лемма

Для начала докажем общую формулу вычисления вероятности появления конкретного значения случайной величины через факториальные моменты. Пусть для некоторого ${\displaystyle \xi }$ известны все ${\displaystyle \mu _{r}(\xi )}$ и ${\displaystyle \mu _{r}(\xi )\to 0}$ при ${\displaystyle r\to \infty }$. Тогда

${\displaystyle \sum \limits _{r=k}^{\infty }{(-1)^{r-k}{\frac {\mu _{r}(\xi )}{k!(r-k)!}}}=\sum \limits _{r=k}^{\infty }{\sum \limits _{s=r}^{\infty }{(-1)^{r-k}{\frac {s!}{k!(r-k)!(s-r)!}}P\{\xi =s\}}}.}$

Изменяя порядок суммирования, это выражение можно преобразовать в

${\displaystyle \sum \limits _{s=k}^{\infty }{P\{\xi =s\}\sum \limits _{r=k}^{s}{\frac {(-1)^{r-k}s!}{k!(r-k)!(s-r)!}}}=\sum \limits _{s=k}^{\infty }{P\{\xi =s\}{\frac {s!}{k!}}\sum _{t=0}^{s-k}{\frac {(-1)^{t}}{t!((s-k)-t)!}}}.}$

Далее, из известной формулы ${\displaystyle \sum \limits _{k=0}^{n}{(-1)^{k}C_{n}^{k}}=0}$ получаем, что ${\displaystyle {\frac {s!}{k!}}\sum _{t=0}^{s-k}{\frac {(-1)^{t}}{t!((s-k)-t)!}}=0}$ при ${\displaystyle s>k}$ и то же выражение вырождается в ${\displaystyle 1}$ при ${\displaystyle s=k}$.

Тем самым доказано, что ${\displaystyle P\{\xi =k\}=\sum \limits _{r=k}^{\infty }{(-1)^{r-k}{\frac {\mu _{r}(\xi )}{k!(r-k)!}}}.}$

Доказательство теоремы

Согласно лемме и условиям теоремы, ${\displaystyle P\{\xi _{n}=k\}\sim \sum \limits _{r=k}^{\infty }{(-1)^{r-k}{\frac {\lambda ^{r}}{k!(r-k)!}}}=\sum \limits _{r=0}^{\infty }{(-1)^{r}{\frac {\lambda ^{r+k}}{k!r!}}}={\frac {\lambda ^{k}}{k!}}\sum \limits _{r=0}^{\infty }{\frac {(-\lambda )^{r}}{r!}}={\frac {\lambda ^{k}e^{-\lambda }}{k!}}}$ при ${\displaystyle n\to \infty }$.

Q.E.D.

Как пример нетривиального следствия этой теоремы можно привести, например, асимптотическое стремление к ${\displaystyle \mathrm {P} (\lambda )}$ распределения количества изолированных рёбер (двухвершинных компонент связности) в случайном ${\displaystyle n}$-вершинном графе, где каждое из рёбер включается в граф с вероятностью ${\displaystyle p_{n}\sim {\frac {2\lambda }{n^{2}}}}$.^[1]

История

Работа Симеона Дени Пуассона «Исследования о вероятности приговоров в уголовных и гражданских делах»^[2], в которой было введено данное распределение, была опубликована в 1837 году^[3]. Примеры других ситуаций, которые можно смоделировать, применив это распределение: поломки оборудования, длительность исполнения ремонтных работ стабильно работающим сотрудником, ошибка печати, рост колонии бактерий в чашке Петри, дефекты в длинной ленте или цепи, импульсы счётчика радиоактивного излучения, количество забиваемых футбольной командой голов и др.^[4]

См. также

• Биномиальное распределение
• Обобщенное распределение Пуассона на локально компактной абелевой группе

Примечания

1. Видеолекция Школы Анализа Данных  (неопр.). Дата обращения: 7 декабря 2014. Архивировано 8 апреля 2014 года.
2. Пуассон, 1837.
3. Чукова Ю. П.  Распределение Пуассона // «Квант» : науч.-поп. физ.-мат. журн. — М.: «Наука», 1988. — № 8. — С. 15‒18. — ISSN 0130-2221.
4. Винс, 2012, с. 370.

Литература

• Вентцель Е. С., Овчаров Л. А. Теория вероятностей и её инженерные приложения. 2-е изд. — М.: Высшая школа, 2000. — 480 с. — ISBN 978-5-406-00565-1. — С. 135.
• Винс, Ральф. Математика управления капиталом: Методы анализа риска для трейдеров и портфельных менеджеров = The mathematics of money management risk analysis techniques for traders. — М.: Альпина Паблишер, 2012. — 400 с. — ISBN 978-5-9614-1894-1.
• Пуассон С. Д. Исследования о вероятности приговоров в уголовных и гражданских делах = Poisson S.-D. Recherches sur la probabilité des jugements en matière criminelle et en matière civile. — Berlin: NG Verlag (Viatcheslav Demidov Inhaber), 2013. — 330 p. — ISBN 978-3-942944-29-8. [Poisson.pdf]  (неопр.). Архивировано 1 ноября 2014 года.
• Guerriero V. Power Law Distribution: Method of Multi-scale Inferential Statistics. — Journal of Modern Mathematics Frontier, 2012, 1. — P. 21—28. Архивная копия от 21 февраля 2018 на Wayback Machine

Ссылки

• Распределение Пуассона — онлайн-калькулятор