Функция распределения

Не следует путать с Функция распределения (статистическая физика).

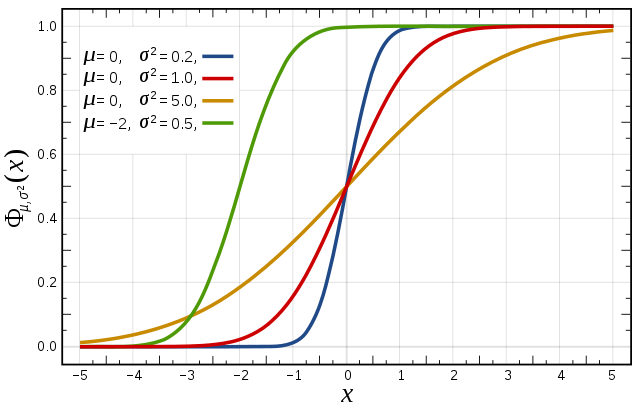
Фу́нкция распределе́ния в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора. В одномерном случае функция распределения — это вероятность того, что случайная величина ${\displaystyle X}$ примет значение, меньшее ${\displaystyle x}$, где ${\displaystyle x}$ — произвольное действительное число^{[1][2][3][4][5]}.

Функции распределения гауссовых случайных величин.

Определение

Пусть дано вероятностное пространство ${\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}$, и на нём определена случайная величина ${\displaystyle X}$ с распределением ${\displaystyle \mathbb {P} ^{X}}$. Тогда функцией распределения случайной величины ${\displaystyle X}$ называется функция ${\displaystyle F_{X}}$, задаваемая формулой^{[1][2][3][4][5]}:

${\displaystyle F_{X}(x)=\mathbb {P} (X<x)\equiv \mathbb {P} ^{X}\left((-\infty ,x)\right)}$.

То есть функцией распределения (вероятностей) случайной величины ${\displaystyle X}$ называют функцию ${\displaystyle F(x)}$, значение которой в точке ${\displaystyle x}$ равно вероятности события ${\displaystyle \{X<x\}}$, то есть события, состоящего только из тех элементарных исходов, для которых ${\displaystyle X<x}$.

Свойства

• ${\displaystyle F_{X}}$ непрерывна слева^[6]:

  ${\displaystyle \lim \limits _{x\to x_{0}-}F_{X}(x)=F_{X}(x)}$

• ${\displaystyle F_{X}}$ не убывает на всей числовой прямой.
• ${\displaystyle \lim \limits _{x\to -\infty }F_{X}(x)=0}$.
• ${\displaystyle \lim \limits _{x\to +\infty }F_{X}(x)=1}$.

Если функция ${\displaystyle F(x)}$ удовлетворяет четырём перечисленным выше свойствам, то существует вероятностное пространство и определённая на нём случайная величина, такая что ${\displaystyle F(x)}$ является её функцией распределения^[6].

Функция ${\displaystyle F_{X}}$ была бы непрерывна справа^[6]:

${\displaystyle \lim \limits _{x\to x_{0}+}F_{X}(x)=F_{X}(x)}$,

если бы определение функции распределения было бы следующее:

${\displaystyle F_{X}(x)=\mathbb {P} (X\leqslant x)}$.

Такое определение функции распределения используется реже^[3][7], например у математика Ширяева А. Н.^[8]

Тождества

Из свойств вероятности следует, что ${\displaystyle \forall x\in \mathbb {R} ,\;\forall a,b\in \mathbb {R} }$, таких что ${\displaystyle a<b}$^[2][5]:

• ${\displaystyle \mathbb {P} (a\leqslant X\leqslant b)=F_{X}(b+0)-F_{X}(a)}$;
• ${\displaystyle \mathbb {P} (a\leqslant X<b)=F_{X}(b-0)-F_{X}(a)}$;

Дискретные распределения

Если случайная величина ${\displaystyle X}$ дискретна, то есть её распределение однозначно задаётся функцией вероятности:

${\displaystyle \mathbb {P} (X=x_{i})=p_{i},\;i=1,2,\ldots }$,

то функция распределения ${\displaystyle F_{X}}$ этой случайной величины кусочно-постоянна и может быть записана как:

${\displaystyle F_{X}(x)=\sum \limits _{i\colon x_{i}<x}p_{i}}$.

Эта функция непрерывна во всех точках ${\displaystyle x\in \mathbb {R} }$, таких что ${\displaystyle x\not =x_{i},\;\forall i}$, и имеет разрыв первого рода в точках ${\displaystyle x=x_{i},\;\forall i}$.

Непрерывные распределения

Распределение ${\displaystyle \mathbb {P} ^{X}}$ называется непрерывным, если такова его функция распределения ${\displaystyle F_{X}}$. В этом случае:

${\displaystyle \mathbb {P} (X=x)=0,\;\forall x\in \mathbb {R} }$,

и

${\displaystyle F_{X}(x-0)=F_{X}(x+0)=F_{X}(x),\;\forall x\in \mathbb {R} }$,

а следовательно формулы имеют вид:

${\displaystyle \mathbb {P} (X\in |a,b|)=F_{X}(b)-F_{X}(a)}$,

где ${\displaystyle |a,b|}$ означает любой интервал, открытый или закрытый, конечный или бесконечный^[9].

Абсолютно непрерывные распределения

Распределение ${\displaystyle \mathbb {P} ^{X}}$ называется абсолютно непрерывным, если существует неотрицательная почти всюду функция ${\displaystyle f_{X}(x)}$, такая что:

${\displaystyle F_{X}(x)=\int \limits _{-\infty }^{x}\!f_{X}(t)\,dt}$.

Функция ${\displaystyle f_{X}}$ называется плотностью распределения. Известно, что функция распределения абсолютно непрерывного распределения непрерывна, и, более того, если ${\displaystyle f_{X}\in C(\mathbb {R} )}$, то ${\displaystyle F_{X}\in {\mathcal {D}}(\mathbb {R} )}$, и

${\displaystyle {\frac {d}{dx}}F_{X}(x)=f_{X}(x),\;\forall x\in \mathbb {R} }$.

Вариации и обобщения

Многомерные функции распределения

Пусть ${\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}$ фиксированное вероятностное пространство, и ${\displaystyle X=(X_{1},\ldots ,X_{n})\colon \Omega \to \mathbb {R} ^{n}}$ — случайный вектор. Тогда распределение ${\displaystyle \mathbb {P} ^{X}}$, называемое распределением случайного вектора ${\displaystyle X}$ или совместным распределением случайных величин ${\displaystyle X_{1},\ldots ,X_{n}}$, является вероятностной мерой на ${\displaystyle \mathbb {R} ^{n}}$. Функция этого распределения ${\displaystyle F_{X}}$ задаётся по определению следующим образом:

${\displaystyle F_{X}(x_{1},\ldots ,x_{n})=\mathbb {P} (X_{1}<x_{1},\ldots ,X_{n}<x_{n})\equiv \mathbb {P} ^{X}\left(\prod \limits _{i=1}^{n}(-\infty ,x_{i})\right)}$,

где ${\displaystyle \prod }$ в данном случае обозначает декартово произведение множеств.

Свойства многомерных функций распределения аналогичны одномерному случаю. Также сохраняется взаимно-однозначное соответствие между распределениями на ${\displaystyle \mathbb {R} ^{n}}$ и многомерными функциями распределения. Однако, формулы для вычисления вероятностей существенно усложняются, и потому функции распределения редко используются для ${\displaystyle n>1}$.

См. также

• Плотность вероятности