Loading AI tools
Из Википедии, свободной энциклопедии
В математике абстрактный многогранник, неформально говоря, это структура, которая учитывает только комбинаторные свойства традиционных многогранников и игнорирует много других их свойств, таких как углы, длины рёбер и т. д. При этом не требуется наличие какого-либо содержащего многогранник пространства, такого как евклидово пространство. Абстрактная формулировка реализует комбинаторные свойства как частично упорядоченное множество («посет»[1]).

Абстрактное определение позволяет некоторые более общие комбинаторные структуры, чем традиционная концепция многогранника, и допускает много новых объектов, не имеющих аналога в традиционной теории.
В евклидовой геометрии шесть четырёхугольников на рисунке выше различны. Всё же они имеют что-то общее, что отличает их от треугольника или куба, например.
Элегантная, хотя географически неточная, схема Лондонского метро[англ.] обеспечивает всю относящуюся к делу информацию как проехать из пункта A в пункт B. Ещё лучший пример — электрическая принципиальная схема. По ней конечное расположение проводов и элементов часто с первого взгляда определить невозможно.
В каждом таком примере связи между элементами те же самые и не связаны с физическим расположением. В этом случае говорят, что объекты комбинаторно эквивалентны. Эта эквивалентность и заключена в понятие абстрактного многогранника. Таким образом, комбинаторно наши шесть четырёхугольников «те же самые». Говоря более строго, они изоморфны или «сохраняют структуру».
Свойства, в частности измеримые, традиционных многогранников, такие как углы, длина рёбер, несимметрия и выпуклость не имеют значения для абстрактных многогранников. Другие традиционные понятия могут рассматриваться, но не всегда тем же самым образом. Может случиться, что некоторое суждение, верное для традиционных многогранников, может не быть верным для абстрактных, и наоборот. Например, традиционные многогранники правильные, если все их грани и вершинные фигуры правильные, но это не имеет место для абстрактных многогранников[2].
Для определения абстрактных многогранников следует ввести несколько понятий.
В этой статье многогранник означает абстрактный многогранник, если не указано явно другое. Термин традиционный будет использоваться для ссылок на то, что обычно понимается под многогранниками за исключением собственно абстрактных многогранников. Иногда авторы употребляют термины классический или геометрический.
Связи на схеме железной дороги или электрической схеме могут быть представлены просто «точками и линиями», то есть графом. Многогранники, однако, имеют иерархию по размерности. Например, вершины, рёбра и грани куба имеют размерности 0, 1 и 2 соответственно. Сам куб является 3-мерным.
В этой абстрактной теории понятие ранга заменяет понятие размерности. Это понятие формально определено ниже.
Мы используем понятие грань для любых элементов любого ранга, например вершин (ранг 0) или рёбер (ранг 1), а не только граней ранга 2. Элемент ранга k называется k-гранью.
Можем тогда определить многогранник как множество граней P с отношением порядка <, которое удовлетворяет дополнительным аксиомам. Формально, P (с отношением порядка <) будет (строго) частично упорядоченным множеством (посет[1]).
Если F < G, мы говорим, что F является подгранью G (или G имеет подгрань F).
Мы говорим, что F и G инцидентны, если либо F = G, либо F < G, либо G < F. Это значение отличается от традиционного использования в геометрии и других областей математики. Например, в квадрате abcd, рёбра ab и bc не инцидентны.
Так же как понятия нуля и бесконечности являются необходимыми в математике, такие же понятия крайне полезны для абстрактных многогранников — считается что любой многогранник имеет наименьшую грань, являющуюся подгранью всех других, и наибольшую грань, для которой все остальные грани являются подгранями.
Фактически, многогранник может иметь всего одну грань. В этом случае наименьшая и наибольшая грани совпадают.
Наименьшая и наибольшая грани называются несобственными. Все остальные грани называются собственными.
Наименьшая грань называется пустой гранью, поскольку не имеет вершин (или каких-либо других граней) в качестве подграней. Поскольку наименьшая грань находится ниже по уровню вершин (граней нулевого ранга), её ранг равен −1. Мы обозначаем эту грань как F−1. Если это кажется на первый взгляд странным, это чувство быстро исчезает, когда понимаешь, какую симметрию это понятие вносит в теорию. (Исторически, математики сопротивлялись таким понятиям, как отрицательные числа, дробные, иррациональные и комплексные числа, и даже нулю!)
В качестве примера теперь создадим абстрактный квадрат с гранями как в таблице:
| Тип грани | Ранг (k) | Число | k-грани |
|---|---|---|---|
| Наименьшая | −1 | 1 | F−1 |
| Вершины | 0 | 4 | a, b, c, d |
| Рёбра | 1 | 4 | W, X, Y, Z |
| Наибольшая | 2 | 1 | G |
Отношение < определяется как множество пар, которое (для этого примера) включает
В этом примере мы могли бы записать рёбра W, X, Y и Z как ab, ad, bc и cd соответственно, и мы будем часто использовать такой вариант записи. Но, как мы вскоре увидим, такая система записи не всегда приемлема.
Мы называем полученную фигуру квадратом, а не четырёхугольником (или четырёхсторонником), поскольку в нашем абстрактном мире нет углов и рёбра не имеют длин. Все четыре ребра идентичны и «геометрия» в каждой вершине та же самая.
Отношения порядка транзитивны, т. е. из F < G и G < H следует, что F < H. Таким образом, для описания иерархии граней нет необходимости задавать все случаи F < H, достаточно указать для каждого элемента последующий элемент, т. е. когда F < H и нет такого G, для которого F < G < H.

Малые посеты, и многогранники в частности, часто хорошо визуализируются с помощью диаграммы Хассе, как показано на рисунке. Обычно грани одинакового ранга размещаются на одном горизонтальном уровне. Каждая «линия» между гранями соответствует паре F, G, такой что F < G, где F находится на диаграмме ниже, чем G.
Многогранник часто рисуется неформально как граф. Граф имеет вершины и рёбра, но не имеет граней. Более того, для большинства многогранников невозможно получить все остальные грани из графа, и, в общем случае, различные многогранники могут иметь тот же самый граф.
Диаграмма Хассе, с другой стороны, полностью описывает любой посет — все структуры многогранников покрываются диаграммами Хассе. Изоморфные многогранники дают изоморфные диаграммы Хассе и наоборот.
Ранг грани F определяется как целое (m − 2), где m — максимальное число граней в любой цепочке (F', F", ... , F), удовлетворяющей F' < F" < ... < F.
Ранг посета P — это максимальный ранг n любой грани, т. е. ранг максимальной грани (как указано выше, любой многогранник имеет максимальную грань). В этой статье мы всегда используем n для обозначения ранга посета или многогранника.
Отсюда следует, что наименьшая грань, и никакая другая, имеет ранг −1, а наибольшая грань имеет ранг n. Мы обозначаем их как F−1 и Fn соответственно.
Ранг грани или многогранника обычно соответствует размерности аналога в традиционной теории, но не всегда. Например, грань ранга 1 соответствует ребру, которое имеет размерность 1. Но пространственный многоугольник в традиционной геометрии является 3-мерным, поскольку он не является плоским. В абстрактном эквиваленте такой многоугольник остаётся абстрактным многоугольником ранга 2.
Для некоторых рангов существуют имена для типов граней.
| Ранг | −1 | 0 | 1 | 2 | 3 | … | n — 2 | n — 1 | n |
|---|---|---|---|---|---|---|---|---|---|
| Тип грани | Наимень- шая | Вершина | Ребро | † | Ячейка | Гиперребро | Гипергрань | Наибольшая |
† Хотя традиционно под «гранью» понимается грань ранга 2, мы будем всегда писать «2-грань» во избежание двусмысленности и оставляем термин «грань» для обозначения грани любого ранга.

Отрезок — это посет, имеющий минимальную грань, в точности две 0-грани и наибольшую грань, например {ø, a, b, ab}. Отсюда сразу следует, что вершины a и b имеют ранг 0, а наибольшая грань ab, а потому и сам посет, имеют ранг 1.
Флаг — это максимальная цепочка граней, то есть (полностью) упорядоченное множество Ψ граней, в котором каждая грань является подгранью следующей (если такова есть), и такое, что Ψ не является подмножеством какой-либо большей цепочки.
Например, {ø, a, ab, abc} является флагом в треугольнике abc.
Мы будем дополнительно требовать, чтобы для данного многогранника все флаги содержали одно и то же число граней. Посеты, в общем случае, не удовлетворяют этим требованиям. Посет {ø, a, b, bc, abc} имеет 2 флага неравного размера, а потому не является многогранником.
Ясно, что если есть две различные грани F, G во флаге, то либо F < G, либо F > G.

Любое подмножество P' посета P является посетом (с тем же отношение <, ограниченном на P').
В частности, если даны две грани F, H посета P, где F ≤ H, множество {G | F ≤ G ≤ H} называется секцией посета P и обозначается H/F. (В терминологии теории порядка секция носит название замкнутым интервалом посета и обозначается [F, H], но понятия идентичны).
Таким образом, P является секцией себя.
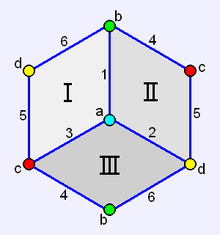
Например, в призме abcxyz (см. рисунок) секция xyz/ø (выделена зелёным цветом) является треугольником
k-секция — это секция ранга k.
Многогранник, являющийся подмножеством другого многогранника, не обязательно является секцией. Квадрат abcd является подмножеством тетраэдра abcd, но не является его секцией.
Понятие секции не имеет то же самое значение в традиционной геометрии.
Вершинная фигура в заданной вершине V — это (n−1)-секция Fn/V, где Fn является наибольшей гранью.
Например, в треугольнике abc вершинной фигурой в b, abc/b, является {b, ab, bc, abc}, то есть отрезок. Вершинными фигурами куба являются треугольники.
Посет P является связным, если ранг P ≤ 1, либо для любых двух собственных граней F и G существует последовательность собственных граней
Такая что F = H1, G = Hk и каждая грань Hi, i < k инцидентна предшествующей грани.
Условие выше обеспечивает, что пара отдельных треугольников abc и xyz не является (единым) многогранником.
Посет P является строго связным, если любая секция P (включая сам P) связна.
С этим дополнительным требованием исключаются две пирамиды, имеющие только общую вершину. Однако две квадратные пирамиды, например, могут быть «склеены» по их квадратным граням, что даёт октаэдр. В этом случае «общая грань» не является гранью октаэдра.
Абстрактный многогранник — это частично упорядоченное множество, элементы которого мы называем гранями, удовлетворяющий следующим четырём аксиомам:
n-многогранник является многогранником ранга n.
В случае пустого многогранника наименьшая и наибольшая грани являются одним и тем же единственным элементом.
Аксиома 2 эквивалентна утверждению, что посет является градуированным посетом.
Если выполняются другие аксиомы, аксиома 3 эквивалентна строгой связности флагов, что неформально означает:
Аксиома 4 известна как «свойство алмаза», поскольку на диаграмме Хассе отрезок представляется четырёхугольником (алмазом).
Из аксиом можно показать, что любая секция является многогранником и что Rank(G/F) = Rank(G) − Rank(F) − 1.
Имеется лишь по одному многограннику с рангами −1, 0 и 1, и это, соответственно, пустой многогранник, точка и отрезок.
Для n ≤ 1 все n-секции многогранника являются (уникальными) n-многогранниками. Однако грани ранга 0 и 1 многогранника называются вершинами и рёбрами соответственно.
Для любого p, 3 ≤ p < имеется (абстрактный эквивалент) традиционного многоугольника с p вершинами и p рёбрами, p-угольник. Для p = 3, 4, 5, … мы получаем треугольник, квадрат, пятиугольник, ….
Для p = 2 мы получим двуугольник, а для p = — апейрогон.

Дигон — это многогранник с двумя рёбрами, что соответствует имени. В отличие от других многоугольников, оба ребра имеют две общие вершины. По этой причине он считается вырожденным.
До сих пор мы использовали для определения граней «вершинную нотацию», например. {ø, a, b, c, ab, ac, bc, abc} для треугольника abc. Этот метод имеет определённое преимущество перед заданием отношения <.
В случае с дигоном и многими другими абстрактными многогранниками вершинную нотацию использовать нельзя. Мы вынуждены дать граням индивидуальные имена и указать пары подграней F < G (задать порядок).
Так, дигон должен быть определён как множество {ø, a, b, E', E", G} с отношением порядка <
где E' и E" — два ребра, а G — наибольшая грань.
Суммируя, многогранник может быть полностью описан лишь вершинной нотацией, если любая грань имеет уникальный набор вершин. Многогранник, имеющий такое свойство, называется атомарным[англ.].
Как отмечалось выше, понятие абстрактного многогранника является очень общим и включает:
В общем случае, множество j-граней (−1 ≤ j ≤ n) традиционного n-многогранника образует абстрактный n-многогранник.

Дигон обобщается осоэдрами, которые можно реализовать как сферические многогранники — замощения сферы.
Четырьмя примерами нетрадиционных абстрактных многогранников служат полукуб[англ.][3] (показан на рисунке), полуоктаэдр[англ.], полудодекаэдр и полуикосаэдр. Эти многогранники являются проективными двойниками правильных многогранников и могут быть реализованы как проективные многогранники[англ.] — они замощают вещественную проективную плоскость.
Полукуб служит ещё одним примером, когда вершинная нотация неприменима — все 2-грани и 3-грани имеют один и тот же набор вершин.
Любой многогранник имеет двойственный, многогранник, в котором частичный порядок обращён — диаграмма Хассе двойственного многогранника является той же, что и для оригинального, но перевёрнутая («вверх ногами»). Каждая исходная k-грань n-многогранника переходит в (n − k − 1)-грань двойственного. Так, например, n-грань переходит в (−1)-грань. Двойственный многогранник двойственному тождественен (изоморфен) исходному.
Многогранник является самодвойственным, если он совпадает со своим двойственным многогранником, то есть изоморфен двойственному. Таким образом, диаграмма Хассе самодвойственного многогранника должна быть симметрична относительно горизонтальной оси. Квадратная пирамида в примере выше является самодвойственным многогранником.
Вершинная фигура в вершине V является двойственной соответствующей грани двойственного многогранника.
Формально, абстрактный многогранник определяется как «правильный», если его группа автоморфизмов действует транзитивно на множество его флагов. В частности, любые две k-грани F и G n-многогранника являются «одинаковыми», то есть имеется автоморфизм, который переводит F в G. Когда абстрактный многогранник является правильным, его группа автоморфизмов изоморфна факторгруппе группы Коксетера.
Все многогранники ранга ≤ 2 правильные. Наиболее известные правильные многогранники — пять платоновых тел. Полукуб (показан на рисунке) является также правильным.
Неформально это означает, что для каждого ранга k нет путей отличить какую-либо k-грань от любой другой — грани должны быть одинаковыми и должны иметь одинаковых соседей, и так далее. Например, куб является правильным, поскольку все его грани являются квадратами, каждая вершина квадрата принадлежит трём квадратам и каждый квадрат окружён одинаково другими гранями, рёбрами и вершинами, и так далее.
Это условие без всяких дополнений достаточно для того, чтобы абстрактный многогранник имел изоморфные правильные (n−1)-грани и изоморфные правильные вершинные фигуры.
Это более слабое условие, чем правильность для традиционных многогранников, поскольку оно относится к (комбинаторной) группе автоморфизмов, а не (геометрической) группе симметрии. Например, любой абстрактный многоугольник является правильным, поскольку углы, длины рёбер, кривизна рёбер, перекос и т. д. не существуют для абстрактных многогранников.
Существуют некоторые другие ослабляющие понятия, некоторые не вполне стандартизованы, такие как полуправильный, квазиправильный, однородный, хиральный многогранники и архимедовы тела, которые применимы к многогранникам, в которых некоторые, но не все грани эквивалентны для каждого ранга.

Если принять во внимание, сколько места уделено правильным многогранникам, может показаться, что все многогранники правильны. В действительности, правильные многогранники являются очень специальными случаями.
Простейшим неправильным многогранником является квадратная пирамида, хотя она имеет много симметрий.
На рисунке приведён пример многогранника без нетривиальной симметрии — никакая пара вершин, рёбер, или 2-граней не являются «теми же самыми», как определено выше. Возможно, это самый простой из таких многогранников.
Любой традиционный многогранник является примером реализации его лежащего в основе абстрактного многогранника. То же самое для замощений плоскости или других кусочно линейных многообразий в размерностях два и выше. Последние включают, например, проективные многогранники. Они могут быть получены из многогранников с помощью центральной симметрии путём отождествления противоположных вершин, рёбер, граней и т. д. В трёхмерном пространстве это даёт полукуб[англ.] и полудодекаэдр и их двойственные, полуоктаэдр[англ.] и полуикосаэдр.
Более обще, реализация правильного абстрактного многогранника — это набор точек в пространстве (соответствующих вершинам многогранника), вместе со структурой граней, порождённой на них (абстрактным) многогранником, и эта структура, по меньшей мере, имеет те же симметрии, что и исходный абстрактный многогранник. То есть, все комбинаторные автоморфизмы абстрактных многогранников реализуются геометрическими симметриями. Например, набор точек {(0,0), (0,1), (1,0), (1,1)} является реализацией абстрактного 4-угольника (квадрата). Однако это не единственная реализация — можно выбрать вместо этого вершины правильного тетраэдра. Для любой симметрии квадрата существует соответствующая симметрия правильного тетраэдра (имеются, однако, больше симметрий у правильного тетраэдра, чем у абстрактного 4-угольника).
Фактически, любой абстрактный многогранник с v вершинами имеет по меньшей мере одну реализацию как вершины (v − 1)-мерного симплекса. Часто интересно найти реализацию в наименьшей размерности.
Если абстрактный n-многогранник реализуем в n-мерном пространстве так, что геометрическое расположение не нарушает каких-либо правил для традиционных многогранников (таких как криволинейные грани или гребни[4] нулевого размера), о такой реализации говорят как о правильной. В общем случае только ограниченное множество абстрактных многогранников ранга n могут быть реализованы правильно для любого n-пространства.
Базовая теория комбинаторных структур, которые теперь известны как «абстрактные многогранники» (первоначально называемые «incidence polytopes» — инциденциальные многогранники), описана в докторской диссертации Эгона Шульте, хотя она основывается на более ранних работах Бранко Грюнбаума, Гарольда Коксетера и Жака Титса. С тех пор исследования в теории абстрактных многогранников фокусировались, главным образом, на правильных многогранниках, то есть многогранниках, группы автоморфизмов которых действуют транзитивно на множестве флагов многогранника.
Важным вопросом в теории абстрактных многогранников является задача смешения. Задача состоит из серии вопросов, таких как
Например, если K квадрат, а L — треугольник, ответы на эти вопросы следующие
Известно, что если ответ на первый вопрос положителен (Да) для некоторых правильных K и L, существует единственный многогранник, гипергранями которого является K, а вершинными фигурами которого являются L. Этот многогранник называется универсальным многогранником с этими гипергранями и вершинными фигурами, который покрывает все многогранники этого типа. То есть, положим, что P является универсальным многогранником с гипергранями K и вершинными фигурами L. Тогда любой другой многогранник Q с этими гранями и вершинными фигурами можно записать как Q=P/N, где
Q=P/N называется частным от P, и мы говорим P покрывает Q.
Если учитывать этот факт, поиск многогранников с выбранными гипергранями и вершинными фигурами обычно идёт по следующему сценарию:
Эти две задачи, в общем случае, очень трудны.
Возвращаясь к примеру выше, если K является квадратом, а L — треугольником, универсальным многогранником {K,L} будет куб (который записывается как {4,3}). Полукуб является отношением {4,3}/N, где N — группа симметрий (автоморфизмов) с двумя элементами — тождественной симметрией и симметрией, отображающей каждый угол (ребро, или грань) в противоположный элемент.
Если L является также квадратом, универсальным многогранником {K,L} (то есть, {4,4}) является замощение евклидового пространства квадратами. Это замощение имеет бесконечное число частных с квадратными гранями, по четыре на вершину, некоторые из которых правильные, а некоторые — нет. За исключением самого универсального многогранника, все частные соответствуют различным путям замощения квадратами поверхности тора или бесконечно длинного цилиндра.
Одиннадцатиячейник, независимо открытый Коксетером и Грюнбаумом, является абстрактным 4-мерным многогранником. Его гранями служат полуикосаэдры. Поскольку гиперграни являются, топологически, проективными плоскостями, а не сферами, одиннадцатиячейник не является замощением какого-либо многообразия в привычном смысле. Вместо этого одиннадцатиячейник является локально проективным многогранником. Одиннадцатиячейник не только прекрасен в математическом отношении, он важен исторически как первый открытый нетрадиционный абстрактный многогранник. Многогранник самодвойственен и универсален — это единственный многогранник с полуикосаэдральными гипергранями и полудодекаэдральными вертексными фигурами.
Пятидесятисемиячейник[англ.] также самодвойственен, он имеет полудодекаэдральные гиперграни. Многогранник был найден Гарольдом Коксетером вскоре после открытия одиннадцатиячейника. Подобно одиннадцатиячейнику он универсален, будучи единственным многогранником с полудодекаэдральными гипергранями и полуикосаэдральными вершинными фигурами. С другой стороны, существует много других многогранников с полудодекаэдральными гипергранями и символом Шлефли {5,3,5}. Универсальный многогранник с полудодекаэдральными гипергранями и икосаэдральными (не полуикосаэдральными) вершинными фигурами конечен, но очень большой, он имеет 10006920 гиперграней и вдвое меньше вершин.
Задача слияния, исторически, относилась к локальной топологии. То есть, вместо ограничения K и L конкретными многогранниками, позволяются любые многогранники с заданной топологией, то есть любое замощение многогранниками заданного многообразия. Если K и L являются сферическими (то есть, замощения топологической сферы), то P называется локально сферическим и соответствует замощению некоторого многообразия. Например, если K и L являются оба квадратами (а потому, топологически, окружностями), P будет замощением плоскости, тора или бутылки Клейна квадратами. Замощение n-мерного многообразия, фактически, является многогранником ранга n + 1. И это согласуется с интуитивным представлением, что платоновы тела трёхмерны, даже если они могут рассматриваться как замощения поверхности двумерной поверхности шара.
В общем случае, абстрактный многогранник называется локально X, если его гиперграни и вершинные фигуры, топологически, либо сферы, либо X, но не сферы одновременно. Одиннадцатиячейник и пятидесятисемиячейник[англ.] являются примерами локально проективных многогранников ранга 4 (то есть, четырёхмерных), поскольку их гиперграни и вершинные фигуры являются замощениями вещественных проективных плоскостей. Здесь, однако, существует слабость терминологии. Определение не даёт простых путей описания многогранников, гипергранями которых являются торы, а вершинными фигурами — проективные плоскости, например. Ещё хуже, когда различные гиперграни имеют различную топологию или не имеют определённую топологию вообще. Однако большой шаг был сделан по полной классификации n локально тороидальных правильных многогранников[5].
Пусть Ψ — флаг абстрактного n-многогранника и пусть −1 < i < n. Из определения абстрактного многогранника можно доказать, что имеется единственный флаг, отличный от Ψ только одним элементом ранга i и тот же самый в остальном. Если мы обозначим такой флаг через Ψ(i), то это задаёт набор отображений флагов многогранника, скажем φi. Эти отображения называются отображениями обмена, поскольку они меняют местами пары флагов : (Ψφi)φi = Ψ[6]. Некоторые другие свойства отображений обмена :
Отображения обмена могут быть использованы для доказательства, что любой абстрактный многогранник является производным от некоторого правильного многогранника.
Многогранник можно представить в виде таблицы инциденций. Ниже приведена матрица инциденций для треугольника:
| ø | a | b | c | ab | bc | ca | abc | |
|---|---|---|---|---|---|---|---|---|
| ø | • | • | • | • | • | • | • | • |
| a | • | • | • | • | • | |||
| b | • | • | • | • | • | |||
| c | • | • | • | • | • | |||
| ab | • | • | • | • | • | |||
| bc | • | • | • | • | • | |||
| ca | • | • | • | • | • | |||
| abc | • | • | • | • | • | • | • | • |
Точка в таблице показывает, что одна грань является подгранью другой грани (или наоборот, так что таблица симметрична относительно диагонали). Таким образом, таблица содержит избыточную информацию, достаточно было бы показывать точку, когда номер грани строки ≤ номера грани столбца (верхнюю треугольную матрицу).
Поскольку само тело и пустое множество инцидентны всем другим элементам, первая строка и первый столбец, а также последняя строка и последний столбец тривиальны и могут быть опущены.
Дальнейшую информацию можно получить путём подсчёта инциденций. Такое численное представление позволяет группировку по симметрии как в диаграмме Хассе квадратной пирамиды — если вершины B, C, D и E эквивалентны по симметрии в абстрактном многограннике, то рёбра f, g, h и j группируются вместе, и то же самое для рёбер k, l, m и n. В конечном счёте группируются и треугольники 'P', 'Q', 'R' и 'S'. Соответствующая матрица инциденций абстрактного многогранника может выглядеть следующим образом:
| A | B,C,D,E | f, g, h, j | k, l, m, n | P,Q,R,S | T | |
|---|---|---|---|---|---|---|
| A | 1 | * | 4 | 0 | 4 | 0 |
| B,C,D,E | * | 4 | 1 | 2 | 2 | 1 |
| f, g, h, j | 1 | 1 | 4 | * | 2 | 0 |
| k, l, m, n | 0 | 2 | * | 4 | 1 | 1 |
| P,Q,R,S | 1 | 2 | 2 | 1 | 4 | * |
| T | 0 | 4 | 0 | 4 | * | 1 |
В этой матрице инциденций диагональные элементы дают общее число каждого типа элемента.
Ясно, что элементы различных типов одного ранга никогда не могут быть инцидентны, так что значение всегда равно 0, но чтобы помочь распознать это отношение в таблице используется звёздочка (*) вместо нуля.
Поддиагональные элементы таблицы для каждой строки представляют число инциденций соответствующих подэлементов, в то время как наддиагональные элементы представляют число инциденций элемента вершинам, рёбрам и другим фигурам.
Уже этот пример квадратной пирамиды показывает, что такая матрица инцидентности не симметрична. Однако остаются простые связи элементов таблицы, поскольку для таких матриц инцидентности выполняется:
Ранние примеры абстрактных многогранников обнаружили Коксетер и Петри — три бесконечные структуры {4, 6}, {6, 4} и {6, 6}, которые они назвали правильными косыми бесконечногранниками[англ.].
В 1960-м Бранко Грюнбаум предложил геометрическому сообществу обсудить обобщение понятия правильных многогранников, которые он назвал polystromata (poly + stromata[7]). Он разработал теорию, показав примеры новых объектов, включая одиннадцатиячейник.
Одиннадцатиячейник является самодвойственным четырёхмерным многогранником, грани которого не икосаэдры, а «полуикосаэдры». То есть, фигуры, которые получаются, если противоположные стороны икосаэдра считать одной (той же самой) гранью (Grünbaum, 1977). Через несколько лет после открытия Грюнбаумом одиннадцатиячейника Коксетер обнаружил похожий многогранник, пятидесятисемиячейник[англ.] (Coxeter 1982, 1984), а затем, независимо, переоткрыл одиннадцатиячейник.
Эгон Шульте (Egon Schulte) определил «правильные комплексы инциденций» и «правильные инциденциальные многогранники» в свой диссертации в 1980-х, в которой было в первый раз приведено современное определение. Впоследствии он и Питер Макмаллен[англ.] разработали базовую теорию в серии статей, которые позднее собраны в книгу. Многочисленные исследователи внесли с тех пор свою лепту, а пионеры исследований (включая Грюнбаума) приняли определение Шульте в качестве «правильного».
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.