משפט פיתגורס

משפט פיתגורס הוא משפט מפורסם בגאומטריה, המתאר את היחס בין שלוש צלעותיו של משולש ישר-זווית. המשפט קובע כי ”סכום שטחי הריבועים, הבנויים על הניצבים במשולש ישר-זווית, שווה לשטח הריבוע הבנוי על היתר” (הניצבים הם שתי הצלעות שביניהן כלואה הזווית הישרה, והיתר הוא הצלע הארוכה של המשולש). בניסוח פורמלי: אם אורכי הניצבים במשולש ישר-זווית הם ${\displaystyle \ a}$ ו-${\displaystyle \ b}$, ואורך היתר הוא ${\displaystyle \ c}$, אז: ${\displaystyle \ a^{2}+b^{2}=c^{2}}$.

ערך זה עוסק במשפט בגאומטריה. אם התכוונתם למחזה מאת נתן אלתרמן, ראו משפט פיתגורס (מחזה).

בערך זה נעשה שימוש בסימנים מוסכמים מתחום המתמטיקה. להבהרת הסימנים ראו סימון מתמטי.

לוח חרס שמקורו בבבל, המתוארך בין השנים 2003–1595 לפנה"ס. בלוח, הכתוב בכתב יתדות, הוכחה מתמטית הדומה למשפט פיתגורס.

פלימפטון 322 - לוח חרס שמקורו בבבל, המתוארך בין השנים 1822–1784 לפנה"ס. בלוח, הכתוב בכתב יתדות, ארבע עמודות וחמש עשרה שורות של מספרים בספרות בבליות, כך שהמספרים בשתיים מן העמודות שייכים לשלשות פיתגוריות.

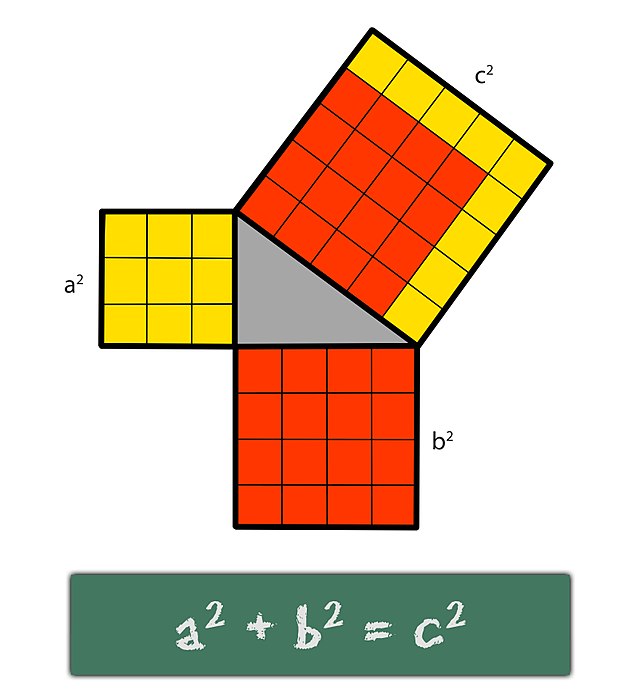
המשפט נקרא על שם המתמטיקאי והפילוסוף היווני פיתגורס, שחי במאה ה-6 לפנה"ס, אשר נהוג לייחס לו את ההוכחה הכללית הראשונה של המשפט, אם כי אין ודאות שהוא אכן זה שהוכיח את המשפט לראשונה. המשפט עצמו ללא ההוכחה היה מוכר מאות שנים לפני זמנו של פיתגורס - במצרים העתיקה, בבבל ובסין, אולם המתמטיקאים היוונים היו הראשונים שעמלו למצוא הוכחות לרעיונות מתמטיים.

המשפט ההפוך, הקובע שמשולש שבו ריבוע צלע אחת שווה לסכום ריבועי הצלעות האחרות הוא ישר-זווית, נכון גם הוא. משפט פיתגורס והמשפט ההפוך לו מופיעים כמשפטים האחרונים בכרך הראשון של "יסודות" - ספרו הנודע של אוקלידס. משפט פיתגורס מהווה מקרה פרטי של משפט הקוסינוסים, המופיע אף הוא ב"יסודות" של אוקלידס, המגדיר את היחס של שלוש צלעותיו של כל משולש, בהינתן אורכן של שתיים מצלעותיו וגודל הזווית הכלואה ביניהן.

בתורת המספרים קיימת בעיה מפורסמת הקשורה למשפט פיתגורס, ובה נדרש למצוא משולשים ישרי זווית שאורכי הצלעות שלהם הם מספרים שלמים, כלומר למצוא פתרונות שלמים למשוואה הדיופנטית: ${\displaystyle \ a^{2}+b^{2}=c^{2}}$. שלשה של מספרים כאלה קרויה שלשה פיתגורית, וידוע שיש אינסוף שלשות מסוג זה. דוגמה לשלשה פיתגורית הם המספרים 3,4,5 שכן הם מקיימים את המשוואה: ${\displaystyle \ (9+16=25)\quad 3^{2}+4^{2}=5^{2}\quad }$.

היסטוריה של משפט פיתגורס

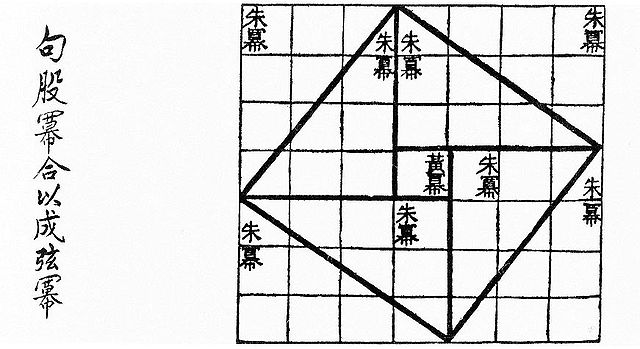
את המשפט עצמו הכירו בתרבויות עתיקות זמן רב לפני פיתגורס^[1]. בקרב חוקרי ההיסטוריה של המתמטיקה אין הסכמה לגבי השאלה האם משפט פיתגורס התגלה פעם אחת, ונדד בין התרבויות השונות בעת העתיקה, או שמא התגלה בכמה מקומות באופן עצמאי ובלתי תלוי.

המתמטיקאי ההולנדי ברטל לינדרט ואן-דר-ורדן סבר כי המשפט התגלה בבריטניה הנאוליתית^[2], וממנה הופץ למצרים ולמסופוטמיה. בהמשך הועבר הידע להודו, לסין וליוון. השערה זו מבוססת על גילויים של מבנים פרהיסטוריים באיים הבריטים, הבנויים בזוויות ישרות וצלעות שהיחסים בין אורכיהן הם מספרים שלמים. מבנים אלו מתוארכים למאה ה-25 לפנה"ס.

משפט פיתגורס בתרבויות קדומות

• מצרים העתיקה

בפפירוס ברלין 6619, המתוארך לתקופה שבין 2000 לפנה"ס ל-1780 לפנה"ס, והמכיל ידע רב במתמטיקה וברפואה, מצויה בעיה^[3] שפתרונה מעיד על ידע בפתרון משוואה ממעלה שנייה ועל הכרתן של מספר שלשות פיתגוריות.

• בבל

לוח החרסית הכתוב בכתב יתדות, "פלימפטון 322", המתוארך לתקופה שבין 1900 לפנה"ס ל-1600 לפנה"ס, מכיל ארבע עמודות וחמש עשרה שורות של מספרים בספרות בבליות. לפי אחת הפרשנויות, הלוח שימש לחישוב שלשות פיתגוריות או לחישוב ערכיה של פונקציה טריגונומטרית^[4].

• הודו

ספר הקודש ההודי, "שולבה סוטרא"^[5], המתאר בניית מזבחות המיועדים להקרבת קורבנות, אשר מתוארך לתקופה שבין 800 לפנה"ס ל-200 לפנה"ס, מכיל רשימה של שלשות פיתגוריות והוכחה גאומטרית של המשפט עבור משולש ישר-זווית שווה-שוקיים.

הוכחה ויזואלית למשפט פיתגורס למשולש (5, 4, 3) כפי שמופיעה בספר "ג'וֹאוּבִּי סְוָּאנְגִ'ינְג", סין

• סין^[6]

בספר "ג'וֹאוּבִּי סְוָּאנְגִ'ינְג" - "המדריך של ג'ואו למדידת צללים" - המתוארך לתקופה שבין 100 לפנה"ס ל-100 לספירה מצויה הוכחה ויזואלית למשפט פיתגורס ("משפט גאוגו" בשמו הסיני) למשולש ישר-זווית שאורכי צלעותיו הן 3, 4 ו-5.

הספר, הנחשב לחשוב ביותר בהיסטוריה של המתמטיקה בסין, הוא "גְ'יו גָא'נְג סוָּאן שוּ" - "תשעת הפרקים של אמנות המתמטיקה", מכיל 246 בעיות מתחומי חיים שונים האמורות להקיף את הידע הדרוש לפתרון בעיות מתמטיות יום-יומיות. הפרק התשיעי של הספר, ששמו "גוּאַי גוּ" ("בסיס וגובה"), עוסק במשולשים ישרי זווית וכולל יישומים של מה שידוע במערב כמשפט פיתגורס, שלשות פיתגוריות וחפיפת משולשים.

משולש ישר-זווית שאורך הניצבים שלו הוא 1

• יוון

במאה השלישית לפנה"ס נכתב בידי אוקלידס הספר "יסודות", המכיל סיכום מקיף של הידע בגאומטריה ובאריתמטיקה שנצבר עד זמנו. תרומתו הגדולה הייתה בניסוח השיטתי ובמבנה הלוגי המסודר של המשפטים. הספר נחשב לאחד הספרים החשובים ביותר שנכתבו מאז ומעולם, והיה הספר המרכזי ללימוד אריתמטיקה וגאומטריה במשך מאות שנים.

בספר מצויה הוכחה למשפט פיתגורס^[7] (ראו בהמשך). ההוכחה כתובה בצורה אקסיומטית ומובנית, והיא ההוכחה העתיקה ביותר למשפט הידועה היום.

לפי הפילוסוף והמתמטיקאי פרוקולוס, שפירש את "יסודות" של אוקלידס כ-700 שנים לאחר כתיבתו, השתמש פיתגורס, שחי במאה השישית לפנה"ס, בשיטות אלגבריות למציאת שלשות פיתגוריות, ואילו אפלטון, שחי בתחילת המאה הרביעית לפנה"ס, פיתח שיטה למציאת שלשות פיתגוריות המשלבת בין האלגברה לגאומטריה.

על-פי משפט פיתגורס, השורש הריבועי של 2 (הידוע גם כקבוע פיתגורס) הוא אורך האלכסון בריבוע שאורך צלעותיו הוא 1. פיתגורס ותלמידיו ידעו להוכיח ש-${\displaystyle {\sqrt {2}}}$ הוא מספר אי רציונלי, מה שלפי סברה רווחת היווה מכה קשה לאסכולה הפיתגוראית שהאמינה שהעולם כולו ניתן לתיאור כיחסים בין מספרים טבעיים.

הוכחות מפורסמות

למשפט פיתגורס התפרסמו הוכחות רבות. ייתכן אף שמשפט פיתגורס הוא המשפט המתמטי בעל המספר הגדול ביותר של הוכחות (ראו בהמשך קישור ל-367 הוכחות). עם האנשים שמצאו הוכחות חדשות למשפט נמנים לאונרדו דה וינצ'י, הנשיא ה-20 של ארצות הברית, ג'יימס גרפילד, ואלברט איינשטיין (בנעוריו).^[8]

אוקלידס

בספרו הנודע של אוקלידס, "יסודות", כרך ראשון, משפט מספר 47, מצויה ההוכחה הבאה למשפט:

יהי ABC משולש ישר-זווית, כאשר C היא הזווית הישרה. מנקודה C מעבירים גובה ליתר, כך שיחצה את הריבוע המונח עליו לשני מלבנים. ההוכחה מראה ששטחי המלבנים האלו שווים לשטחים של הריבועים המונחים על הניצבים בהתאמה. כפי שניתן לראות בציור משמאל, ההוכחה מבוססת על המרת כל אחד משני הריבועים המונחים על הניצבים למקבילית בעלת אותו שטח, השווה גם לשטחו של המלבן המתאים.

להלן פרטי ההוכחה^[9]:

1. ABC הוא משולש ישר-זווית, עם זווית ישרה ACB.
2. על כל אחת מצלעות המשולש AB, BC, CA מונחים הריבועים ABIK, BCFG, CADE בהתאמה.
3. הגובה מקודקוד C ליתר AB חותך את הצלעות AB, KI בנקודות H, J בהתאמה.
4. הזוויות ACB ו-ACE הן זוויות ישרות ולכן הנקודות B, C ,E נמצאות על ישר אחד. כנ"ל לגבי הנקודות A, C, F.
5. הזוויות DAC ו-BAK הן זוויות ישרות, לכן המשולשים KAC ו-BAD חופפים (AD=AC, הזוויות KAC ו-BAD שוות, BA=KA).
6. מאחר שהנקודות C, H, J נמצאות על ישר אחד, אזי שטח המלבן KAHJ שווה לפעמיים שטח המשולש KAC^[10].
7. מאחר שהנקודות B, C, E נמצאות על ישר אחד, אזי שטח הריבוע ADEC שווה לפעמיים שטח המשולש ADB.
8. מכאן ששטח המלבן KAHJ שווה לשטח הריבוע ADEC, כלומר שטח המלבן KAHJ שווה ל-AC^2.
9. משימוש באותם השיקולים מתקבל ששטח המלבן IBHJ שווה ל-BC^2.
10. מחיבור שתי תוצאות אלו נובע ששטח הריבוע IBAK שווה ל-AC²+BC^2.
11. מחישוב ישיר של שטח הריבוע IBAK, שטחו שווה ל-AB^2.
12. סך הכל, מקבלים כי: AC²+BC²=AB^2.

הוכחה נוספת של אוקלידס

נשרטט אנך מקודקוד הזווית הישרה ליתר, ונקבל שני משולשים קטנים. הזוויות בשני המשולשים הקטנים שוות לזוויות במשולש המקורי, ולכן שלושת המשולשים דומים.

כתוצאה מדמיון המשולשים היתר חלקי הניצב במשולש העליון, שווה ליתר חלקי הניצב התואם במשולש הגדול:

${\displaystyle c \over a}$=${\displaystyle a \over c1}$

מכאן ${\displaystyle a^{2}=c*c1}$

באופן דומה במשולש התחתון:

${\displaystyle c \over b}$=${\displaystyle b \over c2}$

מכאן ${\displaystyle b^{2}=c*c2}$

נחבר את שתי המשוואות:

${\displaystyle a^{2}+b^{2}=c*c1+c*c2=c*(c1+c2)=c^{2}}$

${\displaystyle a^{2}+b^{2}=c^{2}}$

לאונרדו דה וינצ'י

הוכחתו של דה וינצ'י למשפט פיתגורס

הסבר להוכחתו של לאונרדו דה וינצ'י, המתוארת בסקיצה משמאל:

המרובעים האפורים AJIC ו-ABGD חופפים ולכן שטחם שווה. כך גם המרובעים הלבנים DGFE ו-CIHB. מתקבל כי שטח המשושים AJIHBC ו-ABGFED שווה.

שטח המשושה AJIHBC שווה ל- ${\displaystyle c^{2}+2\cdot {\frac {ab}{2}}=c^{2}+ab}$

שטח המשושה ABGFED שווה ל- ${\displaystyle a^{2}+b^{2}+2\cdot {\frac {ab}{2}}=a^{2}+b^{2}+ab}$

מהשוואת שני הביטויים שהתקבלו, המייצגים את אותו שטח, מתקבל משפט פיתגורס.

הנשיא גרפילד

הוכחת הנשיא גרפילד למשפט פיתגורס

ג'יימס גרפילד, שכיהן כנשיא ארצות הברית במחצית השנייה של המאה ה-19, חיבר בשנת 1876 (טרם בחירתו לנשיא) הוכחה יפה למשפט פיתגורס, המבוססת על הנחת שני עותקים של המשולש ישר-הזווית לאורכו של קו ישר כמודגם בציור משמאל. מתקבל טרפז, שאת שטחו ניתן לחשב בשני אופנים:

מצד אחד, שטחו שווה ל-${\displaystyle \ {\frac {(a+b)^{2}}{2}}}$, כיוון ששטח טרפז שווה למכפלת גובהו במחצית סכום בסיסיו.

מצד שני, שטחו שווה ל-${\displaystyle \ {\frac {c^{2}}{2}}+ab}$ כי הוא שווה לסכום שטחם של שני המשולשים האפורים והמשולש הלבן שביניהם.

מהשוואת שני הביטויים, המייצגים את אותו שטח, מתקבל משפט פיתגורס.

שיטות הוכחה נוספות

כאמור, למשפט פיתגורס התפרסמו עשרות רבות של הוכחות המבוססות על שיטות שונות. רובן הגדול של ההוכחות מבוסס על גאומטריה: חישוב של אותו שטח בשתי דרכים שונות, בחלקן תוך סידור מחדש של השטח; שימוש במשולשים דומים ובמשולשים חופפים; שימוש בקווים מיוחדים במעגל: רדיוס ומשיק.

הוכחות פחות שגרתיות מתבססות על כלים מתמטיים מתקדמים יותר, כמו חשבון דיפרנציאלי ואנליזה ממדית.

השוואת שטחים

דרך אחת להוכחת המשפט היא חישוב שטח של צורה נתונה בשתי דרכים שונות, שההשוואה ביניהן נותנת את משפט פיתגורס. דוגמה להוכחה בדרך זו, היא הוכחתו של הנשיא גרפילד שהוצגה לעיל.

וריאציה אחרת של שיטה זו, היא חישוב שטח של צורה מסוימת, סידור מחדש של השטח על ידי חיתוך והרכבה, חישוב מחדש של השטח, וכמו קודם, מהשוואת השטחים מתקבל משפט פיתגורס. דוגמה להוכחה בשיטה זו, היא הוכחתו של לאונרדו דה וינצ'י. דוגמאות נוספות לגישה זו, בהנפשות הבאות:

הכללה של ההוכחה המופיעה בטקסט הסיני "Chou Pei Suan Ching" עבור המשולש (3,4,5) למשולש כללי

הוכחתו של המתמטיקאי ההודי אריאבהטה שחי במאה ה-5 לספירה

חפיפה ודמיון משולשים

הוכחה באמצעות דמיון משולשים

אחת הדרכים הנפוצות להוכחת המשפט היא שימוש בחפיפת משולשים, כמו בהוכחתו של אוקלידס, או שימוש בדמיון משולשים, כמו בדוגמה הבאה:

נתון משולש ישר-זווית ABC, כאשר ${\displaystyle \angle ACB}$ היא הזווית הישרה.

מהקודקוד C מורידים גובה לצלע AB ומקבלים שלושה משולשים דומים: ACB, ADC, CDB.

את המשך ההוכחה ניתן לראות בציור משמאל.

פרשנים טוענים שההוכחה הייתה ידועה לאוקלידס כאשר כתב את "יסודות", אך כיוון שרצה לכלול את משפט פיתגורס כבר בכרך הראשון של ספריו, לפני המשפטים שעוסקים בדמיון משולשים, הוא השתמש בהוכחה מורכבת יותר.

קווים מיוחדים במעגל

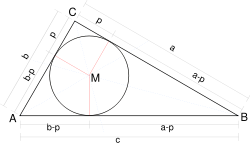
בשימוש בתכונותיהם של הרדיוס והמשיק למעגל, כמו בדוגמה הבאה: מעגל בעל רדיוס ${\displaystyle \rho \,}$ חסום במשולש ABC. שטח המשולש שווה לסכום שטחי המשולשים הצבעוניים: ${\displaystyle {\rho \cdot {\tfrac {a}{2}}}+{\rho \cdot {\tfrac {b}{2}}}+{\rho \cdot {\tfrac {c}{2}}}}$ . מהשוואת נוסחה זו לנוסחה הרגילה לחישוב שטח משולש ${\displaystyle {\tfrac {ab}{2}}\,}$ מתקבל: ${\displaystyle \rho ={\tfrac {ab}{a+b+c}}}$. אורך הצלע c שווה ל ${\displaystyle (a-\rho )+(b-\rho )}$. לאחר העברת אגפים מתקבל: ${\displaystyle \rho ={\tfrac {a+b-c}{2}}}$ מהשוואת שני הביטויים שהתקבלו המייצגים את ${\displaystyle \rho \,}$ מתקבל משפט פיתגורס.

שימוש בחשבון דיפרנציאלי

הוכחת המשפט באמצעות משוואות דיפרנציאליות.

בגישה זו, אורך אחד הניצבים ${\displaystyle b}$ הוא קבוע ובודקים כיצד משתנה אורך היתר ${\displaystyle c}$ בהתאם לשינוי באורך הניצב השני ${\displaystyle a}$, כפי שניתן לראות בדיאגרמה משמאל.

באמצעות דמיון משולשים מקבלים את המשוואה: ${\displaystyle {\frac {da}{dc}}={\frac {c}{a}}}$.

ואחרי העברת אגפים, מתקבלת המשוואה הדיפרנציאלית: ${\displaystyle c\,dc=a\,da}$.

התרתה של משוואה זו (באמצעות אינטגרציה של שני האגפים) מביאה לפתרון: ${\displaystyle c^{2}=a^{2}+\mathrm {constant} \ \,\!}$.

מכיוון שעבור המקרה שבו ${\displaystyle a=0\,}$ מתקבל כי ${\displaystyle c=b\,}$, אזי הקבוע בפתרון הוא בדיוק ${\displaystyle b^{2}\,}$.
הצבתו של הקבוע במשוואה מביאה לתוצאה הדרושה: ${\displaystyle c^{2}=a^{2}+b^{2}\,}$.

שימוש באנליזה ממדית

הוכחת משפט פיתגורס באמצעות אנליזה ממדית

את משפט פיתגורס ניתן להוכיח גם משיקולים של אנליזה ממדית. זוויות המשולש הן חסרות ממד; אורכיהן של צלעות המשולש הן מממד L; שטח המשולש הוא מממד L². את שטח המשולש ניתן להביע כפונקציה של היתר ושל אחת מהזוויות החדות במשולש שתסומן באות היוונית ${\displaystyle \ \alpha }$. מכיוון ש-${\displaystyle \ \alpha }$ חסר ממד, c מממד L והשטח מממד L² הרי ששטח המשולש ABC שווה ל- ${\displaystyle Area_{ABC}=c^{2}f(\alpha )\,}$. הגובה מקודקוד C פוגש את הצלע AB בנקודה D. מאותם שיקולי ממד מקבלים ששטח המשולש ACD שווה ל- ${\displaystyle Area_{ACD}=b^{2}f(\alpha )\,}$ ואילו שטח המשולש BCD שווה ל- ${\displaystyle Area_{BCD}=a^{2}f(\alpha )\,}$. מכיוון ש-${\displaystyle Area_{ABC}=Area_{BCD}+Area_{ACD}}$ הרי ש-${\displaystyle c^{2}f(\alpha )=a^{2}f(\alpha )+b^{2}f(\alpha )\,}$. לאחר צמצום בגורם ${\displaystyle f(\alpha )\,}$ ששונה מ 0 מתקבל משפט פיתגורס.

המשפט ההפוך

המשפט ההפוך למשפט פיתגורס נכון גם הוא:

כל משולש שצלעותיו ${\displaystyle \ a,b,c}$ מקיימות את המשוואה a² + b² = c², הוא משולש ישר-זווית.

משפט זה מופיע גם כן בכרך הראשון של ה"יסודות" של אוקלידס, כמשפט 48.

ניתן להוכיח את המשפט באמצעות משפט הקוסינוסים (ראו גם בהמשך תחת הכללות), או באמצעות משפט פיתגורס עצמו, באופן הבא:

יהי ABC משולש שצלעותיו ${\displaystyle \ a,b,c}$ מקיימות את המשוואה a² + b² = c² כדי להוכיח שהזווית בין הצלעות a ו-b היא זווית ישרה, בונים משולש ישר-זווית שארכי ניצביו הם a ו-b. לפי משפט פיתגורס, אורך היתר במשולש החדש הוא c. מכיוון שאורכי הצלעות במשולש המקורי שווים לאורכי הצלעות במשולש החדש, נובע בהכרח שהמשולשים חופפים ולכן גם הזוויות שלהן שוות. לכן, המשולש המקורי הוא בהכרח ישר-זווית.

הכללתו של המשפט ההפוך, נותנת כלי פשוט לקביעה האם משולש שצלעותיו ${\displaystyle a,b,c\,}$, כאשר c הצלע הארוכה ביניהן, הוא חד-זווית, ישר-זווית או קהה-זווית:

• אם a² + b² = c² אז המשולש הנתון הוא ישר-זווית.
• אם a² + b² > c² אז המשולש הנתון הוא חד זווית.
• אם a² + b² < c² אז המשולש הנתון הוא קהה זווית.

בניסוח קומפקטי, שנוסח על ידי אדסחר דייקסטרה^[11], המבוסס על פונקציית הסימן: ${\displaystyle \ \operatorname {sgn}(\alpha +\beta -\gamma )=\operatorname {sgn}(a^{2}+b^{2}-c^{2})}$.

שימושים

שימושים יומיומיים במשפט פיתגורס יושמו עוד לפני שפיתגורס ניסח אותו.

הוכחה גאומטרית לאי שוויון הממוצעים עבור שני מספרים a>b>0 המשתמשת במשפט פיתגורס.${\displaystyle RMS={\sqrt {\tfrac {a^{2}+b^{2}}{2}}}}$, ${\displaystyle AM={\tfrac {a+b}{2}}}$, ${\displaystyle GM={\sqrt {ab}}}$, ${\displaystyle HM={\tfrac {2}{{\tfrac {1}{a}}+{\tfrac {1}{b}}}}}$

הוכחות גאומטריות למשפטים מתמטיים שונים

משפט פיתגורס משמש בהוכחת משפטים רבים מתחום הגאומטריה, למשל נוסחת הירון או המשפט ההפוך למשפט פיתגורס.
בטריגונומטריה, משפט פיתגורס מהווה כלי חשוב בהוכחתן של זהויות. למשל: במשולש ישר-זווית שאורך היתר שלו הוא 1, ואחת מזוויותיו החדות היא x, אורכי הניצבים הם ${\displaystyle \sin x,\cos x\,}$. ממשפט פיתגורס מקבלים את הזהות ${\displaystyle {\sin }^{2}x+{\cos }^{2}x=1\,}$.
כמו כן, ניתן להשתמש במשפט פיתגורס כדי לתת הוכחה גאומטרית למשפטים מתחומים אחרים במתמטיקה, כמו המקרה ${\displaystyle \ n=2}$ של אי שוויון הממוצעים.

מרחק במרחב האוקלידי

במרחב האוקלידי מגדירים את המרחק במערכת הקואורדינטות הקרטזיות באמצעות משפט פיתגורס:

בהינתן שתי נקודות (x₁, y₁), (x₀, y₀) ב-${\displaystyle \mathbb {R} ^{2}}$, המרחק האוקלידי ביניהן נתון על ידי הנוסחה: ${\displaystyle d={\sqrt {(x_{1}-x_{0})^{2}+(y_{1}-y_{0})^{2}}}}$

את הנוסחה הנ"ל ניתן להרחיב גם למרחב האוקלידי ה-n ממדי באופן הבא:

בהינתן הנקודות ${\displaystyle \scriptstyle X\,=\,(x_{1},x_{2},\dots ,x_{n})}$, ${\displaystyle \scriptstyle Y\,=\,(y_{1},y_{2},\dots ,y_{n})}$ ב- ${\displaystyle \mathbb {R} ^{n}}$, המרחק האוקלידי ביניהן נתון על ידי הנוסחה: ${\displaystyle d={\sqrt {(x_{1}-y_{1})^{2}+(x_{2}-y_{2})^{2}+\cdots +(x_{n}-y_{n})^{2}}}={\sqrt {\sum _{i=1}^{n}(x_{i}-y_{i})^{2}}}}$

ציוד המרחב האוקלידי בפונקציית מרחק לפי משפט פיתגורס הופכת אותו למרחב מטרי שהמטריקה שלו קרויה "המטריקה האוקלידית".

מושג קרוב למרחק הוא אורך. במרחב האוקלידי הסטנדרטי האורך מוגדר בדומה למרחק לפי משפט פיתגורס. האורך האוקלידי של וקטור ${\displaystyle (x_{1},x_{2},\ldots ,x_{n})}$ הוא ${\displaystyle {\sqrt {x_{1}^{2}+x_{2}^{2}+\ldots +x_{n}^{2}}}}$. זוהי הנורמה הסטנדרטית המושרת על המרחב האוקלידי כמרחב מכפלה פנימית עם מכפלה סקלרית.

הגדרה בסיסית זו של אורך של וקטור (שהוא קו ישר) מאפשר להגדיר אורך של כל עקומה בעלת אורך. האורך של עקומה מתקבל על ידי חלוקת העקומה למקטעים ישרים, שאורך כל אחד מהם קטן מ ${\displaystyle \ \epsilon }$, סכימת האורכים של המקטעים (המחושבים לפי פיתגורס) ולבסוף חישוב הגבול של אורך זה כאשר ערכו של ${\displaystyle \ \epsilon }$ שואף ל-0.

הערך המוחלט של מספר מרוכב מתקבל גם הוא ממשפט פיתגורס. זהו האורך של המספר כווקטור במישור המרוכב.

בניית שורשים של שלמים בעזרת סרגל ומחוגה

בניות בעזרת סרגל ומחוגה של שורשי שלמים.

לכל מספר טבעי n, משפט פיתגורס מאפשר לבנות קטע באורך ${\displaystyle {\sqrt {n}}}$ בעזרת סרגל ומחוגה. כדי לבנות את ${\displaystyle {\sqrt {2}}}$ בונים את היתר של משולש ישר-זווית עם ניצבים באורך 1. כדי לבנות ${\displaystyle {\sqrt {3}}}$ בונים את היתר של משולש יש זווית עם ניצב באורך 1 וניצב באורך ${\displaystyle {\sqrt {2}}}$ וכן הלאה.

באופן כללי, נבנה את השורש של n באינדוקציה. בהינתן שבנינו כבר את ${\displaystyle {\sqrt {n-1}}}$, אז נבנה משולש ישר-זווית עם ניצב באורך זה וניצב באורך 1, ולפי משפט פיתגורס נקבל יתר שאורכו: ${\displaystyle {\sqrt {({\sqrt {n-1}})^{2}+1^{2}}}={\sqrt {n}}}$.

בנייה זו מעידה שהשורשים הריבועיים של המספרים הטבעיים נמצאים בשדה המספרים הניתנים לבנייה.

חישוב ערכים של הפונקציות הטריגונומטריות

משולש 90°-60°-30°

משפט פיתגורס מאפשר למצוא ערכים פשוטים של פונקציות טריגונומטריות.

הערכים של קוסינוס וסינוס (ולכן גם טנגנס) בזוויות 30°,45°,60° מתקבלים ממשפט פיתגורס בקלות.

כדי למצוא את ערכי הפונקציות בזווית 45° בונים משולש ישר-זווית שהוא גם שווה-שוקיים. לשם הפשטות קובעים כי אורכי הניצבים הם 1. זוויות הבסיס במשולש שוות ולכן הן 45° (כי סכום הזוויות במשולש הוא 180°). לפי משפט פיתגורס אורך היתר הוא ${\displaystyle {\sqrt {2}}}$, ולכן מהגדרת הפונקציות הטריגונומטריות במשולש נובע ש-${\displaystyle \cos 45^{\circ }=\sin 45^{\circ }={\tfrac {1}{\sqrt {2}}}}$

כדי למצוא את ערכי הפונקציה בזוויות 30° ו-60° מתחילים ממשולש שווה-צלעות שכל צלעותיו הן באורך 2. מכיוון שהמשולש שווה-צלעות כל זוויותיו הן בנות 60°. כעת מורידים גובה מאחד הקודקודים. הגובה הוא גם חוצה זווית ולכן מתקבל משולש שזוויותיו הן 90°-60°-30°. הגובה הוא גם תיכון ולכן למשולש שהתקבל ניצב באורך 1 (מול הזווית 30°) ויתר באורך 2. לפי משפט פיתגורס אורך הניצב השני (מול הזווית 60°) הוא ${\displaystyle {\sqrt {2^{2}-1^{2}}}={\sqrt {3}}}$. לכן מקבלים ש-${\displaystyle \sin 30^{\circ }=\cos 60^{\circ }={\tfrac {1}{2}}}$ וכן ${\displaystyle \cos 30^{\circ }=\sin 60^{\circ }={\tfrac {\sqrt {3}}{2}}}$.

הכללות

למשפט פיתגורס ישנן הכללות רבות, חלקן היו ידועות עוד בימי קדם. הכללות חדשות ממשיכות להתגלות, כאשר מתמטיקאים בוחנים את ההוכחות השונות של המשפט ומנסים להכלילן. הכללות אלו ניתן לסווג בשלוש קטגוריות:

• הכללות של המשפט למשולש כלשהו, (לאו דווקא ישר-זווית) ולמצולעים שונים (לאו דווקא משולש).
• משפטים דומים, בהם על צלעות המשולש בונים צורה גאומטרית כלשהי, (לאו דווקא ריבוע).
• הכללות לגאומטריה אוקלידית מממדים גבוהים יותר (לאו דווקא גאומטריה מישורית).

הכללות למשולש כלשהו ולמצולעים שונים

משפט הקוסינוסים

ערך מורחב – משפט הקוסינוסים

משפט הקוסינוסים במשולש חד-זווית

ההכללה הידועה ביותר של משפט פיתגורס למשולש כללי היא משפט הקוסינוסים. בגרסתו המוכרת, ניסוחו של משפט הקוסינוסים הוא: ${\displaystyle a^{2}+b^{2}-2ab\cos {\gamma }=c^{2}\,}$ כאשר ${\displaystyle \gamma \,}$ היא הזווית מול ${\displaystyle c\,}$ .
כאשר ${\displaystyle \gamma }$ היא זווית ישרה, מתקבל משפט פיתגורס (כי ${\displaystyle \cos(90^{\circ })=0\,}$)

למשפט גרסה מוקדמת יותר, המופיעה גם היא ב"יסודות" של אוקלידס ואינה כוללת פונקציות טריגונומטריות:

על כל אחת מהצלעות AB, BC, CA של משולש ABC מונחים ריבועים ABOM, BCIG, CAJL בהתאמה. מכל קודקוד מועבר גובה לצלע ממול החותך גם את הריבוע המונח על צלע זו. אזי מתקיימים השוויונות הבאים:

${\displaystyle AREA_{DHIC}=AREA_{CLKE}}$, ${\displaystyle AREA_{BONF}=AREA_{BGHD}}$, ${\displaystyle AREA_{AEKJ}=AREA_{AFNM}}$.
ניתן להציג שוויונות אלו במשולש חד זווית גם באופן הבא: ${\displaystyle BC^{2}+AC^{2}=AB^{2}+2AREA_{DHIC}}$.
(מכיוון ש ${\displaystyle AREA_{DHIC}=BC\cdot AC\cos(ACB)}$ מתקבל משפט הקוסינוסים בגרסתו המוכרת)

בגרסה זו ברור יותר הקשר בין משפט הקוסינוסים למשפט פיתגורס: אם הזווית ACB היא זווית ישרה, אז הישר KE מתלכד עם הישר LC ואילו הישר DH מתלכד עם הישר CI, כלומר ${\displaystyle AREA_{DHIC}=0}$ ומתקבל משפט פיתגורס.

משפט התיכון

משפט התיכון במשולש כללי: השטח הירוק ועוד השטח הכחול שווה לשטח האדום

התיכון מהקודקוד A במשולש ABC חוצה את הצלע BC בנקודה D.

משפט התיכון קובע כי ${\displaystyle AB^{2}+AC^{2}=2\cdot (AD^{2}+DB^{2})\,}$.

במקרה הפרטי שבו המשולש הוא שווה-שוקיים :

${\displaystyle AB=AC=c\,}$, ${\displaystyle AD=b\,}$, ${\displaystyle BD=a\,}$

מתקבל משפט פיתגורס.

הכללת אבן קורה

הכללת ת'אבת אבן קורה למשפט פיתגורס

הכללה נוספת למשולש כללי, נתונה במשפט הבא המיוחס למתמטיקאי הערבי ת'אבת אבן קורה בן המאה התשיעית: נתון משולש ABC . מקודקוד A יוצאים שני ישרים החותכים את הצלע BC בנקודות g, h, כך ש ${\displaystyle \angle {BAC}=\angle {BgA}=\angle {ChA}=\alpha }$
(בציור משמאל, דוגמה עבור המקרה הפרטי שבו ${\displaystyle \alpha }$ היא זווית קהה).

אזי ${\displaystyle AB^{2}+AC^{2}=BC\cdot (Bg+Ch)}$.

במקרה הפרטי, שבו הזווית ${\displaystyle \ \alpha }$ היא זווית ישרה, הנקודות g, h מתלכדות, ואז ${\displaystyle Bg+Ch=BC}$ ומתקבל משפט פיתגורס.

משפט היין

ערך מורחב – משפט היין

משפט hoehn משנת 2000

המתמטיקאי האמריקאי לארי היין פרסם בשנת 2000 משפט המכליל את משפט פיתגורס^[12], במשולש שווה-שוקיים:
נתון משולש שווה-שוקיים שאורך השוק שלו הוא c. ישר באורך a המחבר את זווית הראש והבסיס חוצה את הבסיס לשני קטעים שאורכיהם b, d. אזי: ${\displaystyle \quad c^{2}=a^{2}+bd\quad \,}$

במקרה הפרטי שבו הישר הפנימי הוא גובה (ולפי משפט ידוע בגאומטריה, גם תיכון), מתקיים ש ${\displaystyle b=d\,}$ ומתקבל משפט פיתגורס.

לא רק ריבוע

מתוך ה"יסודות" של אוקלידס

הכללה למשפט פיתגורס, ניתן למצוא כבר ב"יסודות" של אוקלידס^[13]:

אם על צלעותיו של משולש ישר-זווית מונחות צורות דומות, אזי סכומם של שני השטחים הקטנים, שווה לשטח הגדול.

בצורה פורמלית יותר: אם על צלעות משולש ישר-זווית שאורכי צלעותיו הן ${\displaystyle a,b,c\,}$ בונים צורות ששטחיהן A,B,C כך ש ${\displaystyle {\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}}$, אזי ${\displaystyle A+B=C}$.

משפט תלמי

מקרה פרטי של משפט תלמי בו המרובע החסום במעגל הוא מלבן.

משפט תלמי בגאומטריה קובע שאם מרובע ABCD הוא ציקלי, כלומר ניתן לחסום אותו במעגל,

כלומר: ${\displaystyle \angle A+\angle C=\angle B+\angle D}$,

אז ${\displaystyle AB\cdot CD+AD\cdot BC=AC\cdot BD\quad }$.

במקרה הפרטי שבו המרובע הנדון הוא מלבן שאורכי צלעותיו ואלכסוניו הם:
${\displaystyle AD=BC=a\,}$, ${\displaystyle AB=CD=b\,}$ , ${\displaystyle AC=BD=c\,}$,
מתקבל משפט פיתגורס.

מקביליות הבנויות על צלעות משולש כללי

השטח האדום ועוד השטח הכחול שווה לשטח הירוק

על הצלעות AC ו-BC של משולש ABC, בונים מקביליות ACED ו-BCGF בהתאמה.

הקרנות DE ו-FG נחתכות בנקודה H.
על הצלע AB בונים מקבילית ABJI שצלעותיה AI, BJ, מקבילות לקטע CH ושוות לו באורכן.

אזי ${\displaystyle AREA_{ACED}+AREA_{BCGF}=AREA_{ABJI}}$. הוכחה זו מופיעה בספר הרביעי בסדרת האסיף המתמטי של פאפוס מאלכסנדריה.

במקרה הפרטי, בו המשולש הוא ישר-זווית, והמקביליות הן ריבועים, מתקבל משפט פיתגורס.

הכללת ויליאם האזרד

השטח האדום שווה לשטח הכחול

המתמטיקאי האמריקאי ויליאם האזארד פרסם בשנת 1929 הכללה^[14] להוכחתו של המתמטיקאי ההודי אריאבהטה למשפט פיתגורס.

בנייה:

המקבילית ABCD חסומה במקבילית PNMQ, כלומר על כל אחת מצלעות המקבילית PNMQ מונח קודקוד של המקבילית ABCD.

מקודקוד A מעבירים ישר מקביל לקטעים MN, QP החותך את הצלע QM בנקודה S.

מקודקוד B מעבירים ישר מקביל לקטעים MQ, NP החותך את הצלע PQ בנקודה K.

הישרים AS, BK נחתכים בנקודה Y.

אזי: ${\displaystyle Area_{ABCD}=Area_{AYKP}+Area_{BYSM}\,}$.

כאשר שתי המקביליות הן ריבועים, מתקבל משפט פיתגורס (כמו בהוכחתו של אריאבהטה).

גאומטריה מסדר גבוה יותר ומרחבים נורמיים

משפט דה גוּאַה

משפט דה גואה, על שמו של המתמטיקאי הצרפתי ז'אן דה-גואה דה-מלבס, הוא הכללה של משפט פיתגורס לשלושה ממדים. המשפט קובע שאם לפירמידה משולשת יש פינה ישרה, כלומר: ${\displaystyle \angle {A_{1}A_{4}A_{2}}=\angle {A_{1}A_{4}A_{3}}=\angle {A_{3}A_{4}A_{2}}=90^{0}}$, אז סכום ריבועי השטחים של הפאות היוצרות את הפינה הישרה, שווה לריבוע הפאה הרביעית, כלומר:

${\displaystyle AREA_{A_{1}A_{4}A_{2}}^{2}+AREA_{A_{1}A_{4}A_{3}}^{2}+AREA_{A_{3}A_{4}A_{2}}^{2}=AREA_{A_{1}A_{2}A_{3}}^{2}}$

משפט אנלוגי קיים גם בממד רביעי ומעלה.

משפט פיתגורס במרחב מכפלה פנימית

אם u ו-v הם וקטורים אורתוגונליים (מאונכים) במרחב מכפלה פנימית, אזי ${\displaystyle \|{\vec {v}}+{\vec {w}}\|^{2}=\|{\vec {v}}\|^{2}+\|{\vec {w}}\|^{2}}$
באמצעות אינדוקציה מתמטית, ניתן להרחיב את הכלל למספר סופי כלשהו של וקטורים, כך שכל שניים מהם מאונכים זה לזה:

יהיו v₁, v₂,…, v_n וקטורים במרחב מכפלה פנימית כך ש ${\displaystyle \langle v_{i},v_{j}\rangle =0\quad }$ לכל i<j, אזי: ${\displaystyle \left\|\,\sum _{k=1}^{n}\mathbf {v} _{k}\,\right\|^{2}=\sum _{k=1}^{n}\|\mathbf {v} _{k}\|^{2}}$

משפט פיתגורס בגאומטריה לא אוקלידית

הגאומטריה האוקלידית מבוססת על מספר אקסיומות (שנוסחו תחילה על ידי אוקלידס ותוקנו בהמשך על ידי דויד הילברט), בהן אקסיומת המקבילים, לפיה בהינתן ישר ${\displaystyle l}$ ונקודה P שאיננה על הישר, ניתן להעביר דרך P ישר אחד בלבד המקביל ל- ${\displaystyle l}$.

משפט פיתגורס נובע מהאקסיומות של הגאומטריה האוקלידית. למעשה, בגאומטריה האוקלידית, משפט פיתגורס שקול לאקסיומת המקבילים^[15], כלומר: בהינתן האקסיומות של הגאומטריה האוקלידית ללא אקסיומת המקבילים ובתוספת משפט פיתגורס, ניתן להוכיח את אקסיומת המקבילים, ומכאן, גם את כל שאר המשפטים של הגאומטריה האוקלידית.

משפט פיתגורס, בניסוחו המוכר, לא תקף בגאומטריות שאינן אוקלידיות, אך יש לו גרסאות שמותאמות לגאומטריות אלו.

משפט פיתגורס בגאומטריה הספירית

משולש ישר-זווית בגאומטריה ספירית

בגאומטריה הספירית אקסיומת המקבילים מוחלפת באקסיומה הבאה:

בהינתן ישר ${\displaystyle l}$ ונקודה P שאיננה על הישר, לא ניתן להעביר דרך P אף ישר המקביל ל- ${\displaystyle l}$.
בגאומטריה הספירית, המשולשים (וכל שאר העצמים המתמטיים) נמצאים על פני ספירה. כאשר רדיוס הספירה שווה ל-R, ניתן לנסח את משפט פיתגורס באופן הבא:

${\displaystyle \cos \left({\frac {c}{R}}\right)=\cos \left({\frac {a}{R}}\right)\,\cos \left({\frac {b}{R}}\right)}$.

כדי להבין מדוע משפט זה אכן מהווה את המקבילה של משפט פיתגורס, מפתחים את הפונקציה ${\displaystyle \cos {\alpha }\,}$ לטור מקלורן:

${\displaystyle \cos \alpha =1-{\frac {\alpha ^{2}}{2}}+...}$

כאשר מציבים את הפיתוח הנ"ל ב"משפט פיתגורס בגאומטריה הספירית", מקבלים:

${\displaystyle \left(1-{\frac {c^{2}}{2R^{2}}}+...\right)=\left(1-{\frac {a^{2}}{2R^{2}}}+...\right)\cdot \left(1-{\frac {b^{2}}{2R^{2}}}+...\right)}$.

לאחר פתיחת סוגריים, והכפלה בגורם ${\displaystyle 2R^{2}\,}$, מקבלים את משפט פיתגורס בגרסתו האוקלידית כאשר מאפשרים לרדיוס הכדור לשאוף לאינסוף (${\displaystyle \,R\to \infty }$):

${\displaystyle a^{2}+b^{2}=c^{2}\,}$.

משפט פיתגורס בגאומטריה ההיפרבולית

בגאומטריה ההיפרבולית, את אקסיומת המקבילים מחליפה האקסיומה: בהינתן ישר ${\displaystyle l}$ ונקודה P שאיננה על הישר, ניתן להעביר דרך P לפחות שני ישרים המקבילים ל- ${\displaystyle l}$.
במישור היפרבולי בעל עקמומיות 1-, ניתן לנסח את משפט פיתגורס באופן הבא: ${\displaystyle \cosh c=\cosh a\cdot \cosh b}$ כאשר cosh הוא הקוסינוס ההיפרבולי.

גם כאן, על ידי שימוש בטור מקלורן, כאשר ${\displaystyle \,a,b,c\to 0}$ מקבלים את משפט פיתגורס בגרסתו האוקלידית.

בתרבות

• בדיאלוג הסוקרטי "מנון", שכתב הפילוסוף היווני אפלטון שחי בין תקופתו של פיתגורס לזו של אוקלידס, מוצגת הבעיה של בניית ריבוע כפול בשטחו מריבוע נתון. הפתרון הוא למעשה הוכחה למקרה הפרטי של משפט פיתגורס למשולש ישר-זווית ושווה-שוקיים^[16].
• תחום עניין מעט יוצא דופן בפועלו של קרל פרידריך גאוס, היה חקר האפשרות של קיום חיים מחוץ לכדור הארץ. גאוס העלה רעיון לזרוע במדבר סהרה שטח מוריק בן מאות קמ"ר בצורת תרשים של משפט פיתגורס. אם יבחינו החוצנים בטלסקופים שלהם בצורה הזאת, הם יבינו כי הסבירות שהיא מקרית נמוכה ביותר ויסיקו שיצרה אותה ציוויליזציה מתקדמת.
• משפט פיתגורס זוכה לאזכורים רבים בסדרות טלוויזיה ובסרטי קולנוע.
• בסרט "הקוסם מארץ עוץ", כאשר הדחליל מקבל מוח מהקוסם, הדבר הראשון שהוא עושה הוא לצטט את משפט פיתגורס. הוא מצטט את המשפט עם שגיאות מרובות, אך המסר ברור: מי שיודע את משפט פיתגורס לא יכול להיות חסר מוח (סצנה זו אינה קיימת בספר).

ראו גם

• המשפט האחרון של פרמה
• עץ פיתגורס
• שלשה פיתגורית
• פסגת פיתגורס - הר בהרי טולה בארץ אנדרבי שבאנטארקטיקה, הקרוי על שם המשפט.
• פאפוס מאלכסנדריה

לקריאה נוספת

• רוברט פ' קריז, המשוואות הגדולות - פריצות דרך במדע מפיתגורס עד הייזנברג, כתר ספרים, 2008, עמ' 17–43.

• Eli Maor, The Pythagorean Theorem: A 4,000-Year History, Princeton University Press, 2007

קישורים חיצוניים

מיזמי קרן ויקימדיה
ערך מילוני בוויקימילון: משפט פיתגורס
ספר לימוד בוויקיספר: משפט פיתגורס
תמונות ומדיה בוויקישיתוף: משפט פיתגורס

• משפט פיתגורס, דף שער בספרייה הלאומית

• אתר המכיל מעל ל-70 הוכחות שונות והכללות למשפט פיתגורס
• אתר המכיל הוכחות למשפט פיתגורס ומספר הכללות
• הוכחות אינטראקטיביות למשפט פיתגורס:
  • ההוכחה של אוקלידס
  • ההוכחה המופיעה בטקסט הסיני "Chou Pei Suan Ching"
• Elisha Scott Loomis, The Pythagorean Proposition - ‏ 367 הוכחות למשפט פיתגורס
• משפט פיתגורס, באתר MathWorld (באנגלית)
• משפט פיתגורס, באתר אנציקלופדיה בריטניקה (באנגלית)

• Bruce Ratner, Pythagoras: Everyone knows his famous theorem, but not who discovered it 1000 years before him, Journal of Targeting, Measurement and Analysis for Marketing volume 17, pages229–242, 2009

הערות שוליים

1. Eli Maor, The Pythagorean Theorem: A 4,000-Year History, Princeton University Press, 2007
2. and algebra in ancient civilizations, Chapter 1 van der Waerden B.L., Geometry
3. The mathematical legacy of ancient egypt by Beatrice Lumpkin, page 27
4. משפט פיתגורס בתקופה הבבלית
5. The Indian Sulbasutras
6. Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd
7. ה"יסודות" של אוקלידס כרך 1 משפט 47 עמודים 46–48
8. Steven Strogatz, Einstein’s Boyhood Proof of the Pythagorean Theorem, The New Yorker, ‏November 19, 2015
9. הוכחת אוקלידס מופיעה גם בספרו של הגאון מווילנה, איל משולש, בסעיף ע"ו
10. שכן משולש KAC שווה בשטחו למשולש KAH (בשניהם הגובה של המשולש הוא AH ואחת הצלעות היא AK), ומשולש KAH קל לראות ששטחו שווה לחצי שטח המלבן AKJH
11. On the theorem of pythagoras מאמרו של אדסחר דייקסטרה על משפט פיתגורס
12. L. Hoehn, A Neglected Pythagorean-Like Formula, Mathematical Gazette, 84 (2000), pp. 71-73
13. ה"יסודות" של אוקלידס, כרך שישי, פרק 31
14. The American Mathematical Monthly, Vol. 36, No. 1 (Jan., 1929), pp. 32-34
15. שקילות אקסיומת המקבילים למשפט פיתגורס מתוך האתר cut-the-knot
16. כתבי אפלטון, תרגם מיוונית יוסף ליבס, הוצאת שוקן, 1977, כרך ראשון, עמ' 432–439

ערך מומלץ