From Wikipedia, the free encyclopedia
Os números arábigos[1] ou arábico[2], tamén chamados números indoarábigos, son os símbolos máis empregados para representar números. Chámaselles "arábigos" porque os hispano-árabes de Al-Andalus os introduciron en Europa a través a súa acción cultural, aínda que, en realidade, a súa invención xurdiu na India. O mundo débelle á cultura india o invento transcendental do sistema de numeración posicional, así como o 0, chamado śūnya ou bindu en lingua sánscrita. Porén, os maias tamén coñeceron estes conceptos. Os matemáticos persas da India adoptaron o sistema, de quen o tomaron os árabes. Para o momento en que se comezaron a empregar no norte de África, xa tiñan a súa forma actual e de alí foron adoptados en Europa na Idade Media. O seu uso aumentou en todo o mundo debido á colonización e ao comercio europeos. Unha importante transmisora desta adopción ás linguas europeas foi a lingua castelá, que tamén contribuíu coa adopción de vocábulos matemáticos de influencia árabe como álxebra, algoritmo, cero, cifra, algarismo...[3]

Dado que en occidente existen dúas versións principais coñecidas en función de se cando se usan combinadas co alfabeto latino ou co alifato árabe, é habitual ver usada a expresión números árabes só para o segundo caso (numerais arábigos orientais ou arábigo-índicos). A versión persa ou urdú só se diferencia da segunda nos números 4, 5 e 6.
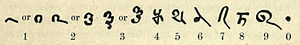

O sistema de numeración arábigo considérase un dos avances máis significativos das matemáticas. A maioría dos historiadores coinciden en afirmar que tivo a súa orixe na India (os árabes refírense a este sistema de numeración como "números indios"), expandiuse polo mundo islámico e de aí, a través de Al-Andalus, ao resto de Europa.
Especúlase que a orixe do sistema posicional con base 10 empregado na India tivese as súas orixes na China. O sistema chinés Hua Ma é tamén posicional e de base 10 e puido servir de inspiración para o sistema que xurdiu na India. Esta hipótese cobra forza polo feito de que entre os séculos V e VIII (período durante o cal se desenvolveu o sistema numérico indio) se produciu unha grande afluencia de peregrinos budistas entre a China e a India. O que é certo é que na época de Bhaskara I (século VII) na India empregábase un sistema de numeración posicional en base 10 con 9 glifos, e coñecíase o concepto do cero, representado por un punto.
Este sistema de numeración chegou a Oriente Medio contra o ano 670. Matemáticos musulmáns do actual Iraq, como Al-Khwarizmi, xa estaban familiarizados coa numeración babilónica, que empregaba o cero entre díxitos distintos de cero (aínda que non tras deses díxitos), así que o novo sistema non tivo un bo recibimento. No século X os matemáticos árabes incluíron no seu sistema de numeración as fraccións. Al-Khwarizmi escribiu o libro coñecido como Algoritmi de numero Indorum ("Sobre os cálculos cos números da India") contra o ano 825 e Al-Kindi escribiu Ketab fi Isti'mal al-'Adad al-Hindi ("O uso dos números da India") en catro volumes. O seu traballo foi moi importante na difusión do sistema da India no Oriente Medio e no Occidente.[4]
Curiosamente, no mundo musulmán soamente os matemáticos empregaban o sistema de numeración arábigo até tempos relativamente recentes. Os científicos usaban o sistema babilónico e os comerciantes os sistemas grego e hebreo.
As primeiras mencións destes numerais na literatura occidental atópanse no Codex Vigilanus do ano 976.[5] A partir de 980 Gerberto de Aurillac, máis tarde papa co nome de Silvestre II, fixo uso do seu oficio papal para difundir o coñecemento do sistema en Europa. Fibonacci, un matemático italiano que estudara en Béjaïa (na actual Alxeria), contribuíu á difusión por Europa do sistema arábigo co seu libro Liber Abaci, publicado en 1202. Entre os primeiros países nos que se recollen áchase Gran Bretaña, onde se teñen escritos como un texto sobre liño na igrexa de Braye de 1448 en Berkshire e outro en Escocia de 1470 na tumba de Eral de Huntly.[6] Na Europa central, o rei de Hungría Ladislau o Póstumo comezou a empregar os números arabigos, téndose rexistro dun documento real de 1456.[7]
Con todo, non foi senón até a invención da imprenta en 1450, cando este sistema de numeración comezou a empregarse de forma xeneralizada en Europa; no século XV xa se utilizaba amplamente.
Os números arábigos substituíron a numeración cirílica en Rusia arredor de 1700, cando foron introducidos polo tsar Pedro I de Rusia.

Os números arábigos foron introducidos na China durante a dinastía Yuan (1271–1368) polo pobo Hui, que era musulmán. A principios do século XVII os xesuítas españois e portugueses introduciron os números arábigos de estilo europeo.[8][9][10]
No Xapón, os números arábigos e o alfabeto latino forman parte do sistema de escritura rōmaji. Así, se un número está escrito con glifos arábigos, no Xapón dirase que "está escrito en rōmaji" en contraposición á numeración xaponesa.
O sistema arábigo representouse (e represéntase) utilizando varios conxuntos de glifos diferentes, que puideron evolucionar dos números brahmi ou ben desenvolvérense de xeito independente. Estes símbolos empregados para representar o sistema diferencious dende a Idade Media en variantes tipográficas:
| Europeo | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Arábigo-índico | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Arábigo-índico oriental (persa e urdú) |
۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ |
| Devanágari (hindi) |
० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ |
| Támil | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ |
A evolución dos numerais en Europa amósase na táboa creada polo francés Jean-Étienne Montucla na súa obra Histoire de la Mathematique, publicada en 1757:
A pesar da evidencia, persisten algunhas explicacións folclóricas da orixe dos numerais arábigos modernos. Estas hipóteses continúan propagándose debido aos seus argumentos aparentemente ben construídos, pero están baseadas nas especulacións de individuos que, a pesar de estar intrigados de maneira xenuína polo tema, carecían do coñecemento dos feitos arqueolóxicos relevantes ou vivían nunha época anterior á que volveron ser descubertos. Un destes mitos populares propón que as formas orixinais dos símbolos indicaban o seu valor a través da cantidade de ángulos que contiñan.
Como se pode ver na imaxe o cero non ten ángulos e cada un dos símbolos restantes teñen o número de ángulos correspondentes ao número representado.[11][12]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.