Unuforma pluredro

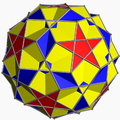
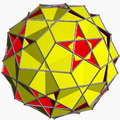
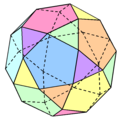
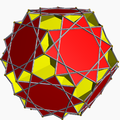
Unuforma pluredro estas unuforma hiperpluredro, 3-dimensia pluredro kiu havas regulaj plurlateroj kiel edroj kaj estas vertico-transitiva. Ĉiuj ĝiaj verticoj estas kongruaj, kaj la pluredro havas altan gradon de reflekta kaj turna simetrio.

Unuformaj pluredroj povas esti regula, kvazaŭregula aŭ duonregula. La edroj kaj verticoj ne nepre esta konveksaj, inter unuformaj pluredroj estas ankaŭ stelaj pluredroj.

Malinkluzivante la malfiniajn arojn estas 75 unuformaj pluredroj (aŭ 76 se al lateroj estas permesite koincidi).

La kategorioj inkluzivas:

• Malfiniaj aroj de unuformaj prismoj kaj kontraŭprismoj (inkluzivanta stelajn formojn)
• 5 platonaj solidoj - regulaj konveksaj pluredroj
• 4 pluredroj de Keplero-Poinsot - regulaj nekonveksaj pluredroj
• 13 arĥimedaj solidoj - kvazaŭregula kaj duonregulaj konveksaj pluredroj
• 14 nekonveksaj pluredroj kun konveksaj edroj
• 39 nekonveksaj pluredroj kun nekonveksaj edroj
• 1 pluredro trovita de John Skilling ĉe kiu paroj de lateroj koincidas.

Ili povas ankaŭ esti grupita per ilia geometria simetria grupo, kio estas farita pli sube.

Historio

• La platonaj solidoj estas konataj ekde la klasikaj grekoj kaj estis studitaj de Platono, Theaetetus kaj Eŭklido.
• Keplero (1571-1630) estis la unua kiu publikigis la plenan liston de arĥimedaj solidoj post kiam la originala laboro de Arkimedo estis perdita.
• Keplero (1619) esploris du de la regulajn pluredroj de Keplero-Poinsot kaj Louita Poinsot (1809) esplorita la aliajn du.
• De la ceteraj 37 estis trovitaj de Badoureau (1881). Edmund Hess (1878) esploris 2 pliajn kaj Pitsch (1881) sendepende esploris 18-n, el ili ne ĉiuj antaŭe esplorita.
• Harold Scott MacDonald Coxeter esploris la ceterajn dek du en kunlaboro kun J.C.P. Miller (1930-1932) sed ne publikigis la laboron. M.S. kaj H.C. Longuet-Higgins sendepende esploris 11-n el ĉi tiuj.
• En 1954 H.S.M. Coxeter, M.S. Longuet-Higgins, J.C.P. Miller publikigis la liston de unuformaj pluredroj.
• En 1970 S. P. Sopov pruvis ilia konjekton ke la listo estis plena.
• En 1974, Magnus Wenninger publikigis lian libron, Pluredraj modeloj, kiu estas la unua publikigita listo de ĉiuj 75 neprismaj unuformaj pluredroj, kun multaj antaŭe nepublikigitaj nomoj donitaj al ili de Norman Johnson.
• En 1975, John Skilling sendepende pruvis la plenecon, kaj montris ke se la difino de unuforma pluredro estas malstreĉiĝita al permesi al randoj koincidi tiam estas nur unu superflua ebleco.
• En 1993, Zvi Har'El produktis plenan komputilan konstruadon de la unuformaj pluredroj kaj dualaj tra ilia kalejdoskopa konstrua programo nomata kiel Kaleido, kaj resumis en papero Unuforma solvaĵo por unuformaj pluredroj., donante al ili numerojn 1-80.
• Ankaŭ en 1993, R. Mäder aplikis solvaĵon de ĉi tiu Kaleido al Mathematica kun malmulte malsama indeksanta sistemo.

Indeksado

Estas kvar gravaj publikaĵoj indeksantaj la pluredrojn. Por distingi ilin, al la indeksoj estas aldonataj malsamaj literoj, C por la Coxeter 1954, W por la Wenninger 1974 , K por la Kaleido 1993, kaj U por la 1993 Maeder, kiu estas (mult)amplekse reproduktita aliloke. Nun U estas la plej kutima indeksado de la pluredroj.

1. [C] 1954: Ĉi tiu papero listigas la unuformaj pluredroj per nombroj 15-92. 15-32 estas por la konveksaj, 33-35 por 3 malfiniaj prismaj aroj, kaj 36-92 por la nekonveksaj.
2. [W] 1974: nombris ilin 1-119: 1-5 por la platonaj solidoj, 6-18 por la arĥimedaj solidoj, 19-66 por steligitaj formoj inkluzivante la 4 regulaj nekonveksaj pluredroj (sed plejparto de la steligitaj pluredroj estas neunuformaj), kaj 67-119 por la nekonveksaj unuformaj pluredroj. (La plenan liston de W_i rigardu en listo de pluredroj de Wenninger)
3. [K] 1993 Kaleido: La 80 nombroj donitaj estis grupita per simetrio: 1-5 kiel prezentantoj por la malfiniaj familioj de prismaj formoj kun duedra simetrio, 6-9 kun kvaredra simetrio, 10-26 kun Okedra simetrio, 46-80 kun dudekedra simetrio.
4. [U] 1993 Mathematica: Ĉi tiu listante sekvis la nombradon de Kaleido, sed movis la 5 prismajn formojn al fino de la listo, kaj la neprismaj havas numerojn 1-75.

Konveksaj formoj kaj fundamentaj situoj de verticoj

La konveksaj unuformaj pluredroj povas esti nomitaj per operacioj de konstruo de Wythoff sur la gepatra formo.

Ĉiu de ĉi tiuj konveksaj formoj difinas aron de verticoj kiuj povas esti uzataj ankaŭ por la nekonveksaj formoj, listigitaj en la sekva sekcio.

	Gepatra	Senpintigita	Rektigita	Dutranĉita (senpintigita dualo)	Durektigita (duala)	Laterotranĉita	Entutotranĉita	Riproĉa
Etendita simbolo de Schläfli	${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}q,p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}}$	${\displaystyle r{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}p\\q\end{Bmatrix}}}$
	t0{p,q}	t0,1{p,q}	t1{p,q}	t1,2{p,q}	t2{p,q}	t0,2{p,q}	t0,1,2{p,q}	s{p,q}
Simbolo de Wythoff p-q-2	q | p 2	2 q | p	2 | p q	2 p | q	p | q 2	p q | 2	p q 2 |	| p q 2
Figuro de Coxeter-Dynkin (variadoj)
	(o)-p-o-q-o	(o)-p-(o)-q-o	o-p-(o)-q-o	o-p-(o)-q-(o)	o-p-o-q-(o)	(o)-p-o-q-(o)	(o)-p-(o)-q-(o)	( )-p-( )-q-( )
	xPoQo	xPxQo	oPxQo	oPxQx	oPoQx	xPoQx	xPxQx	sPsQs
	[p,q]:001	[p,q]:011	[p,q]:010	[p,q]:110	[p,q]:100	[p,q]:101	[p,q]:111	[p,q]:111s
Vertica konfiguro	pq	(q.2p.2p)	(p.q.p.q)	(p.2q.2q)	qp	(p.4.q.4)	(4.2p.2q)	(3.3.p.3.q)
Kvaredra 3-3-2	{3,3}	(3.6.6)	(3.3.3.3)	(3.6.6)	{3,3}	(3.4.3.4)	(4.6.6)	(3.3.3.3.3)
Okedra 4-3-2	{4,3}	(3.8.8)	(3.4.3.4)	(4.6.6)	{3,4}	(3.4.4.4)	(4.6.8)	(3.3.3.3.4)
Dudekedra 5-3-2	{5,3}	(3.10.10)	(3.5.3.5)	(5.6.6)	{3,5}	(3.4.5.4)	(4.6.10)	(3.3.3.3.5)
Duedra p-2-2 Ekzemple p=5	{5,2}	2.10.10	2.5.2.5	4.4.5	{2,5}	2.4.5.4	4.4.10	3.3.3.5

Difino de operacioj

Operacio	Etendita simbolo de Schläfli		Figuro de Coxeter-Dynkin	Priskribo
Gepatro	t0{p,q}	${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$		Ĉiu regula pluredro aŭ kahelaro
Rektigita	t1{p,q}	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$		La randoj estas plene-senpintigitaj en solajn punktojn. La pluredro nun havas la kombinitajn edrojn de la gepatro kaj la dualo.
Durektigita ankaŭ Duala	t2{p,q}	${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}}$		La durektigita (duala) estas plua tranĉo tiel ke la originalaj edroj estas reduktitaj al punktoj. Novaj edroj estas formitaj sub ĉiu gepatra vertico. La nombro de randoj estas neŝanĝita kaj estas turnita je 90 gradoj. La duala de la regula pluredro {p, q} estas ankaŭ regula pluredro {q, p}.
Senpintigita	t0,1{p,q}	${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}}$		Ĉiu originala vertico estas dehakita, kun novaj edroj enspacas la truojn. Tranĉo havas gradon de libereco, kiu havas unu solvaĵo kiu kreas unuforman senpintigitan pluredron. La pluredro havas ĝiaj originalaj edroj kun duobligita kvanto de lateroj en ĉiu el la edroj, kaj enhavas la edrojn de la duala.
Dutranĉita	t1,2{p,q}	${\displaystyle t{\begin{Bmatrix}q,p\end{Bmatrix}}}$		Sama kiel senpintigita duala.
Laterotranĉita (aŭ rombigita) (ankaŭ elvolvita)	t0,2{p,q}	${\displaystyle r{\begin{Bmatrix}p\\q\end{Bmatrix}}}$		Aldone al vertica tranĉo, ĉiu originala rando estas bevelita kun novaj rektangulaj edroj aperantaj en ĝia loko, kaj ankaŭ la originalaj verticoj estas senpintigitaj. Unuforma laterotranĉo estas duonvoje inter la gepatra kaj la duala formoj.
Entutotranĉita (aŭ rombotranĉita)	t0,1,2{p,q}	${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}}$		La tranĉaj operacioj estas aplikitaj por krei entutotranĉitan formon kiu havas la gepatraj edroj kun duobligita kvanto de lateroj en ĉiu el la edroj, kaj kvadratojn tie kie la originalaj randoj ekzistis.
Riproĉa	s{p,q}	${\displaystyle s{\begin{Bmatrix}p\\q\end{Bmatrix}}}$		La riproĉa prenas la entutotranĉitan formon kaj rektigas alternajn verticojn. Ĉi tiu operacio estas nur ebla por pluredroj kun ĉiuj edroj kun paraj kvantoj de verticoj. Ĉiuj originalaj edroj havas nur duonon de verticoj, kaj la kvadratoj degeneras en laterojn. Ĉar la entutotranĉita havas 3 edrojn/vertico, novaj trianguloj estas formitaj. Kutime poste necesas malmulte misformigi la pluredron por ke ĝi denove estu unuforma. La ebleco de la lasta variado dependas de la grado de libereco.

Nekonveksaj formoj listitaj laŭ geometriaj simetriaj grupoj kaj situoj de verticoj

Ĉiuj unuformaj pluredroj estas listita pli sube laŭ iliaj geometriaj simetriaj grupoj kaj subgrupitaj laŭ iliaj situoj de verticoj.

Regulaj pluredroj estas markitaj per iliaj simboloj de Schläfli. Aliaj neregulaj unuformaj pluredroj estas listitaj kun iliaj verticaj konfiguroj aŭ ilia unuformaj pluredraj indeksoj U(1-80).

Noto: por nekonveksaj formoj pli sube estas aldonita komento neunuforma se la konveksa koverto de la situo de verticoj havas sama topologio kiel unu el unuformaj pluredroj, sed havas neregulajn edrojn. Ekzemple neunuforma laterotranĉita formo povas havi nekvadratajn ortangulojn kiel edroj.

Kvaredra simetrio

Estas 2 konveksaj unuformaj pluredroj, la kvaredro kaj senpintigita kvaredro, kaj unu nekonveksa formo, la kvar-duon-sesedro kiu havi kvaredran simetrion. La kvaredro estas mem duala.

Aldone la okedro, senpintigita okedro, kubokedro, kaj dudekedro havas kvaredran simetrion kaj ankaŭ pli altan simetrion. Ili estas aldonitaj por pleneco pli sube, kvankam iliaj nekonveksaj formoj kun okedra simetrio ne estas inkluzivitaj ĉi tie.

Vertica grupo	Konveksa	Nekonveksa
(Kvaredra)	{3,3}
Senpintigita (*)	(3.6.6)
Rektigita (*)	{3,4}	(4.3/2.4.3)
Laterotranĉita (*)	(3.4.3.4)
Entutotranĉita (*)	(4.6.6)
Riproĉa (*)	{3,5}

Okedra simetrio

Estas 8 konveksa formoj kaj 10 nekonveksaj formoj kun okedra simetrio.

Vertica grupo	Konveksa	Nekonveksa
(Okedra)	{3,4}
Senpintigis (*)	(4.6.6)
Rektigita (*)	(3.4.3.4)	(6.4/3.6.4)	(6.3/2.6.3)
Senpintigita duala (*)	(3.8.8)	(4.8/3.4/3.8/5)	(8/3.3.8/3.4)	(4.3/2.4.4)
Duala (*)	{4,3}
Laterotranĉita (*)	(3.4.4.4)	(4.8.4/3.8)	(8.3/2.8.4)	(8/3.8/3.3)
Entutotranĉita (*)	(4.6.8)
Neunuforma entutotranĉita (*)	(4.6.8)	(8/3.4.6)	(8/3.6.8)
Riproĉa (*)	(3.3.3.3.4)

Dudekedra simetrio

Estas 8 konveksa formoj kaj 46 nekonveksaj formoj kun dudekedra simetrio (aŭ 47 nekonveksa formoj se figuro de Skilling estas inkluzivita). Iu el la nekonveksa riproĉaj formoj havas neunuforman turnecan simetrion, kaj iu estas memspegulsimetriaj.

Vertica grupo	Konveksa	Nekonveksa
(Dudekedra)	{3,5}	{5/2,5}	{5,5/2}	{3,5/2}
Senpintigita (*)	(5.6.6)
Neunuforma senpintigita (*)	(5.6.6)	U37	U61	U67	U73	U38	U44	U56	U32
Rektigita (*)	(3.5.3.5)	U49	U51	U54	U70	U71	U36	U62	U65
Senpintigita duala (*)	(3.10.10)	U42	U48	U63
Neunuforma senpintigita duala (*)	(3.10.10)	U72
Duala (*)	{5,3}	{5/2,3}	U30	U41	U47
Laterotranĉita (*)	(3.4.5.4)	U33	U39	U58
Neunuforma laterotranĉita (*)	(3.4.5.4)	U31	U43	U50	U66	U55	U75	U64
Entutotranĉita (*)	(4.6.10)
Neunuforma entutotranĉita (*)	(4.6.10)	U68	U59	U45
Riproĉa (*)	(3.3.3.3.5)
Neunuforma riproĉa (*)	(3.3.3.3.5)	U40	U46	U57	U69	U60	U74

Duedra simetrio

Pli detalaj informoj troveblas en artikolo Prisma unuforma pluredro.

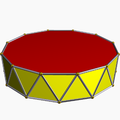
Unuformaj pluredroj kun duedra simetrio estadas de jenaj specoj:

Konveksa prismo	Konveksa kontraŭprismo	Stela prismo	Stela kontraŭprismo (kun konveksa vertica figuro)	Stela krucigita kontraŭprismo (kun nekonveksa vertica figuro)
U76	U77	U78	U79	U80

Ekzistas malfinie multaj unuformaj pluredroj de ĉiu el la 5 specoj, diferenciĝantaj per kvanto de verticoj aŭ per maniero de konekseco de la steloj.

Figuro de Skilling

Unu plua nekonveksa pluredro estas la granda duriproĉa durombo-dekduedro, ankaŭ sciata kiel figuro de Skilling, kiu estas vertico-unuforma, sed havas parojn de lateroj kiu koincidas en spaco tiel ke kvar edroj kuniĝas je ĉi tiuj lateroj.

Ĝi estas iam sed ne ĉiam enkalkulita kiel unuforma pluredro. Ĝi havas I_h simetrion.

Vidu ankaŭ

• Pluredro
  • Regula pluredro
  • Kvazaŭregula pluredro
  • Duonregula pluredro
• Listo de regulaj hiperpluredroj
• Listo de unuformaj pluredroj
• Listo de pluredroj de Wenninger
• Pluredra modelo
• Listo de unuformaj pluredroj laŭ vertica figuro
• Listo de unuformaj pluredroj laŭ simbolo de Wythoff
• Uniforma pluredra kombinaĵo
• Unuforma kahelaro
• Unuforma hiperpluredro

Referencoj

• Brückner, M. Vielecke und vielflache. Theorie und geschichte.. Leipzig, Germanio: Teubner, 1900.
• H.S.M. Coxeter, M.S. Longuet-Higgins, J.C.P. Miller, Unuformaj pluredroj, Phil. Trans. 1954, 246 A, 401-50
• S. P. Sopov Pruvo de la pleneco de la listo de rudimentaj homogenaj pluredroj. Ukrain. Geometr. Sb. Ne. 8, (1970), 139-156
• Wenninger, Magnus. (1974) Polyhedron Models - Pluredraj modeloj. Cambridge University Press. ISBN 0-521-09859-9.
• John Skilling, La plenumi aro de unuformaj pluredroj., Filoj de Aleksandrio. Trans. Roy. Soc. Londono Ser. 278 (1975), 111-135
• Har'El, Z. Unuforma solvaĵo por unuformaj pluredroj., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El Arkivigite je 2009-07-27 per la retarkivo Wayback Machine Arkivigite je 2009-07-15 per la retarkivo Wayback Machine, programaro Kaleido Arkivigite je 2011-05-20 per la retarkivo Wayback Machine, Bildoj Arkivigite je 2011-05-20 per la retarkivo Wayback Machine, dualaj bildoj Arkivigite je 2011-05-20 per la retarkivo Wayback Machine
• Mäder, R. E. Unuformaj pluredroj. Mathematica J. 3, 48-57, 1993.

Eksteraj ligiloj

• Kategorio Unuforma pluredro en la Vikimedia Komunejo (Multrimedaj datumoj)

• Eric W. Weisstein, Unuforma Pluredro en MathWorld.
• Unuforma solvaĵo por unuformaj pluredroj Arkivigite je 2009-07-15 per la retarkivo Wayback Machine
• La unuformaj pluredroj
• Virtualaj pluredroj
• Stella: Pluredra Navigilo Arkivigite je 2007-11-12 per la retarkivo Wayback Machine - Programaro por generi kaj printi retojn por ĉiuj unuformaj pluredroj
• Paperaj modeloj:
  • Unuformaj/dualaj pluredroj Arkivigite je 2007-10-12 per la retarkivo Wayback Machine
  • Paperaj modeloj de unuformaj kaj aliaj pluredroj