Loading AI tools
来自维基百科，自由的百科全书
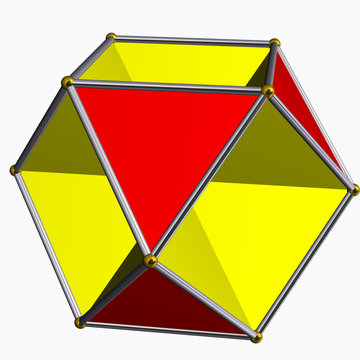
在幾何學中，八面半八面體是一種非凸多面體，屬於星形多面體及均勻多面體[1]，也可以歸類在非凸均勻多面體，其索引為U3。八面半八面體由8個正三角形和4個正六邊形組成，且每個頂點對應的角皆相等，因此也可以被歸類為擬正多面體[2]，然而由於這個立體同時具備半多面體的特性，因此被部分學者分成一類新的立體，即擬正半多面體（Versi-Regular Polyhedra），這類立體共有九個，最早在1881年由亞伯特·巴杜羅（Albert Badoureau）發現並描述[3]。特別地，這個立體的邊長與外接球半徑相等[4]。八面半八面體可以與星形八面體共同堆砌填滿空間，因此曾應用於建築結構中。[5]
八面半八面體共有12個面、24條邊和12個頂點[6][7]，是一種十二面體，每個頂點都是2個正三角形和2個六邊形的公共頂點。[6]
八面半八面體是唯一可定向且歐拉示性數為零的半多面體，[8]這意味著其具有拓撲環面的性質。[9]
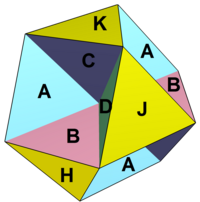 八面半八面體 |
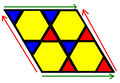
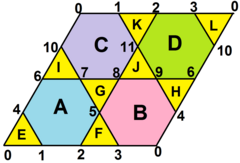 八面半八面體在拓樸上的展開圖可以排佈為分割成8個正三角形和4個正六邊形的菱形。所有頂點的角虧為零 |
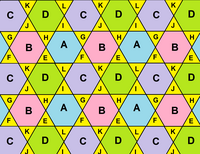 這個展開圖是截半六邊形鑲嵌的一部份，在威佐夫符號中計為3 3 | 3、考克斯特-狄肯記號計為   
|
八面半八面體僅有一種二面角，為三角形和六邊形的棱之交角，其值為三分之一的反餘弦值[10][11]：
其值約為70度31分43.6秒
由於其凸包為截半立方體，因此其12頂點會與截半立方體相同，為(0, ±1, ±1),(±1, 0, ±1),(±1, ±1, 0)，若邊長為a，則座標要縮放倍。[12]
八面半八面體具有抽象多胞形半三角形面和互相相交的六邊形面，但若去除相交的面作為一個簡單多面體，則其可以視為由32個正三角形組成的凹多面體[13][14]。這種多面體共有32個面、48條邊和13個頂點，其結構與四角化截半立方體拓樸同構，不過四角化截半立方體有18個頂點而這種多面體僅有13個頂點是因為有6個頂點在中心共用。另一方面，這個立體也可以視為由8個正四面體組合而成。[15]:103
八面半八面體的對偶多面體是八面半無窮星形八面體。其外觀與立方半無窮星形八面體相同[16]。
從定義上來看，對偶多面體的面會與原始立體的頂點圖相同，同時頂點周圍之面的排列方式會和原始立體的面之邊相同，也就是說對偶多面體的頂點圖為原始立體的面[17]。由於八面半無窮星形八面體是八面半八面體的對偶多面體，而八面半八面體的12個頂點皆為4個面的公共頂點，因此八面半無窮星形八面體的面理應具有12個面，每個面由4個邊組成[7]。然而八面半八面體有部分面幾何中心落在整個立體的幾何中心上，因此其對偶多面體的頂點會落在無窮遠處，即無窮實射影平面上的點。[18]一般來說，這樣的立體無法被具象化[7]。為了具像化這種立體，溫尼爾在著作《對偶模型》中將其描述為由無限高的柱體組合構成的立體，在這樣的視覺化方式下，八面半八面體外觀為由4個無限高的六角柱構成的立體[18]。
八面半八面體可透過截去皮特里立方體的所有頂點來構造，也就是說，八面半八面體可以視為截半的皮特里立方體。[20][21]
中心八面半八面體數是一種排列成八面半八面體的有形數。第n個中心八面半八面體數可以表示為[23]。由於八面半八面體數與截半立方體共用相同的頂點排列方式，因此數列前兩項與中心截半立方體數（OEIS數列A005902）相同，第三項開始少去了八面半八面體數相對於截半立方體缺少的6個四角錐[23]
前幾個中心八面半八面體數為：
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
